基于学习路径分析的“有余数的除法”单元整体教学

邵蓓瑜 章勤琼 麻永侃

【摘 要】竖式记录每一步计算的过程。要理解其算理，就要在教学中做好情境意义、操作过程与竖式记录的关联。“有余数的除法”单元的核心目标有两个：（1）理解有余数的除法的含义以及余数与除数的关系；（2）理解除法竖式的合理性并掌握除法竖式。从有余数的除法开始学习除法竖式，能让学生更好地理解除法竖式的合理性。同时，学习除法竖式的过程，又能帮助学生更好地理解除法含义。

【关键词】学习路径；单元整体教学；有余数的除法；竖式

除法的本质是不断地对不同单位的总数进行平均分的过程，分了之后对剩余的进行转化，与下面的单位进行合并，然后再重复这样的过程。［1］因此，除法竖式需要记录每次平均分过程的“分什么？要分多少份（每份分多少）？每份分多少（能分多少份）？分了多少？还余多少？”五个步骤。如果有不同单位的多次均分，还需要处理“余下的怎么办”的问题，并继续记录这一过程。这样的除法竖式不仅是在记录计算的过程，还与整个算理理解和思考过程对应。［2］在“有余数的除法”单元教学中，教师容易忽视竖式记录的关联性，即没有做好情境意义、计算过程与竖式记录的关联，导致学生停留在浅层次的程序化记忆中，失去了理解除法竖式的合理性与深化理解除法意义的机会。在教学时，该如何帮助学生进行有意义的竖式记录，进而理解除法竖式的合理性，明晰除法意义呢？本文通过基于学习路径的“有余数的除法”单元整体设计来进行说明。

一、理解学习目标

（一）单元目标概述

1.人教版教材单元目标

（1）通过操作、观察、对比等活动，使学生发现日常生活中在分物时存在着分不完有剩余的情况，借此理解余数及有余数的除法的含义，初步培养学生全面思考问题的意识。（2）通过操作、计算、比较等活动，让学生经历除法竖式（含表内除法的竖式）的书写过程，理解竖式中每个数所表示的意思，初步培养学生的观察、分析能力以及恰当地进行数学表达的能力。（3）使学生初步掌握试商的基本方法，并能较熟练地进行有余数的除法的口算和笔算，培养学生的运算能力。（4）使学生初步学会用有余数的除法解决生活中的简单问题，初步感受数学与生活的联系，继续掌握解决问题的基本思路和基本方法。［3］

2.北师大版教材单元目标

（1）能在教师的指导下，从日常生活中提出简单的除法问题；在解决实际问题和对结果的实际意义进行解释的过程中，进一步体会除法的意义，感受除法与生活的密切联系。（2）能读懂情境图中蕴含的信息，初步学习画图、列表等多样化的解决问题的策略，知道同一个问题可以有不同的解决方法，并运用有余数的除法解决简单的实际问题。（3）认识余数并经历探索余数和除数关系的过程；掌握商是一位数的除法竖式的书写格式，了解除法竖式各部分的意思；经历有余数除法的试商过程，进一步体会余数一定要比除数小。（4）乐于参加数学活动，初步形成对数学的好奇心和探索欲望。［4］

两个版本教材的单元目标都包含三个板块的内容和要求：（1）理解有余数的除法的含义及余数与除数的关系；（2）理解除法竖式的合理性并掌握除法竖式；（3）运用有余数的除法解决问题。

（二）确定核心目标

根据单元目标可知，理解有余数的除法的含义是学习除法竖式的基础，同时，除法竖式的学习又能帮助学生进一步理解有余数的除法的含义，促进学生用有余数的除法解决问题。因此，本单元的核心目标是：（1）理解有余数的除法的含义及余数与除数的关系；（2）理解除法竖式的合理性并掌握除法竖式。

（三）核心目标具体化

确定上述核心目标后，还需根据运算意义以及竖式记录过程，分析核心目标的内涵，形成具体的表现性目标。

1.理解有余數的除法的含义

能理解平均分后有剩余的情境；能用自己的方式表征平均分的过程并能结合情境作解释；能在理解、比较不同方法的基础上，用有余数的除法算式表征情境，并理解除法算式各部分的含义；理解余数与除数的关系。

2.理解除法竖式的合理性并掌握除法竖式

能结合情境意义和平均分的过程，用除法竖式进行记录；能结合情境，借用除法横式对除法竖式进行解释、筛选；能理解除法竖式的合理性，理解除法竖式各部分的含义。

根据核心目标可知，明晰有余数的除法的含义能帮助学生理解除法竖式记录的必要性，而除法竖式记录过程又能促进学生对算理的理解。教学时应建立情境意义、计算过程、竖式记录三者之间的联系，使除法竖式的学习成为理解算理、掌握算法的过程，凸显竖式的作用与价值。

二、确定学习起点

根据具体化目标，学生对平均分的过程和除法含义的理解是本单元的学习基础。因此，笔者设计了两道表现性评价的题目，对二年级41名学生进行测试，并根据SOLO分类理论对学生的答题情况进行水平分层的分析。

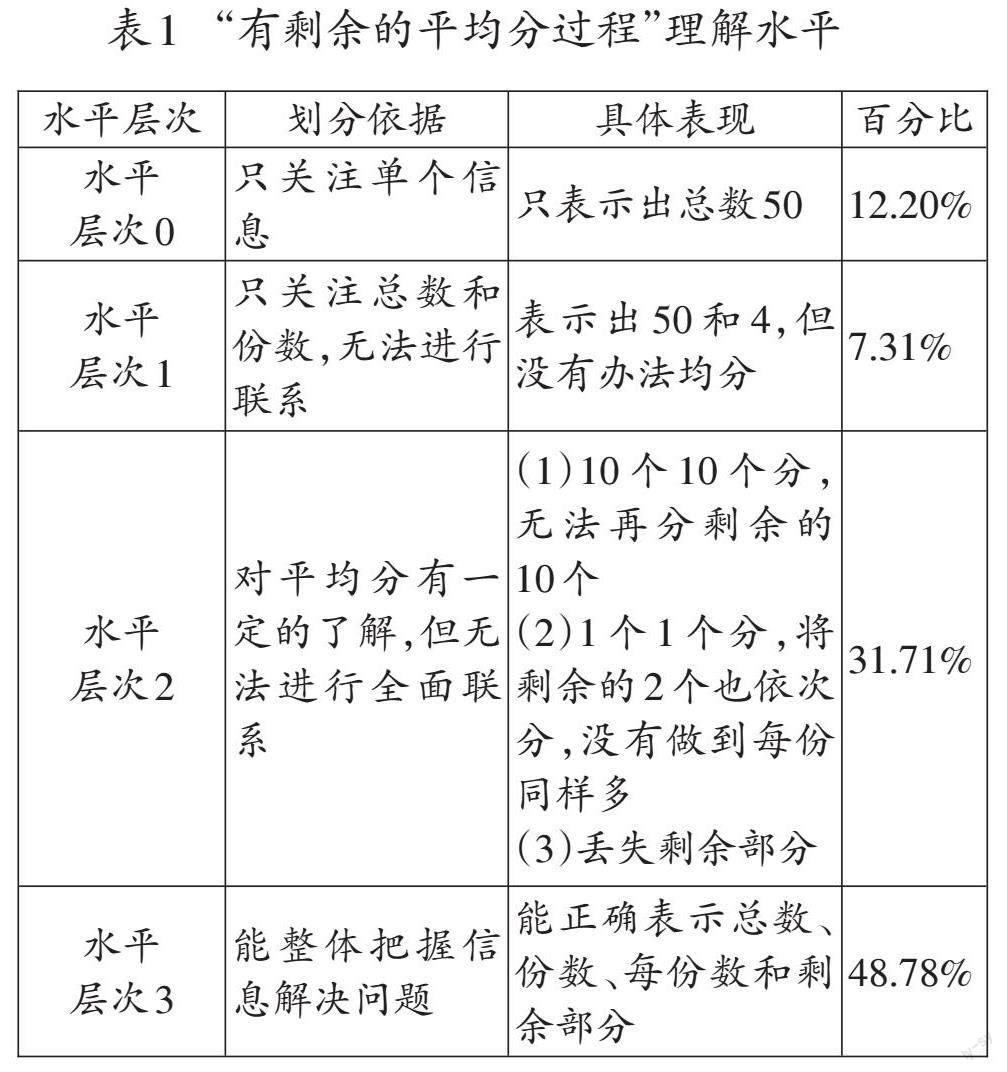
测试题1：将50颗糖果平均分给4个人，你是怎么分的？请你用图或文字等形式把分的过程清楚地记录下来。

本题考查学生对“有剩余的平均分过程”的理解情况。根据学生的表现，其理解水平可以划分为4个水平层次，测查结果如表1所示。

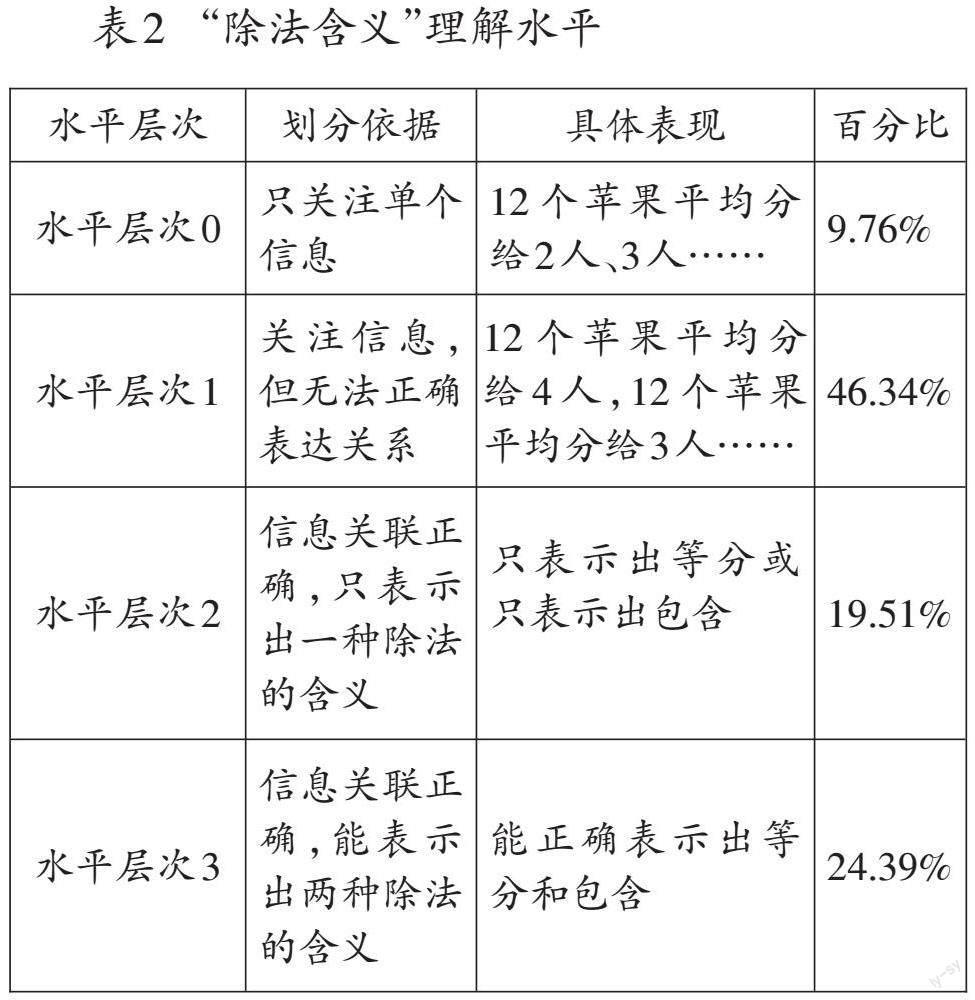
测试题2：算式“12÷4=3”中的12表示12个苹果，这个算式可以用来解决什么问题？请写出你觉得可能解决的问题。

本题是为了考查学生对除法的两种含义（等分和包含）的理解情况。学生的表现可分为4个水平层次，测查结果如表2所示。

由这两道测试题可以看出，约20%的学生（表1中水平0和水平1）对有余数的除法均分过程的理解存在困难，因此，在教学中需要适当进行提示，以明晰学生的思维过程；约56%的学生（表2中水平0和水平1）对除法两种含义的理解不足，因此在教学时要建立情境意义和运算过程的对应关系，促进学生对除法含义的理解。

三、分析学习路径

学生在第一次学习除法竖式时，不仅需要知道竖式怎么列，还要在理解算理的情况下，将情境意义、计算过程以及竖式记录进行关联，理解竖式为什么这么列。通过有余数的除法来学习除法竖式，能让学生更好地理解除法竖式的合理性。由此，笔者确定了本单元的学习路径，并在学生运用有余数的除法解决简单的实际问题前，根据核心目标的具体表现设计了相应的教学任务。

（一）理解有余数的除法的含义

任务一，理解“有剩余的平均分过程”的情境。例如，通过操作活动“用12根小棒摆三角形，结果怎样？用13根小棒摆三角形，结果怎样？”直观理解算理。任务二，能用自己的方式表征平均分的过程并能结合情境作解释。例如，对于用13根小棒摆三角形，学生可能会列出不同的算式：13-3-3-3-3=1（个）、3×4+1=13（个）、13÷3=4（个）……1（根）。教师引导学生根据情境意义和平均分的过程解释不同算式的含义。任务三，根据操作过程来比较不同的表征方式，明确有余数的除法算式可用于表示 “分什么？要分多少份（每份分多少）？每份分多少（能分多少份）？分了多少？还余多少？”五个步骤，理解有余数的除法的内涵，联系平均分的过程理解横式中各部分的含义。任务四，理解除数与余数的关系。首先，让学生理解情境的意义，用13根小棒搭正方形，并用除法算式表示。其次，让学生用除法算式直接表示用14根、15根、16根小棒搭正方形的情况，并通过比较学生的易混点，如16÷4=3（个）……4（根）和16÷4=4（个），引导学生根据情境意义和分的过程进行数学说理，体会除数与余数的关系。再次，让学生用除法算式表示17根、18根、19根、20根小棒搭正方形的情况，检查学生的掌握情况。最后，组织学生观察、比较、分析“用13～16根”和“用17～20根”小棒搭正方形的两组除法算式的相同点和不同点，引导学生发现余数和除数的关系，感受除法算式中被除数、除数、商和余数的变化规律。

以上四个任务分为两个课时，其中任务一、任务二、任务三为一课时，主要结合操作过程帮助学生直观理解算理，再用不同的算式引导学生认识有余数的除法，理解有余数的除法的含义。任务四为一课时，主要结合情境，让学生通过操作活动和除法算式之间的规律，理解余数与除数的关系。

（二）理解除法竖式的合理性并掌握除法竖式

任务一，有13根小棒，每4根分1组，操作后列出算式，并用竖式进行记录。任务二，结合情境和操作过程，对列出的竖式的合理性进行解释。任务三，关联情境意义、计算过程与竖式记录，理解竖式记录的合理性，理解竖式各部分的含义。

四、核心课时任务设计

计算教学要强调算理和算法之间的关联。以“除法竖式”为例，要理解除法竖式记录的合理性，就要在理解算理的基础之上，有效关联情境意义、计算过程和竖式记录。具体教学任务如下。

首先，教师出示任务：“有13根小棒，每4根分1组，结果怎样？”让学生画一画，并写出除法算式。在这个任务中，教师需要借助情境，帮助学生直观地理解平均分的过程，并将分的过程与除法横式建立联系，为学生能够根据情境和除法横式写出不同的除法竖式做铺垫。

其次，结合情境意义，让学生尝试用竖式记录平均分的过程，并鼓励学生写出不同形式的除法竖式。再引导学生结合平均分的过程及除法横式的含义，对写出的除法竖式进行筛选和排除。例如，学生可能会写出如图1的三种竖式。教师要引导学生结合前面平均分的过程，全面观察除法竖式的记录过程，从而发现方法（1）只记录了“分了3组”，而缺少了“还余1根”，导致记录的过程不完整。再分析方法（2）和方法（3），寻找竖式记录的五个步骤：“分13根，每份4根，分3份，分了12根，还余1根。”辨析方法（2）中是否记录下了“分了12根”的内容，从而理解“分了12根”是思维过程中必不可少的部分。之后，对比方法（2）和方法（3），理解把“分了12根”记录下来，才能与之前分的过程真正对应起来。学生经历这样的对比和分析过程，才能理解除法竖式记录的合理性，从而更好地理解除法的运算过程。

最后，關联情境意义、计算过程和竖式记录，让学生理解除法竖式各部分的含义。通过“有余数的除法”的教学，在学生充分理解了除法竖式的合理性之后，再让他们尝试解决没有余数的除法的问题，并用竖式记录计算过程，能帮助学生直观地理解算理，将计算过程和竖式记录进行对应，理解除法竖式各部分的实际意义。

参考文献：

［1］ 章勤琼，唐娟.为什么除法竖式不一样：兼谈竖式的记录功能及不同形式［J］.教学月刊·小学版（数学），2019（10）：56-59.

［2］章勤琼，杜依铭. 运算教学中如何做到“法理兼顾”：略谈运算教学的三个要点［J］. 福建教育，2022 （10）：28-31.

［3］人民教育出版社课程教材研究所小学数学课程教材研究开发中心. 义务教育教科书教师教学用书：数学二年级下册［M］.北京：人民教育出版社，2016：143.

［4］刘坚，孔企平，张丹.义务教育教科书数学教师教学用书：二年级下册［M］.北京：北京师范大学出版社，2013：2.

（1.浙江省温州市永嘉县实验小学 2.福建师范大学教育学院）