异形孔在膨胀荷载作用下的定向致裂机制

苏永华，沈嘉铖，肖俊杰，尹文杰

（湖南大学 土木工程学院，湖南 长沙 410082）

城区深大基坑的挖掘通常紧邻重要构筑物和设施，这意味着其施工场地狭窄、环境条件差、安全要求苛刻.除此之外，经常会遇到工程力学属性独特的软岩地层［1-2］.对此类基坑的挖掘，机械挖掘和传统的钻爆法均存在难以克服的局限性.机械挖掘对于具有相当厚度的岩层而言，效率极低.钻爆法在施工作业时产生大量烟尘和噪声，严重污染环境，并且会在挖掘边界外围岩中造成相当大规模的强烈扰动区，对地表既有建筑物的基础或设施造成灾难性的危害［3］.

破碎剂膨胀静力裂岩是依靠灌装在岩石中孔洞里的破碎剂发生水化反应导致体积膨胀而缓慢地产生拟静态膨胀荷载致裂岩石的一种技术手段.破碎剂不产生有毒有害气体，对围岩的扰动范围微小、扰动程度轻微［4］.现有的研究表明，静态膨胀剂在环境温度为34 ℃、含水率为30%时产生的膨胀压力最大［5］.此外，钻孔直径也会影响膨胀剂的膨胀过程.对于室内模拟试验而言，钻孔深度达到0.7倍模型高度即可达到破碎效果［6］.

尽管静态破碎技术十分适用于城区基坑挖掘，但对静态膨胀技术的裂纹可控工艺认识不足造成施工低效，故其市场价值认可度仍较低.一些学者试图改善其定向破裂能力来提高破裂效率.武尚俭等［7］研究了岩石类材料在5 种不同切口角下的裂纹扩展及其相互影响；宫志颖等［8］尝试应用切缝PVC 管对混凝土试块进行导向破裂，控制主裂纹方向；李敏等［9］采用导向钢管和内置钢片进行了裂纹导向试验；Luan 等［10］通过试块破裂试验观察了空孔在破裂过程中的导向作用；唐烈先等［11］通过导向模型试验，提出在膨胀孔中置入薄板控制混凝土静态破碎主裂纹方向的方法.目前破碎剂膨胀静力裂岩相关设计及施工方法仍沿用传统的钻爆法，采用圆形钻孔，这在一定程度上是裂岩低效的关键原因.相比钻爆法，静力破碎法只需软岩中形成裂隙间距适当的裂隙网络即可满足开挖需求.因此合理利用孔形参数，利用尖角应力集中效应将有限的膨胀能量集中在岩石薄弱处，是提升静力破碎技术定向能力和效率的关键.

本文研究了非圆异形钻孔在静力膨胀技术中的应用，设计并进行了物理实验，研究了该方法的基本规律.分析了定向裂缝的起裂、扩展过程和机理.在此基础上，利用颗粒流程序，进一步探讨单向致裂效果的最佳三角孔型.此外，探究了双孔联合作用的最佳间距以及岩石自身强度对压裂效果的影响.

1 室内试验

市场上常用的破碎剂是由碳酸钙和氧化钙组成的灰色粉状材料，与水发生化学反应后形成水化物.本次试验根据15 ℃的环境温度选用SCA-Ⅲ型静态破碎剂，水剂质量比为1∶3，充分搅拌后倒入直径为31 mm 的量筒中，温度变化和体积膨胀过程如图1所示.反应的初始温度为18.5 ℃，在前70 min温度缓慢升至29.3 ℃，由于量筒四周较为坚硬且上部存在大量空间，当反应进行至87 min 时，在105 ℃的高温下静态破碎剂迅速向四周膨胀并往上部溢出，最终体积膨胀大小约为初始值的3倍.

根据相关文献［12］，软岩试样的原材料选取水泥、细砂、中粗砂、石膏和水，通过配比试验确定其质量比为5∶18∶12∶5∶10，在室温条件下自然养护7 d，通过万能试验机进行单轴压缩试验获得其物理力学参数，如表1所示.

表1 试样物理力学参数Tab.1 Physical and mechanical parameters of the sgmple

根据相似原则选择尺寸为400 mm×400 mm× 200 mm 的长方体不锈钢模具，采取预留孔洞的方法制作单圆形孔的试样D和单三角形孔洞的试样A和试样B，采用同样的方法制作400 mm×500 mm×200 mm的试样C，如图2所示，四个灌装孔表面积相等，孔深均为150 mm，孔内体积均相等以确保获得的膨胀荷载总量是一致的.试样A 为边长40 mm 的正三角形钻孔，试样B 为顶角90°的等腰三角形钻孔，试样C为顶角120°的等腰三角形钻孔，试样D 为直径29.6 mm 的圆形钻孔，试样A、B、C 均沿横向、竖向及尖角平分线延长线方向等距布置3条应变监测线.

图2 试样及孔洞布置Fig.2 Samples and arrangements of holes

试验系统包括图像监测系统和静态应变测试分析系统两部分.将静态破碎剂与水按质量比3∶1 均匀搅拌3 min 后注满灌装孔.在3 条监测线上均等距布置3 组应变片，以0.5 Hz 的采样频率监测应变变化，同时用高分辨率数字影像定时记录试样表面宏观裂纹的发展.

2 试验结果分析

静态破碎剂（SCA）在钻孔中逐渐反应产生膨胀压力和释放热应力引起钻孔周围的径向压应力和拉应力增加.当产生的拉应力大于试样的抗拉强度时，试样开始出现裂纹，在细小裂缝的发展过程中，应力被释放并产生塑性变形，试样的抗内压能力被进一步削弱，进而形成损伤区，SCA 进一步膨胀，膨胀压力通过损伤区向外传播，损伤区的微裂纹不断扩展，从而使损伤区的范围逐渐扩大.

对于圆孔而言，理想情况下，孔壁周围因内压产生的拉压应力是均匀的［13］，膨胀压力不断增加后，由于试样的不均匀性，试样某些脆弱处优先产生裂纹，即出现优势破裂面，膨胀能量就会自动优先向优势破裂面处聚集，从而导致裂纹的发展.在本试验中，圆形孔洞试样D 在灌入破碎剂157 min 后出现两条对称的贯通裂缝，如图3 所示.当出现这两条裂缝后，膨胀能量优先聚集于此使得裂缝宽度不断发展，234 min 后达到最终破裂状态，裂缝最大宽度为15.84 mm，且无其他主裂纹产生.根据相关研究［14］，圆形钻孔的破裂模式主要有两种，一是出现2 条对称的贯通主裂缝，二是随机出现3 条贯通的主裂纹，进一步证明圆孔的随机寻优破裂机制.对于部分工程应用，这样的机制使得破碎效率降低，定向效果不理想.

图3 圆孔试样破碎过程Fig.3 Rupture process of the round hole sample

在正三角形钻孔破碎试验中，由于尖端处应力集中效应的存在，尖端处产生的径向拉压应力远大于其余光滑处，因此尖端的细小裂纹出现时间最早，在151 min 时有尖角端开始出现细小裂纹，如图4 所示.通常表面的裂缝总是急速出现，随着膨胀应力的释放，其他尖端表面也开始出现微裂纹，并沿着破裂面进一步扩展，最终正三角形钻孔试样A 的最大裂缝宽度为17.44 mm.

图4 三角孔试样破碎过程Fig.4 Rupture process of the triangular hole sample

由试样破碎结果可知，宏观裂纹的发展方向是有规律的，它们总是从尖角处产生并沿着角平分线延长线方向发展，在膨胀压力的不断释放下裂纹逐渐变宽，最终导致试样完全断裂.

对于三角孔而言，最小抵抗线距离W［15］并非等于尖角距自由面的最小距离，在试样A 中，控制三个尖角至边界的最小距离均为180 mm，裂纹1 先于裂纹2 和裂纹3 产生.裂纹2 和3 的发展历程几乎对称一致，而裂纹1 的最大宽度比它们高出52.3%，即裂纹1 得到了优先发展，这说明三角形钻孔中最小抵抗线距离为尖角角平分线延长线至自由面的距离.

这种沿角平分线定向破裂的规律适用于其他任意形状的异形钻孔，并且起裂时间随着尖角变小而缩短，顶角90°的等腰三角形孔洞试样B 起裂时间为147 min，顶角120°的等腰三角形孔洞试样C 起裂时间缩短为124 min，相比圆形孔洞试样的破碎效率，提升是可观的.

然而使用底角角度过小的三角形孔不仅会带来造孔方面的困难，也同样会影响定向破碎的效果.试样B 和试样C 保证了尖角的最小抵抗线距离相等，试样B 中90°尖角由于没有足够的膨胀能量驱动破裂面的产生，无裂纹产生，试样最终因45°尖角产生的对称裂缝贯通而断裂，这种双裂缝贯通的断裂模式在满足尖角最小抵抗线距离接近的前提下是稳定且可控的.而在试样C 的破碎过程中，初始裂纹并非出现在尖角而是在钻孔底部，这是因为尖角处产生的拉压应力急剧上升，在钻孔底部产生叠加效应，且此处最小抵抗线距离远小于尖角处，更有利于裂缝发展.非预计方向产生的裂纹对于膨胀能量具有消散作用，试样C最终的破碎效果劣于其余试样.

应变-时间曲线进一步揭示了三角形钻孔试 样在膨胀压力作用下的破碎规律.如图5 所示，在试样A 破碎过程中，前100 min 三条监测线的等距监测点及尖角处的应变都处于平稳状态，然后尖角处的应变εα4率先开始增长，第一条裂纹产生时达到403.8 με；145 min 后3 个监测点应变均开始增长，角平分线延长线处监测点应变εα3增长速率先低于横向εα1和竖向监测点εα2，这是由于此时破裂面还没有生成，膨胀能量的传递仍然具有随机性.起裂后膨胀能量的传递开始具有导向性，εα3增长速率发生跃进达到峰值时应变为285.5 με，而εα1和εα2依旧缓慢增长，峰值应变值为131.4 με和130.4 με.

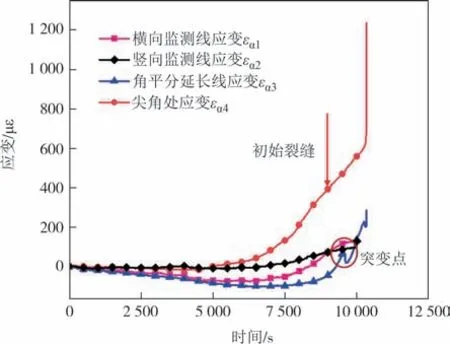
图5 试样A的应变-时间曲线Fig.5 Strain-time curve of sample A

综合试样A、B、C 的试验情况，可将三角孔洞静力膨胀破碎过程分为三个阶段：平稳发展阶段、快速增大阶段和衰弱阶段.如图6 所示，在平稳发展阶段，能量释放缓慢，各个方向的应变增长速率几乎没有差别.在快速增长阶段，一方面膨胀能量释放越发迅速，新的破裂面广泛形成且具备一定的方向性，因此角平分线处的应变迅速上升到最大值.相比圆形孔［16］，三角孔洞尖角方向的突变阶段更为迅速.在衰弱阶段，温度应力和拉压应力下降，断裂不断出现导致能量消散，应变快速下降.

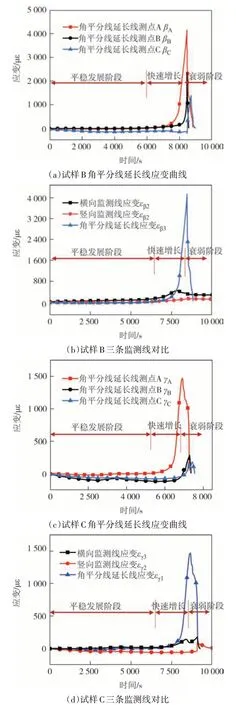
图6 试样B和C的应变-时间曲线Fig.6 Strain-time curve of sample B and sample

裂纹传播方向上的应变衰减剧烈，如图6（a）、（c）所示，试样B 的45°尖角平分线第二测点峰值应变衰减为尖角处的57.16%，第三测点峰值应变衰减为尖角处的33.41%.试样C的30°尖角平分线第二测点峰值应变衰减为尖角处的19.60%，第三测点峰值应变衰减为尖角处的12.46%.相较而言，尖角角度越小，尖角尖端处产生的峰值应变越大，试样在尖端处的破碎效果越好，应变能量衰减越迅速.

结合图7 及前述宏观裂纹观测结果，在一定范围内，小尖角造成的应力集中效应在缩短起裂时间上效果是显著的，并且产生了更大的峰值应变，使得整个破碎进程得到了一定加快.

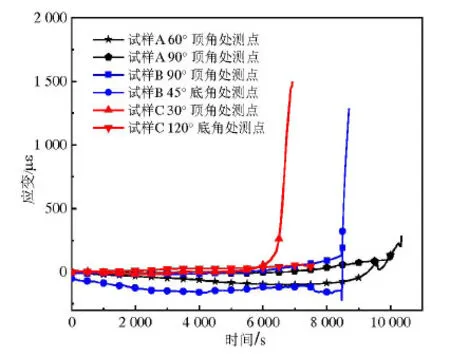
图7 三试样对比Fig.7 Comparison of three samples

三角形孔在膨胀压力作用下致裂岩石时，由于异形孔尖的应力集中效应，使得尖角处的破裂面最先形成，膨胀能量的释放寻得最优通道，在裂缝扩展过程中，总是倾向于沿着尖角角平分线延长线方向发展，因此不规则的尖角同时起到聚集和导向作用.这使得工程中可以寻得简单易造的钻孔如正三角形孔来代替传统圆孔应用于静力膨胀裂岩中，主导裂纹走向，提高裂岩效率.

3 颗粒流模拟

为了验证室内试验中异形孔裂纹发展的规律并进一步探究单向致裂最优尖角和双孔联合作用机理，采用颗粒流程序PFC2D进行数值模拟［17］.在数值模型中，以平行黏结模型模拟软岩(图8).平行黏结模型中的平行键可以在颗粒之间传递力和力矩.平行键可以设想为一组具有恒定法向和剪切刚度的弹性弹簧均匀分布在接触面上，并以接触点为中心.颗粒在接触处的相对运动产生法向应力和剪应力，如果超过相应的黏结强度，平行黏结就会断裂，黏结材料将连同其伴随的力、力矩和刚度从模型中删除.因此，平行黏结模型可以更准确直观地表现岩石的断裂过程，此外，通过对破裂过程中的微裂纹数量监测可以定量评价岩石破碎效果［18］.

图8 平行黏结模型原理Fig.8 Principle of parallel bonding model

试样组成为直径1.00～1.50 mm 高斯分布的颗粒，不断调整PFC2D程序中的微观参数，对照实验室单轴抗压强度的测试结果对模型微观参数进行了多次校准，最终标定结果如图9 所示，确定的具体微观参数如表2所示.

表2 PFC2D微观参数Tab.2 PFC2D Micro-mechanical parameters

图9 数值模型标定Fig.9 Calibration of numerical models

建立与室内试验同尺寸的单等腰直角三角钻孔数值模型，比较其破碎过程中裂纹发展的规律以验证模型的可行性，如图10 所示，数值模型裂纹发展的阶段及过程与室内试验的趋势吻合，最终破裂效果与室内试验一致.

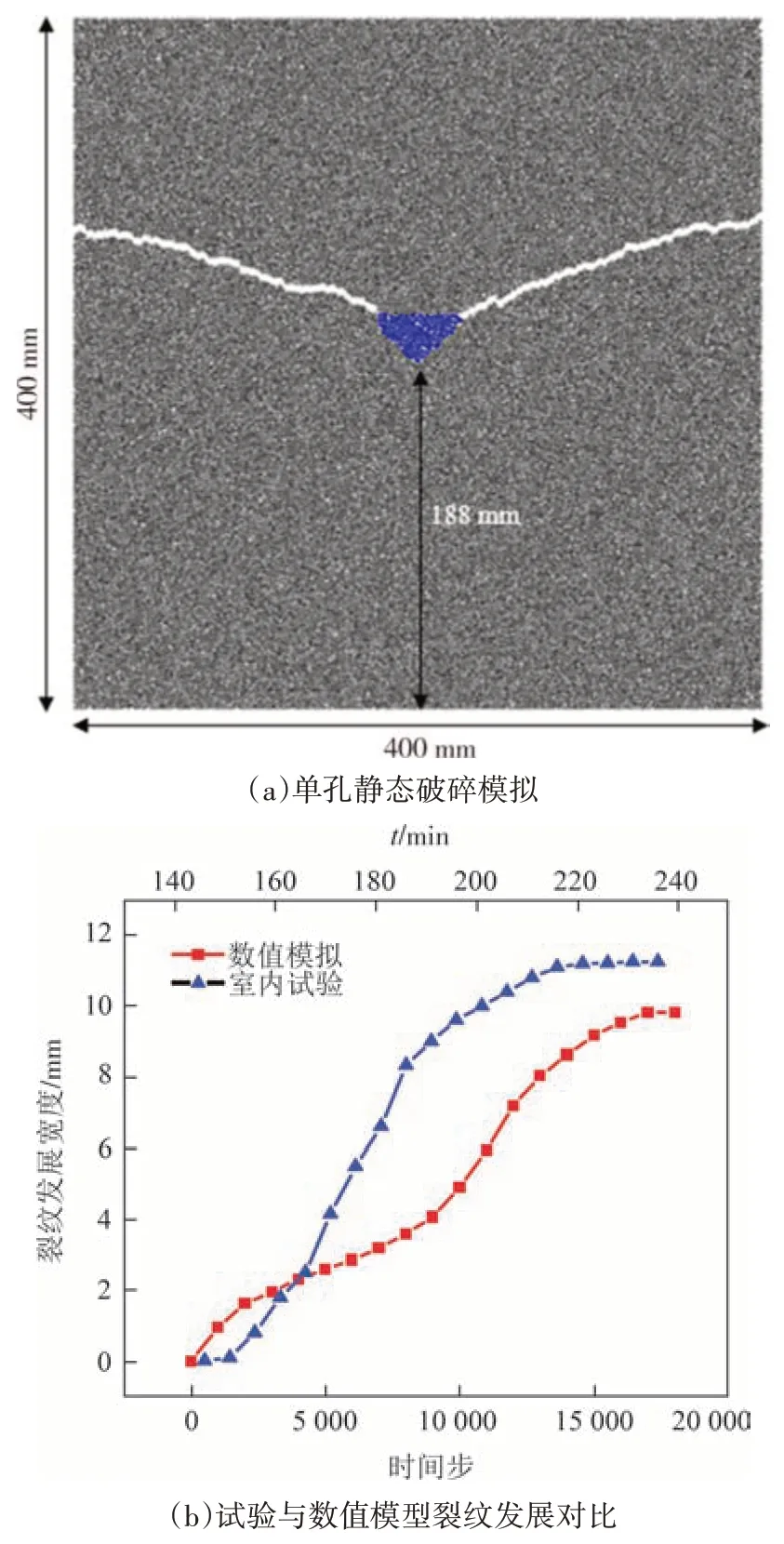
图10 数值模型裂纹扩展Fig.10 Crack propagation of numerical model

由于几何条件的限制，异形三角钻孔总存在小角度尖角及大角度尖角.运用数值模型对三角孔单向破裂最优尖角问题进行进一步探究，模型仍以等腰三角孔作为钻孔，改变其顶角的大小，并实时监测顶角处主裂纹的宽度，如图11 所示，20°顶角的等腰三角钻孔由于孔型修长，底边的微裂纹分散了一部分膨胀能量，不能稳定地形成顶角处主裂纹单向破裂的效果，因此其单向致裂能力逊色于30°顶角的等腰三角钻孔.

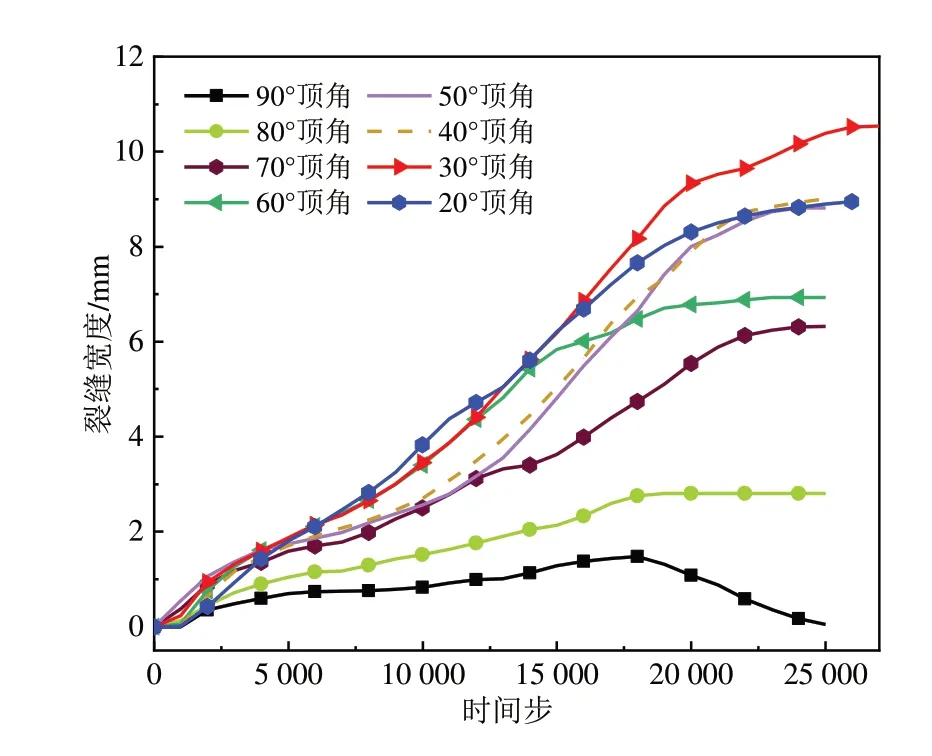
图11 不同顶角等腰三角孔的裂纹发展比较Fig.11 Comparison of crack development of isosceles triangular holes with different apex angles

在此基础上，对双孔联合作用的最佳间距展开研究，由于膨胀致裂是一个准静态过程，双三角孔的组合效应可以近似看作两个单孔在各自影响范围内的叠加.由之前的试验结果可知，尖角相对的双孔布置形式显然能够进一步强化裂纹的定向发展，但由于缺乏对单孔影响范围的认识，在数值模型中尝试不断改变双孔间距，来观察断裂效果的差异.模型选取尺寸为3 m×4.5 m，颗粒数为24 926 个，分别进行双正三角钻孔、单正三角钻孔和等面积等腰直角三角形钻孔的双孔膨胀破裂模拟.

在探究双孔间距影响的模拟中，一共完成了8组不同间距的试验，如图12所示，其中R为正三角孔边长大小.双孔洞破裂的宏观裂纹仍遵循单孔裂纹发展的规律，即起裂于尖角并沿角平分线延长线延伸，并在顶角连线范围内形成叠加效应.在两孔间距较小时，双孔间叠加的破裂影响范围较广，不仅在中间区域形成了更多的微裂纹，在左右边界也有微裂纹产生.当间距大于6R时，左右边界的微裂纹消失，说明此时双孔膨胀引起叠加应力场在左右边界处并没有达到胶结体的临界强度.而当间距达到8R时，上下边界也开始有微裂纹萌生.边界影响产生的微裂纹对尖角连线区域的破坏效果起削弱作用，因此当两孔间距7R时，双孔的叠加影响范围较为集中，裂隙在指定方向产生，即定向效果最佳.

图12 双正三角形孔微裂纹Fig.12 Double equilateral triangular hole microcracks

如图13 所示，微裂纹的数量随着间距的增大呈先增后减的趋势.边长40 mm 的双正三角孔在膨胀荷载的作用下破坏选定尺寸的试样时，尖角间距为3R时，产生的微裂纹数量最多，即破碎效果最佳.同理，在正三角和等腰直角三角形孔洞联合作用下，孔间距为6R时破碎效果最佳.

在控制双孔间距为7R的前提下，进一步探究岩石抗压强度对双三角孔致裂效果的影响［19］，如图14所示，选取单轴抗压强度为1～30 MPa 的模拟岩石，分别进行双正三角钻孔的膨胀破碎，对最终数据点进行拟合，结果显示破碎效果和岩石强度呈乘幂关系，方差为0.99.进一步表明，对于强度较低的软岩，异形孔膨胀裂岩是相对有效的开挖手段.

图14 岩石强度对破碎效果的影响Fig.14 Influence of rock strength on crushing effect

4 结论

本文利用异形孔独特的力学特性，通过室内模型试验，重点研究了三角孔在膨胀荷载作用下定向致裂岩石的规律，在此基础上利用颗粒流软件进一步分析双孔间距及岩石强度对破碎效果的影响，并得出以下结论：

1）在膨胀压力作用下，异形孔试样的起裂和破碎时间均短于圆形孔，并且其裂纹的发展是可控的，总是沿着尖角的角平分线延长线方向进行.

2）利用顶角大小不同的等腰三角孔可以实现裂纹单向或双向发展.根据应变的变化，可将试验分为三个阶段：平稳发展阶段、突变增长阶段以及衰弱阶段.

3）双孔联合作用下，破碎效果随着间距的增长先增强后减弱，双正三角形孔洞间距为7 倍边长时定向致裂的能力最强.岩石强度和最终破裂效果呈乘幂关系.