基于遗传算法的家庭活动-出行决策研究
何保红 ,段玉琳,郭 淼
(1.昆明理工大学 交通工程学院,云南 昆明 650500;2.北京工业大学 城市交通学院,北京 100124)
0 引 言
随着交通设施建设趋于饱和,城市交通规划开始由“设施规划”向“政策设计”转型[1]。通过调控出行者出行决策过程,促使城市宏观交通总量、出行结构和时空分布趋于合理,正成为交通领域重要的政策调节手段[2]。个体作为家庭网络中的一员,在行为决策时既不能脱离客观物质环境,也不能脱离与家庭成员交互的微观社会情境[3]。传统以个体为单元的行为研究,往往忽视了家庭微观社会情境中存在家庭成员之间互动会对个体行为产生影响这一事实,导致难以准确客观分析城市交通需求变化和预见交通政策实施效果。
近年来,国内外交通学者开始关注家庭成员交互与个体活动-出行决策间的关系。C.HO等[4]针对家庭交互行为中较为显著的联合出行,采用嵌套Logit模型探究了家庭联合出行与个体出行方式选择间的关系,发现联合出行受家庭资源、活动类型等要素影响;Y.O.SUSILO等[5]通过建立家庭时间分配模型,发现活动-出行时间在家庭成员间存在交互,且这种时间分配不仅是个人决定的结果,也是家庭内部成员之间互动的结果;J.X.FENG等[6]通过构建有序Probit模型分析发现,与老年人同住的家庭成员用于工作和休闲活动的时间普遍较长,家庭中有老年人存在会在一定程度上影响个体活动-出行行为。
蒋晨等[7]通过多元受限因变量模型,探究家庭活动参与和性别差异之间的关系,发现家庭中女性出行行为不仅受自身活动安排影响,还与其配偶的出行行为有关;何保红等[8]通过构建结构方程模型,探究老年人对家庭成员日常活动-出行行为的影响,发现随着老年人对家庭贡献度增加,其他成员在家务活动上的分配时间减少,自由活动时间增加;A.ERMAGUN等[9]、W.ADAM等[10]关注到家庭中儿童的特殊性,利用出行链刻画其行为特征,探讨了家庭成员受到的时空制约与接送儿童之间的关联性,发现家庭接送儿童行为不仅取决于儿童自身能力,还取决于家长工作地时空制约。上述研究虽然认识到家庭成员间的互动会对个体活动-出行决策产生影响,但关注的焦点大多落在外部因素对决策层级的影响,缺乏对家庭成员间的内部交互进行深入剖析。
鉴于此,笔者在时间地理学的基础上结合最优化理论,将家庭联合活动视为在特定时空制约下,成员间通过相互协作做出效用最大化的活动安排和出行选择结果。通过构建家庭活动-出行决策模型,以期最大限度还原个体活动-出行选择行为,并以此为新时期“以人为本”的交通规划和交通需求预测提供科学参考。
1 家庭活动-出行特征描述
家庭作为个体日常活动-出行决策的基本单元,其外部环境及内部属性的变化会改变个体的日常活动-出行行为。在这一过程中,家庭成员会通过利他主义在一定程度上平衡自身或他人所受到的制约,以陪伴、互助和替代等形式帮助个体更好完成活动-出行计划[11]。这种联合特性在个人层面是隐藏的,难以通过个体行为,透视家庭活动-出行行为背后复杂的决策过程。为深入剖析个体活动-出行背后决策过程,将个体活动-出行行为置于家庭中观察,家庭活动-出行决策过程及联合活动解构如图1。在时空制约和活动需求作用下,个体视角下活动-出行决策维度较为单一,家庭成员出行链之间彼此相互独立,不存在交织与嵌套现象,难以体现活动的联合特性,也就无法从中透视家庭联合活动-出行背后决策过程。相较于个体视角,家庭视角下的活动-出行决策主体和行为模式更为丰富,家庭成员出行链之间不仅存在交织与嵌套现象,而且更能体现活动联合特性。

图1 家庭活动-出行决策机制及联合活动解构Fig.1 Family activity-travel decision-making mechanism and joint activity deconstruction
从上述分析中可以看出,家庭具有一定自我调节功能,即在外在环境制约下,家庭会通过成员间互助协作以平衡外在制约。若仅从个体视角,则难以透视这种交互关系,而将活动-出行置于家庭中观察时,家庭成员在活动-出行决策上存在着交互关系,在这种关系作用下将会产生家庭视角特有的联合活动模式,主要包括陪伴活动、接送活动和替代活动,具体特征分析如表1。
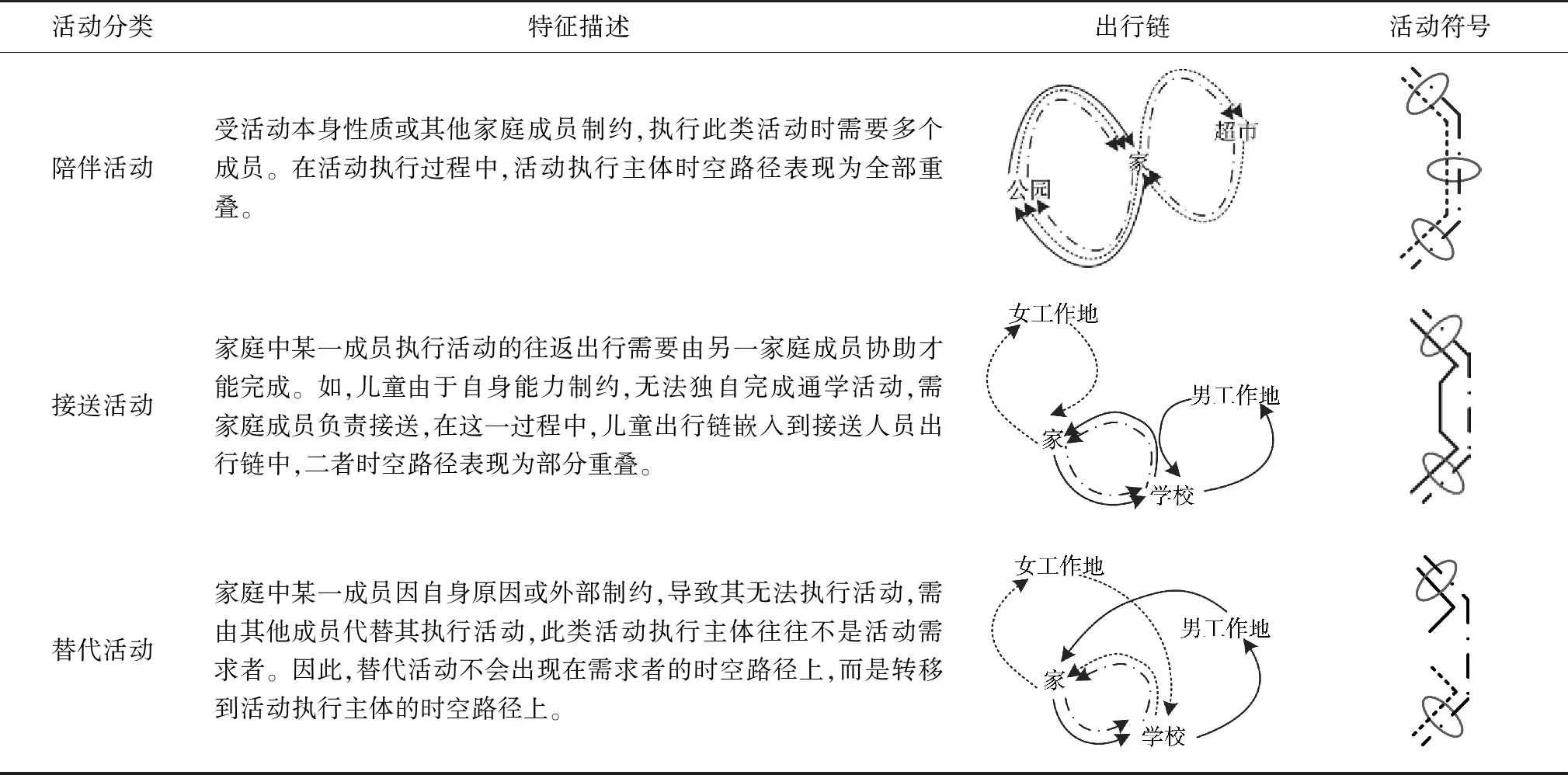
表1 家庭联合活动特征描述
2 家庭活动-出行决策模型
2.1 问题描述
CHAPIN认为个体活动-出行决策是在一个时空连续体内发生的一系列有序的活动,涉及活动-出行的要素决策包括:活动类型、活动位置、活动顺序以及出行距离等[11]。事实上,活动-出行决策过程才是导致决策行为结果的源头与核心,家庭交互决策行为本质上是特定时空制约下,以交互关系为介质,以均衡成员间制约为目标的家庭内部自组织现象。
2. 活动符号来自于文献[12],表示成员间活动-出行时空过程的联合性。
家庭活动-出行决策问题可以描述为多个成员在有限的家庭资源下,通过彼此间互助协作完成家庭活动的过程。由于决策个体增加,在家庭成员彼此间交互作用下,个体活动-出行时空路径扩展为与他人时空路径的重合来表征其联合特征。
通过扩展决策变量以表达不同家庭成员的出行链,从出行上体现家庭成员间的关联性;引入相容参数以实现家庭成员和活动类型的匹配,从活动上体现家庭成员间的关联性;出行时间、活动开始和结束时刻是家庭成员进行活动-出行决策时的重点考虑因素,应将其纳入目标函数中;由于外部环境主要是从时间和空间的角度对成员的活动-出行决策施加制约,将具有代表性的活动时间窗、活动空间位置等转化为模型的主要约束条件,系统建立家庭联合活动-出行决策效用模型。
2.2 参数图示
基于家庭的活动-出行决策是家庭成员在外部环境制约与内部成员交互作用下,共同做出的活动安排和出行选择(图2),家庭活动-出行决策过程主要涉及决策变量、决策环境与相容参数。

图2 家庭活动-出行决策过程中涉及参数Fig.2 Diagram of parameters involved in household activity-travel decision-making process
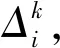
2.3 模型建立
在时间地理学时空制约思想和最优化理论基础上,兼顾家庭活动-出行决策过程中出行效用与活动效用,以实现家庭效用最大化为目标,建立家庭活动-出行决策模型,模型中涉及参数如表2。
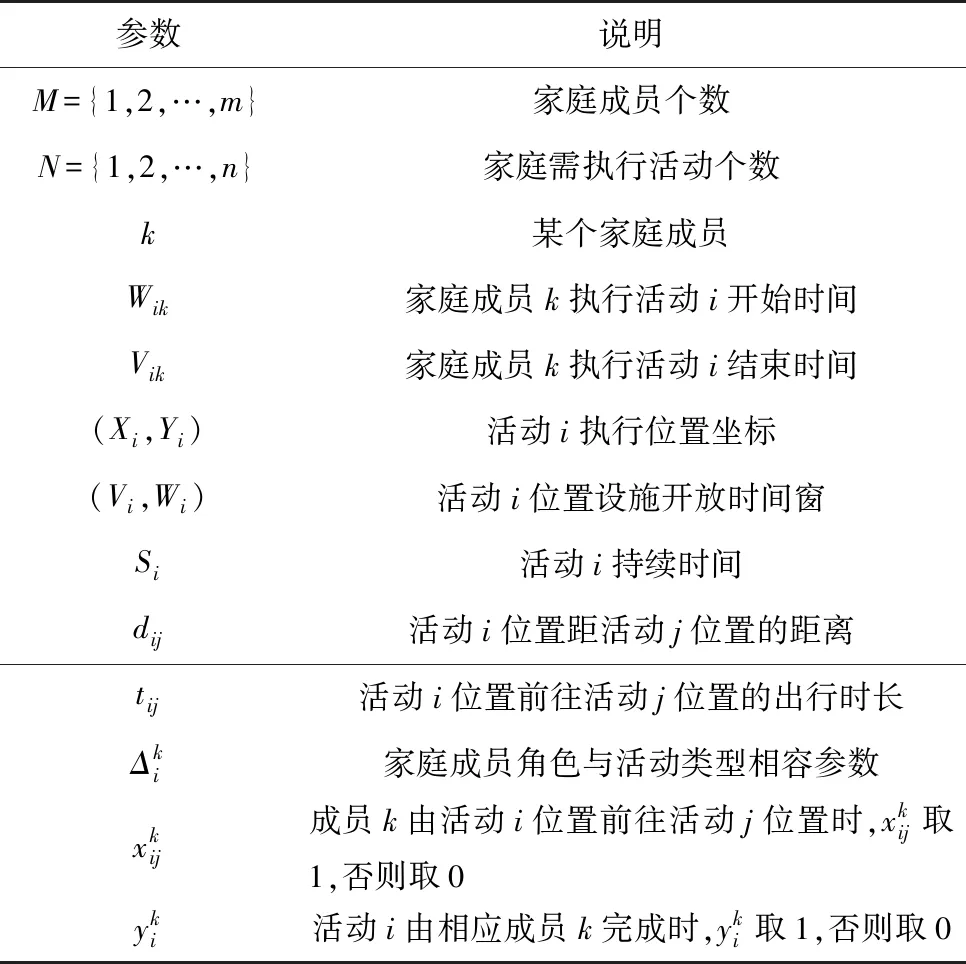
表2 模型参数说明
模型具体形式如下:
U=max(U1+U2)
(1)
式中:
(2)
(3)
式(1)~式(3)为目标函数,式(1)表示家庭成员在出行过程中执行活动的效用最大;式(2)表示家庭成员在相邻两个活动位置之间的移动时间最短;式(3)表示家庭成员执行活动的持续时长。
约束条件:
(4)
(5)
(6)
(7)
(8)
(9)
(10)
Vi≤Wik,Vik≤Wi
(11)
(12)
Vik-Wik=Si, ∀i∈N, ∀k∈M
(13)
(14)
(15)

2.4 模型求解
遗传算法是一种较为完善的启发式算法,受自然界进化论启发,该算法将种群中所有个体作为对象,对所有个体的染色体进行编码后实施选择、交叉、变异操作以生成下一代,持续重复此过程,直至满足预先设定的收敛标准,即得到问题的解[13]。与此同时,遗传算法可以针对实际情况对参数进行调整[14],使得其有较高的使用灵活性与应用广泛性。
大量实践表明,遗传算法在求解多目标优化问题方面有显著成效。考虑笔者所建模型为寻找使家庭活动-出行效用最大化的家庭成员活动-出行安排,属于组合优化问题,因此,使用遗传算法为每个家庭成员安排最优活动-出行方案分配,以实现整个家庭活动-出行效用最大化。
模型进行求解思路为:假设家庭中所有活动都需要完成,工作活动应由相对应人员完成,活动执行必须要满足前一个活动最早结束时间及中途移动时间要早于后一个活动最晚开始时间。求解步骤如下:
步骤 1参数初始化。结合模型特征,经过多次试验最终确定求解相关参数如下:种群初始化数量为40,最大迭代次数为30,交叉概率为0.9,变异概率为0.000 1。考虑到实际出行方式的多样性,结合模型验证数据特征,参考昆明市城市道路交通工具运行速度特征将不同交通方式的出行速度值设置为:小汽车35 km/h,电动助力车25 km/h,自行车10 km/h,公交车20 km/h,步行4 km/h。
步骤 2染色体编码及初始化。借助MATLAB编程,采用整数编码方式,对需要执行的活动和家庭成员进行编号。0表示家,1、2分别表示男、女家长工作,3、4分别表示接、送儿童,5、6、7分别表示家庭中3个成员,5为男家长,6为女家长,7为儿童。假设所有成员均从家出发并最后回到家,故在编码中进行简化将0去除。此外,接送儿童作为家庭中典型的联合活动,需要家长和儿童共同参与完成,因此在编码中分别设置两个3和4分布于染色体中,表示家长和儿童联合参与,如图3。
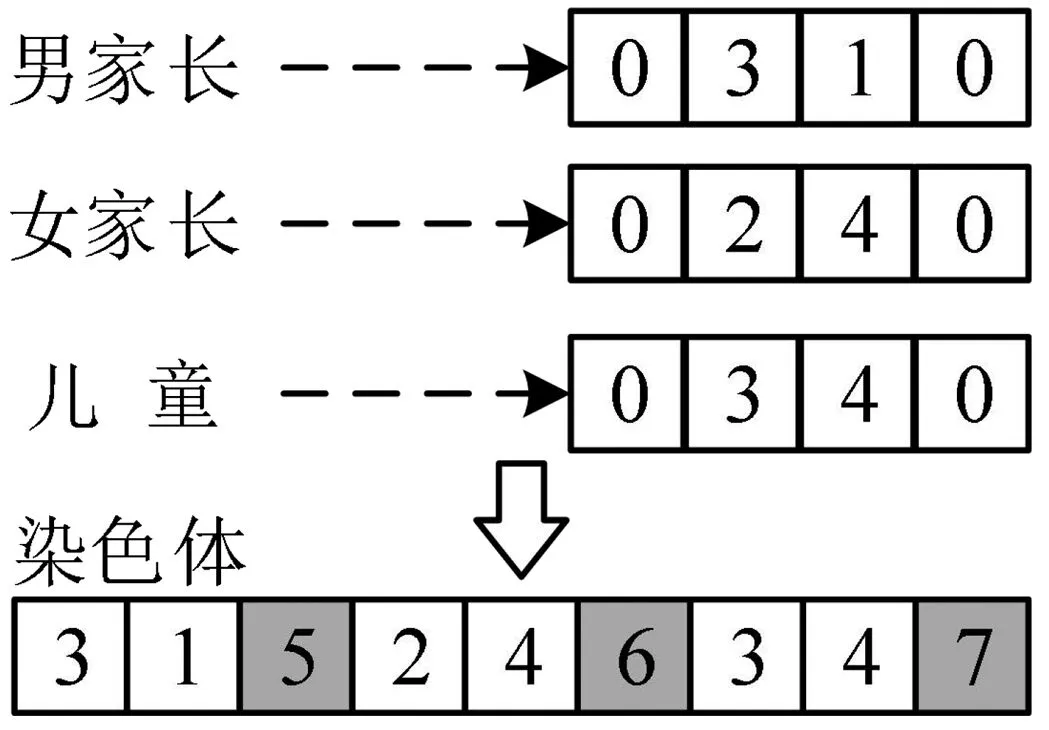
图3 染色体编码方案Fig.3 Chromosome coding scheme
步骤 3染色体排序。将家庭中所有成员的活动位置空间坐标、活动时间窗及出行方式作为输入集,根据约束条件进行遗传操作,输出排列好的编号即为出行链,详细步骤如下:
1)选择算子,采用轮盘赌选择,根据个体适应度值大小决定其在下一代中的存活概率;
2)交叉算子,结合笔者采用的编码方式,为避免染色体在任意位置进行交叉,导致新个体中存在基因缺失和重叠产生无效解,采用单亲交叉算子(图4),使交叉操作在一个个体上完成,以保证子代个体基因的有效性和完整性。对于不合法的编码则重新进行交叉操作,直到产生符合条件的染色体序列;
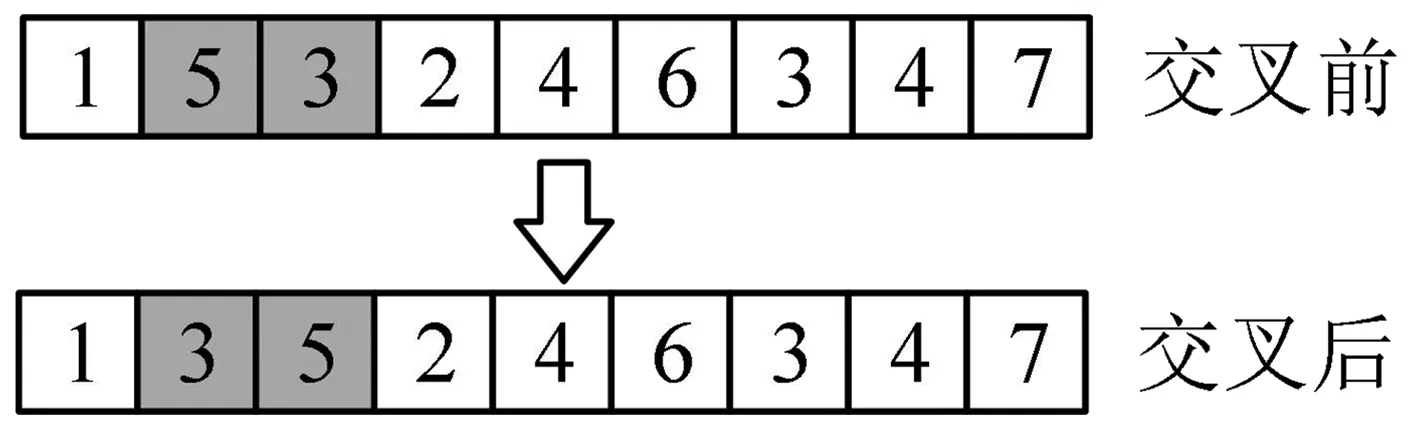
图4 交叉示意Fig.4 Schematic diagram of crossing
3)变异算子,通过随机对染色体进行交换或插入产生新的个体,完成变异操作。
步骤 4计算适应度。将式(2)、式(3)计算之和作为适应度值,选取适应度值最大时输出的出行链作为模型求解结果。
3 实证结果分析
3.1 数据来源
实证数据来源于2016年昆明城市居民出行调查,调查包括个人信息、家庭信息,以及居民整日活动-出行数据。依据笔者研究目标,考虑到所建立决策模型需要体现家庭联合决策特点,而城市儿童接送行为则较能体现家庭成员联合决策特点,故从中选取500个存在儿童通学出行需求的核心家庭所有成员整日活动-出行数据作为模型验证样本。需要说明的是,500个样本家庭当日均有联合活动,其中,445个家庭存在接送活动,剔除完成接送活动后及时返回家且不从事通勤活动的样本家庭,将余下327个家庭作为验证样本。除去存在接送活动445个家庭,余下55个家庭存在替代活动,替代活动的判别是依据接送儿童活动分别嵌套在男女家长的出行链中。利用存在接送活动的327个家庭验证模型在基础场景中的正确性;为进一步验证模型的有效性,用存在替代活动的55个家庭验证模型在扩展场景中的适用性。
3.2 场景描述
3.2.1 基础场景
家庭中共有3名成员,分别是男家长、女家长和儿童,共有4项活动需要执行,分别是男、女家长的工作活动、送儿童上学、接儿童放学,接送儿童活动均由同一个家长完成。
3.2.2 扩展场景
家庭成员组成及需执行活动与基础场景相同。不同的是,扩展场景中男女家长一方执行了送儿童上学活动,但由于其下班时间与学校放学时间相隔较大,不能在规定时间内到达学校接儿童放学,导致需要由另一位家长替代完成接儿童放学活动。
3.3 结果描述
采用遗传算法求解模型,若求解输出结果与实际出行链一致,则模型验证成功,并对两种场景下家庭活动-出行行为进行解构分析。
选取基础场景中一个验证成功的家庭进行时空路径分析(图5)。女家长07:30顺路送儿童去距家2.8 km的学校上学,之后行驶2.7 km到达工作地,16:00离开工作地前往学校接儿童,16:30从学校回家;男家长07:30独自前往距家6.7 km的工作地,16:07离开工作地返回家。就活动时空临近性而言,儿童学校不仅与女家长工作地在空间上较为临近,且上下学时间也与女家长上下班时间较为接近。可见在家庭活动-出行决策过程中,在时间允许的情况下,为使家庭活动得以完成,通常将接送儿童活动分配给空间位置距离学校最近的家庭成员,最终以顺路接送模式完成该类活动,以减少对其他成员出行的制约。依次对类似的327个家庭进行出行链求解,发现有248个家庭符合,符合率为75.84%,即模型设定目标函数符合大多数家庭活动-出行情况。
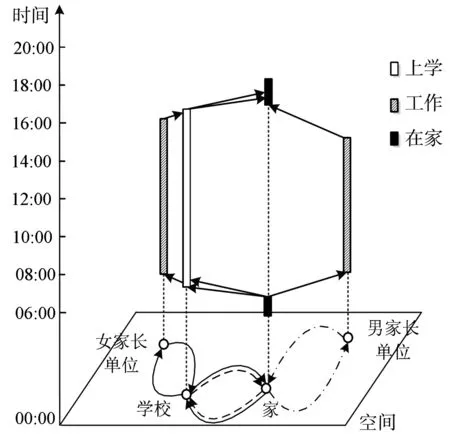
图5 基础场景中成员活动-出行时空路径Fig.5 Spatio-temporal path of member's activity-travel in normal scene
选取扩展场景中一个验证成功的家庭进行时空路径分析(图6)。女家长07:20顺路送儿童去距家2.8 km的学校,之后再行驶0.8 km到达工作地,18:00离开工作地返回家;男家长07:30从家出发前往距家1.6 km的工作地上班,16:30从工作地前往距工作地2.5 km的学校接儿童。就活动的空间邻近性而言,女家长工作地较男家长工作地离学校更近,但女家长下班时间晚于儿童放学时间,导致其不能在儿童放学前到达学校接儿童。考虑到儿童上下学安全性,避免儿童放学后长时间滞留学校,家庭中符合接儿童放学条件的男家长替代女家长接儿童放学。从个体视角看,男家长为完成接儿童放学活动,额外增加出行距离并导致出行时间增加,不符合个人活动-出行效用最大化原则的,但从家庭视角看,是因为女家长不具备完成接儿童放学活动,将活动转移至男家长出行链中,使家庭活动得以完成。由此可见,在家庭中会存在一定的利他主义,即为协助某一成员完成活动,通常会迫使其他家庭成员付出较高的时空成本。依次对存在替代活动的55个家庭进行出行链求解,发现有46个家庭符合,符合率为83.64%。即模型设定目标函数符合大多数家庭活动-出行情况,也说明模型具有一定动态性,能及时响应输入条件变化并做出调整。
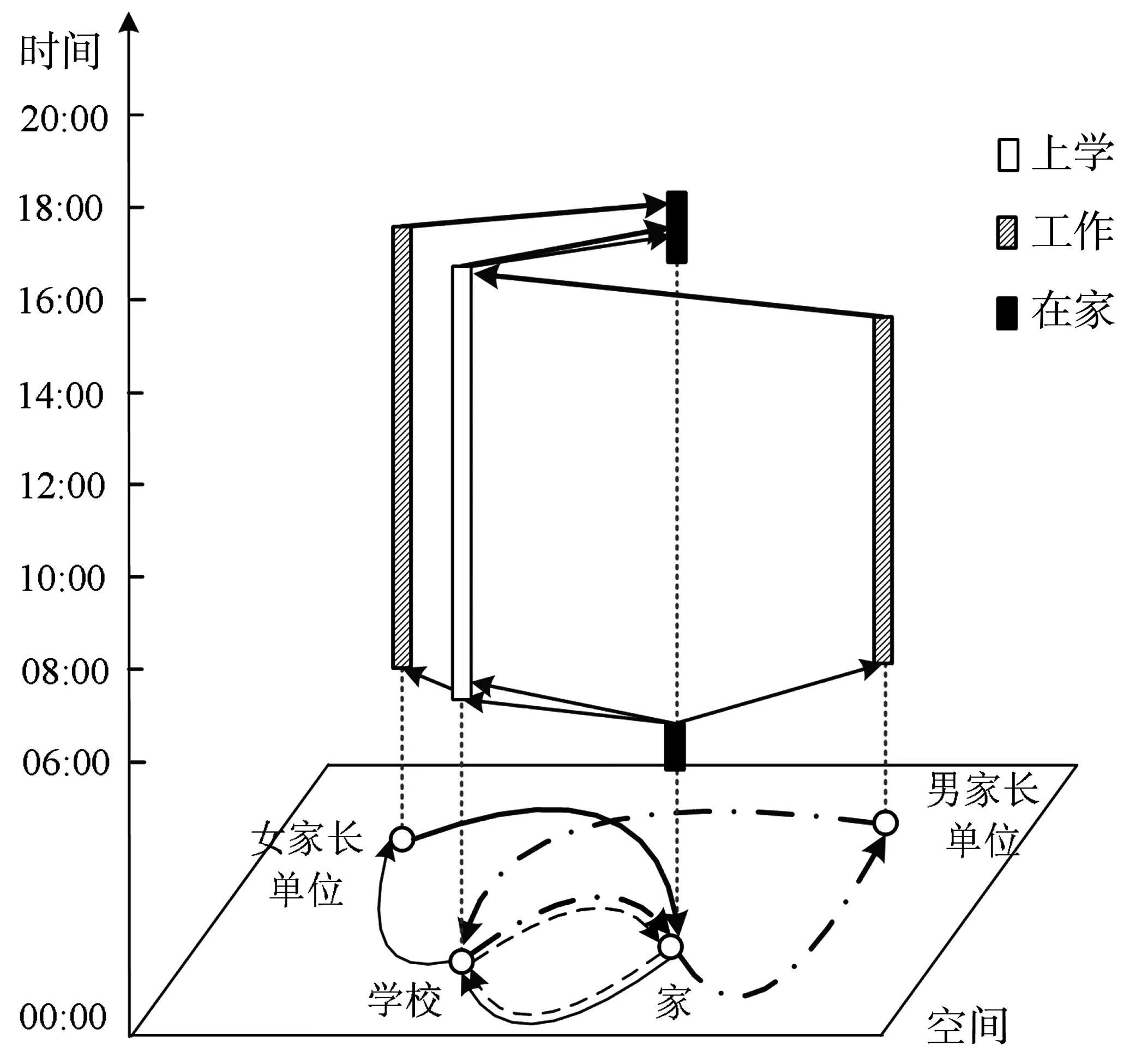
图6 扩展场景中家庭活动-出行时空路径Fig.6 Spatio-temporal path of member's activity-travel in extended scene
此外,笔者对验证不符的家庭进行剖析,发现这些家庭主要存在以下2类特征:
1) 家庭在指定儿童接送人员时可能考虑了时空邻近性,但出于对儿童安全性的考虑,小汽车使用者更可能会通过付出较高的时空成本而成为接送活动的执行者,这与王侠等[15]对通学出行研究结论基本吻合,也从侧面证实了小汽车在可达性和安全性方面比其他交通工具更具优势,这类家庭占比高达50.34%;
2) 受传统“男主外,女主内”家庭责任分工影响,女性比男性更有可能会承担接送儿童任务,女性因其自身特点而在家庭交互关系中呈现独特性,照顾儿童、接送儿童的可能性更大。在不具备时空邻近性条件下,可能会通过将出发时间提前或借助机动化方式等完成接送活动,这与塔娜等人[16]对城市女性日常出行行为研究的结论基本吻合,这类家庭占比为32.76%。
4 结 论
以时间地理学方法和最优化理论为基础,构建了家庭活动-出行行为决策模型,通过对不同时间情境的实证分析得出结论如下:
1)基础场景中有75.84%的家庭模型输出结果与实际出行链相符,而扩展场景符合率为83.64%,表明了所建模型的合理性和适用性。
2)家庭成员交互对于出行者的活动-出行决策以及执行具有重要影响,将通过家庭关系使不同成员的活动-出行过程在时间或者空间上发生部分或全部重叠。当某一家庭成员无法完成该活动时,家庭会通过成员之间的依赖性进行传递,由其他成员以替代活动的形式进行协助,以实现家庭成员时空制约的平衡。

