基于Shapley值分配原则的铁路应急资源调度研究

汤兆平,邹 扬,刘钰玲,孙剑萍

(1. 华东交通大学 交通运输工程学院,江西 南昌 330013;2. 宁波市轨道交通集团有限公司,浙江 宁波 315101)

0 引 言

随着我国铁路路网密度的持续增大,列车运行时速不断提高,行车组织愈加复杂,路网之中出现多个地点同时发生事故的可能性也逐渐增大,如遇到特殊地形地质或自然灾害时,更容易引发大规模的铁路突发事故。由于事故发生存在不确定性,以及铁路应急资源的储备成本高等特点,各救援点的应急资源不可能无限制配备[1]。因此,针对救援初期资源不足的情况,对多事故点多救援点的资源公平调配问题的研究显得尤为重要。

在多事故点-多资源-多救援点的应急资源分配调度方面,相关学者已进行了一定的研究。如王东海等[2]通过TOPSIS模型来评估事故点的救援优先权,模型中以成本系数和时间系数的形式表示事故点的优先权,使救援优先权较高的事故点优先获得其所需的资源。范雪琳[3]以应急控制程度最大化和线路停运损失最小化为目标,研究了铁路接触网多故障的资源调度问题;王旭坪等[4]以效用满意度和需求满意度为目标来描述并求解救援初期的应急物资分配问题;CHAI Gan等[5]提出了一种以救援路线行程时间估计为依据的应急救援资源调度方法,根据应急救援路径的总长度与救援车辆排队在时间上的延误的对应关系,计算出救援路径行程的大致时间,并以此为据建立改进的资源调度模型;汤兆平等[6]考虑事故点的需求为模糊需求,运用塔木德公平分配理论对大规模铁路突发事件下多事故点-多救援点-多种资源的资源分配问题,基于此分配原则进行资源调度,可以较好地保持博弈规则的公正性;陈治亚等[7]通过AHP模糊综合评价法对铁路多事故点的受灾程度进行评分,并以运输成本和惩罚成本最小化为目标建立资源调度优化模型。Shapley值分配原则能够兼顾公平与效益,已有学者对其在收益分配机制方面进行了研究。张宇翔等[8]通过考虑项目内部成员的产权比例、风险承担和工作贡献,构建了国际高铁项目收益分配概念模型,并采用合作博弈理论和Shapley值法对收益分配方案进行了修正;WANG Yuanhua等[9]研究了在n人合作对策下的对称和加权Shapley值,利用博弈者定义的非对称权重设计加权Shapley值的收益函数,从而保证最优分配是纯Nash均衡;赵璇[10]针对产学研联盟收益分配中存在收益值的不确定性以及联盟的不稳定性2个问题,使用估计值来衡量联盟的收益,建立了基于H-Shapley值法的产学研联盟收益分配模型,得出的H-Shapley分配解能够使产学研联盟合作保持长久稳定;杨靛青等[11]利用Choquet积分定义模糊合作对策中局中人可能形成的多层级联盟结构,在此基础上提出Shapley值解概念及其解法,通过算例分析合作对策Shapley值和Banzhaf值的异同特性,结果表明Shapley值的联盟结构相对固定;武士超等[12]通过熵值法和Shapley值法对快递行业组建末端配送联盟利益进行分配,最后对影响因素权重进行修正,得到最终分配结果,结果符合个体理性和集体理性;K.M.CUBUKCU[13]证明了在合作博弈框架下发展起来的Shapley值公平分割方案,可以实现土地所有者之间剩余开发权的公平分割。

笔者将Shapley值分配原则引入铁路应急资源的分配中,通过计算出各事故点对不同资源的Shapley值以确定分配比例和分配量,再综合考虑调度时间和调度成本等因素建立优化模型,最后进行模型求解。使调度方案实现公平与效益的统一,在减小系统综合损失的同时,该种分配方案也更易被多方接受。

1 Shapley值分配理论

假设合作博弈系统内有n个成员,由N={1,2,…,n}表示,不同成员之间互相排列组合成不同的联盟S(S⊆N),特征函数w(S)为联盟S的收益,w(S)具有超可加性,其性质表示为:若联盟S1和S2之间没有交集,则S1和S2合并形成新联盟的收益应该不小于联盟S1与S2的收益之和[14]。即:

(1)

联盟内成员i的收益为该成员i在所有联盟的参与中创造的边际贡献均值,表示为φi(w):

(2)

式中:S为包含成员i的所有子联盟;|S|为子联盟S中成员的个数;w(S{i})为子联盟S除去成员i后的收益;w(S)-w(S{i})为成员i对子联盟S的边际贡献;θ(|S|)为联盟S出现的概率,其计算公式为:

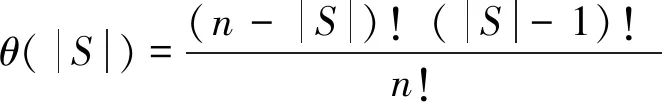
(3)

2 问题描述

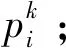
3 多目标优化模型建立

为了方便计算,笔者只考虑由于事故造成的直接损失。由于铁路应急救援具有紧迫性,因此优化模型目标函数的主要考虑因素是资源调度的时间最短,其次还应该尽可能使资源的调配成本最小。

根据上述分析,建立多目标优化模型如下:

(4)

(5)

(6)

(7)

(8)

(9)

(10)

模型中:式(4)为救援时间最短的目标函数;式(5)为总调度成本最小的目标函数;式(6)为事故点i和救援点j之间构成事故点-救援点对;式(7)为事故点i和救援点j之间不构成事故点-救援点对;式(8)为应急救援点向事故点实际运送应急资源的量等于救援点对该事故点应急资源的调运量总和;式(9)为应急救援点向事故点实际运送应急资源的量应该小于或等于救援点j的资源储备量;式(10)为救援点向事故点的实际运送量应该不小于0。

4 基于Shapley值分配原则的需求点资源分配数量的确定

将事故点的应急救援工作类比于合作博弈问题,其中的事故点可看作博弈问题中的参与方,应急资源的分配可看作参与项目的过程,各事故点由于应急资源得到满足所减少的损失可类比于参与到项目中获得的收益。

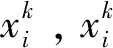
1)列举出所有包含事故点i的救援方案S,分别计算各个救援方案S下所减少的损失为:

(11)

2)计算在救援方案S中除去事故点i后所减少的损失为:

(12)

3)计算得到事故点i在救援方案S下的边际收益为:

(13)

4)根据式(2)得出事故点i对资源k的Shapley值为:

(14)

5)重复上述步骤,分别计算得出各个事故点i(i=1,2,…,n)的Shapley值,从而得到在现有的资源k总储备量条件下各个事故点的资源分配比例为:

(15)

6)设y为规模比例系数,各个事故点对k资源需求量、分配比例与规模比例系数乘积之和应该与k资源的总储备量相等,即:

(16)

7)根据式(16),可以得到y的具体数值,进而可以确定各个事故点i对k资源的具体分配数量为:

(17)

5 实例分析

5.1 实例概况

以中国铁路某局集团公司为例,其局内设共有14个应急救援基地(A1,A2,…,A14),为了便于计算,假设在某局的部分区域内突发铁路大规模事故,涉及的事故点有3处,分别用N1,N2,N3表示,参与救援的救援基地有5处,分别用M1,M2,…,M5表示。假设该事故中事故点需要的应急资源有医疗救援设备k1和铁路抢修设备k2两种。考虑到铁路货运单位千米运费以及救援时间成本,将单位救援物资和单位千米的运费设为c=7元,通过参考相关实例并根据决策者的偏好合理假设,将调运时间、调运成本的权重分别确定为ξ1=0.3,ξ2=0.7。各个救援点与事故点之间的信息如表1。

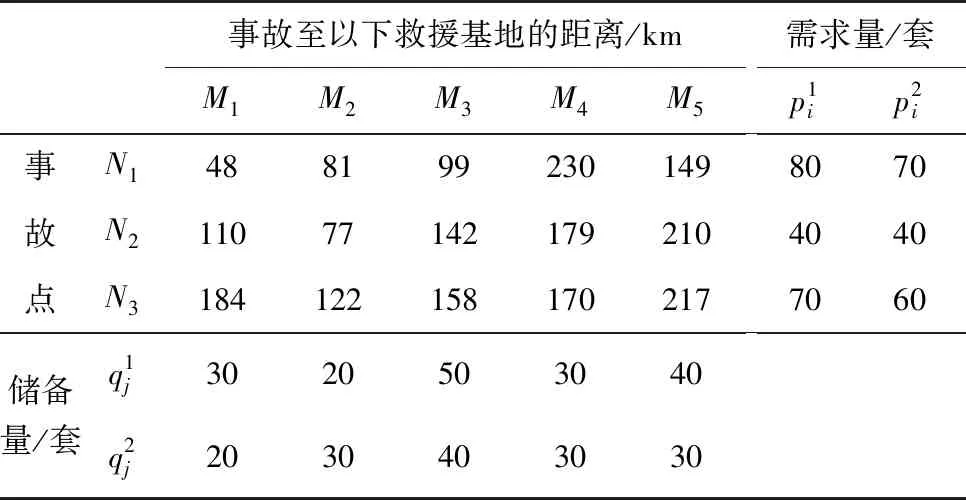
表1 各救援点和事故点信息

5.2 确定各需求点的实际分配数量

5.2.1 资源k1

表2 各事故点由于资源k1未能得到满足引起的损失

计算各个事故点对资源k1的Shapley值。

设y1为资源 的规模比例系数,已知资源k1的总储备量为170,根据公式(16),有:(80×37%+40×24%+70×39%)×y1=170,从而得到y1=2.56。

最后根据式(17)计算得到资源k1的实际分配情况如表3。

5.2.2 资源k2

表4 各事故点由于资源k2未能得到满足引起的损失

计算各个事故点对资源k2的Shapley值。

设y2为资源k2的规模比例系数,已知资源k2的总储备量为150,根据公式(16),有:(70×39%+40×26%+60×35%)×y2=150,从而得到y2=2.55。

最后根据式(17)计算得到资源k2的分配情况如表5。

表5 资源k2分配情况

5.3 调度方案的最优解

表6 最优调度方案

将优化后的结果代入式(4)和式(5),并根据调运时间以及调运成本的权重ξ1=0.3,ξ2=0.7,计算得到本次救援的最小综合成本为194 221.3元。

6 多种分配方法下的比较分析

在资源公平分配方面,主要有约翰·罗尔斯的公平分配理论、亚里士多德的分配正义理论、Shapley值分配理论以及塔木德公平分配理论。

为了体现Shapley值分配原则在铁路应急资源调度方面的良好适用性,下面以资源k1为例,对比分析比例分配理论和塔木德分配理论对上述案例的资源分配情况,计算得到具体分配情况见表7(不限定整数)。

表7 不同分配方法下各事故点对资源k1的分配量

从资源需求量上看,事故点N1对资源k1的需求量最大,可以认为该事故点受灾相对严重;N2的需求量最小,受灾相对较轻。从3种方式的分配结果可以看出,Shapley值分配法分配给受灾最严重的事故点N1的资源数量最多,其次是塔木德分配法,比例分配最少。该分配结果证明Shapley值分配法对受灾最为严重的事故点进行了重点考虑N1,充分反映了在救援初期资源不足的情况下,Shapley值分配方法的天平是倾向于弱者的。对于受灾程度相对较轻的事故点N2,资源分配数量最多的是比例分配法,其次是塔木德分配法,Shapley值分配法最少。3种分配方法分派给各个事故点的资源数量虽互有差异,但它们的变化范围处在同一数量级上,说明Shapley值分配法在优待弱者的同时,依然保证了博弈的公平性原则。

3种分配方法对资源k1的最优调度方案如表8。

表8 不同分配方法下资源k1的最优调度方案

将表8得出的最优调度方案代入式(4)和式(5),得到比例分配和塔木德分配对于资源k1的综合成本分别为105 804.7元和105 480.3元,而Shapley值分配法的综合成本为105 457.8元。由此可知,根据Shapley值分配原则进行资源分配调度时所产生的综合成本最小,能最大程度上减少事故造成的经济损失。

与比例分配原则相比,Shapley值分配原则基于公平分配理论,根据减少损失的程度对事故点所需资源进行分配,考虑每种分配方法所减少的边际损失,体现了“按劳分配”的原则,具有较强的合理性。相比于塔木德分配原则适用于应急资源较为充足的情况,Shapley值法分配原则在大规模铁路突发事件初期,应急资源储备量不足以满足所有事故点的需求量的情况下更为适用。

7 结 论

针对铁路突发事故初期多事故点多救援点的资源分配问题,通过综合分析现有的资源公平分配方式,采用Shapley值分配法对各需求点进行了资源分配,在此基础上以救援时间最短、资源运输成本最小为目标建立多目标优化模型,并借助Lingo软件求解,得到的结论如下:

1)将Shapley值分配原则用于铁路应急资源调度工作中,为大规模铁路突发事件下多事故点-多救援点-多种应急资源的资源调配提供了新的思路和方法。通过Shapley值计算结果来衡量各个事故点应急资源得到满足时所减少损失的程度,并以此计算各事故点进行资源分配的比例系数,这个过程既考虑了分配的效益,又兼顾分配的公平性原则。

2)将Shapley值分配方法对资源k1的分配结果与比例分配和塔木德分配方法的分配结果进行对比,结果表明Shapley值分配方法能更好地考虑受灾程度相对严重事故点。并且3种分配方法分派给各个事故点的资源数量虽互有差异,但它们的变化范围处在同一数量级上,说明Shapley值分配法在优待弱者的同时,依然保证了博弈的公平性原则。