宽浅式梯形渠道流速分布规律及流量计算方法研究

刘鸿涛，赵宇博，李晓军，龙昱帆，赵 虎，张福军

（1.长春工程学院水利与环境工程学院，长春 130012；2.吉林省水工程安全与灾害防治工程实验室，长春 130012；3.中水东北勘测设计研究有限责任公司，长春 130021；4.吉林省水利水电勘测设计研究院，长春 130021；5.永吉县星星哨水库灌区管理中心，吉林 吉林 132214）

0 引 言

我国现有大中型灌区7 800 多座，年均灌溉用水量2 150亿m3左右，占全国农业灌溉用水量的63%，是我国农业节水的主战场[1,2]。我国灌溉水有效利用系数仅为0.565[3,4]，精准测量明渠流量是节水工程建设的一个重要因素，同时也是一项迫切需要解决的灌区管理实际技术问题[5-7]。灌区管理人员通常采用“六点法”对大型干渠进行测流，对大型干渠来说，为满足渠道不冲流速和渠床稳定，常采用宽深比较大的渠道断面型式（宽浅式梯形断面），应用“六点法”进行测流虽然测流精度较高，但是测流历时较长，使用“六点法”测一个干渠断面通常都需要1 h 以上，效率较低，且不能获取瞬时流量。

目前对于明渠流速分布规律都源自于1904年Prandtl[8]提出的边界层理论，1938年Keulegan[9]将边界层理论引入到紊流的流速分布研究，提出明渠均匀流对数律流速分布公式；19世纪末学者们通过对大量明渠及管道试验，得到了纯理论的指数律流速分布公式；1956年Coles[10]提出了更符合实际流速分布的尾流函数；1985年Subrahmanyam Vedula[11]通过研究推出了一种适用于紊流流态的抛物线律流速分布公式；1989年Nezu[12]和Cardoso[13]首次提出了将水流沿水深分为内区和外区；本世纪初孙东坡[14,15]提到内区以壁面影响为主，在外区用二次抛物线分布能较好地拟合实际分布规律，但对公式形式及相应参数缺乏系统的研究。因此本文基于抛物线律流速分布公式，使用正交距离回归算法对数据进行曲线拟合，得出了宽浅式梯形渠道中心区与边壁区流速分布影响系数公式，得出了适合拟合宽浅式梯形渠道断面流速分布规律的方法；推导了中垂线单点测流方法及中垂线表面流量公式，对提高灌区测流效率具有一定的理论意义和应用价值。

1 材料与方法

1.1 研究区概况

对于常用的梯形渠道，按水力最佳断面设计的渠道断面往往是窄深式的。为此，应求一个宽浅式的梯形断面，使其水深和底宽有一个较广的选择范围以适应各种情况的需要，而在此范围内又能基本上满足水力最佳断面的要求，这种断面称为实用经济断面[8]。周春霞[16]通过《灌溉与排水工程设计规范》(GB 50288—99)来设计梯形干渠实用经济断面，根据计算结果表示，宽深比在1.49～4.49 之间的渠道为宽浅式的实用经济断面；闵志华[17]提出宽浅式灌溉渠道采用宽深比为2的横断面形式最为经济。综上，本文将宽深比大于2的梯形渠道定义为宽浅式梯形渠道。

本次试验分别在AB两地灌区进行，所选干渠断面形式均为剖面规则的宽浅式梯形断面，A地干渠底宽3.5 m，水深1 m，m=1.5，宽深比=3.5，为膜袋护坡；B地干渠底宽24 m，水深1.4 m，m=1.7，宽深比=17，为混凝土护坡。

1.2 试验装置与方法

（1）试验装置。试验采用德立达RD 仪器公司生产的声学多普勒剖面流速仪测量渠道流速及流量，其流速测量精度2.5 mm/s，流量误差为±0.25%，现场试验后通过WinRiver II 软件提取流速及流量数据。试验在室外进行，试验段水流保持为恒定均匀紊流，实测水温为11 ℃左右。

（2）试验方法。以测点距渠底距离h为横坐标，流速v为纵坐标建立宽浅式梯形渠道流速水深分布图，如图1所示，发现不同垂线上测点的流速大小与其在测线的相对位置具有密切的二次函数对应关系，经过大量分析及查询前人资料在此引入无量纲相对流速与相对水深进行量纲分析。

图1 宽浅式梯形渠道流速水深分布图Fig.1 Wide shallow trapezoidal channel velocity and water depth distribution diagram

相对水深为测点至渠底的距离与对应测线水深的比值，本文采用测点实际流速与平均流速之比作为相对流速[18]进行拟合，如式（1）所示。

式中：v为测点瞬时流速，m/s；va为测线平均流速，m/s；h为测点距渠底距离，m；H为测线水深，m；a、b、c为垂向流速分布影响系数。

宽浅式梯形渠道断面分区示意图如图2 所示。图中，d为测线至中垂线的距离，m；D为测线至边壁的距离，m；b为渠底宽度，m；B为水面宽度，m。

图2 宽浅式梯形渠道断面分区示意图Fig.2 Broad shallow trapezoidal channel section schematic diagram

2 结果与分析

2.1 宽浅式梯形渠道垂向流速分布规律

采用正交距离回归算法对实际流速与垂线平均流速之比为相对流速与相对水深进行曲线拟合。以A地干渠测桥断面边壁区第三条垂线为例，相对流速与相对水深关系见式（2）。式中vi为第i个测点的实际流速，hi为第i个测点距渠底距离。对式（3）取a、b、c的偏导数见式（4），联立求得第三条垂线的垂向流速分布影响系数为a=-0.396、b=0.723、c=0.777。

同理分别计算出中心区与边壁区每条测线垂向流速分布影响系数值，如图3和图4所示。

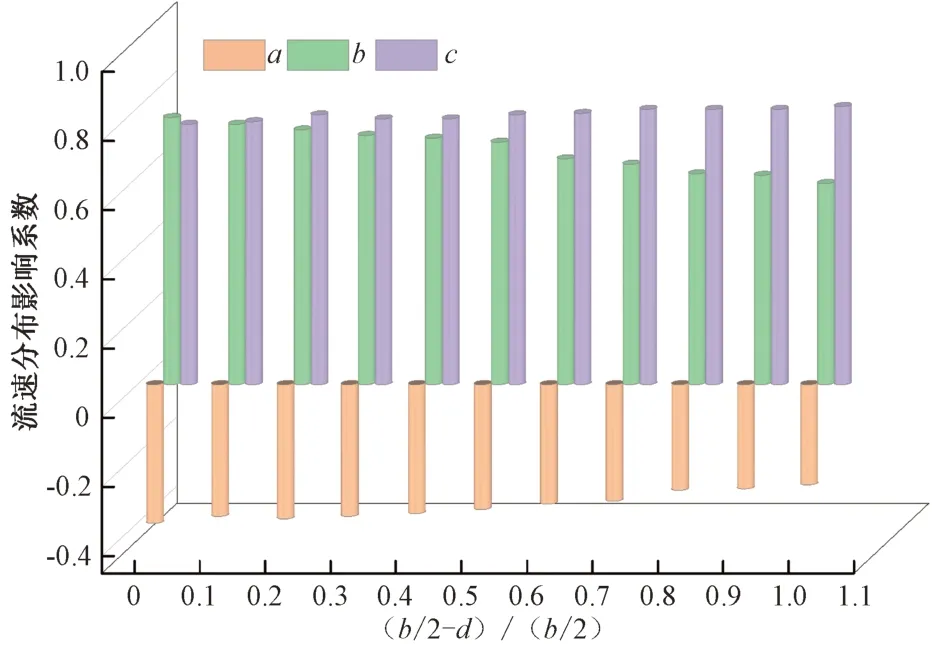
图3 宽浅式梯形渠道中心区垂向流速分布影响系数图Fig.3 Figure of influence coefficient of vertical velocity distribution in the center of wide shallow trapezoidal channel

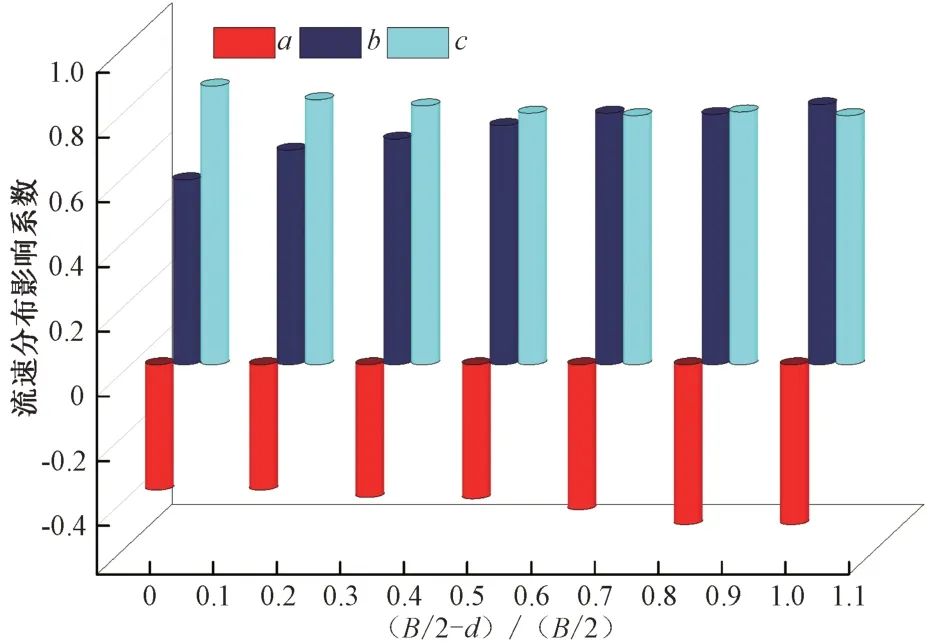
图4 宽浅式梯形渠道边壁区垂向流速分布影响系数图Fig.4 Figure of influence coefficient of vertical velocity distribution in side wall area of wide shallow trapezoidal channel

各测线垂向流速分布影响系数与其横向相对位置存在相关关系，进而对垂向流速分布影响系数与横向相对位置进行线性拟合，得出垂向流速分布影响系数随横向相对位置变化的函数公式。

在中心区:

中心区流速影响系数a、c随着与中垂线的距离的减小而增大，而系数b则相反。

在近壁区：

近壁区流速影响系数a、c随着与中垂线的距离的减小而减小，而系数b则相反。

使用正交距离回归算法对测点实际流速与平均流速之比作为相对流速和相对水深进行二次抛物线函数拟合，中心区各测线垂向相对流速与相对水深流速分布拟合如图5所示，近壁区各测线垂向相对流速与相对水深流速分布拟合如图6所示。

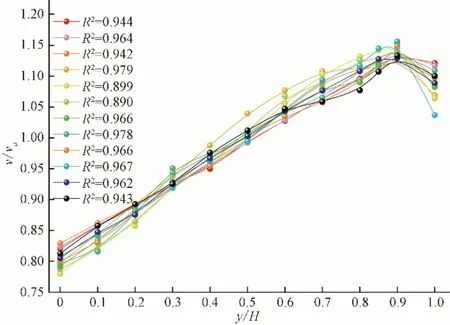
图5 宽浅式梯形渠道中心区各垂线垂向流速分布拟合图Fig.5 The fitting diagram of vertical velocity distribution of each vertical line in the center of wide shallow trapezoidal channel

图6 宽浅式梯形渠道边壁区各垂线垂向流速分布拟合图Fig.6 The fitting diagram of vertical velocity distribution of each vertical line in the side wall area of wide shallow trapezoidal channel

综上，近壁区与中心区垂向流速分布影响系数a、b、c的变化趋势明显不同，且垂向流速分布影响系数与其横向相对位置呈现一次函数关系。宽浅式梯形渠道中心存在流速稳定区，中垂线附近流速分布基本相同，使用实际流速与平均流速之比作为相对流速与相对水深进行拟合，拟合度大多数在0.937以上，可用于表示宽浅式梯形渠道垂线流速分布情况。

2.2 宽浅式梯形渠道横向流速分布规律

通过对前人流速分布资料及实测工程流速资料分析，宽浅式梯形渠道横向流速变化连续，且流速变化符合对称原则。相对流速与横向相对位置存在相关关系，将横断面相对流速与横向相对位置表示为式（11）。

式中：vi为第i条测线平均流速，m/s；vk为中垂线平均流速，m/s；p、q为横向流速影响系数。

宽浅式梯形渠道横向流速分布规律如图7 所示。从图7 中可以看出宽浅式梯形渠道横向流速分布在近壁区流速变化明显大于中心区，由于实测渠道数据有限，横向流速的验证只局限于边坡系数在1.5～2.0之间的宽浅式梯形明渠渠道。

图7 宽浅式梯形渠道横向流速分布规律图Fig.7 Distribution law of lateral velocity of wide shallow trapezoidal channel

通过对式（11）线性拟合分析，得到p=0.964～1.15，q=0.06～0.184，进一步对渠道流速数据对比分析得出横向流速影响系数p=0.988，q=0.112，并对其进行流速验证如图8所示。

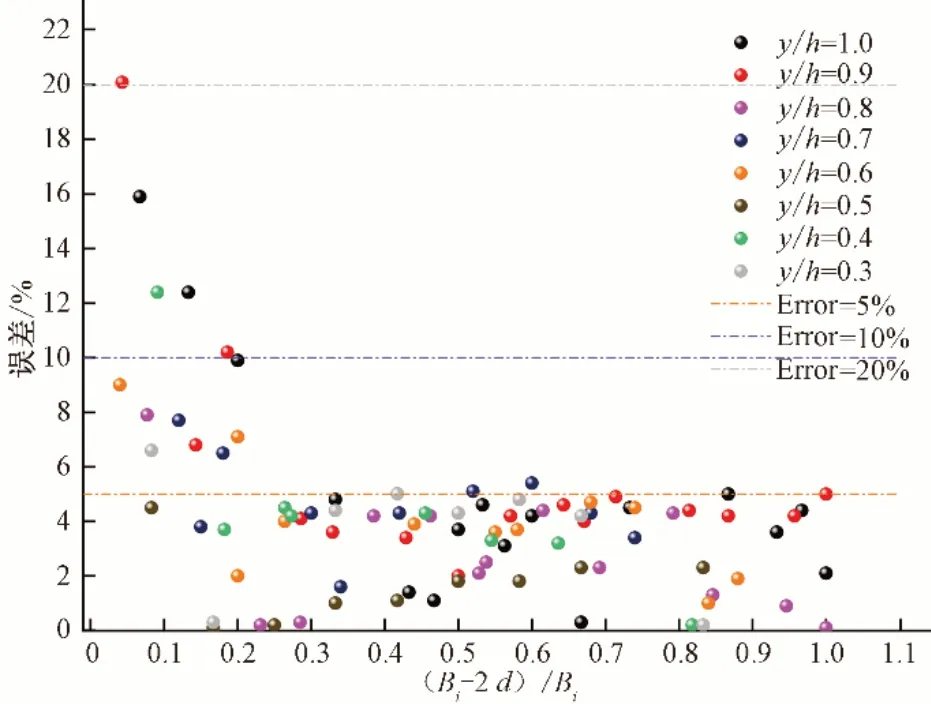
图8 宽浅式梯形渠道横向流速分布公式误差验证图Fig.8 Error verification diagram of lateral velocity distribution formula for wide shallow trapezoidal channel

从图8可以看出最大误差主要在出现在边壁区，在横向相对位置0.2<(B-2d)/B<1 区间内误差在5%范围内，靠近边壁区域公式的拟合度降低，计算存在较大误差，查阅相关资料，认为边壁区计算精度降低是与壁面剪切力对测点流速影响增大有关[19]。

2.3 宽浅式梯形渠道流量计算

很多灌区采用中垂线0.4 倍水深处流速代替渠道断面平均流速，这种单点测流法为工程经验得来，误差较大。笔者根据中垂线表面流速与断面平均流速关系提出一种新型便捷测流方式。将断面平均流速、中垂线平均流速va等条件带入断面中垂线垂向流速分布公式（12），反推得到断面平均流速值出现于中垂线0.36 h。以中垂线0.36 h 处流速作为断面平均流速与断面面积相乘求得断面计算流量见式（13）。

式中：为断面平均流速，m/s。Q为渠道计算流量，m³/s；v0.36h为中垂线0.36h处流速，m/s；A为断面面积，m2。

将中垂线表面流速h/H=1代入公式（12）求得中垂线表面流速为1.09倍中垂线平均流速，同理得断面平均流速h/H=0.36为0.975 倍中垂线平均流速，进而得到断面平均流速与中垂线表面流速关系式。

式中：vs为中垂线表面流速，m/s。

将渠道v0.36h作为断面平均流速与断面面积相乘求得断面计算流量，对AB两地干渠其他断面得出的计算流量与实测流量绘于图9 和图10 中，发现误差均小于5%，该计算公式可以用于灌区量水。

图9 A地干渠断面计算流量与实际流量误差图Fig.9 Error diagram between calculated flow and actual flow of ground trunk canal section A

通过该表面流速流量公式测量宽浅式梯形渠道干渠断面流量，将灌区常用的“六点法”变成测量中垂线表面流速的“一点法”，能够快速获取断面瞬时流量；为图像测流法、时空测流法等通过表面流速计算断面流量提供了计算公式与方法。

3 讨 论

为探求宽浅式梯形渠道的流速规律及测流方法，作者在AB两地灌区进行了大量试验。结果发现：在两条干渠断面流速分布中均存在流速稳定区，由于岸线附近水流受边壁影响导致靠近渠壁的流速较小，也就导致近壁区的平均流速沿横向变化较大，中心区则变化相对平稳，中心附近的垂向流速分布曲线极为相似，流速变化极小。

根据周和平[20]对水深小于1 m、水面宽度小于5 m 的不同类型渠道进行测量，应用经验法测量单点中垂线水深0.633 处流速，流量计算误差均在5%以内；本文通过对数据拟合得到的中垂线0.36 h 处流速（即水深0.64 处流速），同前人研究结果贴合，因此该方法同样适用于不同边坡、不同糙率（本文A地灌区为膜袋护坡，B地灌区为混凝土护坡）、不同断面类型的渠道。本文通过拟合得到的中垂线流速分布公式推导出断面平均流速与中垂线表面流速关系式，有利于简化渠道测量方法，对灌区量水有着积极的影响。

在后续的流量测量中发现，使用该单点测流法在对不同时刻、不同断面的宽浅式梯形渠道测流时，断面平均流速值在中垂线上的相对位置有较大波动，造成流量误差的增加，希望能够在单点测流的基础上，进一步研究断面平均流速与断面各测线表面流速之间的关系式，得到整个断面表面流速同断面平均流速之间的统一关系式，从而通过增加测线数量来降低流速波动造成的误差。

4 结论与展望

现阶段，灌区大型渠道常使用“六点法”测量断面流量，效率低且不能获取瞬时流量，本文针对实用经济型宽浅式梯形渠道，应用软件拟合分析采集的渠道断面点流速，得到了宽浅式梯形渠道中垂线单点测流公式和中垂线表面流速流量公式，可用于宽深比为3.7 和17、边坡系数在1.5～1.7 的宽浅式梯形渠道，并得出以下几点结论：

（1）使用测点实际流速与平均流速之比作为相对流速拟合得到的断面流速分布规律的R2均在0.937 以上，可用于表示宽浅式梯形渠道流速分布规律；分别得出了宽浅式梯形渠道中心区与边壁区流速分布影响系数计算公式，垂向流速分布影响系数与其横向相对位置呈现一次函数关系；分析得出宽浅式梯形渠道测线平均流速横向流速分布符合乘幂函数分布形式。

（2）应用渠道v0.36h作为断面平均流速，使用“流速～面积法”得到渠道计算流量，测流误差小于5%，满足《灌溉渠道系统量水规范GB/T 21303—2017》，可用于实际渠道的测量。

（3）通过待定系数法进一步得到了宽浅式梯形渠道断面平均流速与中垂线表面流速关系：-v= 0.893vs，有利于简化测流过程，提高测流效率。

（4）对于不同宽深比的流速分布是否不同和较大宽深比是否与矩形渠道流速分布类似，还需要做进一步的研究。