An efficient wear-leveling-aware multi-grained allocator for persistent memory file systems*&

Zhiwang YU ,Runyu ZHANG ,Chaoshu YANG ,Shun NIE ,Duo LIU

1State Key Laboratory of Public Big Data, College of Computer Science and Technology,Guizhou University, Guiyang 550000, China

2College of Computer Science, Chongqing University, Chongqing 404100, China

Abstract: Persistent memory (PM) file systems have been developed to achieve high performance by exploiting the advanced features of PMs,including nonvolatility,byte addressability,and dynamic random access memory(DRAM)like performance.Unfortunately,these PMs suffer from limited write endurance.Existing space management strategies of PM file systems can induce a severely unbalanced wear problem,which can damage the underlying PMs quickly.In this paper,we propose a Wear-leveling-aware Multi-grained Allocator,called WMAlloc,to achieve the wear leveling of PMs while improving the performance of file systems.WMAlloc adopts multiple min-heaps to manage the unused space of PMs.Each heap represents an allocation granularity.Then,WMAlloc allocates less-worn blocks from the corresponding min-heap for allocation requests.Moreover,to avoid recursive split and inefficient heap locations in WMAlloc,we further propose a bitmap-based multi-heap tree (BMT) to enhance WMAlloc,namely,WMAlloc-BMT.We implement WMAlloc and WMAlloc-BMT in the Linux kernel based on NOVA,a typical PM file system.Experimental results show that,compared with the original NOVA and dynamic wear-aware range management (DWARM),which is the state-of-the-art wear-leveling-aware allocator of PM file systems,WMAlloc can,respectively,achieve 4.11× and 1.81× maximum write number reduction and 1.02× and 1.64× performance with four workloads on average.Furthermore,WMAlloc-BMT outperforms WMAlloc with 1.08× performance and achieves 1.17× maximum write number reduction with four workloads on average.

Key words: File system;Persistent memory;Wear-leveling;Multi-grained allocator

1 Introduction

Emerging persistent memories (PMs),such as phase change memory (PCM) (Palangappa et al.,2016) and 3D XPoint (Intel,2015),have promised to revolutionize storage systems by providing nonvolatility,byte addressability,and low latency,which can be directly linked to the memory bus and accessed through central processing unit (CPU)load/store instructions (Condit et al.,2009).In recent years,many PM file systems,such as PMFS(Dulloor et al.,2014),SIMFS (Sha et al.,2016),NOVA (Xu and Swanson,2016),HiNFS (Ou et al.,2016),and SplitFS(Kadekodi et al.,2019),have been developed to achieve high performance by exploiting the advanced features of PMs.

Unfortunately,PMs have the problem of limited write endurance (Huang FT et al.,2017;Liu et al.,2017;Chen et al.,2018;Yang et al.,2020b).However,existing PM file systems aim to further improve the performance rather than achieving wearleveling of underlying PMs.Accordingly,the existing space management strategies of PM file systems can easily cause “hot spots;” i.e.,the write operations are usually concentrated on a few cells of the PMs,which can damage the underlying PMs quickly and seriously threaten the data reliability of PM file systems.Therefore,avoiding the wearout problem is a fundamental challenge for the design of allocators in PM file systems.

Recently,wear-leveling-aware allocators were proposed to improve the life span of PM for PM file systems.However,they focus mainly on improving wear accuracy rather than alleviating overhead for achieving wear-leveling of PM and support only single-grained allocation/deallocation for space management.Hence,existing wear-leveling-aware allocators can significantly reduce the performance of PM file systems.Therefore,it is critical to design an allocator that considers both high performance and high-accuracy wear-leveling of PM for PM file systems.

In this paper,we propose a Wear-leveling-aware Multi-grained Allocator,called WMAlloc,to solve these problems.The main idea of WMAlloc is to adopt a spatial management strategy between allocation and deallocation to achieve wear-leveling of PM while improving the performance of PM file systems.WMAlloc consists of three key techniques,namely,multi-grained allocating heaps(MGAH),wear-aware recycle forest(WARF),and wear-balancing node migration (WBNM),which are used to improve the performance of allocation,improve the performance of deallocation,and achieve high-accuracy wearleveling of PM,respectively (Nie et al.,2020).Furthermore,we propose a bitmap-based multi-heap tree (BMT) to mitigate the comprehensive redundant overhead of WMAlloc.

We implement WMAlloc and WMAlloc-BMT in the Linux kernel based on NOVA(Xu and Swanson,2016).The experimental results show that,compared with the original NOVA and dynamic wearaware range management (DWARM) (Wu et al.,2018) strategies,WMAlloc can reduce the performance overhead and achieve high-accuracy wearleveling of PM.Compared with NOVA,WMAlloc can achieve 4.11× lifetime of PM on average,and it gains similar performance.Compared with DWARM,WMAlloc can achieve 1.81× lifetime of PM and 1.64× performance on average.Moreover,WMAlloc-BMT outperforms WMAlloc with 1.08×performance and achieves 1.17× maximum write number reduction on average.Our main contributions are as follows:

1.We conduct in-depth investigations to reveal the severely unbalanced writes and the high overhead of existing wear-leveling-aware allocators of PM file systems.

2.We design an efficient WMAlloc using minheaps and red-black(RB)trees.WMAlloc can significantly reduce the performance overhead and achieve superior wear-leveling of PM for PM file systems.

3.We propose BMT to further improve the performance of WMAlloc.BMT refines the granularity of min-heaps to relieve fragmentation problems and mitigates considerable redundant overhead of WMAlloc.

4.Extensive experiments with various widely used workloads are conducted to evaluate the proposed mechanisms.Experimental results show that our solutions outperform existing schemes in terms of both performance and wear-leveling.

2 Background and motivation

2.1 PM file systems

Emerging PM file systems,such as PMFS(Dulloor et al.,2014),SIMFS (Sha et al.,2016),NOVA(Xu and Swanson,2016),HiNFS (Ou et al.,2016),and SplitFS (Kadekodi et al.,2019),exploit the advanced characteristics of PMs to avoid overhead of block-oriented input/output (I/O) stacks and thereby achieve higher performance than conventional block-based file systems.However,PMs suffer from limited write endurance;e.g.,a PCM cell can sustain only about 108writes (Chen et al.,2018;Gogte et al.,2019),which can seriously threaten the data reliability of PM file systems.Unfortunately,as the fundamental infrastructure that manages PM for storage systems,existing PM file systems usually ignore the critical problem of limited write endurance in PM.For example,existing space management strategies of PM file systems easily cause “hot spots,” which can lead to seriously unbalanced wear of PM.

To further improve the performance,existing PM file systems,such as PMFS(Dulloor et al.,2014)and NOVA (Xu and Swanson,2016),adopt multigrained allocators for space management.Briefly,file systems can allocate various block sizes in a single allocation.Current PM file systems use linked lists to manage used/unused blocks.Generally,there are two strategies of allocations on the lists.Circular allocations can induce severe fragmentation problems,especially for aging file systems.On the contrary,although always allocating from the head of lists can mitigate fragmentation problems,this strategy can lead to the writes being concentrated on the mostworn area.Accordingly,avoiding wear-out problems of PM is the fundamental challenge in the design of allocators for PM file systems.

2.2 PM wear-management schemes

Existing PM wear-management techniques usually adopt wear-leveling mechanisms (Hakert et al.,2020;Huang JC et al.,2022)to improve the lifetime of PMs,which spread writes uniformly over all PM memory locations to achieve balanced wear of underlying PM.Start-Gap(Qureshi et al.,2009),Security Refresh(Seong et al.,2011),Online Attach Detection(Qureshi et al.,2011),and ScurityRBSG(Huang FT et al.,2016)remap the cache lines in the hardware for uniform intra-page wear.All of these wear-leveling mechanisms require an additional indirection layer in the hardware to spread the writes to all PM cells,which can lead to massive data migration and redundant writes to PM cells,thereby incurring storage overhead and increasing access latency(Gogte et al.,2019).

Several recent arts,such as NVMalloc (Moraru et al.,2013),Walloc (Yu et al.,2015),UWLalloc(Li et al.,2019),and Kevlar (Gogte et al.,2019),have been proposed to optimize memory space management strategies in the operating system.These mechanisms achieve wear-leveling by always allocating low-worn pages and dynamically migrating hot data into low-worn pages to spread writes uniformly over all the PM memory space.However,these mechanisms are designed for the main memory architecture(e.g.,PM is used as the main memory or PM+DRAM as the hybrid main memory).Hence,they are still unfriendly to file systems since they are unaware of the special I/O characteristics of PM file systems (Yang et al.,2020a).

2.3 Wear-leveling-aware allocators of file systems

Existing space management strategies of PM file systems can easily cause unbalanced wear of underlying PM.Wear-leveling-aware allocators of PM file systems,such as DWARM (Wu et al.,2018),have been proposed to achieve wear-leveling of the underlying PM for further improving its lifetime.Unfortunately,these emerging wear-leveling-aware allocators focus mainly on evenly distributing wear while producing heavy overhead of achieving wear-leveling of PM.Consequently,they can seriously reduce the performance of PM file systems.

According to the worn counter of each page,as shown in Fig.1,DWARM divides all unused pages into groups.Moreover,all pages of a group are linked one by one via a single linked list.Furthermore,DWARM adopts the adaptive wear range determination algorithm to adjust the wear ranges of groups dynamically.Hence,DWARM achieves wear-leveling of underlying PM by allocating a page from the least-worn group for each allocation request.However,the wear accuracy of DWARM is closely related to its set range of groups.The larger group range brings lower wear accuracy of achieving wear-leveling.Conversely,the smaller group range provides superior wear-leveling and higher complexity of metadata management.

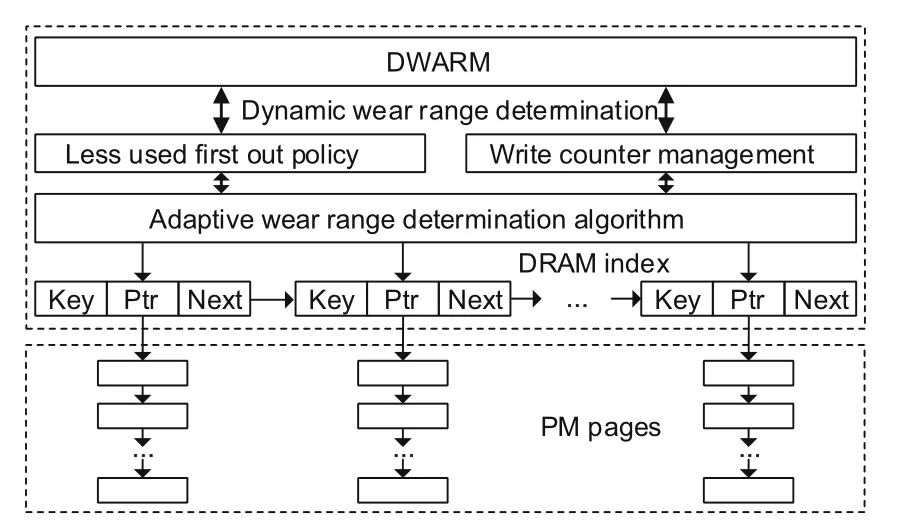
Fig.1 Logical overview of DWARM

Based on the above analysis,DWARM is only a single-grained allocator;i.e.,DWARM needs more rounds of allocations for allocating ＞1 page from the least-worn group.For example,when file systems need to allocate 512 pages,DWARM needs to conduct allocations 512 times.Comparatively,the multi-grained allocator may need only one round to complete the allocation request.Furthermore,each allocation operation is associated with a log operation.Therefore,compared with the multi-grained allocator,DWARM can cause higher performance overhead for space management during both allocation and deallocation,especially for those file systems that need to provide strong data consistency.

3 WMAlloc design

In this section,we first present the design overview of WMAlloc.Second,we introduce the construction of MGAH,which provides multi-grained allocations,and WARF,which achieves wear-leveling among pages.Finally,we introduce WBNM mechanism to solve imbalanced allocation among heaps.

3.1 Overview

WMAlloc consists of three key techniques.First of all,to support multi-grained allocation,we use multiple min-heaps to organize free blocks,similar to the buddy system.A node in the heaps records those blocks with a fixed number of contiguous pages.For each heap,the above number is different for variousgrained allocations.To record the wear degree of each page,we assign a space after the superblock of the file system to store the number of writes of each page.Each heap node stores a key to represent the average write counter of its consecutive pages.When we obtain a node with the minimum key in a min-heap,the blocks with lower write counters can thereby be allocated.

Second,for the released blocks,we construct a WARF to record them according to their wear degrees.The forest consists of multiple RB trees,each of which contains blocks with similar wear degrees.Contiguous pages are compacted as a block node in trees,akin to those of min-heaps.Newly released blocks are inserted into the corresponding tree and combined with their neighbor blocks.When the total number of blocks in the min-heaps is smaller than a threshold,we move a portion of the blocks in the forest to the min-heaps for future allocations.

Finally,for extreme cases,the blocks in some heaps are never allocated and uneven wear can be induced.Therefore,we propose a migration mechanism among min-heaps.Fig.2 shows the high-level layout of WMAlloc.

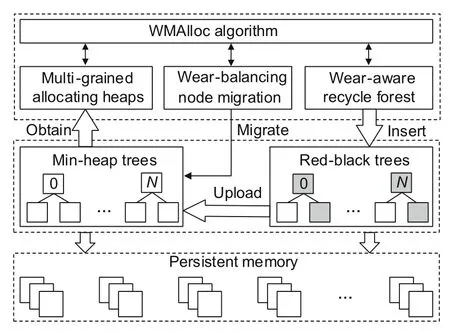
Fig.2 The overview architecture of WMAlloc

3.2 Multi-grained allocating heaps

As shown in Fig.3,we propose the MGAH mechanism to meet the requirements of multigrained allocation.First,we construct 11 min-heaps,numbered from 0 to 10.Theithmin-heap contains several nodes,each of which records contiguous 2ipages.For ease of description,we define the number of contiguous pages in a node as the granularity.The granularity of the 0thmin-heap is 1.The granularity of the 9thmin-heap is 29.All nodes with a granularity that is ＞29will be stored in the last min-heap(i.e.,the 10thmin-heap).To quickly locate the corresponding min-heap,we assign an array to store the root of each min-heap.

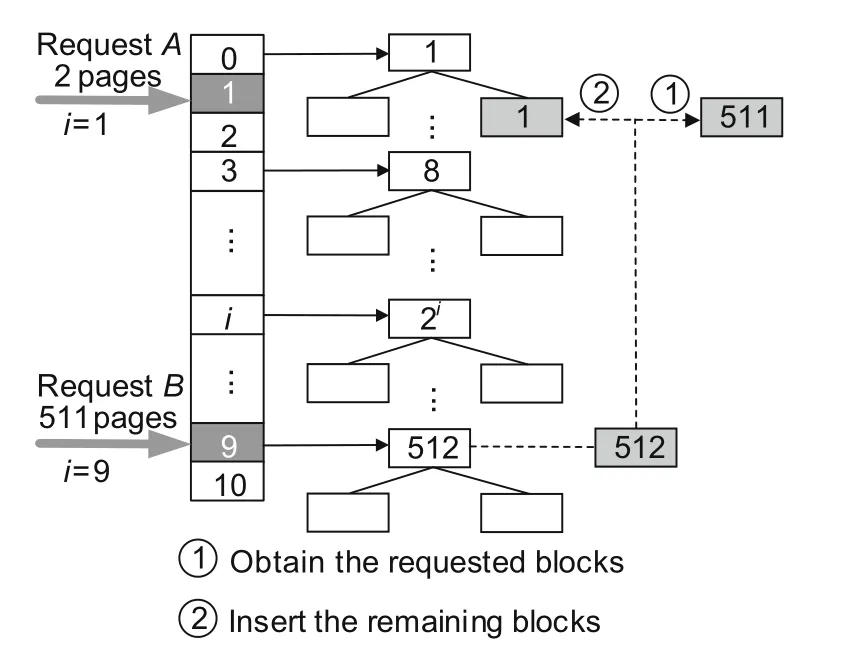
Fig.3 Allocation from multiple min-heaps

Algorithm 1 shows how to allocate blocks from the min-heaps.When allocatingPpages,WMAlloc first locates the root node in position「log2and returns the required pages.If the current minheap lacks enough pages,WMAlloc traverses from the next min-heap to the last one.If it still fails to allocate the required pages,WMAlloc reverses the search direction from position「log2-1 to the first heap.Note that to allocate fewer pages than what a node contains,WMAlloc inserts the remaining pages to the corresponding heap.Fig.3 illustrates the above cases.When allocating a block with two pages,WMAlloc directly locates min-heap 1 to obtain the required block.When allocating 511 pages,WMAlloc accesses min-heap 9 to take out a large block with 512 pages.Then,as in step ①,WMAlloc splits a 511-page block to satisfy the allocation.The remaining block with one page is inserted back into min-heap 0,as in step ②.

The min-heaps satisfy the needs for multigrained allocations.However,problems on replenishing the nodes to the min-heaps and on how to balance the wear degrees remain.In the next subsection,we introduce WARF,which uses multiple RB trees to solve these problems.

3.3 Wear-aware recycle forest

We construct a wear-aware recycle forest(WARF) to record the released blocks.The forest consists ofRRB trees.We create a loop array to store theirRroots.Each tree holds a threshold to record its maximum write counter.The threshold of the latter RB tree is always greater than that of the previous one.The nodes in an RB tree record the contiguous pages with similar wear degrees.The threshold is dynamically determined by the write counter of the pages within the tree.The number of nodes and the threshold of each tree are initialized to zero.

As shown in Fig.4,WMAlloc records the positions of the head and tail to locate the first and last roots of in-use RB trees,respectively.When a block is released,it is inserted into the corresponding tree according to its number of writes(denoted as writeCounter).WMAlloc finds the first tree whose threshold is equal to or larger than writeCounter via binary search.If no threshold is larger than write-Counter,WMAlloc directly inserts the block into the tail and moves the tail to the next tree.Then,the threshold of the tail is set as writeCounter.Otherwise,if the target tree is found,we calculateβ(previous_threshold+current_threshold) and compare the result with writeCounter.If the result is smaller than writeCounter,we insert the block to the current tree(Fig.4a).If writeCounter is smaller,which means that a huge gap exists between the current threshold and writeCounter,WMAlloc moves the larger roots including the current one to their next position and inserts the block via the current root(Fig.4b).Then,WMAlloc sets the threshold of the current one as writeCounter.This strategy automatically adjusts the threshold gap between two adjacent trees.Algorithm 2 shows the detailed steps of inserting a block into the RB tree.

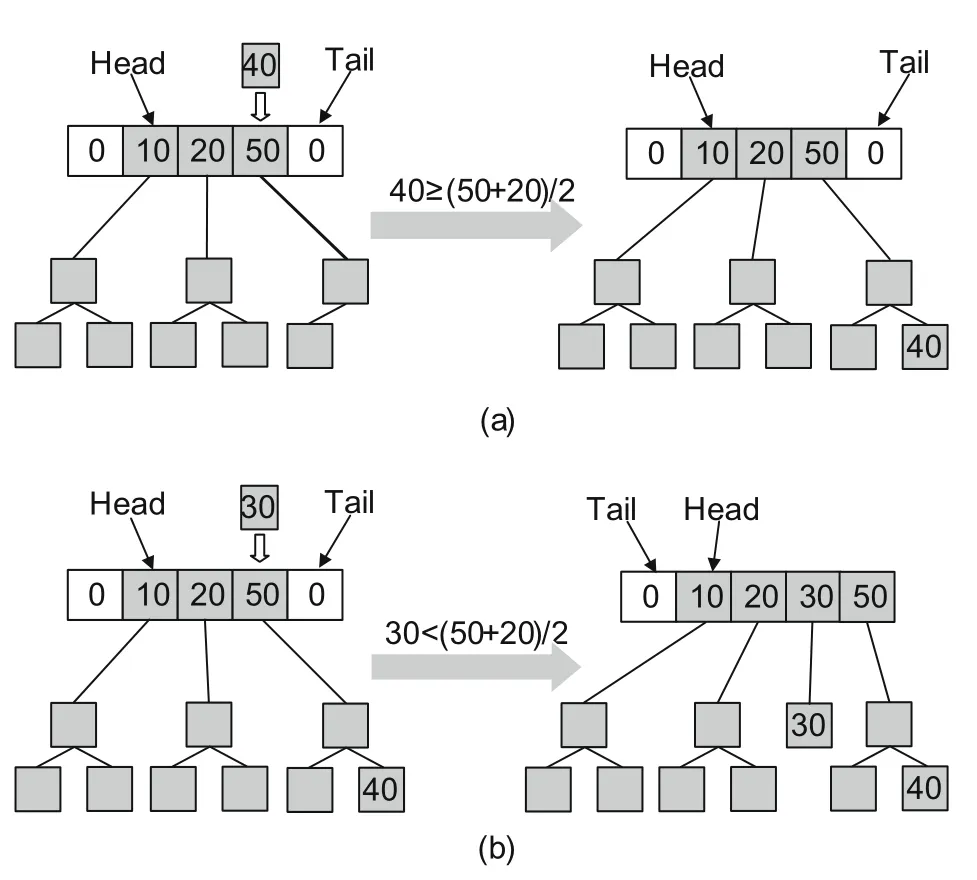
Fig.4 Inserting a released block into a red-black tree:(a) inserting a block with 40 writes;(b) inserting a block with 30 writes

When the number of blocks in the min-heaps is less thanα·total_free_blocks,WMAlloc migrates a part of the blocks from the RB tree to min-heaps.WMAlloc first obtains the nodes in the previousε(tail–head) RB trees.Then,it inserts these nodes into the min-heaps.If the workload always allocates blocks at the same granularity,these blocks can be severely worn,while others are less worn.To address this problem,we need to exchange the nodes with far different wear degrees among min-heaps.In the next subsection,we introduce the WBNM mechanism to resolve this problem.

3.4 Wear-balancing node migration

The basic idea of WBNM is to exchange the node in the least-worn min-heap with that in the most-worn min-heap and balance the uneven wear between min-heaps.We first propose a mathematical model to evaluate the wear degree of a min-heap.In Eq.(1),xrepresents the average writeCounter in this heap.We denotesas the standard deviation,which is used to represent the wear dispersion of all nodes in the min-heap.

Eq.(2) is one of the most commonly used data standardization methods,namely,theZ-score standardization method.It can be used to indicate the wear deviation of each node in the same heap.Ifzi ＞0,the wear degree of this node is determined as large,and vice versa.

The wear difference of nodes in a min-heap may vary greatly.To improve the wear accuracy and reduce the overhead,WBNM needs only to migrate the nodes with large wear in the most-worn min-heap to the least-worn min-heap,and the nodes with small wear in the least-worn min-heap to the most-worn min-heap.Therefore,the wear degree of a min-heap should be determined by the nodes with large wear or the nodes with small wear.WBNM calculates the averageZ-score of the nodes whoseZ-score value is larger than 0 in a heap,then adds it to 1,and multiplies it by the average wear degree of the heap;its result represents the overall wear degree wearlevel of the heap.The wearlevel can be calculated using Eq.(3),wherenis the total number of nodes in a min-heap andmis the number of nodes with less wear than the average value:

After calculating the wear degrees of the minheaps,the min-heaps with the most and the least wear (denoted asAandB,respectively) can be found.Then,we collect the nodes with larger wear than the average value inAand the nodes with smaller wear than the average value inB.Finally,we exchange these nodes for wear-leveling.Note that to control the overhead of calculations,an allocation counter Num_alloc is recorded for all heaps to count the number of their allocations.Only when a heap is allocated forσ·Num_alloc times,will the wearlevel of each heap be calculated.

For the migration process,if the granularity ofBis larger than that ofA,we decompose the nodes inBinto small-grained nodes and insert them intoA.Otherwise,we need to compact the smaller nodes into the larger granularity and conduct the migration.Note that to reduce the overhead of migration and loss of balancing accuracy,only the most-and least-worn nodes will be migrated.In other words,the nodes whose wear degrees are within the two average values will remain in the original heaps.

4 Bitmap-based multi-heap tree

4.1 Fine-grained multiple heaps

WMAlloc uses MGAH to efficiently conduct multi-grained allocations withO(1) complexity.However,it may suffer from redundant overhead when migrating blocks from the RB trees to the minheaps or allocating from blocks with greater granularity than required.To be specific,in MGAH,heapimanages blocks with 2ipages.For example,when migrating a block with 511 pages,WMAlloc splits it into nine sub-blocks containing 256,128,64,32,16,8,4,2,and 1 page(s),separately,and inserts them into the min-heaps one by one.Similarly,when allocating 200 pages from a block with 711 pages,it splits the remaining block into nine sub-blocks and conducts the above insertions.

This mechanism can cause performance drop from two aspects.First,large blocks are split into several discrete small blocks,leading to scarce large blocks for future allocations.As a consequence,it needs to allocate several small blocks for large allocation requests.To make things worse,since each allocation must log in the journaling area,massive small allocations severely degrade the system performance and endurance of the journaling area.Second,to ensure wear-leveling accuracy,in the process of splitting of blocks,the average write counter of each sub-block needs to be recalculated.In other words,every split operation triggers an iteration on all write counters of pages within this sub-block,introducing considerable overhead and unpredictable long tail latency.

To avoid these redundant splits,we propose BMT to substitute the original MGAH.The basic idea of BMT is to refine the granularity of minheaps to accommodate the remaining sub-blocks and cut offthe recursive split.In BMT,we expand the number of min-heaps to 512.Theithmin-heap contains blocks withi+1 pages,rather than 2ipages in MGAH.All blocks with≥511 pages are recorded in the last min-heap.Based on this design,the migrated blocks in every granularity can be assigned into the corresponding min-heap inO(1) without splits.Although allocating from a large block may still produce a split operation,the remaining subblock will be directly inserted into the corresponding min-heap without further splits.

4.2 Bitmap-based indexing structure

If the targeting min-heap is empty,WMAlloc needs to traverse the following min-heaps for allocations.To address this inefficient locating,we construct a bitmap-based index to quickly indicate the information of min-heaps.As shown in Fig.5a,there are three levels of bitmaps above the 512 min-heaps.The top-level bitmap is a byte-sized integer,while the middle-and bottom-level bitmaps occupy 8 and 64 bytes,respectively.Theithbit in the 64-byte(512-bit) bottom-level bitmap indicates the availability of theithmin-heap.Specifically,if theithmin-heap is empty,the correspondingithbit will be zero;otherwise,it will be one.

Fig.5 An example of searching the candidate min-heap: (a) original bitmap-based multi-heap;(b) allocating a block with two consecutive pages;(c) allocating a block with six consecutive pages;(d) allocating a block with 38 consecutive pages

Above every eight bottom-level bitmaps,there is a middle-level bitmap to indicate their availability.If a bit in a middle-level bitmap is zero,its corresponding bottom-level bitmap is also zero.This means that the corresponding eight min-heaps are all supposed to be empty.Otherwise,the corresponding bottom-level bitmap is not totally zero.There should be at least one available min-heap underneath the corresponding bottom-level bitmap.Similarly,we construct the top-level bitmap,using one byte to indicate the availability of the whole free space.If a top-level bit is zero,the corresponding middle-level bitmap and eight bottom-level bitmaps are zero,and vice versa.

For ease of storage and indexing,we record the above three levels of bitmaps in an integer array bmp.The first 0thto 63rdbytes of the bmp are occupied by the bottom-level bitmaps.Subsequently,the 64thto the 71stbytes of the bmp record the middle-level bitmaps.Finally,the 72ndbyte is the top-level bitmap.Benefiting from the bitmap-based indexing structure,it is possible to quickly locate the available fine-grained min-heap with the minimum maintenance cost.In the following subsection,we detail the operations on BMT.

4.3 BMT operations

4.3.1 Block insertions

Initially,the values of all bitmaps are zero since there is no free block in the min-heaps.When the free blocks migrate from the RB trees,they are inserted into the corresponding min-heaps.Once theithempty min-heap turns to an available one,the(i%8)thbit of the (i/8)thbyte in bmp will be set to one.If the (i/8)thbyte in the bmp is zero before this insertion,which means that its corresponding middle-level bit is zero,we also need to turn the middle-level bit to one.Denoting the bottom-level byte blb=i/8,the corresponding middle-level byte slb=64+blb/8.We turn the (blb%8)thbit of the slbthbyte in bmp to one.Likewise,if the slbthbyte of the bmp is zero before this insertion,we modify the top-level bitmap (i.e.,the (slb%8)thbit of the 72ndbyte)to one.

4.3.2 Block deletions

The allocated free block should be deleted from its min-heap.Block deletions are basically the opposite of insertions.When the last free block in theithmin-heap is allocated,we turn the(i%8)thbit of the(i/8)thbyte in bmp to zero.Then,we check whether the value of the(i/8)thbyte is zero or not.If it is zero,we need to modify its corresponding middle-level bit to zero,akin to insertion operations,and conduct another value check to decide whether we need to further modify the top-level bitmap.Note that if the modified byte has already been one before the block insertions or is still one after deletions,there is no need to manipulate the upper-level bitmaps.Besides,since BMT has only three levels,the number of bitwise modifications is constrained by three in the worst case.Therefore,the maintenance overhead of BMT is controllable and acceptable.

4.3.3 Quickly locating available min-heaps

With minimized maintenance overhead,WMAlloc gains great performance benefits on probing available min-heaps.When an allocation request encounters an empty min-heap,it needs to find the next available min-heap with a minimum granularity that is just greater than the requested one.Facilitated by BMT,we are able to quickly locate the qualified min-heap without traverses.

As illustrated in Algorithm 3,with a given granularityP,we first access the corresponding min-heapN=P-1 and check whether it is empty or not.If this min-heap is empty,we check the nearest eight min-heaps via the bottom-level bitmap bmp[N/8].Denoting the byte-sized bitmapB=bmp[N/8],we conductB ＞＞(N%8) to shift out the min-heaps with smaller granularities.Then,we can obtain its lowest 1 bit by calculatingB&(-B).To map the serial number of the lowest 1,we construct a mapping tablemin advance.This mapping table has 27+1 integers andm[2i]is set toiinitially.In this way,we can directly obtain the serial number of the lowest 1 bym[B&(-B)].Provided thatB≠0,we can accomplish this allocation at the min-heap with serial numberN+m[B&(-B)].

Otherwise,onceN/8≠63 (which means thatBis not the last bottom-level bitmap),we need to expand our search scope to the nearest 64 minheaps via the middle-level bitmap.Since the nearest eight min-heaps have been proved not proper,we letp=N/8+1 to search from the next eight min-heaps.The middle-level bitmap can be located byB=bmp[64 +p/8].Similar to bottom-level search,we right-shift the bitmapBbyp%8 and calculateB&(-B) to know whether an available min-heap exists under this middle-level bitmap.If so,we conduct another bottom-level search on bytep+m[B&(-B)] to further check the location of the targeting min-heap.Otherwise,there is no available min-heap nearby.In this case,onceN/64≠7 (which means that there are still unsearched middle-level bitmaps),we have to search the top-level bitmap(i.e.,B=bmp[72]) to roughly locate the targeting area.We denoteq=p/8+1 and right-shiftBbyq%8.IfB≠0,we turn to conduct a middle-level search on byteq+m[B&(-B)].Otherwise,there is no proper min-heap and the request cannot be accomplished by one allocation.

Fig.5 illustrates three examples of fast locations.To facilitate understanding,we still demonstrate the bitmap in a tree style.When allocating a block with two consecutive pages,as shown in Fig.5b,we first access min-heap 1 to seek free blocks.Unfortunately,this min-heap is empty(since its corresponding bit is zero);we need to probe the nearest eight min-heaps (from 0thto 7thbits).We right-shift the first byte of the bottom-level bitmapBby(2-1)%8=1 and calculateB&(-B)to obtain a result 0x0001000.From the mapping tablem,we know that the serial number of its lowest 1 bit is 3.Finally,we find the targeting min-heap by 1+3=4.

A more complicated situation exists in Fig.5c.It fails to allocate a block with six consecutive pages underneath the first bottom-level bitmap.Therefore,we turn to search the nearest 64 min-heaps via the corresponding middle-level bitmap.After similar calculations,we find that the fourth bit of the middle-level bitmap hints that there will be available min-heaps.We further exploit the fourth byte of the bottom-level bitmap and finally locate the proper min-heap with serial number 34.

Fig.5d presents the worst case of heap locations.It cannot find a feasible min-heap in both the bottom-and middle-level probes.Hence,we check the top-level bitmap and find the nearest one in the second bit.Then,we search down the corresponding middle-level bitmap to locate the targeting bottomlevel bitmap.Through the guidance of the third bit in the second middle-level bitmap(serial number 19),we enter the 19thbottom-level bitmap.Finally,we locate the proper min-heap 154.

From the above examples,we can observe that it needs only a few bitmap calculations to locate a proper min-heap.The maximum number of calculations is only five even in the worst case.Therefore,the overhead of min-heap locations is extremely mitigated compared with massive traverses.

4.3.4 Conditional wear inheritance

In addition to the search of available min-heaps,calculating the average wears of the split blocks accounts for a large portion of redundant overhead.Hence,we propose a conditional wear inheritance mechanism to mitigate the overhead while guaranteeing decent wear accuracy.When the selected minheap has a greater granularity than the requested one,the allocated block will be split into two subblocks.We denote the size of the original block asT,the requested size asP,and a ratioγas a threshold.We useP/Tto represent the potential wear fluctuation caused by the allocation request.IfP/T ≤γ,we consider that the average wear of the victim block will not fluctuate violently.Hence,we directly inherit the wear degree of the original block to the remaining block.As a consequence,the recalculation is eliminated.However,ifP/T ＞γ,the remaining block takes up only a small portion of the original one.In this case,it is necessary to recount the average wear of the remaining block.Though,the performance overhead is significantly limited since the size of the remaining block is smaller than that of the allocated block.

5 Evaluation

5.1 Experimental setup

We implement a prototype of WMAlloc,WMAlloc-BMT,and DWARM (Wu et al.,2018)on Linux kernel 5.1.0 and integrate them into NOVA(Xu and Swanson,2016).WMAlloc and WMAlloc-BMT are compared with the original NOVA and DWARM.The experiments are conducted on a machine equipped with two 26-core 2.20 GHz Intel Xeon®Gold 5320 processors,8×32 GB DRAM,and 8×128 GB Optane DC PM module.We mount NOVA,DWARM,WMAlloc,and WMAlloc-BMT on 256 GB pmem0 device using APP Direct Mode.

The configuration is as follows.For DWARM,the threshold of splitting the index list and temp list is set to 25%.For WMAlloc,the thresholds of migrating blocks from the RB tree to min-heaps and moving root when inserting a block to the RB tree are set as 10%(i.e.,α)and 50%(i.e.,β),respectively.WMAlloc obtains the nodes in the previous 10%RB trees when migrating nodes to min-heaps.Meanwhile,the threshold of WBNM is set as 80%(i.e.,σ).The wear fluctuation threshold of WMAlloc-BMT is set as 50%(i.e.,γ).

In the experiments,we first use a widely used benchmark,createdelete-swing of filebench(Tarasov et al.,2016) and fio,as the micro-benchmark,and two typical workloads,fileserver of filebench and postmark (Network Appliance,Inc.,2022),as macro-workloads,to analyze the write distribution of NOVA,DWARM,WMAlloc,and WMAlloc-BMT.Then,we use these four workloads to evaluate their overall performance.

The fio is a widely used benchmark for performance evaluations of file systems;it can generate and measure a variety of file operations.The createdelete-swing function continuously creates files,then deletes them,then creates them again,and so on,until the time is up.The fileserver performs a sequence of create,write,append,and delete operations on a directory tree,resulting in continual allocation of new free space,leading to a broad access section.The postmark workload is designed to create a large pool of continually changing files and to measure the transaction rates for a workload approximating a large Internet e-mail server.

The detailed configuration of the four workloads is as follows.In fio tests,we write to an existing 200 GB file using one thread (i.e.,sequential write).The mean width of the directory is set as 10 000 in createdelete-swing.Meanwhile,the mean file size and mean append size are set as 256 KB and 128 KB in fileserver tests,respectively.For both createdelete-swing and fileserver tests,the running time is set as 1800 s,and the total count of files is set as 100 000,200 000,and 400 000,separately.For postmark tests,the transactions are set as 2 000 000,the file size ranges from 1 KB to 4 MB,the writeand-read block size is set as 64 KB,and by default,the total count of files is 10 000,20 000,and 40 000,separately.

5.2 Impact on lifetime of PM

To obtain the write distribution of all PM pages,we add codes into NOVA,DWARM,WMAlloc,and WMAlloc-BMT to track the write counter of each page.To demonstrate the write distribution better,we present only the largest wear degree of every 5000 pages in this experiment.

First of all,we analyze the write distribution of fio using 2 MB I/O request size.Based on the experimental results illustrated in Fig.6,we can observe that NOVA,DWARM,WMAlloc,and WMAlloc-BMT achieve similar wear-leveling.This is because the fio tests write sequentially to an existing 200 GB file and the pmem0 is 256 GB;then,the size of the data written to PM is small.Therefore,these wearleveling-aware allocators,i.e.,DWARM,WMAlloc,and WMAlloc-BMT,can benefit less from this test.

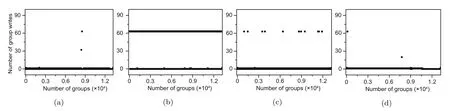
Fig.6 The write distribution in fio: (a) NOVA;(b) DWARM;(c) WMAlloc;(d) WMAlloc-BMT

Second,we analyze the write distribution in createdelete-swing tests.In this experiment,the maximum count file is 400 000.The experimental results are shown in Fig.7.We can observe that the maximum numbers of writes of NOVA and DWARM are larger than those of WMAlloc and WMAlloc-BMT.Specifically,the maximum numbers of writes of NOVA,DWARM,WMAlloc,and WMAlloc-BMT are 166,187,147,and 96,respectively.Compared with NOVA and DWARM,we can conclude that WMAlloc can reduce the maximum number of writes by 12.93% and 27.21%,respectively.Meanwhile,WMAlloc-BMT can reduce the maximum number of writes by 53.13%compared with WMAlloc.

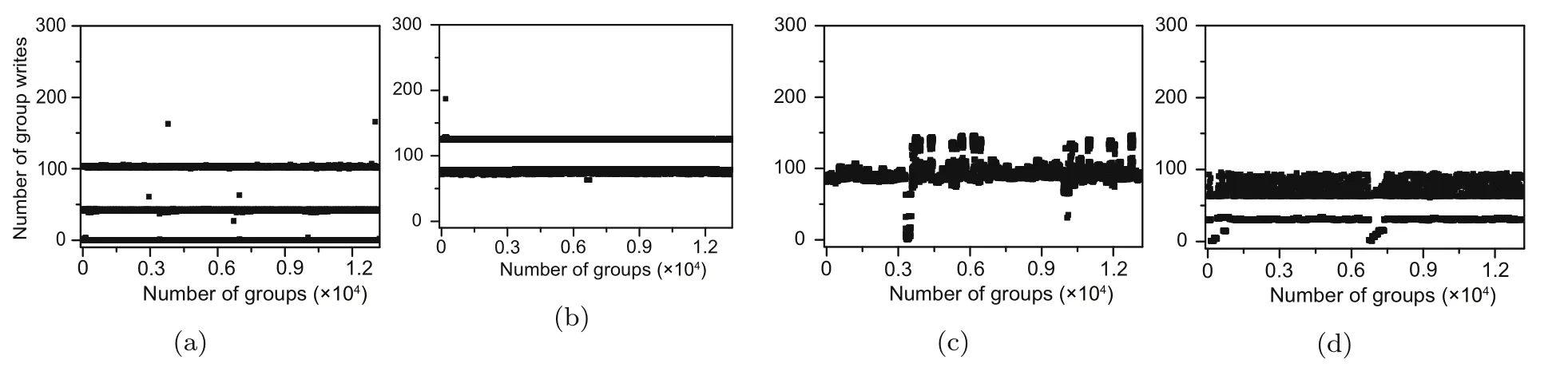
Fig.7 The write distribution in createdelete-swing: (a) NOVA;(b) DWARM;(c) WMAlloc;(d) WMAlloc-BMT

Third,we analyze the write distribution by fileserver.In this experiment,the maximum count file is 400 000.As shown in Fig.8,we observe that NOVA leads to severely unbalanced write to PM,which means that NOVA can cause heavy wear on the PM.Specifically,the maximum numbers of writes of NOVA,DWARM,WMAlloc,and WMAlloc-BMT are 813,171,103,and 93,respectively.Compared with NOVA and DWARM,we can conclude that WMAlloc can achieve 689.32% and 66.02% maximum write number reduction,respectively.Meanwhile,WMAlloc-BMT can achieve 10.75%maximum write number reduction compared with WMAlloc.

Fig.8 The write distribution in fileserver: (a) NOVA;(b) DWARM;(c) WMAlloc;(d) WMAlloc-BMT

Finally,we analyze the write distribution of the postmark workload.In this experiment,the maximum count file is 40 000.The experimental results are shown in Fig.9.Akin to fileserver tests,NOVA can also cause seriously unbalanced wear on PM.Specifically,the maximum numbers of writes of NOVA,DWARM,WMAlloc,and WMAlloc-BMT are 909,469,142,and 134,respectively.Compared with NOVA and DWARM,we can conclude that WMAlloc can achieve 540.14% and 230.28% maximum write number reduction,respectively.Meanwhile,WMAlloc-BMT can achieve 5.97%maximum write number reduction compared with WMAlloc.

Fig.9 The write distribution in postmark: (a) NOVA;(b) DWARM;(c) WMAlloc;(d) WMAlloc-BMT

The reasons why WMAlloc can achieve superior wear-leveling than NOVA and DWARM are as follows.First,the design of NOVA ignores wearleveling of PM,which can lead to severely unbalanced writes among the PM pages.Second,DWARM supports only single-grained allocation,of which the log area suffers from heavier wear.In addition,the set subrange is closely related to the write distribution,and it is hard to gain a tradeoffbetween accuracy and performance.Specifically,a large subrange can lead to seriously unbalanced writes.On the contrary,a small subrange can cause severe performance degradation.Finally,WMAlloc provides multi-grained allocation,which uses minheaps to organize all unused blocks and allocate the least-worn block from the corresponding min-heap for each allocation request.WMAlloc-BMT refines the granularity of min-heaps to avoid the splitting of large blocks during block migration compared with WMAlloc;thus,WMAlloc-BMT can significantly relieve the fragmentation problem to maintain a greater number of large blocks than WMAllc.Therefore,WMAlloc-BMT can reduce the allocation times of large blocks compared with WMAlloc.

5.3 Overall performance

In this subsection,we first evaluate the performance of NOVA,DWARM,WMAlloc,and WMAlloc-BMT with fio workloads.The throughput (in MB/s) of writes with different I/O request sizes in fio are shown in Fig.10a.The experimental results show that the throughput of WMAlloc outperforms that of DWARM with 2.14× on average and achieves a throughput similar to that of NOVA in all cases (degrading the throughput by 2.0%to provide a more balanced write distribution).Compared with DWARM,WMAlloc achieves higher wear-leveling with less overhead.When the I/O request size is 1,2,and 4 KB,the performance of DWARM is similar to those of NOVA,WMAlloc,and WMAlloc-BMT.However,when the allocation granularity is≥4 KB,its performance disadvantage rapidly scales to about 3.11×at 128 KB.This is because DWARM supports only single-granularity allocation.When the allocation granularity is≥4 KB,DWARM must conduct more rounds of allocations to satisfy a request.Moreover,WMAlloc-BMT further expands the advantages and outperforms DWARM with 2.17×on average.This advantage is attributed to the conditional wear inheritance mechanism of BMT,as it eliminates most recalculations of wear degree of remaining blocks after small-grained allocations.

Fig.10 The overall performance: (a) fio;(b) createdelete-swing;(c) fileserver;(d) postmark

Second,we use the createdelete-swing workload to conduct the evaluation.As shown in Fig.10b,WMAlloc outperforms DWARM with 2.09×.This is because the createdelete-swing workload consistently allocates and invalidates used blocks,which enlarges the drawbacks of DWARM.In other words,the single-grained strategy is intrinsically incompatible with various I/O patterns.Compared with NOVA,WMAlloc achieves only-4.68%performance degradation.Though,our BMT mechanism further improves the performance by 9.76% compared with WMAlloc and is even 4.60% better than NOVA.The reason is that BMT refines the allocation granularity,which significantly reduces the splitting of large blocks.As a consequence,the fragmentation problem caused by the recycled blocks has been alleviated.

Besides,we adopt another filebench workload,fileserver,to evaluate the throughput of the four solutions.Fig.10c shows the throughput of the three mechanisms in various numbers of files.In this evaluation,WMAlloc outperforms DWARM by 1.42%.Benefiting from the optimized search process of min-heaps,WMAlloc-BMT achieves performance improvement of 4.39%and 2.04%against WMAlloc and NOVA,respectively.

Finally,we evaluate the performances of four schemes with the postmark workload.We set the total number of files as 10 000,20 000,and 40 000,separately.The total elapsed time of the four solutions is shown in Fig.10d.Performing the same number of transactions,DWARM consumes the most time.The elapsed time of WAMlloc is 32.26% less than that of DWARM and 15.42% less than that of NOVA.WMAlloc-BMT further reduces the elapsed time by 17.83%on average compared with WMAlloc.

In summary,the performance of DWARM is much poorer than that of NOVA,while WMAlloc and BMT are much more competitive.This is because DWARM supports only single-grained allocation,which produces more log entries than NOVA and our solutions.Moreover,to guarantee the strongest data consistency,the newly created entries need to be persistent to PM immediately using the flush instructions (e.g.,mfence and clflush).More log entries of DWARM need to be flushed back to PM more times,which can severely degrade the performance.On the contrary,WMAlloc supports multi-grained allocation.Compared with NOVA,the time complexity of our allocation is almostO(1),while that of NOVA is not necessarilyO(1),especially when there are massive fragments in the front of its RB tree.Although WMAlloc spends some time managing the wear-leveling mechanism,it saves considerable time in allocating and releasing blocks.Moreover,the BMT mechanism further mitigates the redundant overhead of indexing and splits.The above experimental results highlight the advantages of WAMlloc and BMT mechanisms.

6 Conclusions

In this paper,we have studied multi-grained allocation and wear-leveling methodology in PM.We propose a Wear-leveling-aware Multi-grained Allocator (WMAlloc),which achieves wear-leveling of PM while improving the performance of PM file systems.We further propose a bitmap-based multiheap tree (BMT) to enhance the performance and wear-leveling of WMAlloc.Experimental results show that WMAlloc can achieve 4.11× and 1.81×lifetime with four workloads on average,compared with NOVA and DWARM,respectively.Furthermore,WMAlloc-BMT can achieve 1.17× lifetime and 1.08× performance with four workloads on average,compared with WMAlloc.

Contributors

Zhiwang YU,Runyu ZHANG,Chaoshu YANG,and Shun NIE designed the research.Zhiwang YU and Shun NIE implemented the prototypes.Zhiwang YU,Runyu ZHANG,Chaoshu YANG,and Shun NIE conducted the evaluations.Zhiwang YU and Shun NIE drafted the paper.Duo LIU helped organize the paper.Runyu ZHANG and Chaoshu YANG revised and finalized the paper.

Compliance with ethics guidelines

Zhiwang YU,Runyu ZHANG,Chaoshu YANG,Shun NIE,and Duo LIU declare that they have no conflict of interest.

Data availability

The data that support the findings of this study are available from the corresponding authors upon reasonable request.