基于动态重叠网格的阀芯振荡空化的研究

刘乐璠, 郑 直, 闵 为, 冀 宏

(兰州理工大学能源与动力工程学院, 甘肃兰州 730050)

引言

在液压系统中,锥阀是一种常用的阀结构之一,其通常由阀芯、阀座和弹簧组成,主要作为压力调节阀来调节或限制系统压力。但压力调节阀经常会出现失稳振动,引起系统压力剧烈波动,对整个液压系统的稳定性和可靠性造成了巨大的影响。

为了改善液压系统中锥阀普遍存在的振荡情况,本研究以先导级压力调节锥阀为研究对象,研究其阀芯振动过程中的空化问题,对于锥阀结构设计优化以及整个液压系统而言,具有重大意义[1]。

人们很早就意识到锥阀的轴向振动易导致系统压力的大幅波动,并在这方面开展了大量研究。YONEZAWA等[2]研究了压力控制阀阀芯的振动频率及幅值,结果表明:阀芯的小幅振动是由系统压力波动引起的,而大幅振荡则为弹簧-质量振动系统的自激振荡;HAYASHI[3]的研究表明,阀芯与阀座的碰撞、液动力的滞后均会导致锥阀阀芯出现大幅振动。谢海波等[4]研究了不同阀口形态对锥阀液动力的影响,认为随着阀口形态的变化,阀芯所受液动力的大小和方向都会随之变化。

上述研究指出了诸多影响阀芯轴向振动的因素,随着计算流体力学和流场可视化技术的发展, 锥阀的轴向振动和空化问题又重新引起了学者们的关注。KUMAGAI等[5]利用高速摄像机构建了锥阀的阀芯振动和流场可视化试验系统,通过图像处理的方法研究了阀芯轴向振动位移、气泡数量和阀口压力之间的关系,并提出了空化条件下阀芯的失稳振荡过程假设;闵为等[6]通过COMSOL流固耦合的方法研究了锥阀的轴向振动现象,结果表明阀芯轴向振动过程中阀口逆压力梯度区的压力波动幅值和相位会产生剧烈变化,对阀芯轴向振动幅值产生较大影响;刘子晨[7]使用传统的动网格技术对阀芯振荡流场进行了仿真,发现想要实现大幅度变形的狭窄流道计算,无论使用非结构网格或结构网格运动方式,网格质量都会严重下降,极易出现负体积现象无法完成计算。袁聪等[8]针对锥阀空化射流进行了数值模拟,将结果与试验进行对比,解释了在试验中观测到的空化形态。

对于重叠网格的研究,1983年由NASA Ames研究中心的STEGER J L等[9]首次发表相关文章。人们将重叠网格技术大量应用于航空航天和船舶领域[10],这种类型的仿真往往拥有巨大的背景网格区域,和锥阀流场需要的小间隙流场有一定的区别。HADZIC H[11]开发了一种可用于非结构化网格的,基于有限体积法的重叠网格技术(网格内插值),这也是STAR-CCM+中重叠网格技术的基础。近年来STAR-CCM+在其软件中加入了重叠网格零间隙(ZeroGap)及棱柱层压缩(Prism Layer Shrinkage,PLS)功能,人们才逐渐开始将重叠网格用于小间隙复杂流道中。LV Xinbei等[12]运用重叠网格模拟喷嘴挡板阀中的流场和空化情况,认为空化周期性和挡板的运动周期性有极强的相关性。LAI Zhounian等[13]运用重叠网格技术模拟了双碟式止回阀在管路中的压力状况,获得了阀片的运动特性。

在锥阀流场研究领域,对于重叠网格的运用极少。相较于传统动网格,重叠网格能在保证网格质量和运算速度及精度的同时,实现更大的运动范围[14]。故本研究在闵为等[1]试验研究的基础上,将可视化试验与动态重叠网格技术相结合,对锥阀阀芯的轴向振荡启闭过程中的空化现象展开研究。

1 试验装置与条件

1.1 试验装置与步骤

试验装置如图1所示, 电机M1驱动定量泵1, 提供15 L/min的恒定流量。

试验模型中,阀体20由有机玻璃制成,可使高速摄像机24清晰方便地拍摄到阀芯17的运动情况和试验模型阀内流场,阀芯17通过连杆与LVDT位移传感器21的铁芯相连,以便于测量阀芯的轴向运动位移,位移传感器的测量范围是-5～5 mm,测量精度为满量程的0.5%,锥阀进出口压力分别由15、22两个压力传感器测量,流经模型的流量由流量计23测得,其测量范围为0.5～5 L/min,测量精度为满量程的0.5%,高速摄像机24的拍摄速率为10000 帧/s,数据采集仪26的采样周期为0.1 ms。

试验时,先将回油节流阀10调至最大开口,然后慢慢调节进油节流阀9,同时观察流量计23,观察到流量计23数值到3.5 L/min时,即流经试验模型的流量为3.5 L/min,停止调整进油节流阀9,准备开始正式试验数据记录。

启动高速摄像机24和数据采集仪26,然后让换向阀8由中位换成右位,即可完整地记录锥阀的整个运动过程。

1.2 试验条件

试验模型是作为导阀使用的锥阀,由于仅研究阀芯的轴向振荡过程与空化现象,故没有考虑阀芯前端的固定阻尼孔。具体试验参数如表1所示。

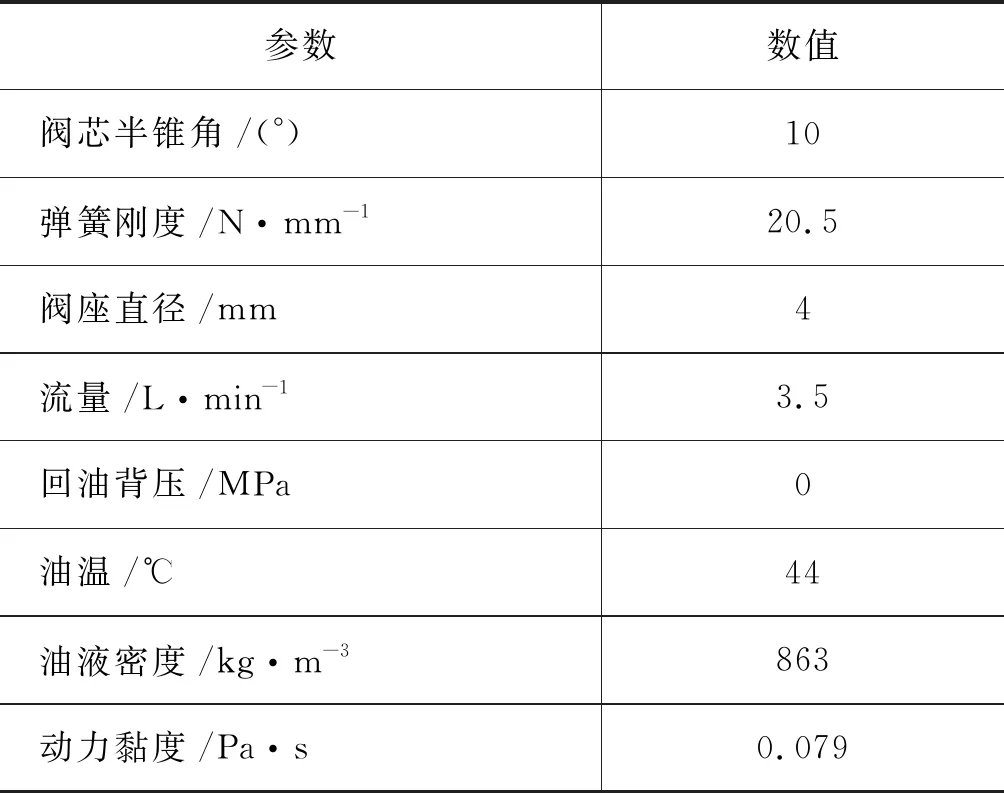
表1 试验参数

1.3 试验结果

如图2所示,从持续7 s的试验数据中截取了其中一段展示,锥阀开启后达到平衡状态时,阀芯在0.4 mm 的阀口开度附近失稳振荡,进口压力在1.7 MPa 左右以0.7 MPa的幅值波动,其波动幅值达到调定压力的41%。

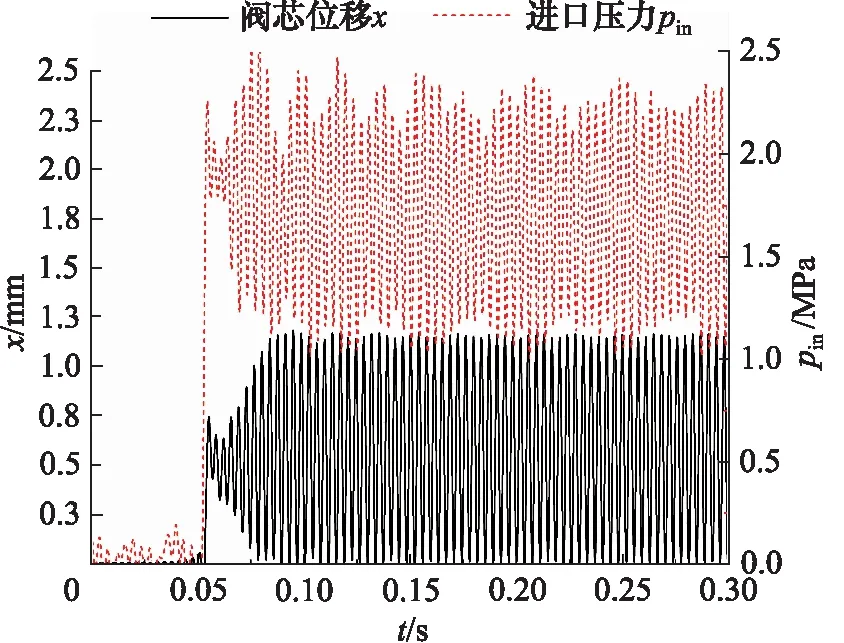
图2 进口压力与阀芯位移

选择阀芯处于稳定振荡后的3个振荡周期进行模拟,并将试验中测量的阀芯位移数据,以表格(.csv)的形式导入STAR-CCM+的表格(Tables)中。

同时,为了探究在相同条件下,不同阀芯运动速度对流动的影响,对试验数据分别进行了时间缩短一倍和放大一倍的处理,分为慢速、中速(试验)和快速三种情况,如图3所示,并以此数据进行仿真。

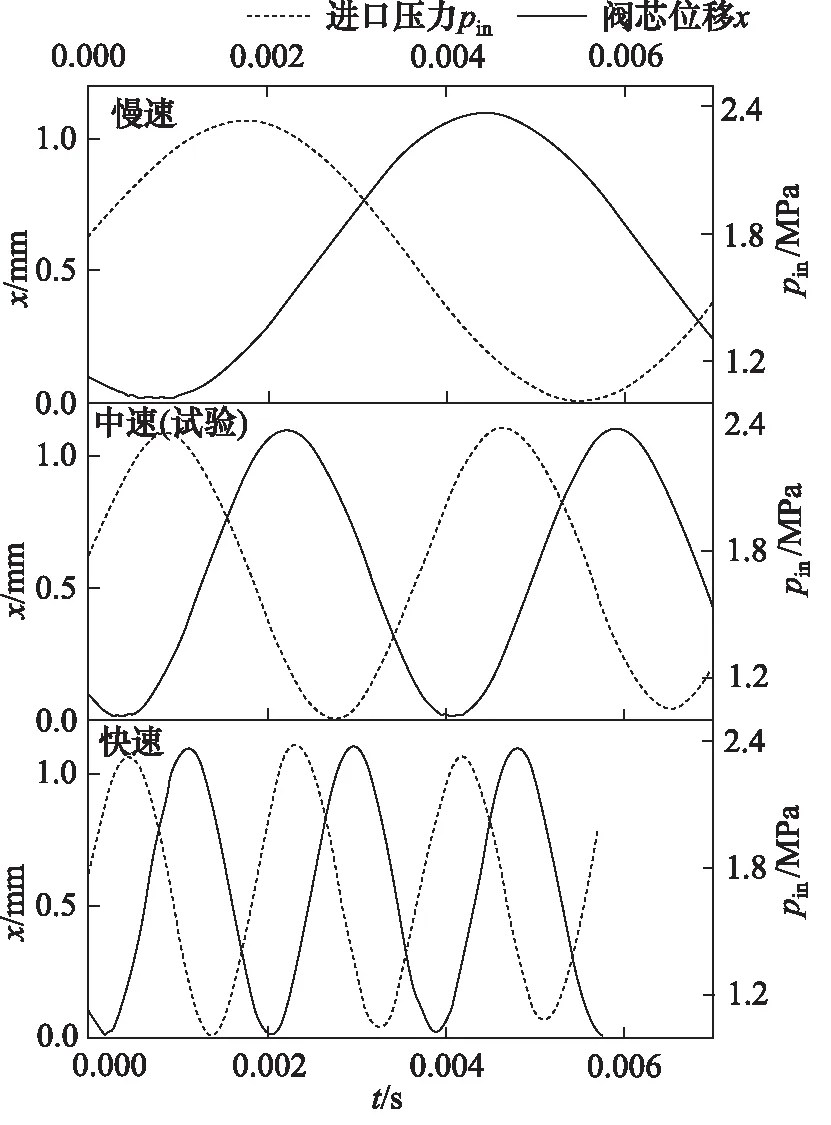
图3 慢中快三种不同的仿真条件

试验产生的空化现象将与数值模拟相结合在下一节分析。

2 数值模拟

2.1 锥阀几何模型及重叠网格中的识别技术

如图4所示,本研究对照试验中的可视化模型建立了计算几何模型,为了节省计算资源,提高计算效率,且由于锥阀流道本身具有圆柱体对称性,3D几何被转换为2D网格,采用二维绕轴回转体网格计算。

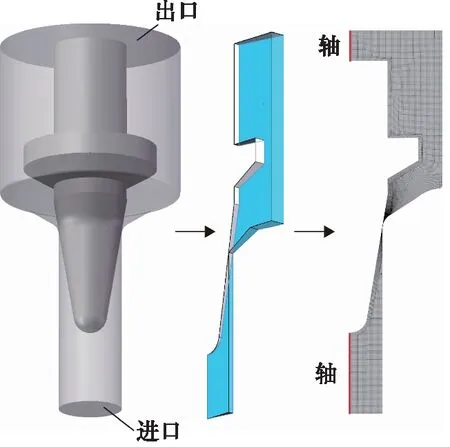
图4 计算区域示意图

本研究中使用的重叠网格技术,一般分为两个区域: 背景网格区域和贴体网格区域。在OpenFOAM的传统重叠网格中,重叠网格类型有四种,重叠网格类型编号和颜色参照图5:

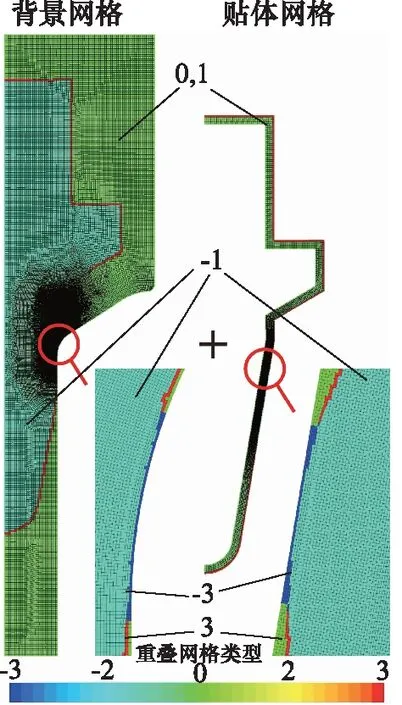
图5 重叠网格组成示意图

(1) -1—不活动网格(洞网格),在不活动网格中,不对任何方程进行求解。但是,如果贴体网格区域已移动,这些网格可能会变为活动状态。

(2) 0—活动网格,在活动网格中,将对离散控制方程进行求解。

(3) 1—供体网格,最接近另一个区域中的受体网格的活动网格,故和活动网格同色。

(4) 3—受体网格,位于重叠网格交界面处。变量值从一个区域的供体网格插值到另一个区域中的受体网格。一个区域中的供体网格是最接近另一个区域中的受体网格的活动网格。

而在STAR-CCM+中,重叠网格类型即为图5所示,相较于传统重叠网格类型,STAR-CCM+还有一种新类型:

(5) -3—零间隙(ZeroGap)区域内的不活动网格,此种网格和不活动网格相同,不参与计算,但STAR-CCM+会对此种网格施加固壁边界条件(目前在OpenFOAM中无法实现),能将流动封闭,实现阀口关闭的效果,这就是STAR-CCM+中零间隙(ZeroGap)技术的关键之处,

此外,STAR-CCM+中的棱柱层压缩(Prism Layer Shrinkage)技术,可将缝隙中的网格进行变形压缩处理,如图5中“-3”网格所示,使其依旧能达到计算要求,节省网格数量。

将背景网格和贴体网格组合成为一套网格,如图5经过挖洞后成为图4最右侧网格开始计算。

2.2 基本方程

阀内流场数值计算的连续性方程、动量方程、输运方程如下所示:

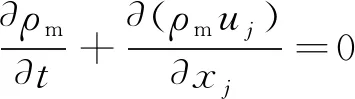
(2)

ρm=ρl(1-αv)+ρvαv

(4)

μm=μl(1-αv)+μvαv

(5)

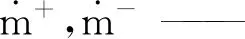
ρm—— 混合密度

μm—— 混合黏度

ρv—— 气相密度

αv—— 气相体积分数

2.3 空化模型

本研究中采用的Schnerr-Sauer空化模型基于Rayleigh-Plesset(RP)方程。

Schnerr-Sauer空化模型凝结源相和蒸发源相表达式为:

(6)

式中, RB—— 初始气泡半径,其值为1×10-6m。

2.4 数值模拟设定

根据试验所提供的数据,采用压力入口及压力出口边界条件,壁面为无滑移壁面,流体介质两相均视为不可压缩的常温流体,物性参数如密度黏度均为定值。进口压力在1.7MPa左右以0.7MPa的幅值波动,阀芯位移同样也取自于试验数据,在0.58mm左右以0.6mm的幅值振荡。详细参数设定见表2,其中饱和蒸气压为绝对压力,而进出口所设压力为表压。且使用自适应时间步将最大CFL数设为1,以保证瞬态模拟结果的可靠性。

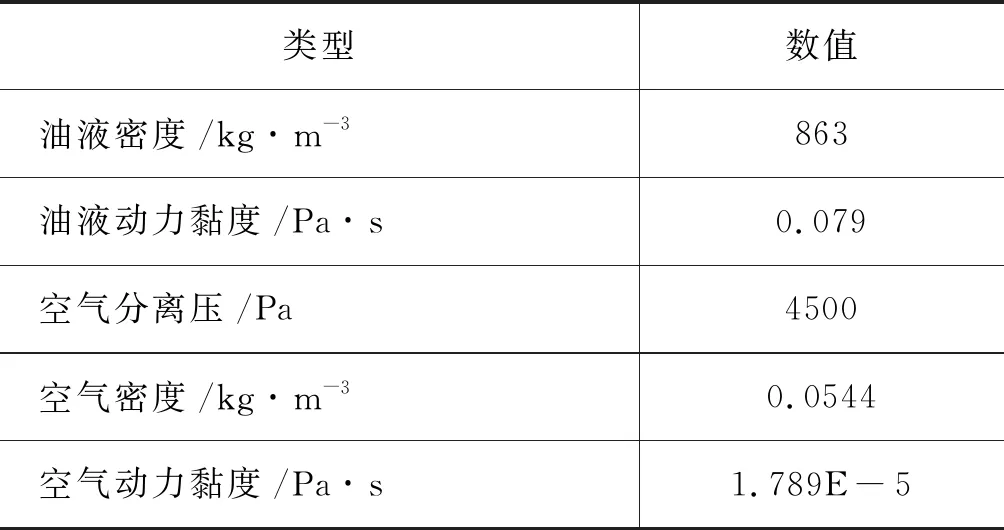
表2 仿真参数设定

本研究中的流动介质为液压油,液压油中的空化形成的物理机理是溶解在油中的空气, 因为压力降低从油中析出的过程,此种类型的空化被称为空气型空化[15]。

3 结果分析

3.1 阀口开启阶段-射流空化

当锥阀达到稳定振荡状态,阀芯向上运动,导致阀口开启时,阀口处产生射流,在阀口处形成低压区产生云状空化,并随之脱落,如图6圆圈处,试验与仿真图像吻合较好。

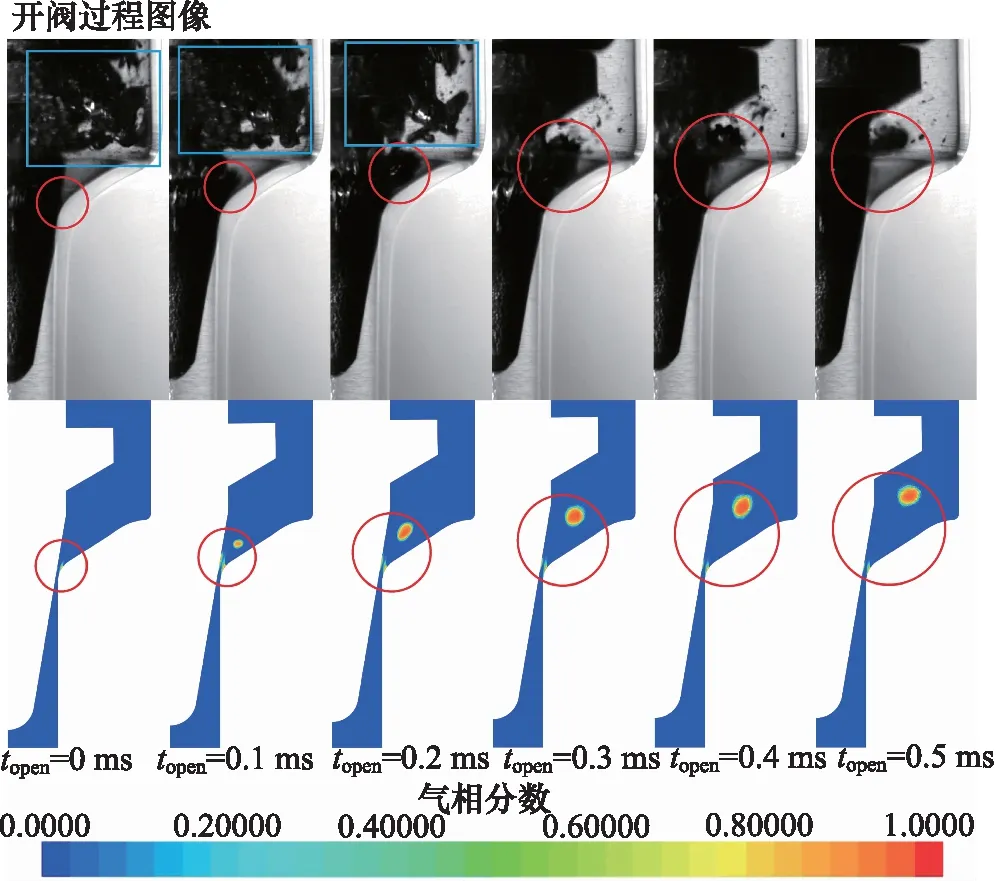
图6 开阀过程试验拍摄图像与STAR-CCM+仿真图像对比

图6显示了6张连续帧试验图像,即0.6 ms时间段内的瞬态空化的试验图像。阀芯开启时,从阀口前部喷出的高速射流在阀座转角处形成低压区,产生云状空化,迅速脱落并向阀口后方移动。0.6 ms后,脱落的云状空化,移动到压力高于空气分离压的区域,随即消散。

此处需要特别说明的是,阀芯振荡空化中存在两种空化类型,图6中的方框(前三张图像)中的空化属于压力波空化,为阀口关闭阶段产生的空化(将在3.2节讨论),还未完全消散;而图6圆圈处的空化为射流空化。

3.2 阀口关闭阶段-低压压力波空化

当锥阀达到稳定振荡状态,阀芯向下运动,导致阀口关闭时,造成瞬间断流;阀口前部由于油液无法通过阀口,压力增大(这会使得阀口打开时产生射流);阀腔后方液体由于惯性继续向外运动,造成阀腔内部压力骤降,从阀口处形成一股低压压力波传递到后方,液体中的空化核和微小气泡受低压压力波影响迅速变大形成空泡,如图7所示。

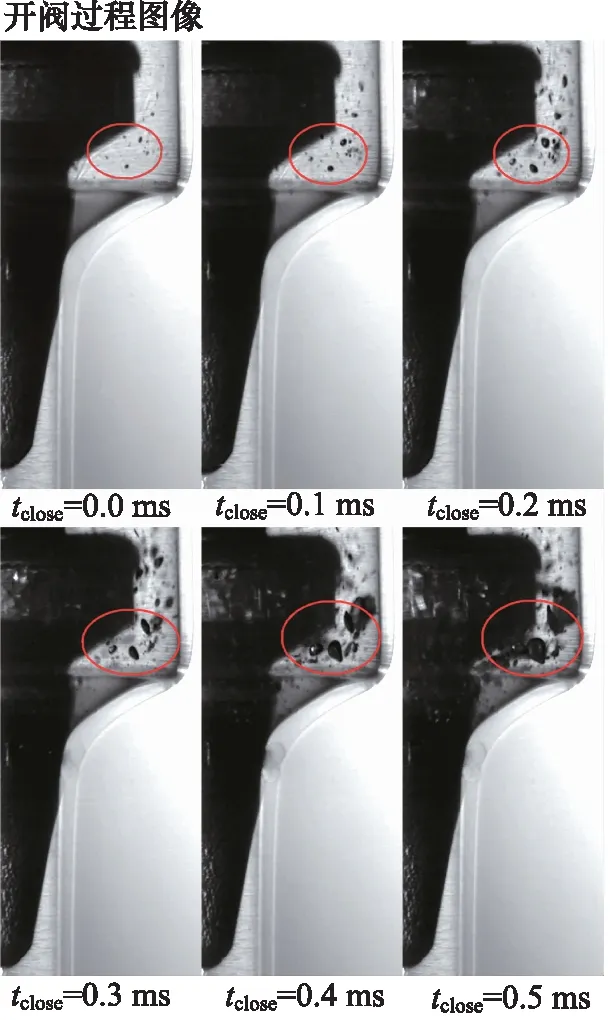
图7 关阀时阀口后方空泡逐渐增大0.5 ms内的图像

此时形成的空泡并未像阀口开启时,因高速射流在阀口转角处形成的低压区域而产生,而是随机产生于阀口后方受到低压压力波影响的区域内。如图7所示,阀口关闭瞬间,由高速摄像机拍摄的阀口后方空泡逐渐增大过程。试验图像中的气泡基本没有改变位置,而是在原地受到低压压力波的影响,迅速增大,然后连成一片,形成了在上一小节,图6左上方框中看到的,由于阀口关闭而产生的空泡还未消散的现象。

在数值模拟中,如图8所示,阀口关闭到0.1 mm时,阀口处流速大幅度降低,下降至4 m/s,虽然在阀腔后部有涡旋出现,但整体流动处于停滞状态,与试验图像相符。但我们并未能捕捉到低压压力波和低压压力波引发的空化,这种情况也许与STAR-CCM+中的空化算法为不可压缩算法有关。

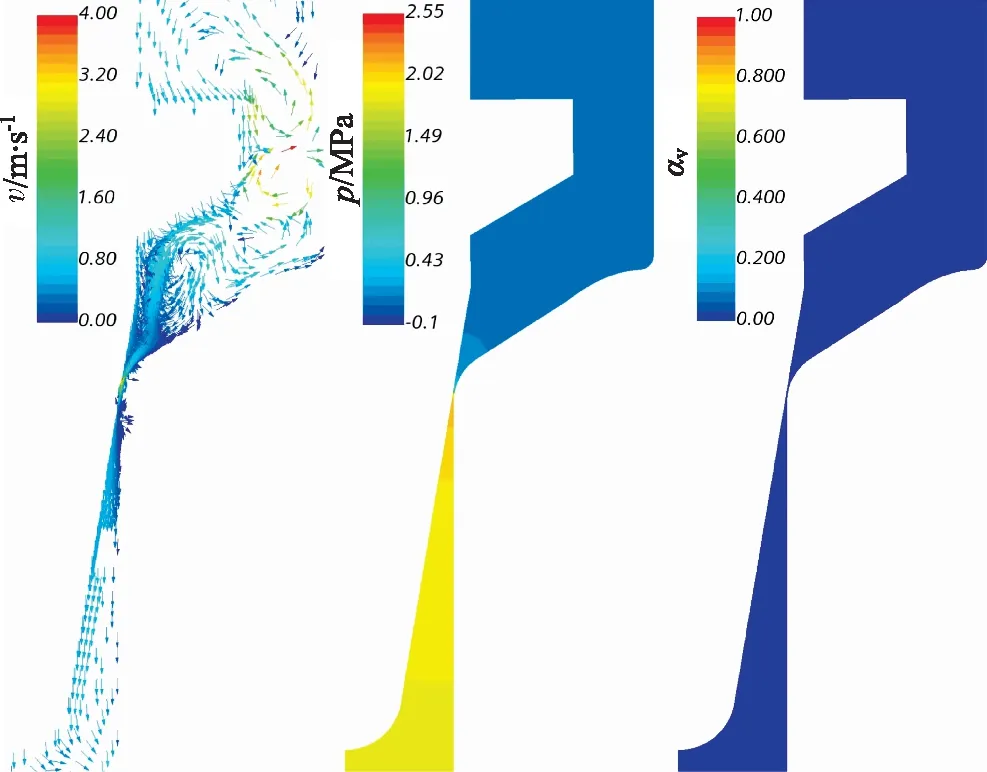
图8 阀口接近关闭时(开度为0.1 mm)的速度压力和气相分数

3.3 阀芯运动速度对流动的影响

在对三种不同阀芯运动速度的情况进行仿真后,取阀口处流速与阀口开度数据,并引入了慢中快三种阀芯运动速度(详见1.3节)作出图9。

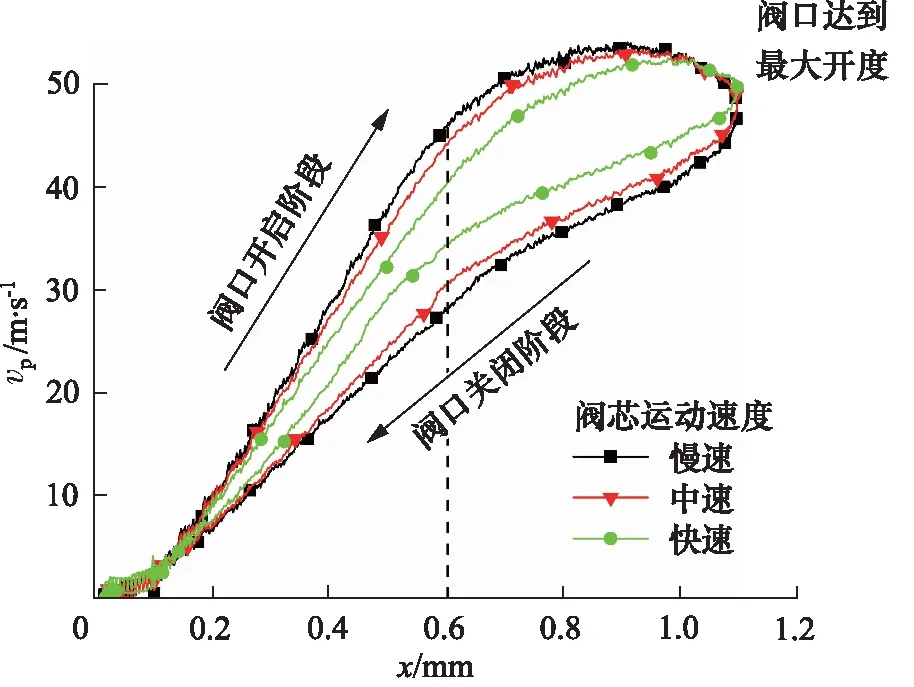
图9 阀芯在不同运动速度下阀口开度与阀口处流速关系

如图9中竖向虚线处所示,可见在阀口开启到相同开度(0.6 mm)时,阀芯运动速度越快,阀口处流速越低;而在阀口关闭到相同开度时,阀芯运动速度越快,阀口处流速越高。

当阀口同时开启到1 mm时,三种不同阀芯运动速度的流场情况如图10所示,可见随着阀芯运动速度的增大,阀口射流生长的程度减小。

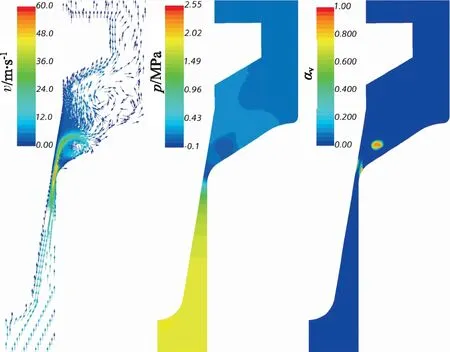
图10 慢速阀芯运动

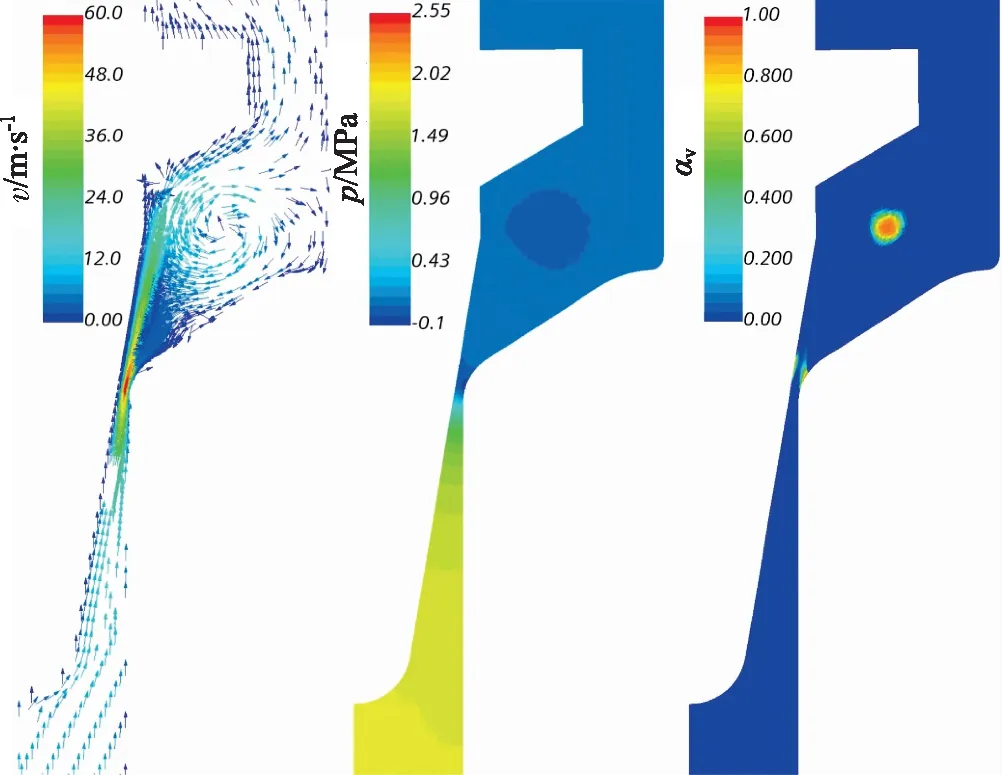
图12 快速阀芯运动

在慢速阀芯运动的仿真结果中,射流已处于中后期,射流形成的漩涡其携带的脱落型空化位置也远离阀口处。

射流形态位于慢速运动和快速运动二者之间,脱落型空化的位置也同理。

在快速阀芯运动的仿真结果中,射流形成漩涡不久,随之运动的脱落型空化的位置也靠近阀口处。

在中速(试验数据)阀芯运动的仿真结果中,阀口处的流速数据以及阀芯的运动情况做出图13。

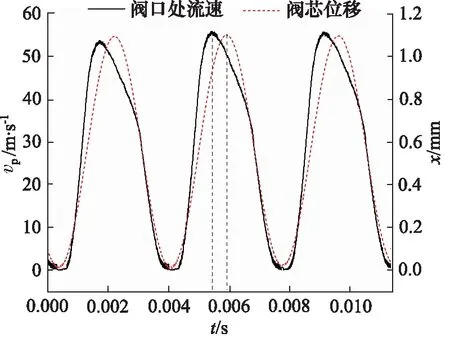
图13 阀口处流速与阀芯位移

观察对比曲线可知,锥阀阀芯在达到稳定振荡状态后,阀口在开启过程中时,阀口处的流速也随之增大,油液从阀口处喷出,在阀口处形成射流,如图11所示。

阀芯开启但未达到最大开度时,如图13中第一条竖向虚线所示,此时阀口处流速是最快的,同时因射流产生空化(如图11所示),但在阀芯完全开启后,阀口处流速慢慢减小,如图13第二条竖向虚线所示,此时,由于阀口处流速降低,已不符合产生脱落型空化的条件。

上述三种情况与图9曲线描述的情况相结合,认为阀芯运动速度越快,射流生长越慢,阀口处射流速度越低,阀芯的运动速度会对流动造成显著影响。

经分析认为是由于液体的惯性所致:本研究中仿真的阀流场,大部分液体存在于阀口的前部腔体和阀口的后部腔体中,少量液体存在于阀口处。阀口处的流动速度连接阀流场前后腔的流动速度,当阀芯开启速度增大时,液体由于惯性依旧保持之前的低速流动状态,存在一定的“延迟”情况。阀芯开启速度越快,阀口开度越先达到一定开度(如图9 0.6 mm开度的竖向虚线),所以才会出现图9上阀芯开启速度越快,阀口处流速越低的情况;同理,在阀口关闭到相同开度时,阀芯关闭速度越快,液体由于惯性依旧保持之前的流动状态,阀口处流速越高。

4 结论

本研究采用可视化的试验研究方法以及CFD数值模拟对锥阀轴向振荡启闭时的空化现象进行了研究。

综合试验和仿真的结果,结果表明:

(1) 运用STAR-CCM+重叠网格中的零间隙和棱柱层压缩技术,成功实现锥阀流场的开启和关闭,完成了传统动网格未能完成的任务,并以此网格为基础进行阀芯振荡空化仿真,与试验结果吻合较好;

(2) 开阀时产生空化的原因是由于阀口开启时的射流,该结论从试验和仿真结果上均得到证实;关阀时,从试验结果来看,是由于阀口断流后产生的低压压力波,使气泡在原地膨胀形成空化,而从仿真结果来看,阀口的关闭使流动停止,但由于底层算法原因,未能准确的捕捉到低压压力波;

(3) 不同的阀芯运动速度对阀内流动有影响。当阀芯开启速度增大时,液体由于惯性依旧保持之前的低速流动状态,存在一定的“延迟”情况。阀芯开启速度越快,阀口开度越先达到一定开度,阀口处流速越低;同理,在阀口关闭到相同开度时,阀芯关闭速度越快,液体由于惯性依旧保持之前的流动状态,阀口处流速越高。

上述结论为锥阀的结构优化提供了一定的理论依据。同时本研究也将动态重叠网格技术应用到小间隙复杂流场研究中,对类似的复杂流场的数值模拟有一定的参考价值。