滑阀阀芯凹角结构CFD仿真分析与优化设计

张敬芳, 张宇航, 余 聪, 杨明昆, 张 勇, 艾 超

(1.河北机电职业技术学院, 河北邢台 054000; 2.燕山大学机械工程学院, 河北秦皇岛 066004)

引言

液压滑阀由于容易平衡液压径向力和轴向力,具有操纵力小、动作可靠、工艺性好等特点,在换向阀中应用最为广泛[1]。当油液流经阀口,相当于薄壁孔口出流问题,由于过流面积的变化,阀口处的压力和速度会发生突变,同时伴随有漩涡、气穴、振动等现象。尤其是小开口时,高压液流的冲洗会增加滑阀阀芯和密封件损坏的风险,从而影响液压换向阀的工作性能和使用寿命[2]。

国内外众多研究人员通过数值模拟和实验的方法,深入研究了液压滑阀的内部流动特性,分析了液压滑阀在使用过程中容易出现的问题,并对液压滑阀的结构加以改进以满足各种复杂工况需求。张晋等[3-4]、朱牧之等[5]、YE Y等[6],采用CFD仿真方法和PIV可视化技术对液压滑阀内部的流场进行可视化分析,研究了阀口开度、入口流量、阀芯结构等参数对阀内的压力分布、速度分布和液动力等流动特性的影响规律。白云飞[7]、何鑫龙[8]、吴施熠徽等[9]引入湍流场协同原理对液压阀内部的流场进行数值模拟和流动场协同分析,从局部流动场协同角度揭示流阻的变化机理。曹飞梅等[10]针对滑阀阀芯凹角处漩涡对滑阀内部流场特性的影响,对阀芯凹角结构进行优化,仿真分析表明斜角加圆弧形结构可更有效平缓流场,提高阀内能量利用率,但没有详尽阐述斜角加圆弧结构对降低阀内能量耗散的影响机理。AMIRANTE R等[11]、ZHANG X等[12]、桂肃尧等[13]结合数值仿真方法和智能寻优算法对液压阀的流量压力特性和动态响应特性进行优化设计,得到了液压阀结构的最优设计方案。

以上研究成果为液压滑阀内部流场特性、阀口流阻特性及液压滑阀结构改进提供理论支撑,但是对液压滑阀阀芯凹角结构对阀内流场流动特性及能量耗散机理的研究还较少。以全周开口滑阀阀芯为研究对象,采用仿真软件Fluent对滑阀入口节流流场进行稳态仿真,得到不同阀芯凹角结构对阀内流场分布、漩涡形成过程、能量损失等特性的影响,并通过粒子群算法对阀芯结构参数进行智能优化,最大程度上抑制阀口处漩涡的生成,降低阀口处液流的能量损失。

1 液压滑阀的物理和数学模型

1.1 液压滑阀物理模型

液压滑阀通过改变阀芯与阀体之间的相对位移来改变流体通路开口的大小,从而控制流体的压力、流量及方向。实际工程中的液压滑阀结构复杂,为了便于计算和研究,选取某6通径O形中位机能单进单出液压滑阀为研究对象,图1为液压滑阀结构示意图,滑阀具体结构尺寸见表1。

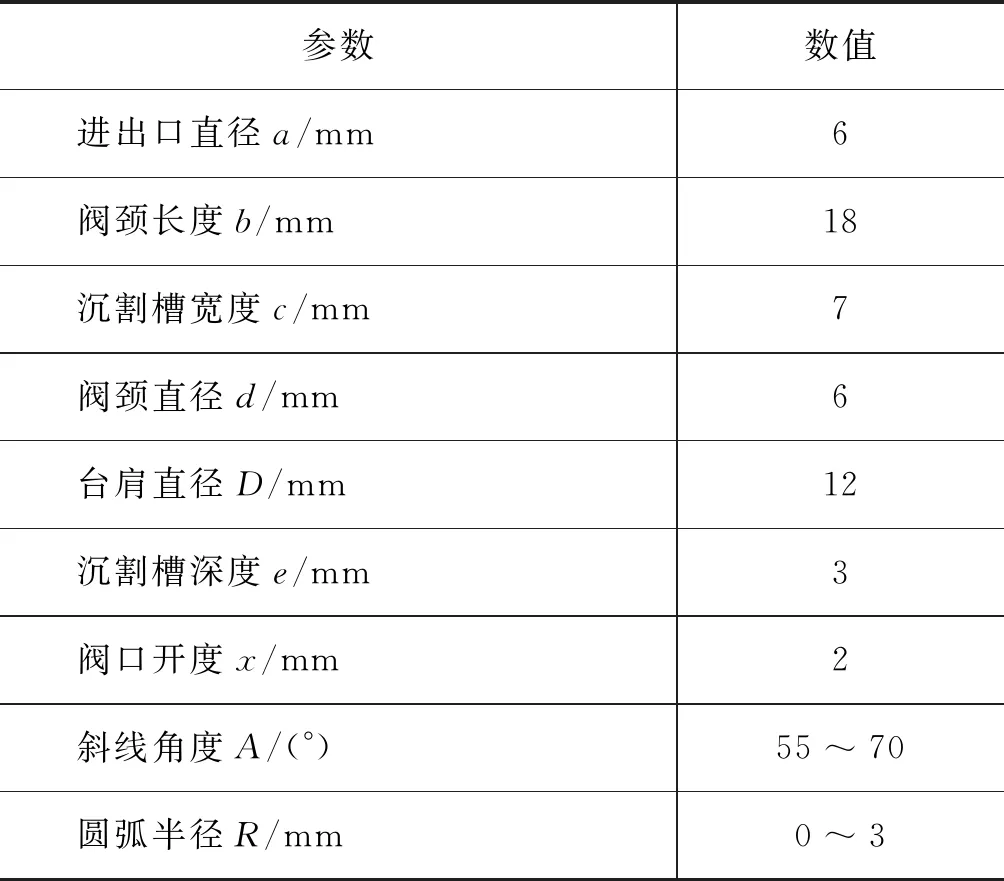
表1 滑阀参数尺寸

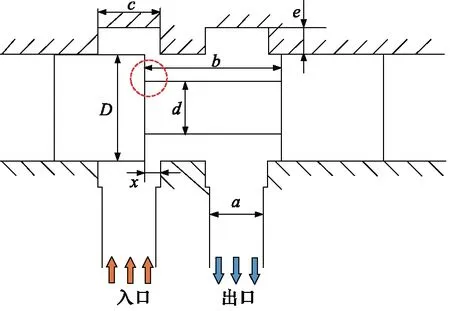
图1 液压滑阀结构示意图

为了比较阀芯凹角形状对阀内流体流动特性的影响,在现有常用阀芯形式的基础上,建立了四种类型的阀芯模型,如图2所示:图2a为直边阀芯,图2b为弧边阀芯,图2c为斜边阀芯,图2d为斜边+弧边阀芯。

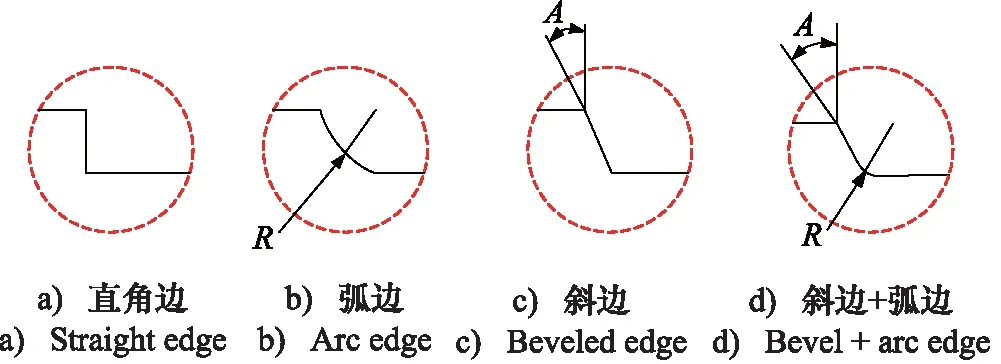
图2 四种类型的阀芯模型

1.2 液压滑阀数学模型

采用有限体积法对液压滑阀内部的流体流动进行数值模拟。为了得到液流在滑阀内部的流动过程,必须求解连续性方程、动量方程和湍流方程。

1) 连续性方程

连续性方程的张量形式可以写为:

式中, ρ —— 流体密度

ui—— 速度张量

xi—— 空间点的坐标,i=1,2,3表示x,y和z方向

2) 动量方程

式中, p —— 静压

τij—— 应力张量

Fi——i方向上的体积力

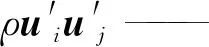
应力张量的表达式为:

3)Realizablek-ε湍流模型

在Realizablek-ε湍流模型中,有关耗散率ε和湍动能k的输送方程表达式如下:

Gk+Gb-ρε-YM+Sk

(4)

式中, Gk—— 平均速度梯度产生的湍流动能

Gb—— 浮力产生的湍流动能

YM—— 可压缩湍流中脉动膨胀对总耗散率的影响

C1,C1ε—— 常量

σk,σε—— Sk,Sε的湍流普朗特数

2 液压滑阀的CFD模型

2.1 网格划分

为了保证网格划分的质量和计算的准确性,采用FluentMeshing对流道模型划分非结构化网格,针对阀口处流体流动状态复杂,设置BOI(BodyofInfluence)对阀口区域的网格进行局部加密,体网格划分方法选择Poly-hexcore,对流体域划分棱柱—多面体—六面体混合网格,滑阀阀口处的网格如图3所示。

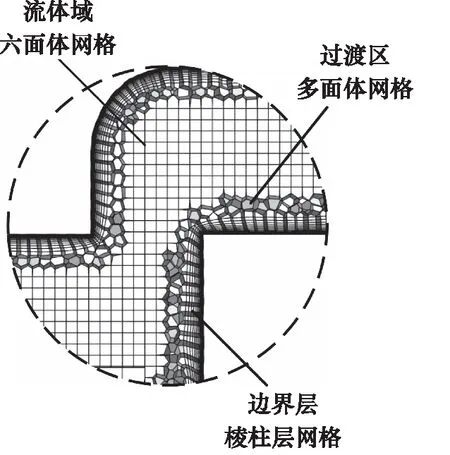
图3 滑阀阀口处网格

2.2 参数设置

针对滑阀内部油液流动复杂的特点,利用Fluent软件进行仿真计算。采用基于压力的求解器,并选择Realizablek-ε湍流模型对滑阀流场模型进行稳态仿真,采取下列仿真模型参数设定:

1) 计算条件

液体介质假设为理想牛顿流体,不可压缩;忽略流体重力、温度对仿真结果的影响,即只开启黏性方程;流体流动状态为单相流,油液密度为870 kg/m3,动力黏度为0.04 Pa·s。

2) 仿真条件

进口设定为速度进口(Velocity-inlet),根据进口体积流量和截面积换算得到入口速度;出口设定为压力出口(Pressure-outlet);壁面设定为无滑移绝热边界条件,具体仿真参数设定如表2所示。

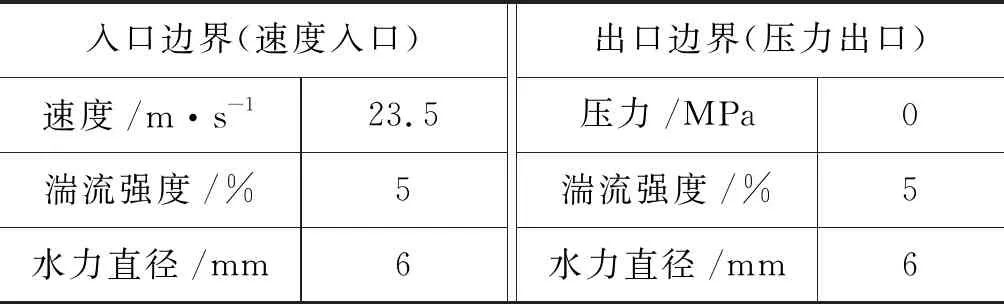
表2 仿真参数

3) 求解器设置

为保证仿真计算的稳健性,求解方法选择压力速度耦合(Coupled)求解方法,梯度插值方法选择基于单元体的最小二乘法插值,为了提高计算精度,其余选型设置为二阶迎风格式。

4) 收敛条件

计算收敛条件设定为:各残差值均低于10-5;监测值波动低于1%,监测量为进口压力和出口体积流量。

2.3 网格独立性验证

调整相应的面网格和体网格尺寸进行网格独立性验证,选取进出口压差作为评估指标,表3为网格无关性分析表,当网格划分数量为49.7万时,继续增加网格数量,计算结果不再有明显变化,认为网格满足独立性要求,最终确定网格数量为49.7万,以保证网格的质量和计算资源的优化配置。此时面网格最大Skewness值为0.40,体网格最小Orthogonal Quality值为0.33,网格质量良好。

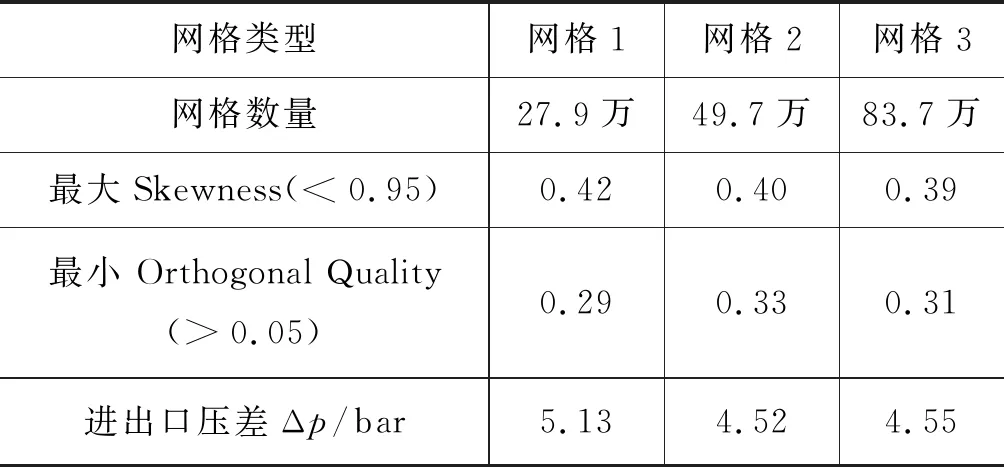
表3 网格独立性分析表

3 液压滑阀流场仿真结果及分析

通过有限元分析软件Fluent对不同阀芯结构的滑阀流场进行仿真,设定滑阀阀口开度x=2 mm,进口流量Q=40 L/min,得到阀内流场的速度及湍流动能分布规律。创建阀内流场X=-2.5 mm的中心截面(以下简称对称面),对称面上的湍流动能分布如图4所示。

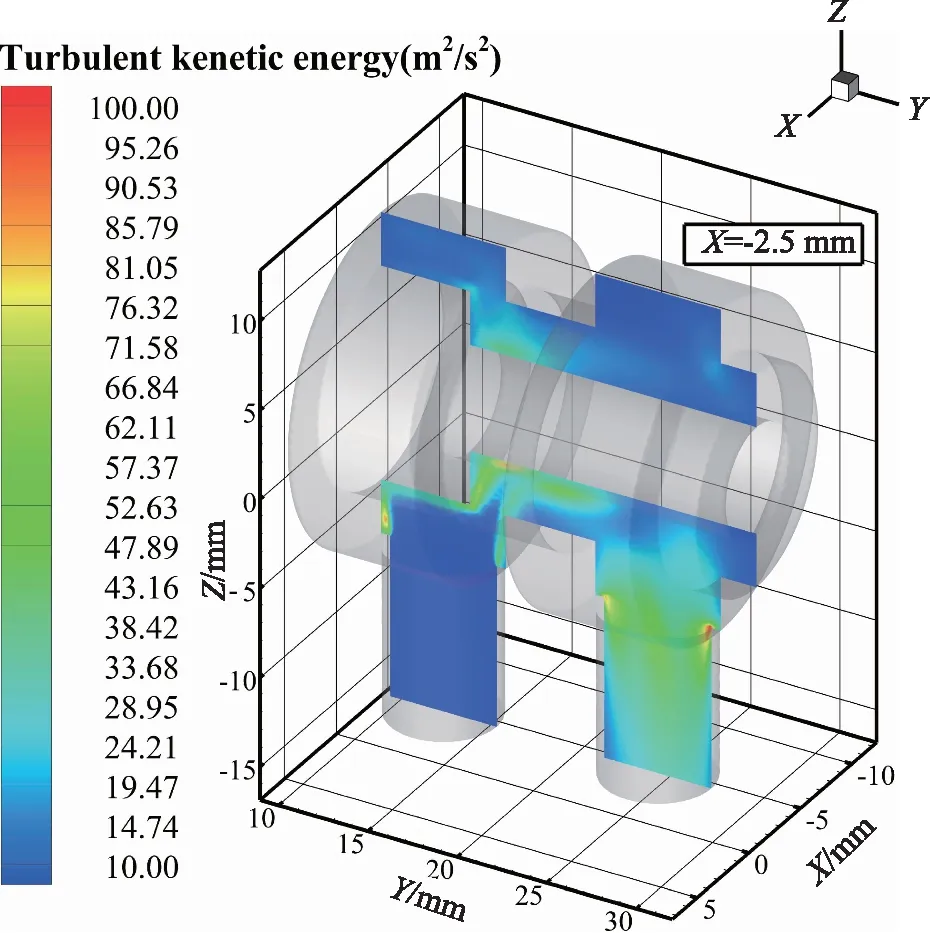
图4 阀内流场对称面上湍流动能云图

3.1 运动状态分析

滑阀流道对称面速度分布如图5所示。由图5可以发现高压流体从进口流入,经过阀口时,流动方向由纵向变为横向,由于滑阀结构的限制和油液黏性力的影响,在阀芯凹角处形成漩涡。由于压降的作用,高速附壁射流流出阀口,冲击阀颈,在阀颈底部形成剧烈漩涡,流体流向出口侧,只有靠近出口管道的流体会直接流出,其他流体都会聚集在阀体的上部,产生大面积漩涡。

图5 滑阀对称面速度分布云图

对比不同阀芯形状的滑阀对称面的流线分布,阀芯凹角结构对阀颈底部及阀体上部漩涡的涡核位置、漩涡面积没有显著影响,但是将凹角形状设计为斜线形可以引导阀口处流线的流入方向,在一定程度上平缓了阀口处的流场,有效抑制阀芯凹角处漩涡的生成。

为了更加准确地分析四种阀芯形状对油液流速的影响,沿着油液流动路线设置了一条监测线,监测y方向上的速度变化情况,图6为四种阀芯形状的滑阀监测线上的速度分布。可以发现四种阀芯结构的滑阀内部的速度变化趋势一致,阀芯结构对阀内速度分布没有显著性差异。油液靠近节流口时,速度逐渐增大,由于压差的影响,在节流口处的速度达到峰值;随着油液不断冲击阀颈,在阀颈底部速度达到第二个峰值。

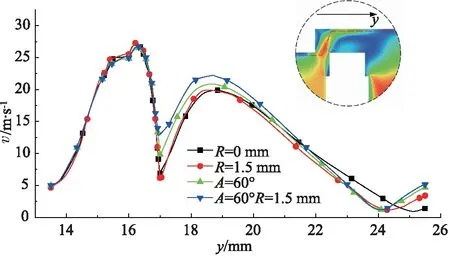
图6 四种阀芯形状的滑阀监测线上的速度

3.2 湍流强度分析

滑阀对称面湍流动能分布如图7所示,从图5和图7可以看出,在阀芯凹角附近和出口管路沉割槽处总有高速度和高湍流强度。湍流动能(Turbulent Kinetic Energy)表征湍流运动的严重程度,其值越大,湍流脉动的长度和时间尺度就越大,能源损耗越大。

为了量化阀口处的湍流强度,沿着湍流动能变化较大处设置了一条监测线,监测y方向上的湍流强度变化情况,图8表示四种阀芯结构滑阀对称面上监测线的湍流强度,四种阀芯结构的滑阀内部湍流变化规律是相似的。结合图7和图8可以发现:油液在进口处湍流动能很小,基本上是以层流的形式进入滑阀,随后湍流动能逐渐上升;在y=15 mm附近迅速增大,出现第一个波峰,此时,流体流过阀芯,由于阀口节流作用,形成剧烈的湍流,导致湍流强度迅速增加;随着流体逐渐流出阀口,湍流强度缓慢减小;在y=17～18 mm 处出现第二个峰值,这是由于高速射流流出阀口不断撞击阀颈,导致流动混乱,湍流强度增加;流体沿着阀颈流出,随着与阀口距离的增加,湍流强度逐渐减小。

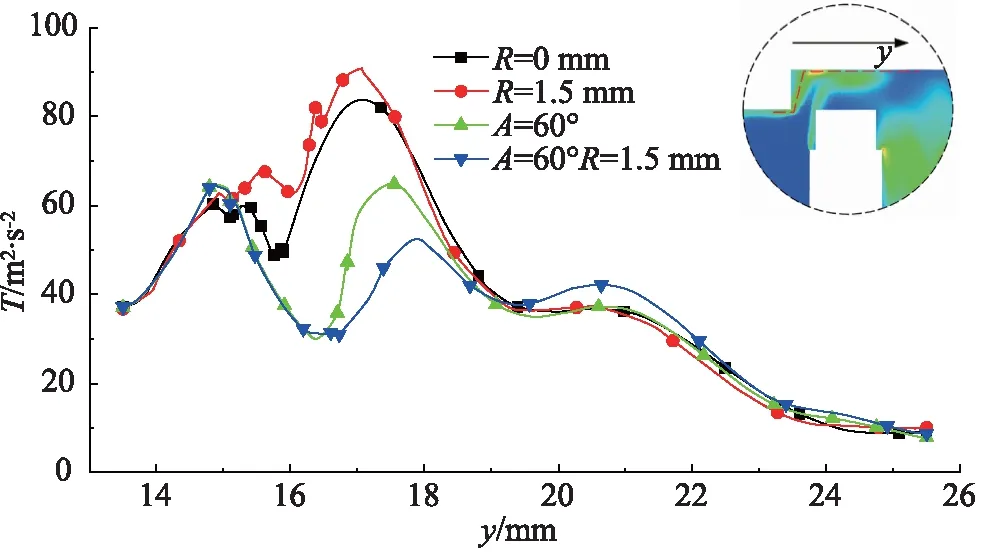
图8 四种阀芯形状的滑阀监测线上的湍流动能

阀芯形状的影响主要体现在阀颈部分,可以看出,“斜边+弧边”形滑阀内部的湍流强度普遍低于其他三种结构。这是因为高压流体流经阀口时斜线结构起到引流作用,圆弧形结构起到了缓冲作用,改善了阀体中的涡流,因此阀颈处的湍流强度比其他结构有所降低。

4 滑阀阀芯凹角结构优化

通过CFD分析发现“斜边+弧边”形阀芯结构可以有效抑制阀口处的漩涡,降低阀口区域的湍流强度,提高能量利用效率。以液压滑阀能量损失特性作为评价目标,通过Kriging代理模型构建液压滑阀阀口湍流动能与阀芯凹角结构参数之间的函数关系,利用粒子群算法对凹角结构组合进行优化设计。

4.1 最优拉丁超立方试验设计

由于决策变量与优化目标间的函数关系未知,需要以试验设计的方法,在决策变量的设定范围内进行抽样。构建以阀芯结构尺寸(斜线角度A,圆弧半径R)为自变量,能量损失特性(湍流动能T)为因变量的样本空间,在这个样本空间进行近似模型拟合。

常见的试验设计方法有正交数组、拉丁超立方设计、最优拉丁超立方设计等。最优拉丁超立方设计(Optimal Latin Hypercube Design,OLHD)改进了随机拉丁超立方设计采样的均匀性,使因子和响应的拟合更加精确真实,具有非常优秀的空间填充性[14-15]。选用OLHD对决策变量进行采样,设置样本点个数为25,决策变量的取值范围为:A=55°～70°,R=0～3 mm,图9为OLHD采样生成的散点。

图9 最优拉丁超立方抽样结果散点图

4.2 Kriging近似模型构建

Kriging近似模型方法是以变异函数理论和结构分析为基础,在有限区域内对区域化变量进行无偏最优估计的一种方法,因此又被称为空间局部插值法,广泛应用于工程领域。在优化设计过程中,可以通过已知点的数据对未知点进行预测,且估计方差最小,大大提高了优化设计的效率。

设x0为未观测待估值点,x1,x2,…,xN为其周围近的观测点,对应的观测值为y(x1),y(x2),…,y(xN)。

此处,λi为待定加权系数,准确计算权重系数是Kriging插值的关键。其必须满足两个条件:

(1) 无偏估计,设估值点的真值为y(x0)。由于模型的空间变异性,y(xi)以及y(x0),y(x0)均可视为随机变量。当为无偏估计时:

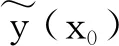
(12)

其中,γ(xi,xj)表示以xi和xj两点间的距离作为间距h时参数的半方差值,γ(xi,x0)则是以xi和x0两点间的距离作为间距h时参数的半方差值。

基于OLHD采集的样本点,通过Kriging插值方法拟合数据样本点,进而构建近似模型。借助平均相对误差(Average<0.2)和可决系数(R-Squared>0.9)来权衡模型的精度[16],误差分析表明建立的Kriging近似模型的平均相对误差为0.0614,可决系数为0.9552,拟合度较优。图10为湍流动能T的近似模型。

为了进一步保证近似模型的可靠性,对参数随机取一个值,将Fluent仿真计算得到的数值与Kriging近似模型预测值作比较。取A=63°,R=1.95mm,Fluent分析得到阀口处最大湍流动能为66.41m2/s2,Kriging模型预测值为65.95m2/s2,误差大约为0.69%,预测精度较高。

4.3 粒子群算法优化

粒子群算法通过群体中个体间的相互协作与信息共享实现智能寻优,广泛应用于函数优化、结构设计等领域。利用粒子群算法对滑阀阀芯组合结构的Kriging模型进行优化求解,选取粒子数即决策变量为粒子群算法中的粒子个体,以目标函数为粒子群算法中的适应度函数。

以斜线角度A、圆弧半径R为决策变量,最大湍流动能为目标函数,优化迭代500次后得到最优解,粒子优化迭代如图11所示。通过Isight相关性图对决策变量进行相关性分析,斜线角度A与湍流动能T呈正相关,相关系数为0.35,圆弧半径R与湍流动能T呈负相关,相关系数为-0.2,斜线角度A的影响较大。

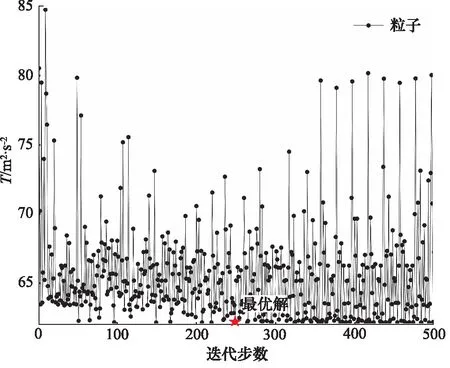
图11 粒子群优化粒子迭代分布图

采用多学科优化软件Isight的EDM模块查看目标函数对应解的分布状态,如图12所示。图中的每组线条表征优化目标函数的组合,可以发现目标函数的值在62.163～82.163 m2/s2间迭代变化,最终得到最优的滑阀结构参数组合为:斜线角度A=57.4°,圆弧半径R=1.14 mm,最大湍流动能为62.163 m2/s2。

图12 优化迭代取值

5 仿真验证

为了验证Kriging近似模型结合粒子群优化算法对滑阀结构参数优化的可靠性,将常规滑阀模型及粒子群算法优化结果进行CFD仿真计算,结果如表4所示。仿真值与优化值之间的误差为0.8%,粒子群优化结果可信度较高。

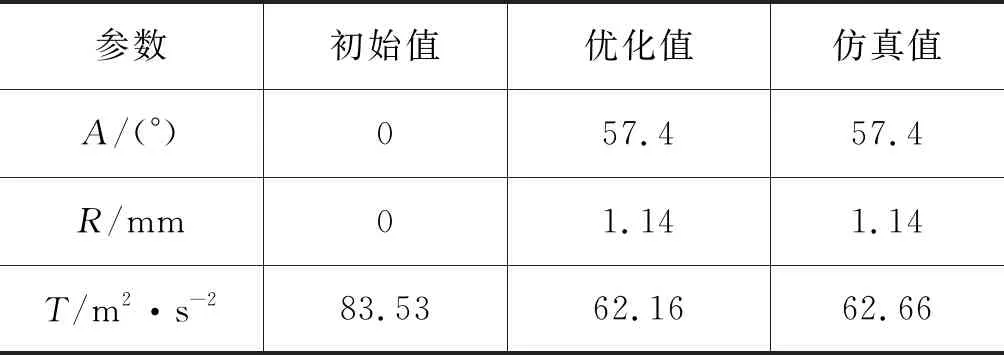
表4 粒子群优化结果对比

图13和图14为优化前后滑阀对称面上速度和湍流动能分布云图,图15为常规滑阀与结构改进滑阀对称面上监测线的湍流动能(监测线设置与图8湍流动能监测线一致)。阀口凹角处斜线角度和圆弧半径的变化对油液进出口流速、湍流强度及阀颈底部和阀体上部漩涡分布影响较小,但是极大改变了阀口处的流线和湍流动能分布,有效抑制凹角处漩涡的产生。常规滑阀湍流强度最大的区域分布在阀颈处为83.53 m2/s2,优化后最大湍流动能分布在凹角处为62.66 m2/s2,阀颈处的最大湍流动能为54.26 m2/s2,阀内最大湍流动能较常规滑阀减少约25%,阀颈处最大湍流动能降低约35%,大大提高了阀内能量利用率。

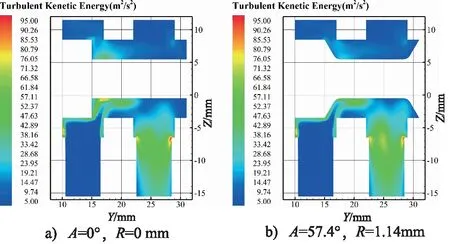
图13 滑阀对称面湍流动能分布云图

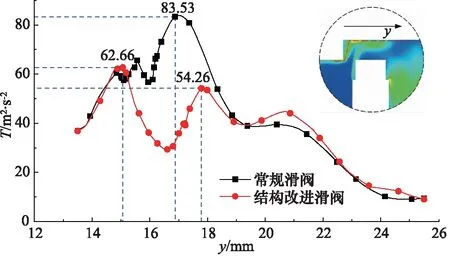
图15 滑阀监测线上湍流动能对比

6 结论

(1) 阀口开度、入口流量一定时,不同阀芯凹角的结构对滑阀内部的流场分布有显著差异,“斜边+弧边”形结构阀芯可以有效抑制阀芯凹角处漩涡的产生与发展,降低液流的湍流强度,提高能量利用效率;

(2) 基于阀芯凹角组合结构CFD仿真分析,将Kriging近似模型和粒子群算法相结合,应用到阀芯结构的优化设计中,得到湍流动能最小的阀芯结构参数:当斜线角度为57.4°,圆弧半径为1.14 mm时阀口区域最大湍流动能分布在凹角处为62.66 m2/s2,较常规滑阀降低25%。