运用通过耦合偏微分方程建立的高效热动力学模型(ETK-model)评估刹车系统中压力点的变化
袁博
(山西科腾环保新材料股份有限公司,山西 太原 030032)
1 简介
在火车刹车时,由于摩擦力作用于刹车片和刹车盘之间,刹车片将产生磨损,这种磨损是非对称的。在刹车过程中动能将转化为热能,热负荷会造成刹车盘的形变。非对称的磨损导致了摩擦力的变化以及摩擦面上压力点的变化,由于磨损造成的刹车片形变以及热负荷造成的刹车盘形变,等效压力点的位置将一直变化。
1.1 理论背景
刹车片是刹车系统中最为主要的部分,一般是由高摩擦力材料制成。摩擦力分为两部分:静摩擦力和滑动摩擦力。刹车片和刹车盘的材料特性影响着刹车系统中的磨损率。材料特性的变化会使磨损率产生很大的变化。材料磨损、工作性能以及寿命也都取决于材料特性。
刹车片由于其磨损问题需要定期更换,有些刹车系统会通过机车界面交互系统提醒驾驶员及时更换刹车片。为了解释非对称磨损,本论文将引入滑动磨损模型[1]。
通过引入阿查德磨损定律:
式(1)中:S为滑动距离;K为磨损系数;F为负载力;H为材料硬度。
磨损体积计算公式为:
刹车片内外部的滑动距离计算公式为:
当刹车片与刹车盘摩擦时将会在摩擦盘的内圈及外圈产生热负荷差,热力学模型将分为3 种情况讨论:内外圈热负荷差为零,外圈热负荷大于内圈热负荷,外圈热负荷小于内圈热负荷。这3 种情况的分析将借助软件ANSYS 来实现。
1.2 刹车盘和刹车片介绍
刹车盘、刹车片材料参数分别如表1 和表2 所示。

表1 刹车盘材料参数

表2 刹车片材料参数
2 高效热动力学方程数学模型的建立
高效热动力学模型(以下简称“ETK 模型”)的建立是本文的重点部分,本部分将介绍2 种基础ETK模型,在ETK 模型中有许多变量,需要通过定量研究法对这些变量进行分类。首先将悬挂现象分离,使用相对基础的模型进行模拟,然后刹车片两侧压力以及磨损百分比的曲线图要通过软件MATLAB 进行绘制,最后得出压力中心点的变化曲线。
2.1 基础ETK 模型构建
基础ETK 模型(刹车片侧视图)如图1 所示,通过骨架的构建,近似模拟刹车片在刹车时的磨损情况,Fv作用于悬挂系统与刹车片的连接处,产生压力,压力传导于刹车片的两侧。由于内外侧的半径不同,所产生的角速度不同,固滑动距离不同,产生不同程度的磨损[2-3]。
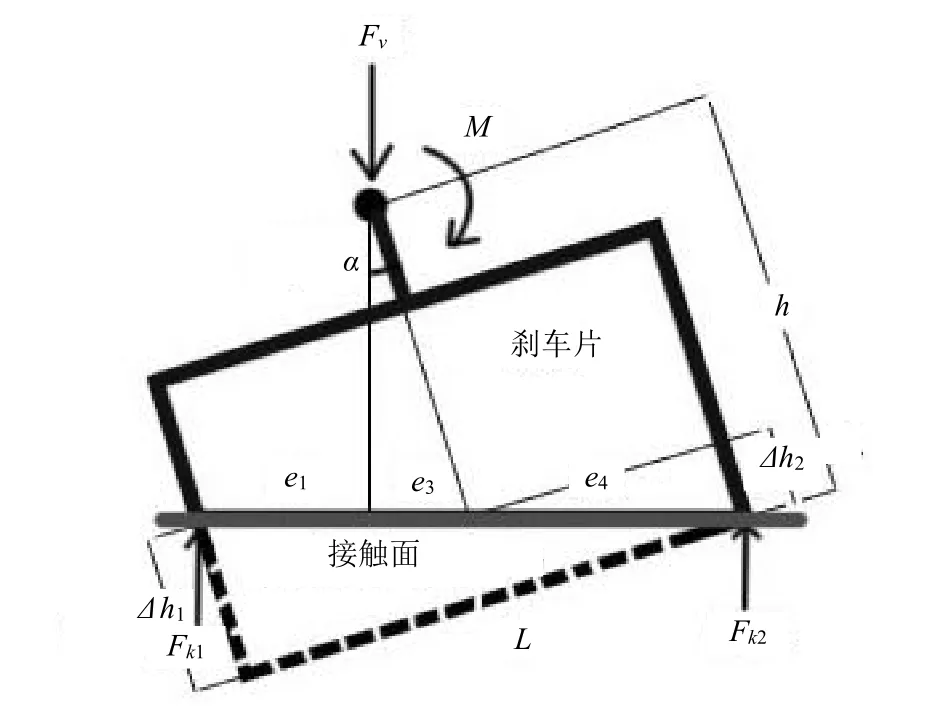
图1 基础ETK 模型(刹车片侧视图)
基础模型中提到了2 个作用效果:磨损效果和悬挂效果。在磨损模型构建中,角度α是最为重要的变量,角度α的变化率影响了磨损模型的所有应变量。同时在刹车盘上产生了热形变效果,在后面的内容里会进行详细说明,热形变产生的偏转角度为β,求β角的过程同样要用到偏微分方程。α角和β角同时发生变化,在刹车系统中被耦合,当α角变化的时候β角同时产生变化,下面将详细阐述这2 个角度发生变化时ETK 模型的变化。
2.2 不同情形下ETK 模型的构建
根据实际情况,本部分列出了6 种真实情形对应的ETK 模型。α角度的正负遵循以下规则:刹车片外侧磨损大于内侧,角度为正;反之,角度为负。β角度的正负遵循以下规则:刹车盘内侧面形变大于外侧形变时,角度为正;反之,角度为负。
根据之前定义的α角度以及β角度,真实情况下有以下6 种情况:
2.3 计算磨损体积
本部分将介绍如何计算刹车片上的磨损体积,α角通过内外侧磨损高度的差额来计算,通过刹车片上方的钢结构圆棒,压力传导于刹车片后,将刹车片分为内外2 部分,F1作用于A1,而F2作用于A2。本部分将通过对2 种形态的刹车片进行面积划分,得出对于这2 种刹车片α角度的变化量[3]。两种刹车片形态如图2、图3 所示,参数如表3 所示。

图2 第一种刹车片形态
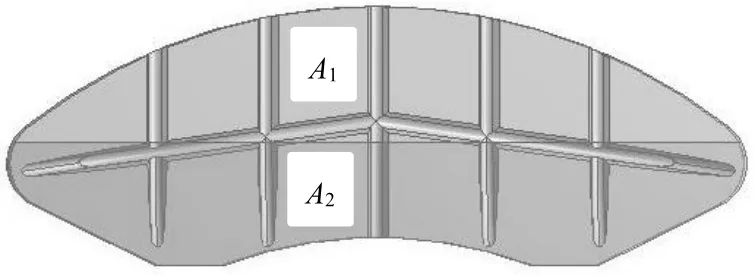
图3 第二种刹车片形态

表3 两种刹车片的参数
对于第一种刹车片形态,α角度的变化量为:
对于第二种刹车片形态,α角度的变化量为:
2.4 构建磨损角度及力矩的关系
由于刹车片内外侧磨损的不对称性,将在上表面和XY面产生一个角度。悬挂系统将限制由于摩擦不均衡而产生的角度,目的在于控制刹车片内外侧的磨损差额不至于过大。悬架模型将导入到软件ANSYS 中,通过分析数据得到磨损角度和力矩的关系[4]。
根据ANSYS 中的分析结果,设定力矩由0 Nm 逐步增加到5 600 Nm,每个步长增加800 Nm。收集每个步长下角度的变化值,从而得到磨损角度与力矩的关系。
通过MATLAB 中拟合函数工具对所得数据的分析,得到以下公式[4]:
2.5 热形变角度的构建
本部分将主要描述如何通过公式构建出由热形变导致的角度β。刹车盘外部平面与内部平面产生热负荷差额,通过内外部热负荷梯度可以计算得到角度β。当内外侧热负荷相等时,刹车盘同样会产生热形变。所以对角度β的计算包含2 个部分:第一部分是关于热负荷梯度的,第二部分是当热负荷梯度为0 时,刹车盘的热形变量。通过下面的公式[5]得出角度β:
式(2)—(7)中:Φ为机械能转化为热能的转化效率;η为刹车片上的热分部;μ为摩擦系数。
这里仍然有2 个未知的系数a1和a2,这2 个系数将借助软件ANSYS 以及MATLAB 中的拟合函数求得。
刹车盘内外两侧有温差时在ANSYS 软件中的分析结果如图4 所示。第一次模拟代表了等式中热负荷梯度的部分。第二次模拟中热负荷梯度为0。因为在模拟中求得的是热偏转角度和温度的关系,但在MATLAB 编程中热偏转角度是与2 个接触面的摩擦力有关的,换言之是与热能相关的,所以还需要得出热能与温度的关系。

图4 刹车盘内外两侧有温差时的分析图
外部盘的温度变化由100 ℃升高到900 ℃,内部盘温度变化由900 ℃降低到100 ℃。两边相加和为1 000 ℃。每步长为100 ℃。图中圆孔的位置在模拟时将被固定。通过MATLAB 中拟合函数模块得到[4]:
式(8)中:β为圆锥角角度;TGrad为温度梯度。
公式中包含常数部分,当刹车盘内外两侧温度均为500 ℃时,等式前半部分为0,偏转角为0.038 4 rad(弧度制)。
刹车盘内外两侧温度相等时在ANSYS 中的分析结果如图5 所示。通过此分析结果可以得出内外侧温度相等时温度和等式常数部分的关系。
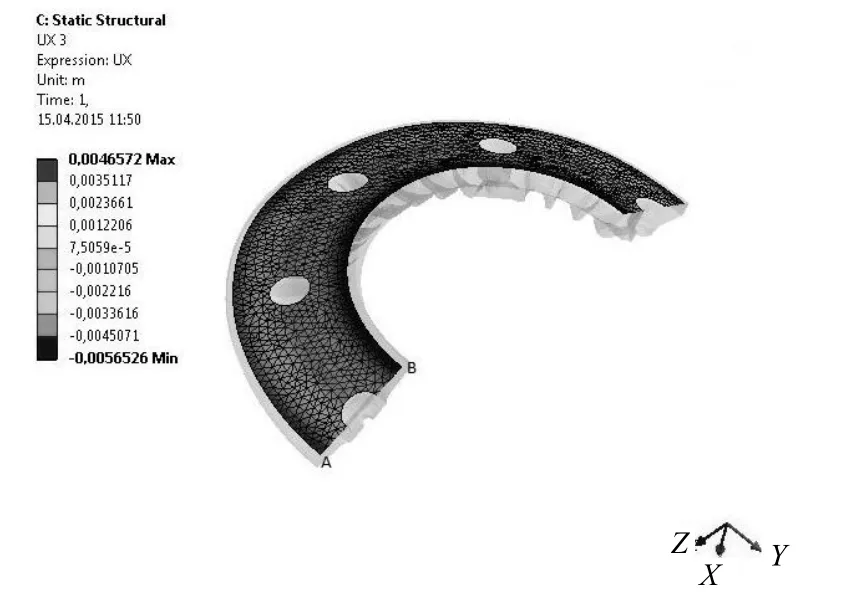
图5 刹车盘内外两侧温度相等时的分析图
外侧盘温度由100 ℃升高到1 000 ℃,内侧盘的温度变化同样。固整体刹车盘温度由200 ℃升高到2 000 ℃。通过MATLAB 中拟合函数模块得到:
式(9)中:T为温度。
本式中温度为0 时仍有常数部分,此为环境中温度影响的形变。
由于圆锥角角度,即文中提到的热形变角度,在现实中会受到许多因素的影响,本文只是近似地考虑一些影响因素,并通过在ANSYS 软件和MATLAB 软件中的模拟得出现象的相似等式,如果需要得到更精确的变化,则要在真实刹车情况下对刹车盘进行大量的数据采集,最后通过热能和温度的公式Q=cmT进行计算。
上面提到的刹车盘被分为外部圆环和内部圆环2部分。外部圆环的质量为m1,内部圆环的质量为m2;外部圆环上热能为Q1,内部圆环上热能为Q2,比热容c=450 J/(kg·K)。从而得出以下等式[5]:
通过在软件ANSYS 中对刹车盘进行取值得到刹车盘密度为7 850 kg/m3。外部圆环的体积V1=7.393 8×10-3m3,内部圆环体积V2=2.482 1×10-3m3。通过对公式(8)—(12)的耦合,可以得出最终热偏转角度的表达式:
2.6 构建压力点位置
压力点产生效果后,压力被分解为刹车片内外部的等效反作用力点。通过本论文所述部分得到的磨损量产生的角度α以及由于热形变产生的角度β的等式关系,可以在MATLAB 中通过耦合偏微分方程迭代模拟整体刹车系统的变化趋势,初始状态需要在ANSYS中进行模拟后得出。
3 刹车系统在MATLAB 软件中的模拟结果
在压力点的研究中,本文选取了2 种刹车片形态,即第一种形态和第二种形态。在MATLAB 软件的模拟过程中,将时间作为自变量设定。时间设定从0 到60 s,步长设定为0.000 5 s。行驶速度从200 km/h 降低到0。轮子直径为1.2 m,角速度通过计算为93 rad/s。在磨损角度(α角)的模拟中,系数K设定为1.0×10-7,此数值由实验室实验所得。
刹车片一和刹车片二压力点变化趋势分别如图6和图7 所示。其中,点1 为刹车片外侧的压力中心,点2 为刹车片内侧的压力中心,当总压力中心为正值时,代表总压力点位于刹车片内侧,反之位于外侧。
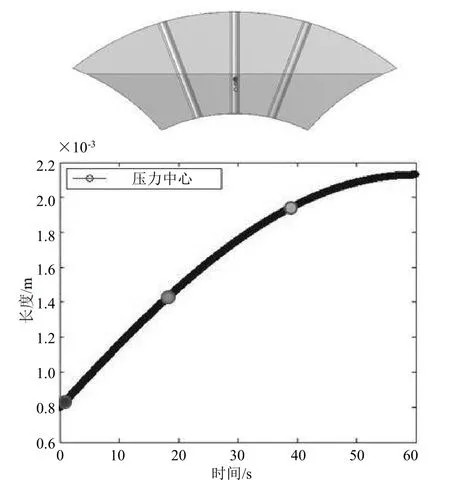
图6 刹车片一压力点(点1)变化趋势
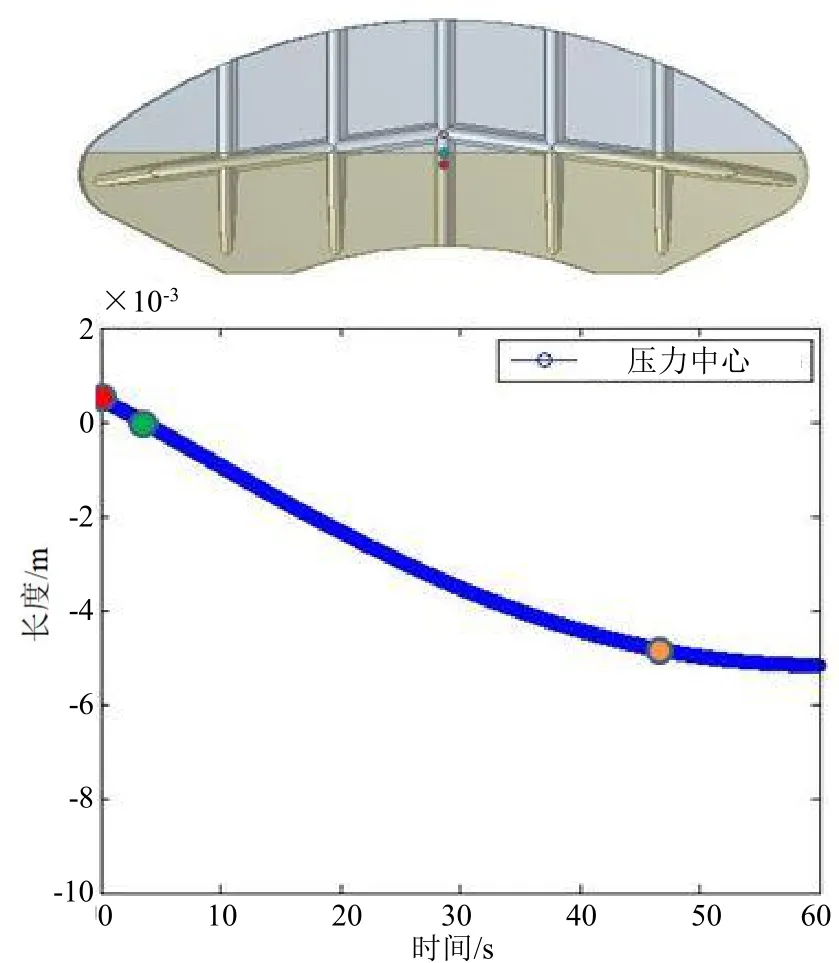
图7 刹车片二压力点(点2)变化趋势
通过以上各图可以得出,磨损以及热形变在2 种不同形态的刹车片上所表现出的差别。对于第一种形态的刹车片来说,内侧的压力百分比总是大于外侧,并且差额越来越大。对于第二种形态的刹车片,在大约前3 s 的时间里,内侧的压力百分比较大,但是在3 s 后外侧的压力百分比将超过内侧,并且差额越来越大。这种压力分配的不同现象造成了总压力中心在2种刹车片上的移动方式也不同。在刹车片一的接触面上,总压力中心总是偏向于内侧并且一直向更内侧移动,而对于刹车片二来说,总压力点首先位于内侧,随着时间的变化却逐步向外侧移动。
4 结束语
本文主要研究了刹车系统的运作过程。在刹车过程中产生了2 种现象,即非对称的刹车片磨损现象以及由摩擦产生的刹车盘热负荷形变现象。通过近似的数学建模,研究了这2 种现象的变化过程以及对刹车系统产生的影响。为了研究此类现象,本文选择了运用耦合偏微分方程对高效热动力学模型进行构建。
在本文的第二部分,详细描述了ETK 模型是如何构建的过程。首先,建立了2 种基础模型,并对这2种模型进行受力分析以构建出磨损角度α和压力之间的关系,而后根据分析得到不同的6 种数学模型,并对每一种情况进行等式建立。对磨损过程进行分析后,开始对刹车盘上的热负荷形变进行模型建立,在此过程中借助了软件ANSYS 中的一些数据,以及通过MATLAB 拟合函数的运用,得到热偏转角β的表达式。而后对2 种现象进行耦合,设定初始值以及步长后,在MATLAB 软件中进行模拟,得到刹车片一以及刹车片二接触面上总压力点的移动图。

