云计算数据中心的虚拟资源自适应供给模型

李晖,严文,刘文亮,杨晓东,胡雯,欧俊龙,唐雨晨,林章岁,梅超

(1.福建省电机工程学会,福建 福州 350013;2.国网福建省电力有限公司,福建 福州 350003;3.清华海峡研究院(厦门)智慧能源研究中心,福建 厦门 361010;4.国网福建省电力有限公司经济技术研究院,福建 福州 350013;5.国网厦门供电公司,福建 厦门 361012)

0 引言

云计算数据中心作为在“东数西算”[1]等国家重大方针政策背景下极为重要的数据处理基础设施,在广泛的产业和商业应用中占据不可替代的位置[2].因此,如何优化云计算数据中心的资源利用调度,让中心的处理能力得到最大化的应用,成为目前研究的热点课题.

加州大学伯克利分校在其2009年发布的云计算白皮书[3]中指出,“弹性”平台可动态进行计算能力的分配,这是云计算平台的重要属性之一.在使用弹性云平台时,用户无需担心因计算资源分配溢出而产生不必要的开销,或因资源不足而导致服务能力受到影响,可更加专注于本身的业务需求.

弹性资源需要根据用户的线上使用情况进行动态分配.因此,在弹性平台的构建过程中,弹性资源的供给方式是目前需要考虑的重要问题.为此,需要探究负载情况与服务能力之间的数学关系,以此为基础构建相关的数学模型,从而对用户使用期间的资源利用情况进行感知,最终给出合理的计算资源分配方式.这一实践过程便是本研究的研究思路.

在计算虚拟化的当下,云平台虚拟机的调度是弹性的主要来源[4].运营商可通过合理分配虚拟机,综合分析平均响应时间、成本等各种因素,合理优化虚拟机的设置,减少云计算在数据中心的数量功耗.在虚拟机调度和虚拟机动态集成两个方面,实时调整虚拟机分配策略,使资源利用率更高、响应时间更快、能耗更低[5-7].在虚拟机的调度方面,目前已取得许多研究成果.有学者使用启发式算法[8-9],通过监控利用率来指导虚拟机的调度过程.使用排队论方法进行虚拟机调度亦有先例,可使用单队列排队模型[10-11]和多队列模型[12]进行建模.

本研究提出一种基于排队论的多层结构虚拟资源自适应供给模型,在保证服务质量的基础上,以降低计算资源的使用成本为导向,进行资源调度优化,通过调度多层虚拟机的排列,提供一个效率较高的虚拟资源调度方案.

1 虚拟资源自适应供给模型

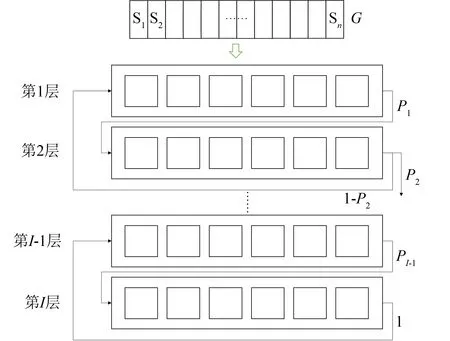
图1 层次模型结构示意Fig.1 Schematic diagram of hierarchical model structure

基于多任务且负荷变动相对较小的情景,建立模型,模型结构如图1所示.实际上,云计算数据中心应为1个多进单出队列的I层处理平台结构.为方便整体描述网络模型,以1个单入单出队列表示处理平台的队列.共有n个会话(S1～Sn)同时向云计算数据中心发送请求,每个会话可理解成1个独立的用户,请求总数为G.在概率空间中,Pi表示从第i层跳到第i+1层的概率,其初始值可以任意设定.来源于第i层后层已处理过的请求,则会以1-Pi的概率跳到第i层的前一层,即i-1层.

1.1 层次模型构建

为对模型进行简化,可将虚拟机的实例抽象为两种,即大型实例(L)和小型实例(S),以此模拟在实际使用中处理能力较强的虚拟机和较弱的虚拟机.在实践过程中,为合理调配虚拟机资源,通常将这两类处理能力与价格均不同的虚拟机混合使用,以期获得更好的资源分配效果.

假设在当前阶段数据中心第i层运行的大型和小型实例虚拟机对第i层发出请求,经过负载均衡器后,每个虚拟机请求的平均到达率为

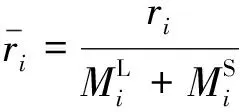
(1)

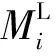
根据多层跳转模型,第i层的到达率可用其前后两层的到达率表示为

ri=ri-1,i+ri+1,i

(2)

式中:ri-1,i表示第i-1层到第i层的到达率;ri+1,i表示第i+1层到第i层的到达率.

特别的,第1层会话输入的到达率为

r0,1=G

(3)

最后一层(即第I层)的到达率等于其前1层的离开率(DI-1,I),即

rI=DI-1,I

(4)

对于单个虚拟机实例,可将其视为一个有限排队空间的排队实体,即M/M/1/K/∞/FCFS型排队模型.K为单个虚拟机的最大队列长度;M表示将顾客到达的分布和服务台处理的分布视为指数分布.根据排队论公式,可得

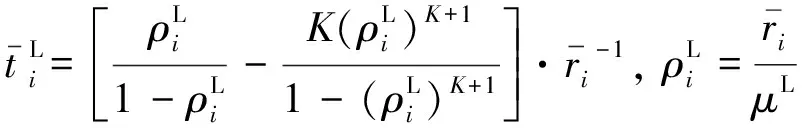
(5)

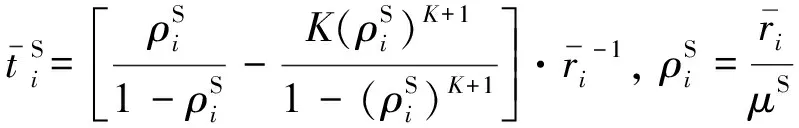
(6)

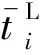
此时,第i层的离开率为

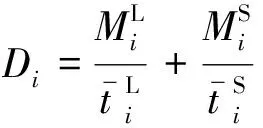
(7)

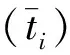
根据到达率和跳转概率的定义,可得

ri,i+1=Di·Pi

(8)

ri,i-1=Di·(1-Pi)

(9)

1.2 平均等待时间求解

采用递推方式,计算任意层(第i层)的平均等待时间.

对于最后一层(即第I层),将式(5)、(6)带入式(7),可得

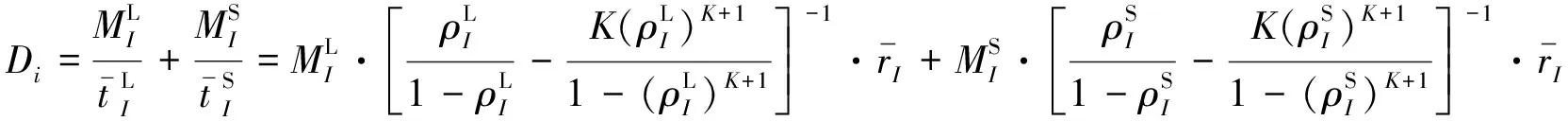
(10)

(11)

考虑第I-1层,根据式(2)可得

(12)

根据式(8)可得

rI=DI-1·PI-1

(13)

DI-1=gI-1(rI-2,I-1)

(14)

上述类推可反复运用,即

Di=gi(ri-1,i)

(15)

类推至第一层,根据式(3),可得

D1=g1(G)

(16)

1.3 约束分析

记最远到达第i层的请求数量为Gi,则对于最远到达第i层的请求而言,其平均遍历时间为

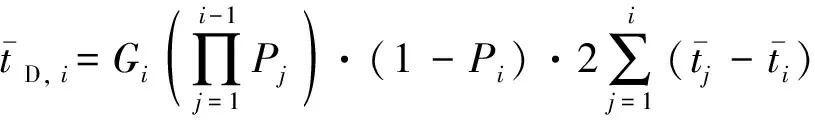
(17)

由此,可得出总的平均遍历时间为

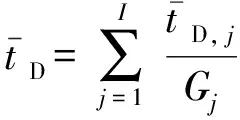
(18)

以CL和CS分别表示单个大型和小型实例虚拟机的花费,则总花费为

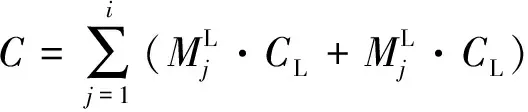
(19)

至此,可将调度问题转化为约束优化问题,即求最小的总花费(Cmin),满足

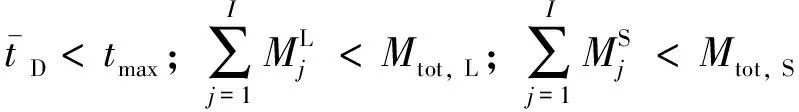
(20)

式中:tmax为约定的系统最大响应时间;Mtot,L和Mtot,S分别为大型和小型虚拟机的总数.

1.4 初始参数估计

1.4.1跳转概率

跳转概率可通过在线观察长时间内从第i层跳到第i+1层请求的总量和第i层申请的总量,得出其取值范围.在这之前,每个Pi的初值可以先设置为0.5.

1.4.2虚拟机实例的服务能力

为得到模型中两种实例实际处理能力值的和,可构建简易离线测试平台,对两种虚拟机的服务能力进行观测.在服务较多时,虚拟机会出现线程竞争的问题,实际服务能力与服务数量相关.因此,需要在不同负载下,对两种实例进行仿真测试,以确定其实际处理能力值.

1.4.3虚拟机实例的成本

对于大型与小型实例虚拟机,实际应用时可以使用服务提供商的报价作为参数,而推导模型时参考Azure基础结构即服务的虚拟机定价进行估算.实验中,所采用大型实例的成本为0.037美元·min-1,小型实例的成本为0.020美元·min-1.

2 实验概况

2.1 实验配置

配置上选择微软Azure云计算平台[13]作为实验平台.为模拟多层的数据模型,使用RUBiS作为负载测试程序[14],使用 Matlab对约束进行求解.

2.2 实验数据

采用1998年世界杯官网首页某1 h的访问数据作为实验的负载配置[15],模型中的最大响应时间(LIMIT)设定为10 s.

2.3 对照算法

目前,基于利用率感知的虚拟机调度算法广泛应用于虚拟机调度中.该算法采用一种直观的、基于利用率感知的算法作为对照算法.以R表示利用率,则有: 1) 模型的每一层至少包含1个虚拟机小型实例;2) 当模型某一层满足R>95%时,添加1个虚拟机大型实例;3) 当85%≤R≤95%时,添加1个虚拟机小型实例;3) 当R<45%时,移除1个虚拟机大型实例;4) 当 45%≤R≤60%时,移除1个虚拟机小型实例.

基于利用率感知的算法在直觉上较为合理,同时调度算法容易实现,许多资源平台可采用此算法进行资源调度.

3 实验结果与分析

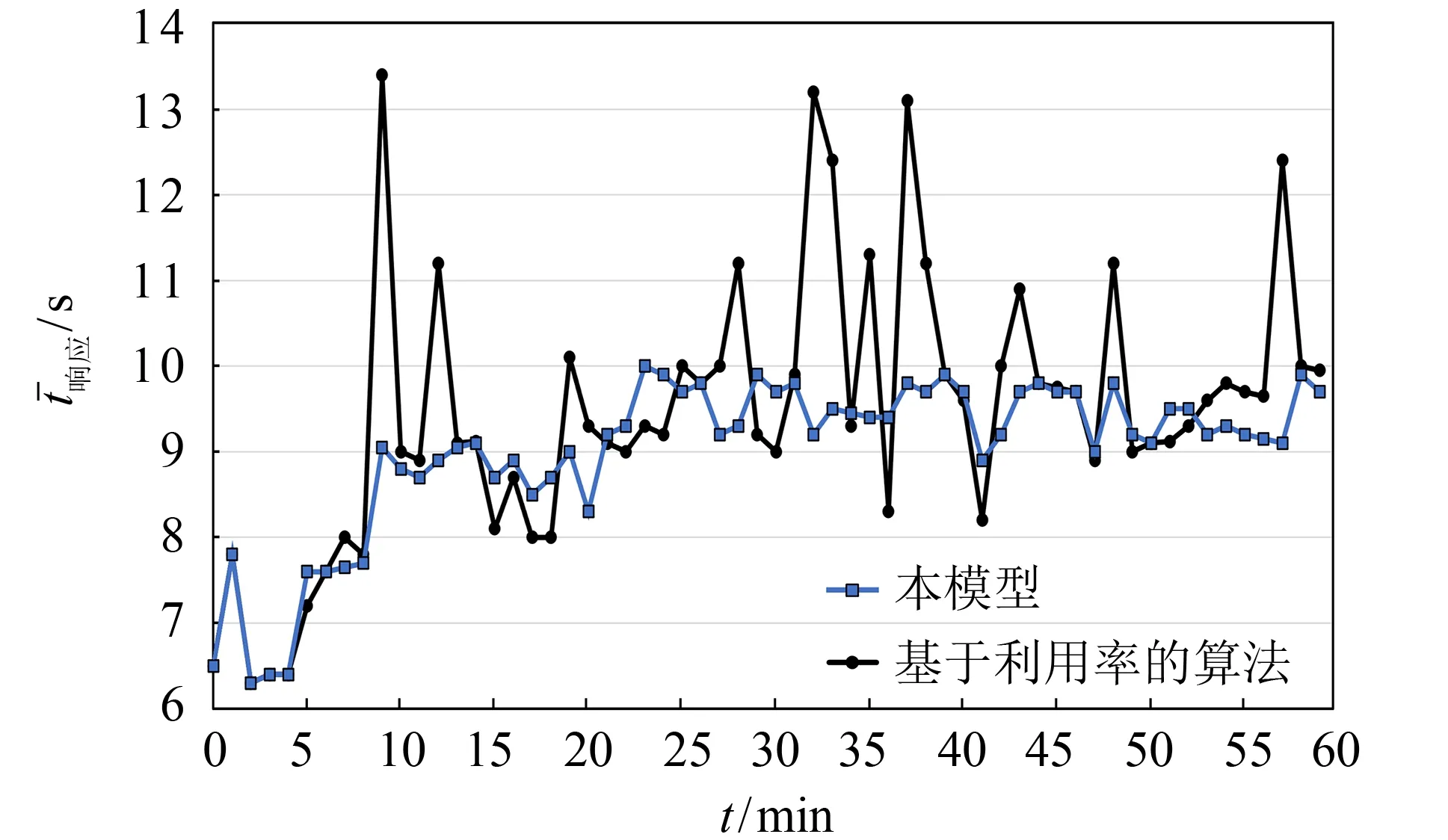
图2 本模型与基于利用率的算法响应时间对比Fig.2 Response time comparison between this model and the algorithm based on utilization

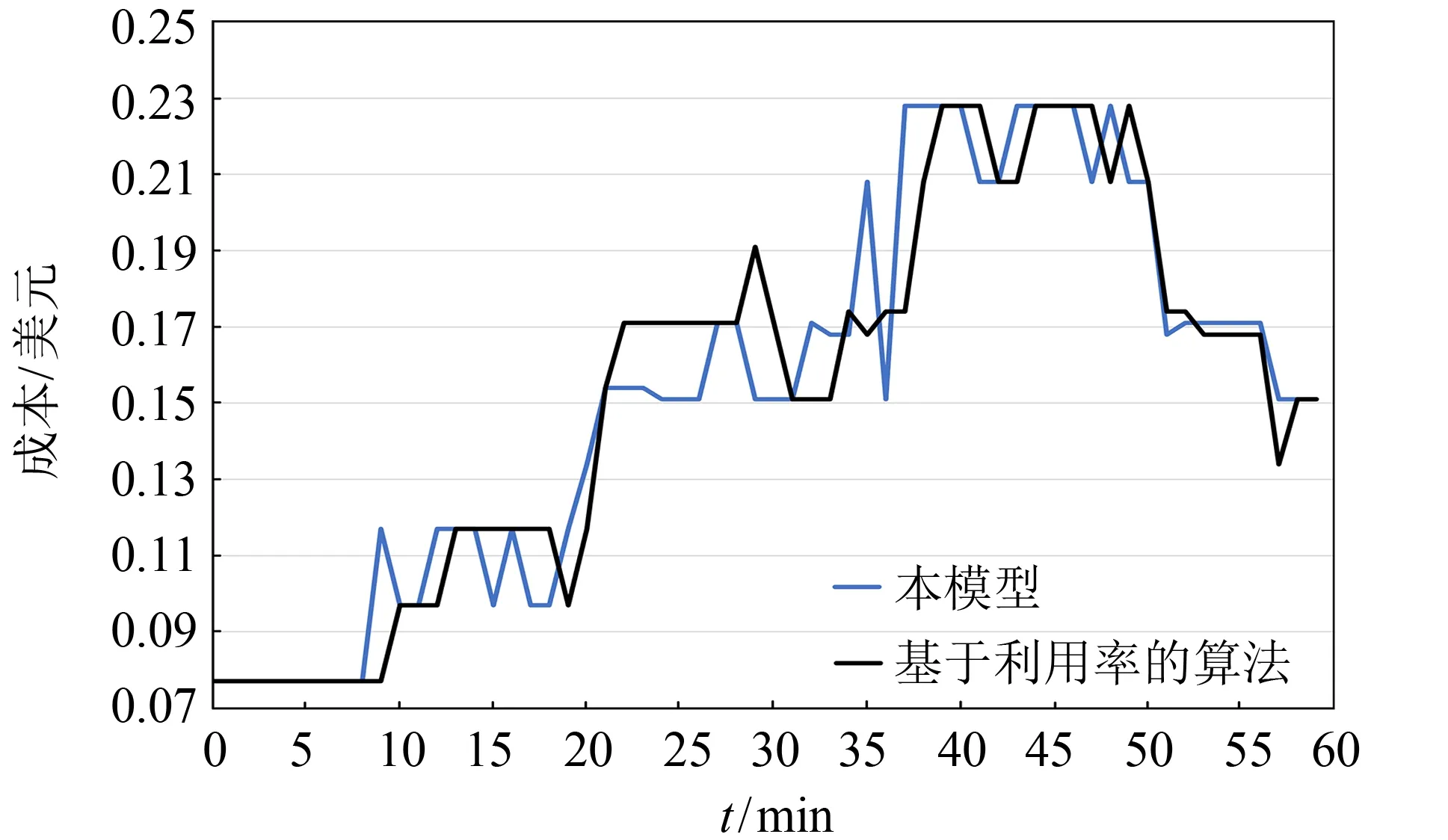
图3 本模型与基于利用率的算法成本对比Fig.3 Cost comparison between this model and the algorithm based on utilization

可以看到,与利用率感知的算法相比,本模型在平均响应时间与响应时间波动上有较好表现.在计算约束时,引入最大响应时间这一变量.因此,在实际应用时,采用本模型进行调度的过程中,所有时间段的平均响应时间均未超出最大响应时间.与利用率感知算法相比较,本模型的响应时间波动和平均响应时间均较小.

本模型在成本降低方面也有更好的表现,尤其是在负载快速上升的过程中,本方法有较小的总成本与成本波动.最终总成本也较为低廉,与基于利用率算法的成本对比降低0.5%.

4 结语

建立一种基于排队论的多层结构云计算数据中心的虚拟资源自适应供给模型,其核心思想为根据多层服务中每层的响应时间,动态地对虚拟机分配进行约束优化,以此达到降低总成本的目的.通过与传统利用率感知的算法进行对比,本模型在成本控制与虚拟机使用量方面均更具优势.优化约束使得请求的平均响应时间满足服务层次协议的约定,在保证服务质量的同时达到控制成本的目的.本模型的应用价值经过仿真测试的验证,可为实际云平台弹性调度方面的研究提供指导思想.