基于改进遗传算法的农产品物流配送模型研究①
汪 晔
(安徽商贸职业技术学院,安徽 芜湖 241000)
0 引 言
在物质经济水平不断提升的背景下,人们对安全、绿色的农户品的需求逐渐提高。因此,农产品物流配送问题成为如今诸多领域学者共同探讨的话题。相较于大多数发达国家,我国农产品采摘、运输等环节的损耗率处于较高水平,损耗率数值高达30%。现阶段国际农产品物流模式的主体为农协的县协组织和全国性组织,以及基层组织[1-3]。针对农产品物流模型,国内外大多数学者已经采用遗传算法等启发式算法对其进行求解,但模型的求解结果并没有获得物流企业和客户等多方面的认可。研究构建了一种农产品物流配送模型,并提出一种优化的遗传算法对其进行求解,旨在为电子企业物流配送的创新提供技术支持。
1 农产品物流配送模型及求解
1.1 农产品物流配送模型
农产品物流配送车辆路径问题可视为一种常见的组合优化问题,其分析的是在客户需求和地理位置确定的情况下,通过数学模型生成成本最低的车辆路径。图1是指农产品物流配送路径问题的示意图。该问题可以结合时间窗的车辆路径问题来分析[4]。因此,农产品物流车辆配送路径问题可视为带有软时间窗的车辆路径规划问题。软时间窗并没有对时间有较高的要求,它可允许运输车辆在时间窗外到达。但当车辆提前到达预约地点,则会存在等待成本;否则将会出现惩罚成本。式(1)是指成本函数。
(1)
式(1)中,在服务客户i时,车辆k由于时间窗约束而导致的损失。车辆k到达客户i的时间点,客户i的时间窗为[T1(i),T2(i)],T1(i)和T2(i)分别是指用户i最早时间和最晚时间,分别是指车辆提前到达或延时到达的单位等待成本值和单位惩罚成本值。sik={0,1},当sik的取值为1时,则表明车辆k能给客户提供配送运输服务;而当sik的取值为0时,则表明车辆k无法为客户提供配送运输服务。车辆路径问题的构成要素可分为目标函数、运输网络、约束条件、客户、配送中心、运输货物、运输车辆。
物流配送系统中,配送中心可以为一个或者多个,配送中心的位置也具有随机性。对于配送中心而言,配送货物既可以是单种类,也可以是多种类的,同时它所供应的货物既可以满足部分客户的要求,也可以满足所有客户的需求。图2是指物流配送中心选址的因素,主要包括交通状况、经济效应、环境因素、其他因素等。客户是需求及部分约束条件的制定者,也是车辆路径问题中需考虑的重要因素。这里面包括最大载重约束、特定货物的到达和取走时间等约束条件。约束条件如下所示,符合客户对货物品种、质量、数量的限制;符合客户对货物到达时间的要求;实际载重得不低于核载的重量。运输网络是指车辆路径问题中所需关注的主要因素,运输网络由无向边、有向弧、顶点组成。农产品物流车辆配送问题的目标函数为配送总体成本最小、客户对配送服务满意度高、运输车辆配送所行驶的距离最小、参与运输的车辆最少。
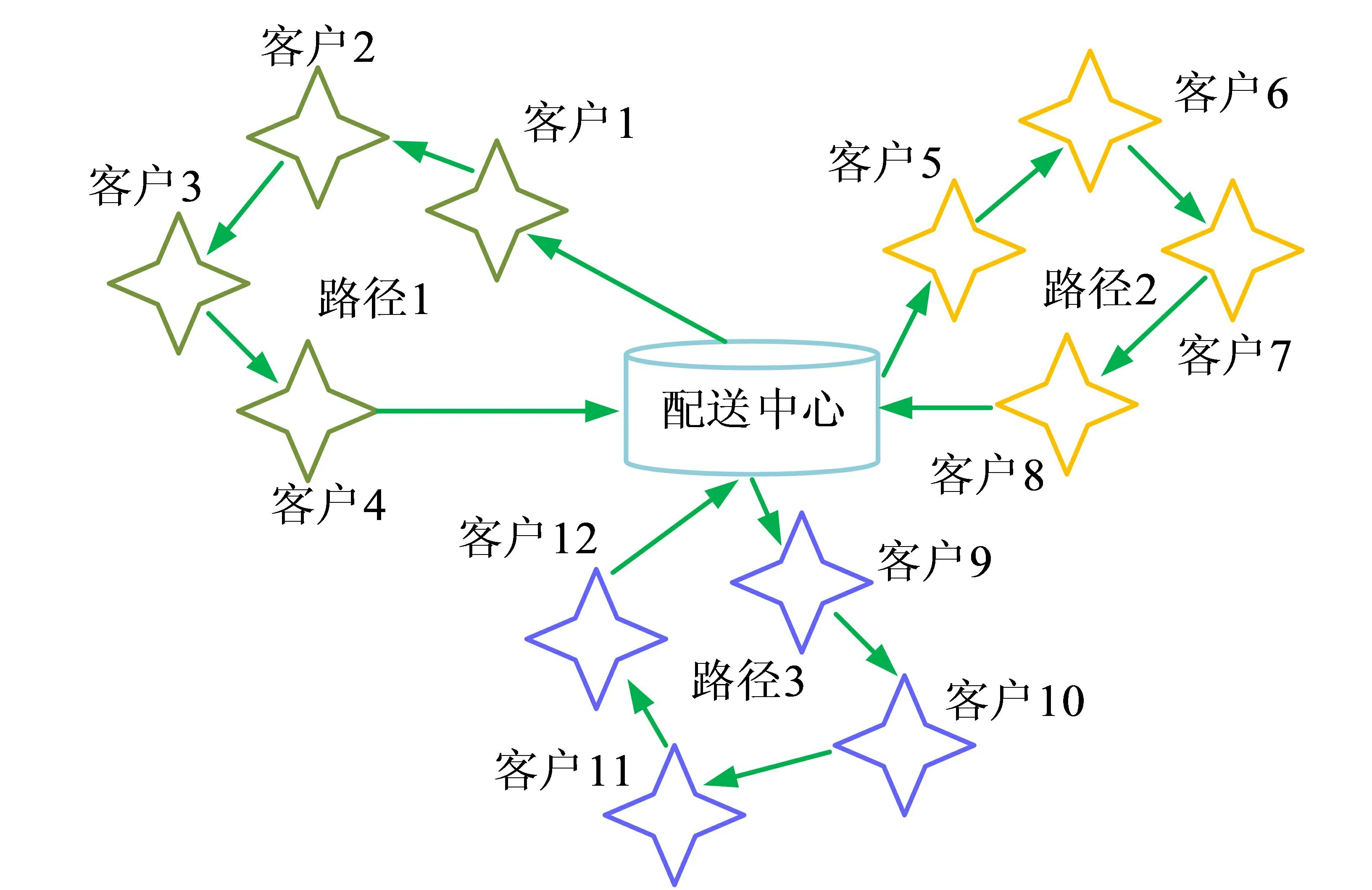
图1 农产品物流配送路径问题的示意图
总成本包括车辆的运输成本和时间成本,其中运输成本包括行驶总成本。时间成本具体为运输车辆延时到达的惩罚成本和提前到达所需的等待成本。式(2)是指目标函数的计算表达式。
(2)
式(2)中,客户数量和运输车辆的数目为n和m,配送车辆的单位距离成本和单位启用成本分别为α和β,cij是指客户i和j之间的距离,xijk是指客户i和j是否由车辆k配送。
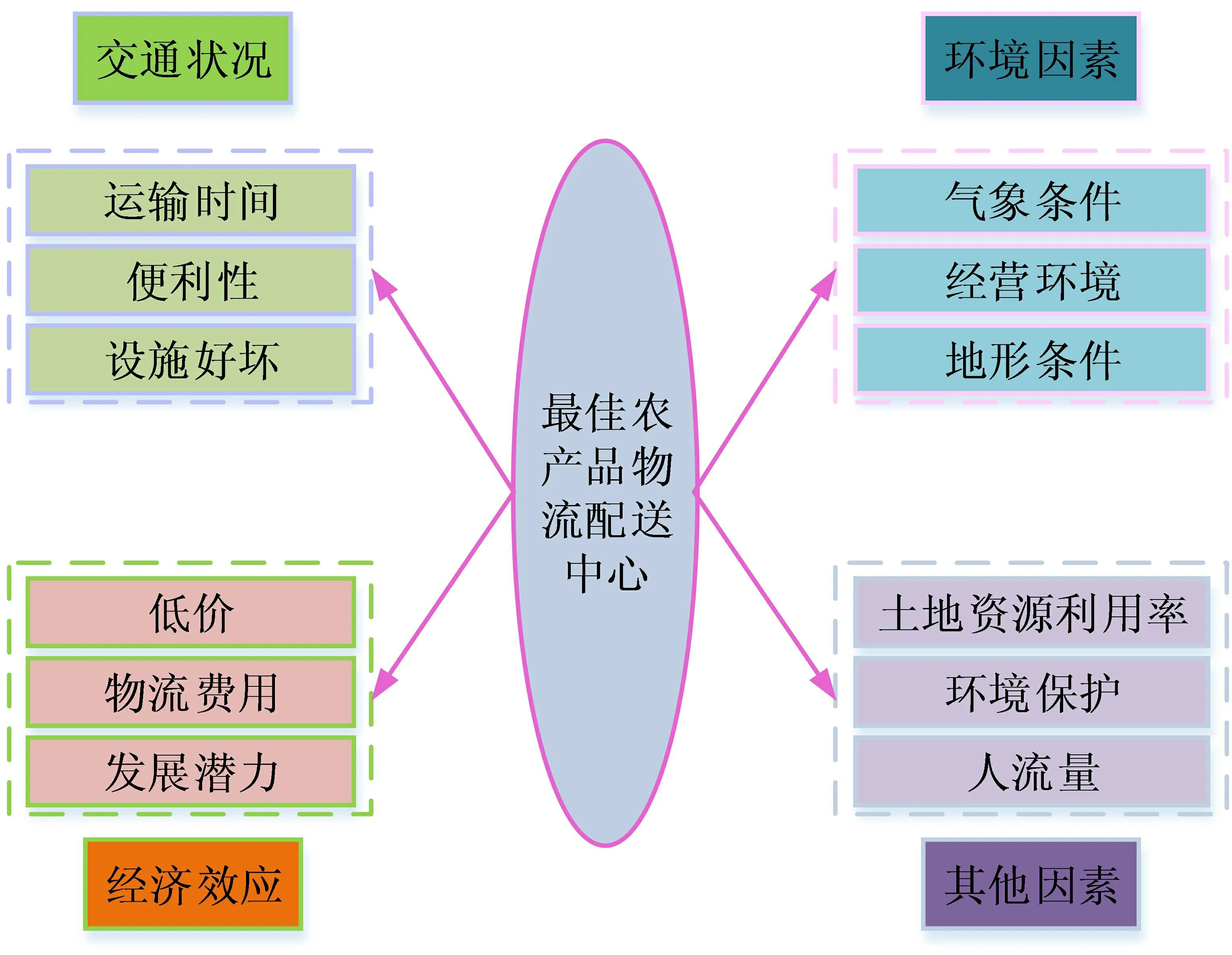
图2 物流配送中心选址的因素
1.2 改进遗传算法求解
针对农产品车辆配送问题,常见的求解方法为精确算法和启发式算法。遗传算法具存在初始解随机化、收敛速度慢、局部最优解等问题。研究针对这些问题进行了改进,图3是指改进遗传算法的示意图。首先依据农产品物流配送模型的特点,编码方式选择整数编码。然后根据客户服务的优先级别和影响因素确定存在解集的初始种群。其次,依据不同的目标函数确定相应的适应度函数,并利用适应度确定个体的遗传几率。再者,采用精英保留策略进行选择操作。接着,交叉操作和变异操作个体的自适应概率。最后,持续迭代遗传操作,当适应度函数不再变化或到达最大迭代次数时结束迭代。研究以非冗杂性、健全性、完备性作为恒量标准,结合农产品配送路径模型的特点确定整数编码作为编码方式。
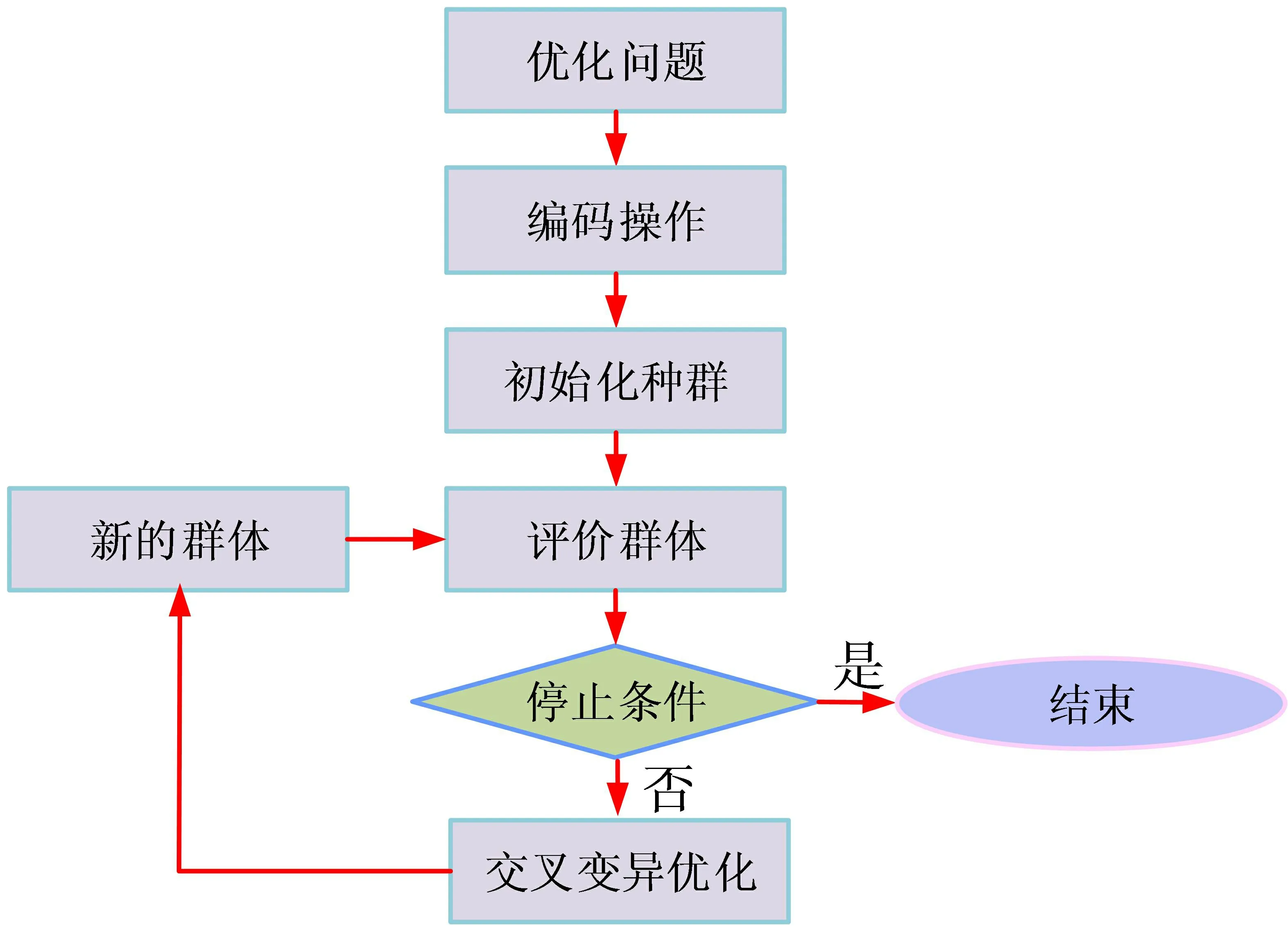
图3 改进遗传算法的示意图
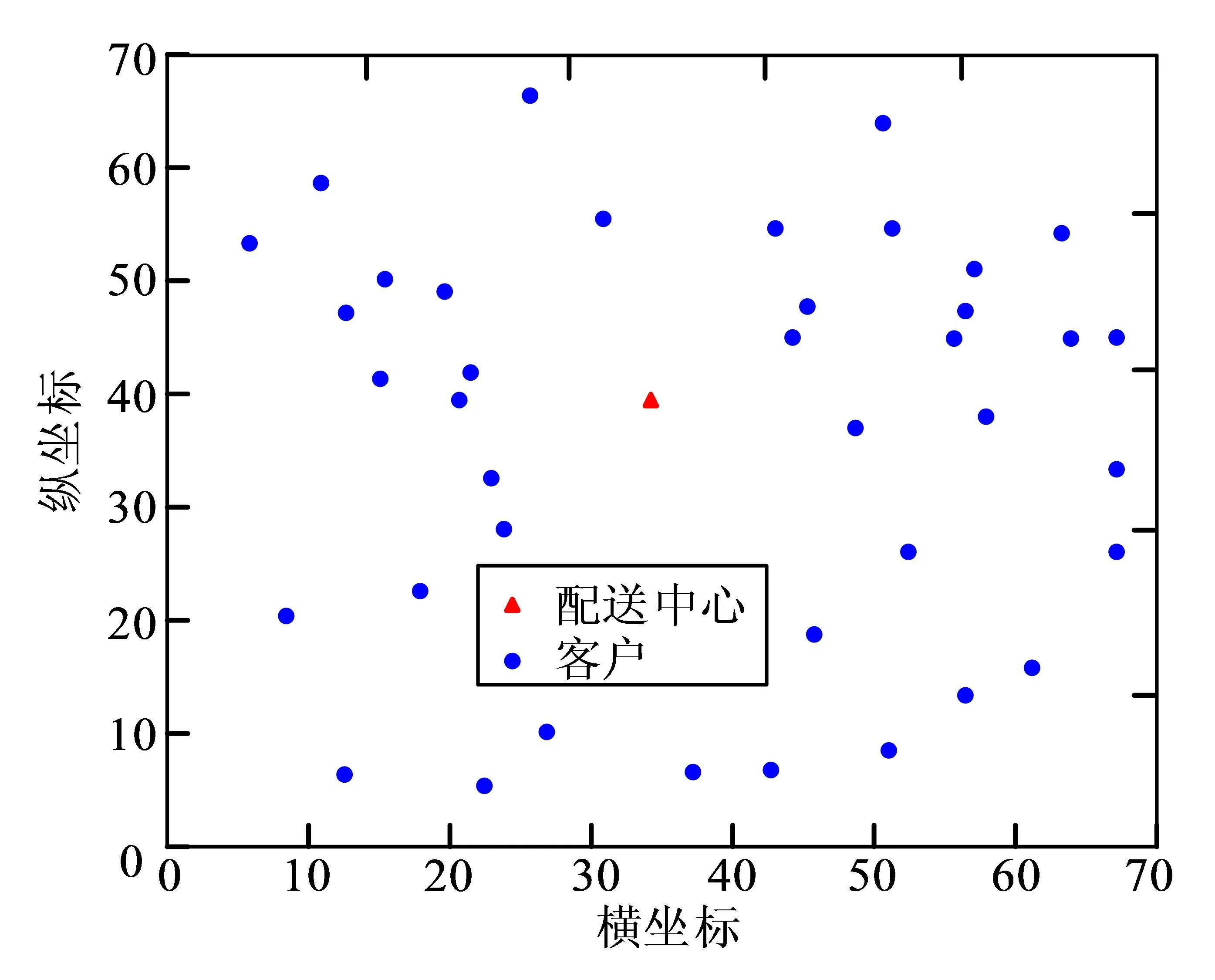
图4 配送中心及客户需求点位置图
在种群初始化方面,研究在分析客户优先顺序的基础上构建初始种群。式(3)是指客户优先关系的确定公式,即评价函数E(i)。
(3)
式(3)中,权重系数为ω1,ω2,ω3,t0i和coi分别是指配送中心与客户点i的时间和距离。对于适应度的计算,研究将目标函数的倒数作为模型的适应度函数。研究为了克服农产品物流配送模型中的问题,以及保留种群中优秀个体并变异获得更优秀的个体,对交叉和变异概率两个参数进行优化。遗传算法中,交叉概率pc的变化公式为式(4)。
(4)
式(4)中,k1和k2均为取值范围在(0,1)中的改变系数,等待交叉两个个体适应度值中较高的适应度值为f′,favg是指每代种群的平均适应度。变异概率pm的计算公式为式(5)。
(5)
式(5)中,k3和k4均为取值范围在(0,1)中的改变系数,f是指等待变异的个体适应度。联合式(4)和式(5)可知,当群体的最大适应度和个体的适应度相同时,交叉和变异概率均为0。这种调节方式在进化的末期具有一定的适用性,但在进化前期很容易陷入局部最优解。基于自适应调节方式的缺点,研究提出了改进的遗传算法。常见的选择策略为轮盘赌选择、随机竞争选择等。研究选取最为经典的轮盘赌法[9-12]。研究使用部分匹配交叉,克服一点交叉信息小而带来的较大偏差,以及多点交叉和一致交叉计算工作量的问题。对于变异算子而言,其通常和交叉操作联合应用,研究使用倒位变异。
2 改进遗传算法在农产品物流配送模型求解中的应用效果
研究采用部分Solomon算例作为数据来源分析农产品物流配送模型求解结果。该算例包括C型、R型、RC型三部分数据集,不同数据集的区别点为客户的坐标和时间窗不同。研究利用R101数据库中的50条数据,某地有一个大型农产品配送中心,周围有49个地理坐标,且每个位置对农产品的到达时间有着不同需求,如图4所示。设置运输车辆的单位启用成本为60元/(km.辆),每辆车的单位距离成本为8元/(km.辆),配送中心的配送车辆为10辆。
表1是指遗传算法和改进遗传算法在农产品物流配送模型中的求解结果。在农产品物流配送模型求解过程中,遗传算法和改进遗传算法的最优解分别为16087.9元和15129.6元,最优配送路径分别有9条和10条。
图5是指遗传算法改进前后的迭代图。遗传算法和改进遗传算法达到最优解的迭代次数分别为377代和321代。改进遗传算法的最优适应度值随着迭代次数的增加而逐渐降低,迭代过程中不断出现稳定的适应度值,出现的迭代次数分别是68次,101次,151次,321次,相应的适应度值分别为18725.6,17021.5,16583.7,15129.6。而遗传算法在迭代次数从300次开始,迭代曲线呈现急剧下降趋势。
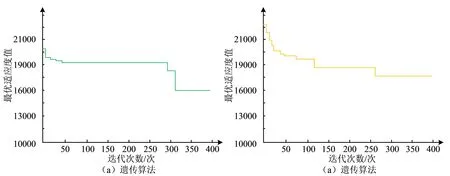
图5 遗传算法改进前后的迭代图
为了验证结合改进遗传算法的农产品物流配送效果,研究设置对比算法进行分析。通过6个数据集进行仿真分析,结果如图6所示。从图中可知,四种智能启发式算法均经过300次迭代后达到收敛,相比较于其他启发式算法而言,改进遗传算法的最优目标函数值为最具有优势。在R101,R103,C101,C103,RC101,RC103六种实例中,改进遗传算法的最低目标成本值为15129.6元,12758.3元,15426.3元,12654.3元,14895.5元,12654.8元。与传统遗传算法相比,改进遗传算法具有一定的有效性和合理性,并表现出一定的优化效果。
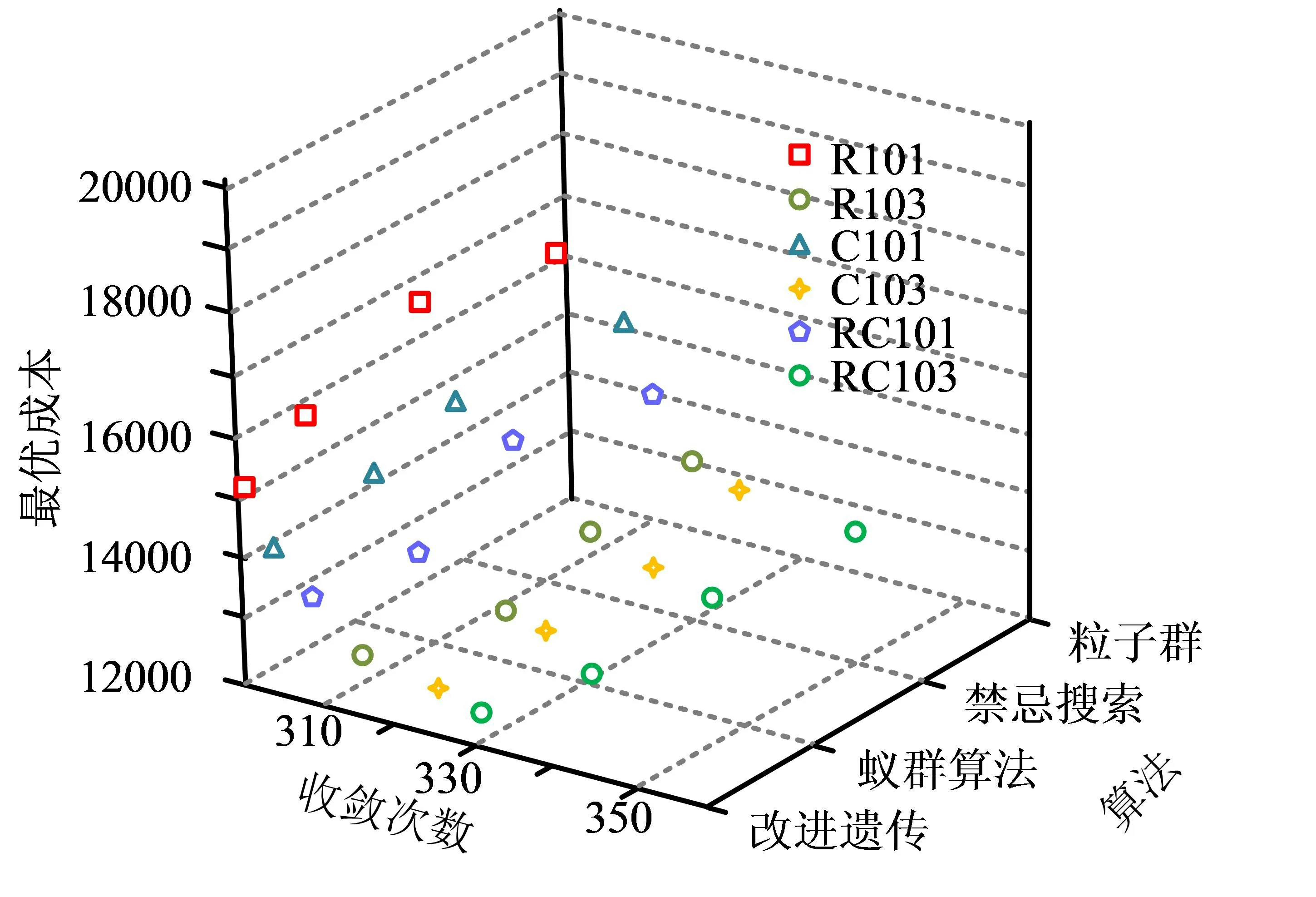
图6 不同启发式算法的农产品物流配送效果
3 结 论
针对农产品物流配送过程中多目标优化问题,研究利用改进遗传算法对农产品物流配送模型进行求解。实验结果表明,在R101,R103,C101,C103,RC101,RC103六种实例中,改进遗传算法的最低目标成本值为15129.6元、12758.3元,15426.3元,12654.3元,14895.5元,12654.8元。该模型求解方式为农产品物流配送路径优化问题的解决提供新的研究方向,可应用于新鲜农产品的运输环节。但受限于研究时间,研究在对遗传算法进行优化过程未考虑算法的复杂程度对运算效率的影响。
参考文献:;
[1] 魏庆豪,吴宪. 基于客户满意度的农产品冷链物流配送路径优化研究[J]. 湖北农业科学,2020,59(24):189-194.
[2] 宋志兰,黄益,孔民警,等. 基于TOPSIS和GRA的生鲜农产品物流配送中心选址研究 —以某地生鲜农产品配送中心选址为例[J]. 物流技术,2019,38(12):49-53+102.
[3] 夏文汇,张霞,夏乾尹. 城市生鲜农产品电商冷链物流配送模式及协同机制[J]. 江苏农业科学,2019,47(4):321-325.
[4] 丁秋雷,胡祥培,姜洋,等. 考虑新鲜度的农产品冷链物流配送受扰恢复模型[J]. 系统工程理论与实践,2021,41(3):667-677.

