面向公路施工成本模型的优化PSO算法研究①
张振生
(中铁十八局集团第四工程有限公司,天津 300350)
0 引 言
随着国家市场经济的发展,公路交通建设被纳入国家战略建设部署规划中。乡村建设与城市建设都离不开公路交通设施的完善[1]。构建成本指标体系之后,研究分析了公路施工工序和管理流程,将指标划分为四类成本,并利用PSO算法对多目标优化问题进行求解。在学者蔡彬清等人的研究中,ANP-决策在高速公路建设中具备实用性,表明基于资料调查的指标构建为成本优化提供指导[2]。同时,学者滑楠等人在机动通信保障问题利用梯度下降和PSO算法解决了机动通信保障任务分配效率低下的问题[3]。通过对国内公路建设施工成本优化前沿方法和PSO算法多领域应用的分析学习,研究提出了PSO公路成本优化模型。不仅在模型构建中确定了成本优化的目标函数,同时优化通过惯性权重的引入改进了粒子群的求解。研究旨在减低国内公路建设工程资源消耗,同时也提高施工建设企业的竞争力。
1 基于PSO算法的公路工程成本优化方法
1.1 公路工程成本计算目标模型构建
计算公路施工成本的作用体现在工程项目计划、施工准备中的资源调度、施工过程中的质量保障[4]。在整个公路施工项目前后期阶段的优化调度、责任分配中均具备重要影响。相较于传统的约束处理算法,新型的启发式算法如仿生智能群体算法更加适应大规模的数据处理和非线性的多目标问题[5]。因此,研究通过公路施工成本模型得出优化的成本函数,最后通过改进的粒子群算法(Particle Swarm Optimization,PSO)对成本目标函数进行求解。公路工程施工成本计算指标如图1所示。
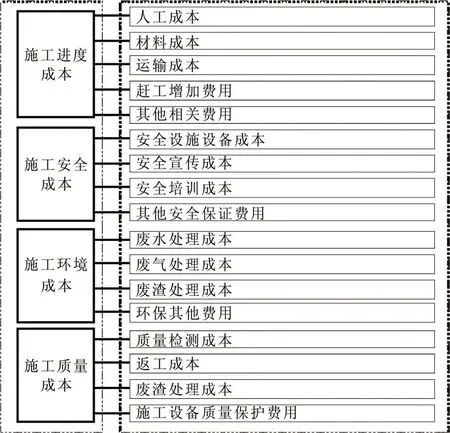
图1 公路工程施工成本计算指标
根据图1中的成本指标分别从施工进度、施工质量、施工环境、施工安全四个方面分别构建最优成本目标函数。首先施工进度的成本优化目标函数如式(1)所示。
(1)
式(1)中,优化的P1进度成本由直接成本、间接成本、以及完工的奖惩成本组成。设定施工阶段中的工序总数为N,pin为公路施工中工序i完成之后的实际支出成本。在公路施工中,工期越短完成工序的成本越高,同时工期也不能无限拉长,在到达成本最小值之后,工期时间的长度增加也伴随着成本的增加。因此,研究通过参数ρi表示工期与成本之间的递增系数。ti和tin分别为工序i的实际完成时间与正常计划完成时间。在施工进度成本计算中,人工费用等间接成本随着工期的增加而增加,因此设定参数σ表示时间与间接成本的线性关系[7]。最后,实际施工日期与施工项目合同不符时,根据合同是甲方将对于施工方进行奖励和罚款,因此将奖惩系数设定为ω,而T和Tc分别表示实际工期和合同工期。其次,施工安全成本优化模型如式(2)所示。
(2)
式(2)中,P2表示优化安全成本,pi表示公路施工工序中的安全成本,Si则表示工序中的安全系数。K1及K2表示安全成本的成长因子。由于安全成本主要由保障安全系数的支出和事故损失支出,两者成反比关系。与安全成本同理,公路施工的成本由维护环保系数支出和处理污染的成本,两者成反比[8]。其计算模型如式(3)所示。
P3min=pi×
(3)
式(3)中,P3表示优化环境成本,pi表示公路施工工序中的环境成本,ei表示工程中的环境系数,而λ1和λ2表示维护环境成本所占比例和处理污染成本所占比例。K3及K4表示环境成本的成长因子。最后,质量成本同样由维护质量水平支出成本和质量不足引发事故成本,其计算模型如式(4)所示。
(4)
式(4)中,P4表示优化质量成本,pi表示公路施工工序中的质量成本,qi表示工程中的质量系数,K5及K6表示质量成本的成长因子。最后,公路施工的整体成本优化模型如式(5)所示。
Pmin=P1min+P2min+P3min+P4min
(5)
1.2 基于粒子群算法的模型公路工程成本计算目标模型
粒子群算法作为启发式算法具备收敛计算效率高、全局搜索能力强的优点,其基本原理为通过模仿鸟群觅食行为计算个体到食物的优化距离。将鸟群中每个个体作为公路工程施工成本优化目标的可能性解,鸟群主要的影响属性为位置和速度,设定种群X由多个粒子组成,第一个粒子的位置为xi,速度为vi,个体极值为pi,群体极值为pg。因此,其速度和位置更新公式如式(6)所示。
(6)
(7)
式(7)中的惯性权重参数,为了避免算法在多目标优化中的个体极值引导偏离全局优化,设定权重参数通过线性递减的方法计算得出,其计算公式如式(8)所示。
ω=ωmax-t(ωmax-ωmin)/tmax
(8)
式(8)中,ωmax和ωmin分别表示惯性权重取值区间的上限和下限,tmax则表示最大迭代次数。最后,粒子群算法的适应度值计算公式采用Rastrigin函数计算得出,具体如式(9)所示。
(9)
从公路的进度成本、安全成本、环境成本、质量成本中可以看出,PSO算法应用于公路成本计算属于多目标优化问题。粒子群算法应用于公路成本优化模型的流程如图2所示。
从图2可以得知,粒子群的全局优化表示鸟群在空间内搜索迭代过程内的最优觅食位置,局部优化表示鸟群个体在搜索空间、迭代过程内的最优位置。在公路施工成本计算模型中,研究分别在进度成本、安全成本、环境成本、质量成本中引入奖惩因子、成长因子,安全、质量、环保等评价系数,将公路施工计算指标完全涵盖。同时在PSO算法中引入惯性权重,增加全局优化和局部优化的平衡。
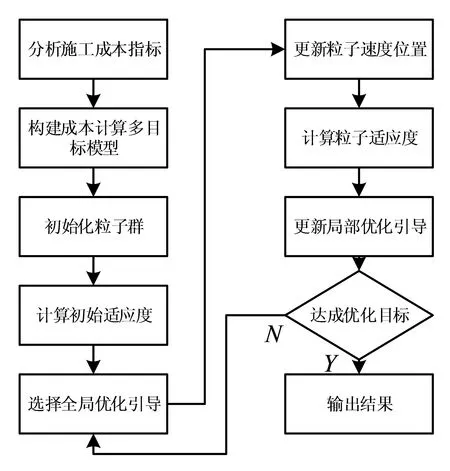
图2 粒子群算法应用于公路成本优化模型的流程
2 基于PSO智能算法的参数仿真实验及模型应用性能验证
为了验证粒子群智能算法应用于公路施工成本时的搜索性能,研究设定Rastrigin函数为适应度计算函数,将粒子群的种群数量设定为40,将学习因子设定为1.49,最大迭代次数为200次,通过MATLAB编程软件比较粒子群算法和遗传算法的迭代适应度结果,具体如图3所示。
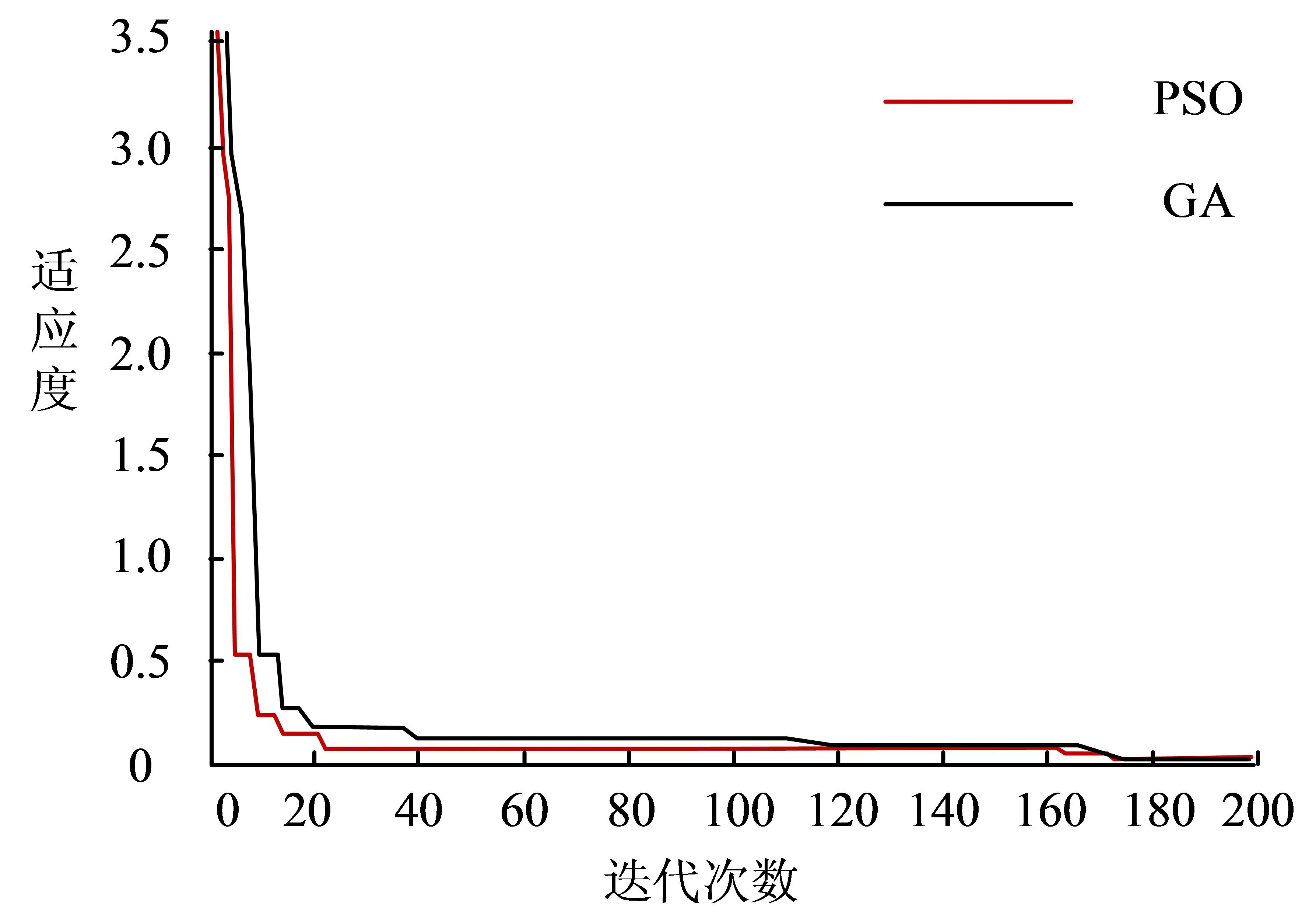
图3 粒子群算法和遗传算法的迭代过程适应度结果
由图3可以看出,在适应度比较中,PSO算法的适应度值整体小于遗传算法。实验表明,PSO算法在整体的搜索性能和迭代计算效率上优于传统的GA算法。为了平衡算法的全局搜索性能和局部优化性能,设定迭代次数为100次,目标适应度值为0.1,粒子群的种群数量设定为40,将学习因子设定为1.49,比较不同惯性权重取值情况下的算法搜索性能,具体见图4。
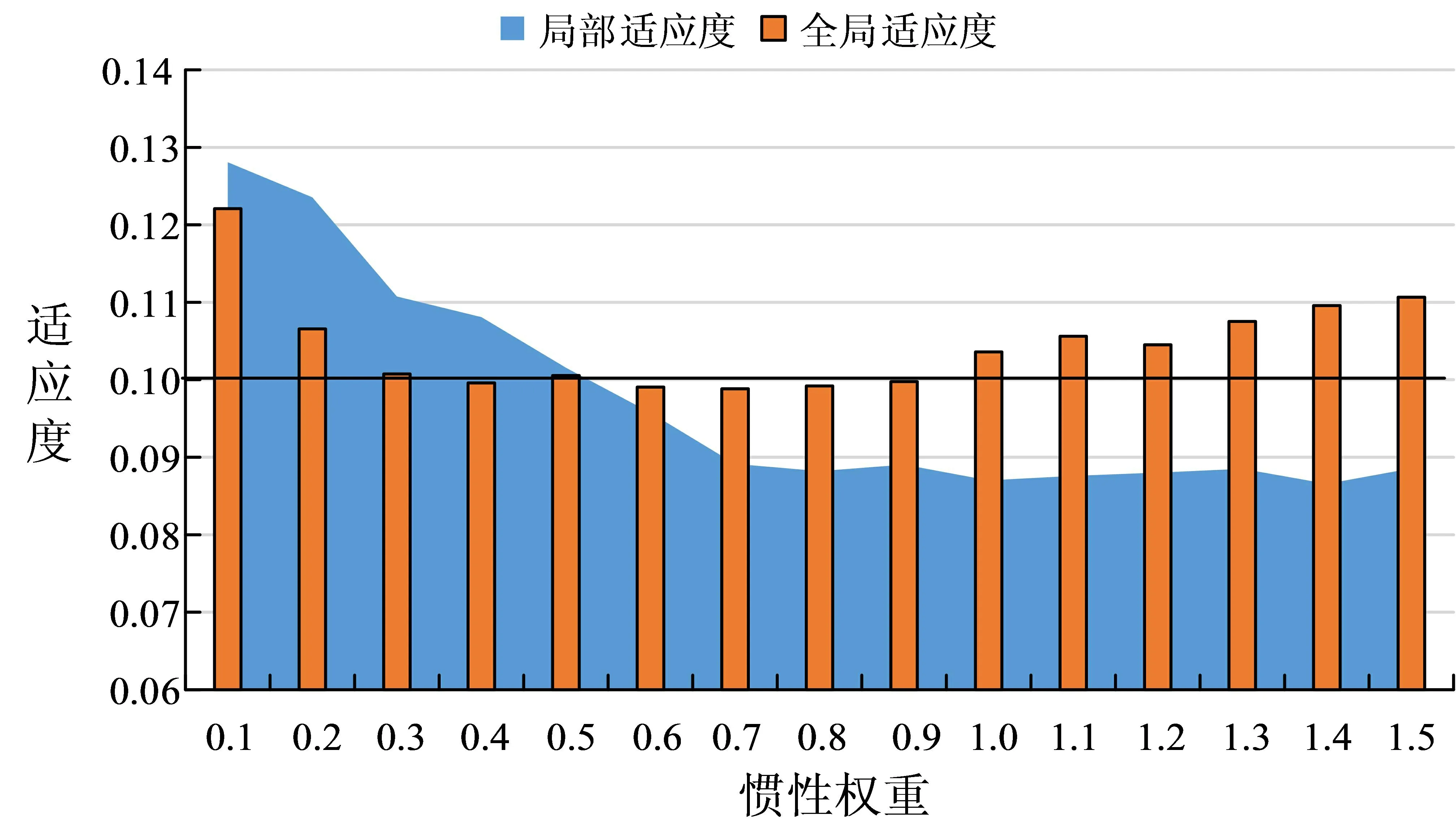
图4 不同惯性权重取值情况下的算法适应度比较
图4中,将粒子群算法的全局搜素目标适应度函数设定为0.1,可以看出当惯性权重取值为0.6,0.7,0.8,0.9时,算法的优化性能满足要求。实验以某市二级公路修建项目为实验对象,将该工程项目的45km里程的施工划分为施工准备、路基土石方开挖等十个工序。该工程的合同工期为515d,环保系数水平按照国家基本政策进行取值,区间为0.78-1.0;同时根据工程性质和实际情况将质量系数的取值区间设定为0.85-1.0,安全系数取值区间为0.9-1.0。具体样本案例的工程参数如表1所示。
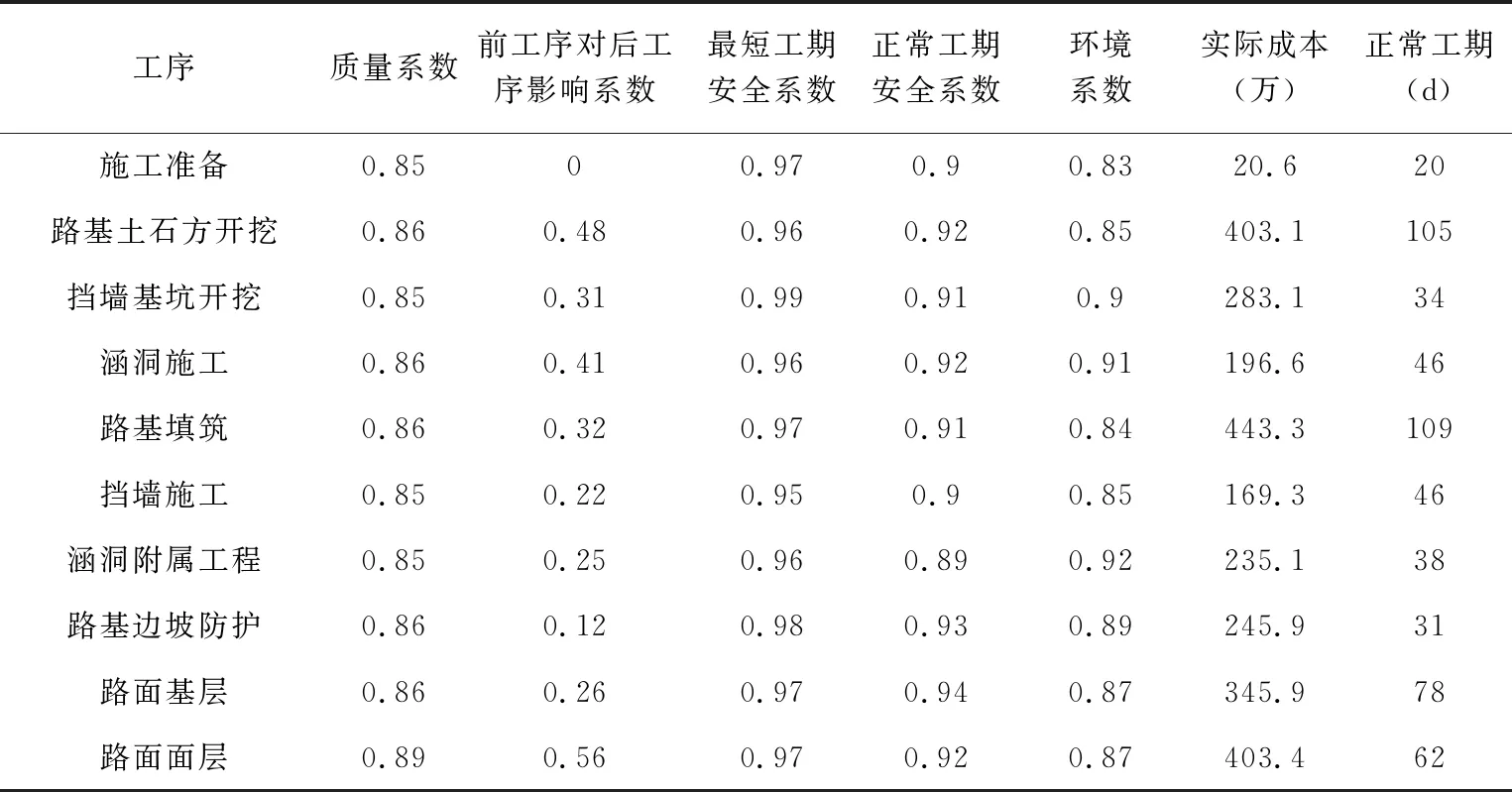
表1 工程样本参数
除上表1中具体参数以外,研究根据施工具体情况将施工进度成本中的奖惩因子设定为3万/d,将表示时间与间接成本线性关系参数σ设定为0.4。设定安全成本的成长因子K1,K2取值为1.7和6.5,环境成本成长因子K3,K4取值为2.8和2.5,最后将质量成本成长因子K5,K6设定为5,1.2。在实例分析中,构建的粒子群公路成本优化算法在种群数量上取值500,并设定最大迭代次数为500次,其余参数与仿真实验相同。将实验分析结果数据整理为图5。
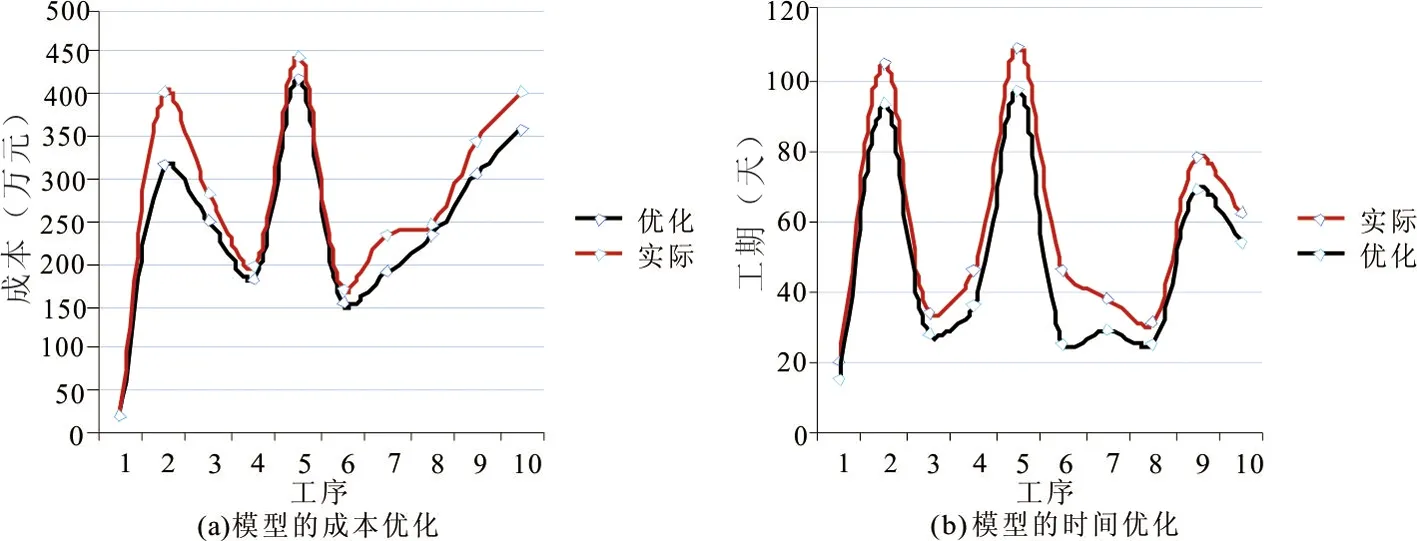
图5 公路成本优化模型性能结果分析
图5(a)中,在施工的所有工序中,路基土石方开挖的成本优化成果最佳,从目标的403.1万减少到了317.1万,在施工成本中,目标整体成本总计为2746.3万,而PSO算法模型优化之后成本为2430.2万,成本减少了316.1万。在图(b)中,施工工序中工期优化减少最多的为挡墙施工,从计划的46d减少到了模型计算结果的25d,公路施工整体的工期从569d减少到了471d,满足了合同工期的515d要求。实验表明,研究构建的PSO公路施工成本优化模型不仅可以有效缩减施工成本,同时可以将施工的耗时减少。
3 结 语
施工质量、进度、安全、环境保护等因素都会对公路建设工程的成本造成直接影响。故研究构建了PSO公路成本优化模型,用于减少施工项目中的成本和资源消耗。通过对比PSO算法和GA算法迭代适应度的仿真实验,本次研究确定了改进粒子群在计算效率和适应度结果中性能更佳。同时实验通过对比全局适应度和局部适应度确定了惯性权重的取值区间为0.6-0.9。在45KM的公路施工项目实例分析中,研究提出的成本优化模型的实用性能得以保证。实验数据表明,PSO算法模型优化将施工成本从2746.3万降低到了2430.2万,减少了316.1万;而在施工工期优化中,路施工整体的工期从569d减少到了471d,缩短了98d。实验表明,研究构建的PSO公路施工成本优化模型不仅可以有效缩减施工成本,同时可以将施工的耗时减少。

