均布荷载作用下简支梁临界荷载的一种优化设计①
尤 超, 梁冠军, 沈晨姝, 余 龙
(1.滁州职业技术学院,安徽滁州 239000; 2.同济大学土木工程学院,上海 200092;3.中国能源建设集团安徽省电力设计院有限公司,安徽合肥230009)
0 引 言
在建筑结构设计中,简支梁是设计中最常见的一种结构形式,它常常受到各种荷载的作用,结构上的任何一处都可能产生较大应力与变形[1-4],从而使简支梁的结构发生变形破坏。以简支梁受均布荷载变形后的平衡状态为研究对象,建立受力模型,并对结构进行受力分析,最终确定简支梁的优化设计求解变形和转角[5-8],并把结果与有限元分析结果进行比较,进而验证优化算法的正确性[9-10]。
1 均布荷载作用下建立简支梁结构的受力模型
假设在均布荷载q作用下,简支梁横截面为矩形,宽b,高q,跨度为l,弯曲刚度EI,在受力前后变形如图1所示。

(1)简支梁变形前,由静力平衡求得各约束为:
(1)
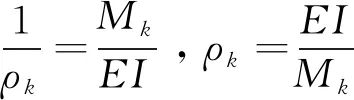
(2)
(3)各微段在坐标系下的递推关系式:
在坐标系XAY下,第k个微段的左端点为Sk-1(Xk-1,Yk-1),右端点为Sk(Xk,Yk),以变形曲线Sk-1(Xk-1,Yk-1)点的切线和法线建立坐标系xkSk-1yk,则第k微段的转角与变形为Δθk,Δxk,Δyk,由式(3)计算:
(3)
式(3)中第k个子段曲率中心Ck点坐标如式(4):
(4)
2 计算结构优化与目标函数
(5)
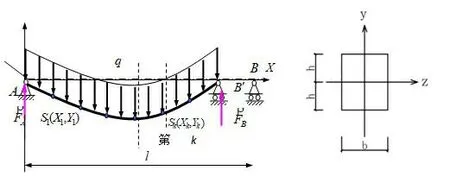
图1 简支梁受力变形后平衡状态图

图2 简支梁第k子段内力变形关系分析图
3 算例分析
用上述计算优化算法均布荷载作用下简支梁的变形及转角和采用有限元分析软件的计算结果如表1,并进行对比。

表1 均布荷载q大小不同时简支梁的挠度和转角
选取均布载荷q=50作用时的情况分析,采用本文提出的优化算法计算简支梁转角和各分点的挠度,将计算各分点的转角和坐标结果如表2,以及用有限元软件分析计算的各分点的转角和坐标结果如表3。
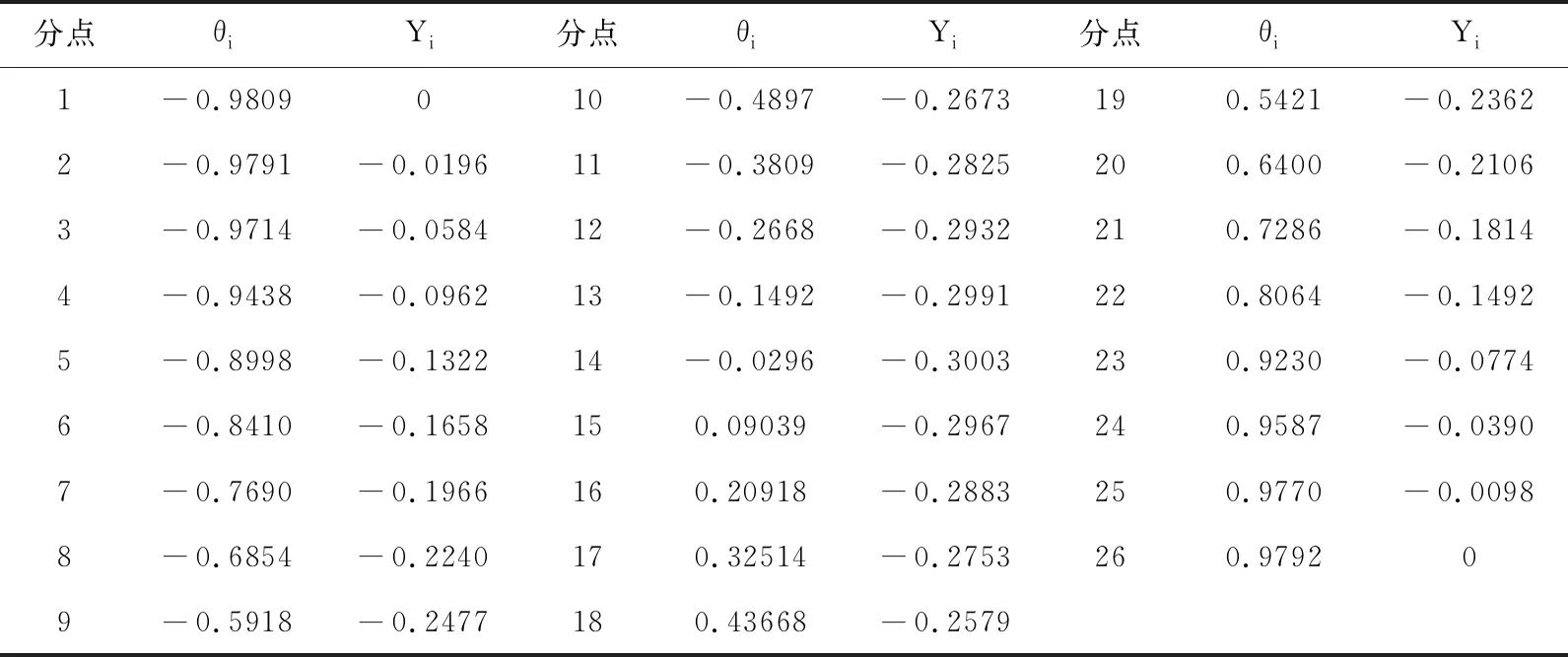
表3 采用有限元分析软件计算Yi时梁上各分点变形和转角
根据表2和表3的计算结果,绘制在均布荷载q=50作用时,采用优化算法和有限元方法的变形与转角的平衡状态拟合如图3所示。
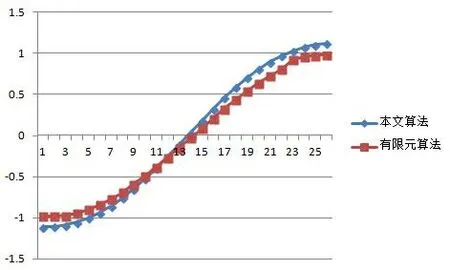
(a) 挠度曲线
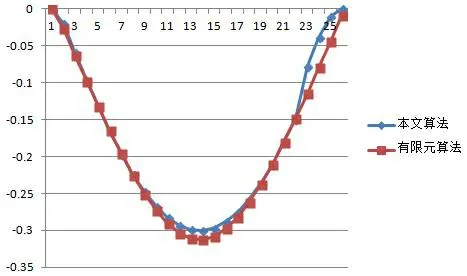
(b) 转角对比图
从图3的挠度曲线图(a)和转角对比图(b),可以看出采用上述提出的优化算法和有限元分析软件的计算结果具有很好的一致性,进而说明所研究的优化算法在解决均布荷载作用下的简支梁变形问题的有效性和正确性。
4 结 语
通过计算实例,针对简支梁结构在均布荷载作用下的计算问题进行了分析,基于微分方程的初值问题的求解原理,建立优化算法,求解未知力,编制优化求解程序,分析了计算算例,并同有限元方法的计算结果的进行对比,表明所研究的算法在求解简支梁力学问题上具有很好的有效性,从而为处理工程结构问题,提供了一种求解的新思路。

