基于二元蚁群算法的高碳制造业碳排放多目标规划方法

施志晖,王景斌,黄 进

(1.江苏苏宁银行股份有限公司,江苏 南京 210019;2.南京大学 工程管理学院,江苏 南京 210093)

为了满足城镇化快速发展,以高碳制造业为主的能源消费行业增长态势迅猛,满足了人们日益增长的刚性需求的同时,也造成了碳排放越来越严重[1]。从整体碳排放数据来看,高碳制造业产生的碳排放总量,占了工业总体碳的一半以上[2]。尤其是金属加工业、石油冶炼、化学原料制备等行业,加工过程中产生的碳排放量是其他行业碳排放总数的3倍左右。因此,想要实现碳排放总量降低,必须完成高碳制造业碳排放控制。保证企业生产效益的同时,进行碳减排目标设置,成为当前高碳制造业转型升级的关键点。目前,关于高碳制造业碳排放问题,研究人员已经开展了大量工作,但研究结果差强人意。

文献[3]依托于中央发布的双碳战略,提出以国土空间规划为核心的差异化控碳模式。在低碳要求下,根据区域差异化控碳要求,建立不同区域的碳排放控制方案,再结合国土空间总体规划模式,合理衔接各个阶段的控碳思路,形成最终低碳规划框架。但是,该方法减排效果较差。文献[4]深入分析了碳预算与碳中和的联系,在碳中和背景下,根据企业碳循环要求,建立碳排放规划目标和约束条件。并与其他规划方法进行比较,建立完善的未来能源规划体系。但是,该方法成本较高。文献[5]以能源回弹效应为基础,设计符合碳减排要求的突变技术门槛。结合Hansen门限面板和CD生产函数,建立能源回弹模型,保证高碳制造业经济效益的同时,实现碳排放量降低。但是,该方法实施耗时较长。

文中参考上述规划方法,提出一种新的碳排放多目标规划方法,并融合二元蚁群算法,避免多目标规划求解的局部最优化问题,生成高碳制造业碳排放最优规划方案。

1 基于二元蚁群算法的高碳制造业碳排放多目标规划方法设计

1.1 提取企业碳排放驱动因素

高碳制造业碳排放的规划,需要从碳排放驱动因素入手,文中提出采用全局空间自相关方法,描述企业碳排放空间特征[6]。本文利用Moran’s I指数,建立全局空间自相关分析模型:

(1)

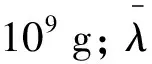
之后,再运用空间邻接方式,依据空间权重探究局部空间地区异常值,弥补全局空间自相关分析结果的不足之处,局部空间自相关分析模型为

(2)

(3)

式中:M为局部Moran’s I指数。当式(2)计算结果高于0,表明当前碳排放空间聚集特点为高-高、低-低。反之,高碳制造业的碳排放空间聚集特点为高-低和低-高。

依据高碳制造业的碳排放特点,文中采用静态空间面板模型,分析当年碳排放变化趋势[7],再考虑滞后一期的影响,建立如下所示的动态空间面板模型:

(4)

式中:u为年份;D为碳排放量,109g;Dau-1为滞后一期的碳排放;τ1、τ2为空间滞后系数;R为碳排放影响因素;θ0、θ1、θ2为待估系数;ψ为地区固定效应;ϑ为随机扰动项。

1.2 建立多目标碳排放规划模型

文中提出的碳排放规划方法,将多目标规划数学模型表示为

(5)

式中:f(·)为目标函数;x为决策变量;n为变量数量;g(x)、l(x)为目标函数约束条件。

根据式(5)可知,多目标碳排放规划模型主要包括三个要素,分别是决策变量、目标函数以及约束条件[8]。将高碳制造业产业结构,融合到多目标碳排放规划模型建设过程中,形成图1所示的高碳制造业产业结构演化机制,达到经济可视化发展的目的。

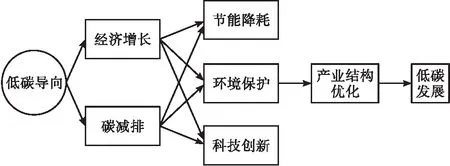
图1 低碳导向下高碳制造业产业结构演变机制

从图1可以看出,高碳制造业碳排放多目标规划,主要包括经济增长和碳减排两方面,前者需要达到最大化,后者则是要达到最小化,在二者平衡状态下,推动高碳制造业产业结构升级[9]。

高碳制造业的结构优化,是推动经济增长的基础。本文建立多目标碳排放规划模型,需要将经济发展规模,作为第一个规划目标。考虑到经济产出数据的复杂性,文中选用产业增加值为指标,建立最大化优化目标函数:

(6)

式中:max为最大值;v为高碳制造企业产出;e为高碳制造企业产业增加值系数。

此外,为了达到碳减排效果,需要在保证企业经济发展规模的同时,建立最小化碳排放目标函数:

(7)

式中:min为最小值;j为高碳制造企业碳排放系数。按照上述设计,完成高碳制造业碳排放多目标规划模型的初步建立,之后还需要进行规划模型约束条件设置。

1.3 设置多目标规划约束条件

根据高碳制造业工作模式,文中提出从碳排放、能量消耗、投入产出、科技投入以及产业扩张等五个方面,分别设置规划约束条件。具体的约束条件表达公式如下所示:

(8)

上述多目标规划约束条件中,投入产出均衡约束直接反映了高碳制造业的内部结构联系,也是碳排放规划的基础内容。而碳排放约束条件,表示了规划模型的边界,也是碳排放规划的现实意义。而其他三个约束条件,是辅助碳排放规划的重要条件。至此,完成整个碳排放规划模型的设计。

1.4 设计二元蚁群规划求解算法

针对上述建立的多目标规划模型,文中提出以二元蚁群原理为基础的规划求解算法,根据蚂蚁信息素交换结果,获取最佳碳排放规划方案[10]。二元蚁群算法运行过程中,将蚂蚁放置于初始位置,让其进行自动爬行,蚂蚁爬行的二元网络图如图2所示。

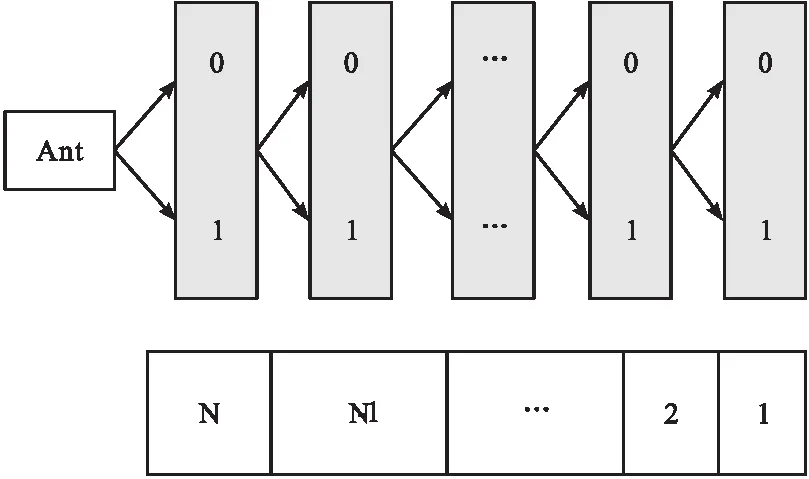
图2 蚂蚁爬行的二元网络图

在二元蚁群爬行过程中,根据每个碳排放规划路径的信息量,确定蚂蚁移动方向,蚁群移动概率计算公式为

(9)

式中:φ为蚂蚁;ξ为蚂蚁移动概率;i,o为蚂蚁位置;(0)、(1)为蚂蚁转移方向;δ为蚂蚁移动轨迹能见度;γ为移动轨迹残留信息量;J为轨迹的相对重要性;H为能见度的相对重要性。

此外,蚁群运动过程中,最优个体的信息素更新模式,如下所示:

(10)

式中:φ为轨迹持久度;ε为迭代次数。

上述二元蚁群规划求解算法主要应用二进制编码技术。考虑到高碳制造业碳排放多目标规划求解中,包含数量庞大的非支配解,极易引发局部最优化问题。文中为了解决这一问题,加强“全局探索”和“局部优化”之间的平衡性,加入多个环境评价指标,实时反映蚁群求解环境,同时表达了算法收敛性。

文中所应用的环境评价指标,包括肥沃程度、生长程度以及平均分布距离三项内容,分别表示当前非支配解数量、新非支配解数量以及非支配解的聚集密度。其中,平均分布距离表达公式为

(11)

式中:T为平均分布距离,m;ν为选定区域;B为非支配解的个数,个;A为子目标的个数,个;G为区域中心种子。

基于式(11)得出的平均分布距离,对蚁群搜索环境进行评价,以此来延长该区域搜索次数,将其标注为奖励搜索次数。根据所有奖励搜索次数,计算区域环境奖励:

(12)

式中:C为区域环境奖励;∂为奖励搜索次数;ιh为奖励程度;W为碳排放多目标规划方案总数量。

通过上述计算模式,实时调整奖励搜索次数,实现碳排放多目标规划收敛性的提升。简单来说,当蚁群搜索过程中,停留在周边环境较好的区域,需要将该区域环境因素作为参照,对全局环境因素进行处理,加强全局搜索效率。同样,这个具有较好环境条件的区域,也包含更多的环境奖励,可以得到更加彻底的开发。

综上所述,运用二元蚁群规划求解算法,汇总蚁群运动目标点,生成最优碳排放多目标规划方案。

2 实证分析

为了满足城市工业化发展要求,近年来高碳制造业发展态势不断加快,能源消费量也随之增长,打破了其自身产业结构的发展规律。能源消耗引发了高碳制造业碳排放量的提升,造成严重的环境污染,为了解决这一问题,未来一段时间内节能减排会成为主要研究方向。文中针对高碳制造业企业,提出融合了二元蚁群算法的,碳排放多目标规划方法。为了验证文中提出方法的有效性,特进行实证分析。

2.1 变量设定

本次实证分析以辽宁省为例,采用空间自相关分析方法,分析该省份高碳制造业碳排放空间集聚特点,得出图3所示的碳排放Moran散点图。

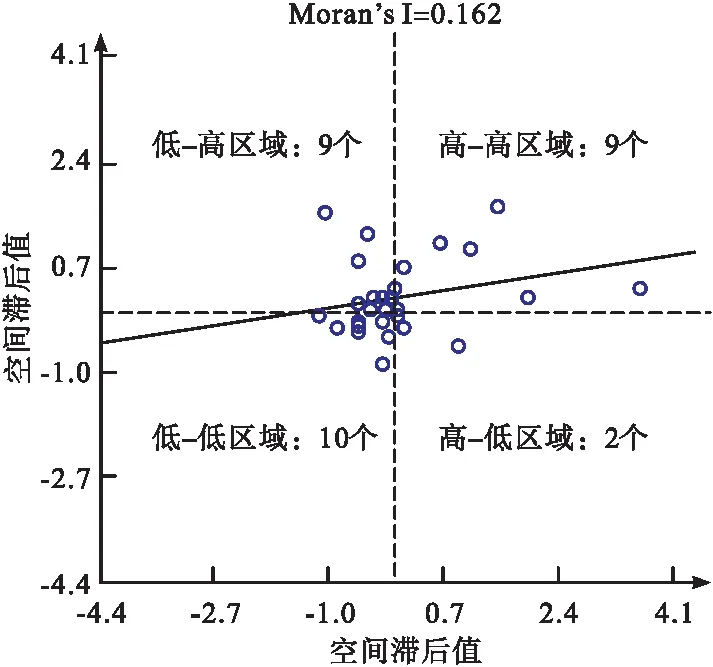
图3 高碳制造业碳排放Moran散点图

根据图3可知,该研究区域高碳制造业,碳排放Moran’s I值达到了0.162,反映了该区域碳排放总体呈现出空间自相关特点。其中,具有低-高、高-高分布特点的碳排放聚集区域均为9个,具有低-低分布特点的碳排放聚集区域为10个,而高-低区域仅有2个,这种特点表明该省域高碳制造业碳排放,存在不断加深的空间溢出效应。

本次分析过程中,从研究区域内选取24个典型高碳制造业,作为碳排放多目标规划的模型变量,具体的设定情况如表1所示。

表1 模型变量设定表

运用表1所示的模型变量,进行碳排放多目标规划研究。

2.2 数据来源与处理

本次实证分析所采用的数据,均来自官方网站,从《能源统计年鉴》《温室气体清单指南》等多个文档中,选取适用于本次实证分析的数据,整合形成实证数据集。根据IPCC提供的数据信息,提取不同能源相对应的碳排放因子,结合实证数据集中显示的高碳制造业能源消费量,得出每个高碳制造企业的具体碳排放量,具体计算公式为

(13)

式中:σ为碳排放总量,109g;W为燃料消费量,t;α为热值转换系数;β为碳排放系数。

除此之外,还可以通过企业产出和增加值,得出高碳制造业增加值系数。利用企业碳排放量数据和总产出数据,得出碳排放系数。在产值规模约束的角度进行分析,针对高碳制造业的当年增加值,计算其占据总工业增加值的比例,增加15%得到产值规模上限,减少15%则可以得到产值规模下限。需要注意的是,高碳制造业目前发展趋势良好,短时间内不可能出现某一行业直接破灭的现象,所以在设置产值规模下限时,需要保证其高于1%。

2.3 碳排放规划结果分析

以上述数据为基础,运用文中提出的碳排放多目标规划方法,对高碳制造业碳排放进行改进,与规划前企业碳排放量进行对比,得到图4所示的碳排放量统计结果。

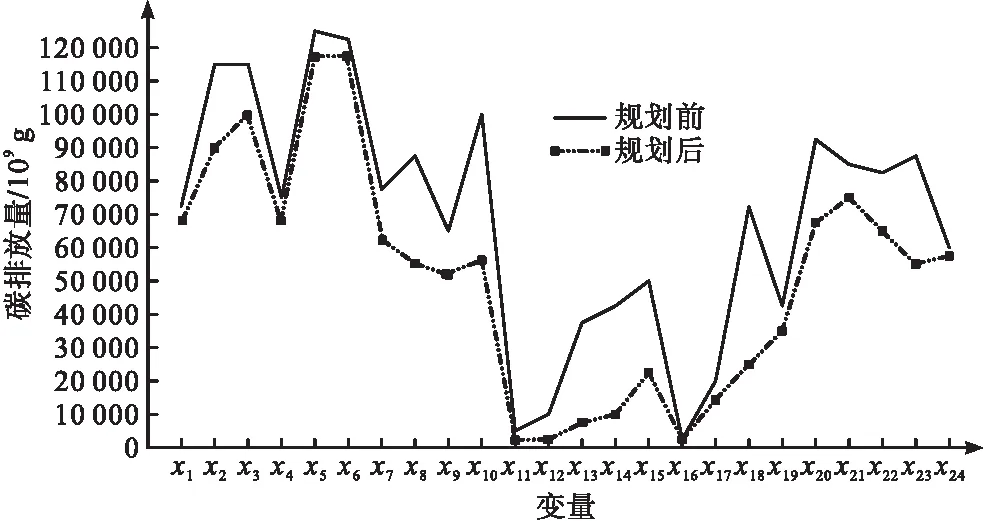
图4 规划后高碳制造业碳排放量统计图

根据图4可知,文中提出的方法应用后,对高碳制造业碳排放量进行良好规划,使得碳排放量相比规划前有了明显降低。从整体来看,文中设计的规划方法应用后,使得高碳制造业碳排放量总量减少了128 979×109g,使得高碳制造业碳排放量降低了12.35%,有助于高碳制造业向着绿色可持续发展方法进步。

3 结 语

文中以降低高碳制造业碳排放为主要目标,提出融合了二元蚁群算法的多目标规划方法,考虑了企业产业增加值的同时,达到碳排放最小化。同时,针对能源消耗、碳排放等方面设置相应的约束条件,再运用二元蚁群算法,求解出最优规划方案。从实证分析来看,文中提出方法的应用,使得碳排放量总量减少了12.35%,表明了该方法的良好应用效果。

但是,由于研究时间尚浅,文中提出的规划方法依旧存在不足之处。下一步研究过程中,可以选择更多规划指标,考虑社会效益等多种指标,生成更优的高碳制造业碳排放多目标规划方案。