测电阻方法探微

成金德

測电阻是中学物理实验中的核心内容，是历年高考实验部分的重头戏.测量电阻时，根据问题的要求需要设计测量电路、选择电表量程、选用滑动变阻器和熟练应用相关的物理规律，以测电阻为线索的实验问题可以考查学生的实验迁移能力、实验设计能力和知识应用能力.为此，弄清和掌握测量电阻的方法至关重要，下面就此问题作详尽的分析和探讨.

一、伏安法

测出被测电阻两端的电压U和通过被测电阻的电流I，根据欧姆定律I=UR可求出被测电阻的阻值R=UI.这种方法叫做伏安法.

1.常规方法

（1）电流表外接法

如图1所示是一种用伏安法测电阻的电路，叫做电流表外接法.

在电流表外接法中，由于伏特表的分流作用，使电流表的测量值大于通过被测电阻的真实值，由欧姆定律得：

R测=U测I测=URIR+IV=RVRV+Rx·Rx，所以，测量值小于真实值.

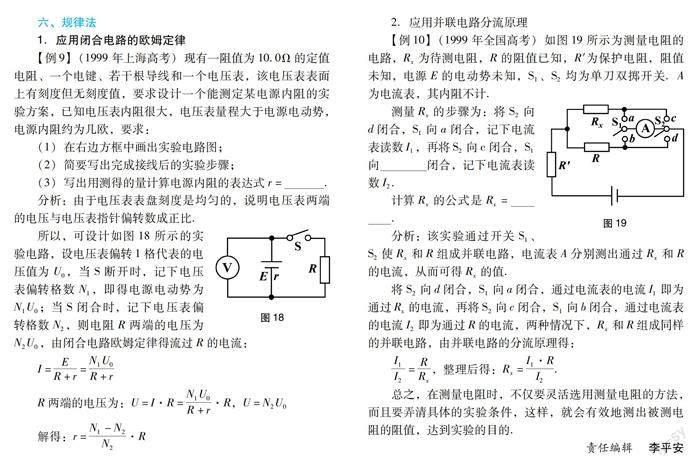
可见，用电流表外接法测量电阻时，必须满足RV》Rx的条件，即此种接法适合于测量小电阻.

（2）安培表内接法．

如图2所示是另一种用伏安法测电阻的电路，叫做电流表内接法.

在电流表内接法中，由于电流表的分压作用，使电压表的测量值大于被测电阻两端的真实电压，由欧姆定律得：

R测=U测I测=UR+UAI测=Rx+RA，所以，测量值大于真实值.

可见，用电流表内接法测量电阻时，必须满足Rx》RA的条件，

即此种接法适合于测量大电阻.

【例1】（2020·全国卷Ⅰ）某同学用伏安法测量一阻值为几十欧姆的电阻Rx，所用电压表的内阻为1 kΩ，电流表内阻为05 Ω.该同学采用两种测量方案，一种是将电压表跨接在图3所示电路的O、P两点之间，另一种是跨接在O、Q两点之间.测量得到如图4所示的两条U-I图线，其中U与I分别为电压表和电流表的示数.回答下列问题：

（1）图4中标记为Ⅱ的图线是采用电压表跨接在__________（选填“O、P”或“O、Q”）两点的方案测量得到的.

（2）根据所用实验器材

和图4可判断，由图线__________（选填“Ⅰ”或“Ⅱ”）得到的结果更接近待测电阻的真实值，结果为__________ Ω（保留1位小数）.

（3）考虑到实验中电表内阻的影响，需对（2）中得到的结果进行修正，修正后待测电阻的阻值为__________ Ω（保留1位小数）.

分析：（1）若将电压表接在O、P之间，根据欧姆定律得：I=URV+URx

即：U=RxRVRx+RV·I，由一次函数关系可知图线的斜率为：k1=RxRVRx+RV.

若将电压表接在O、Q之间，根据欧姆定律得：

Rx=U-IRAI

解得：U=I（Rx+RA）

由一次函数关系可知图线的斜率为：k2=（Rx+RA）

显然，k2>k1，从图像中看出，kⅠ>kⅡ

所以，图线Ⅱ是采用电压表跨接在O、P之间的方案得到的.

（2）因为待测电阻是阻值为几十欧姆的电阻，通过图线的斜率大致可估算出待测电阻为50 Ω左右，由于RVRx

说明更符合Rx》RA的条件，所以电压表应跨接在O、Q之间，所以选择图线I得到的结果较为准确.

（3）根据图像可知：Rx=3V-1V596 mA-20 mA≈505 Ω

考虑电流表内阻的影响，则修正后的待测电阻为：

Rx′=Rx-rA=505 Ω-05 Ω=500 Ω.

2.电表的反常规用法

已知内阻的电流表（或电压表），它们不仅可以测量电流（或电压），而且可以测量电压（或电流），也即电流表可当作电压表使用（或电压表可当作电流表使用），从而实现电表的反常规应用.

【例2】某同学在实验室测量某一阻值大约90 Ω左右的电阻，现有如下的实验器材可供选择：

A.电流表A1（量程50 mA，内阻r1=100 Ω）

B.电流表A2（量程150 mA，内阻r2大约为40 Ω）

C.电流表A3（量程3 A，内阻r3大约为01 Ω）

D.滑动变阻器R（0～20 Ω，额定电流2 A）

E.直流电源E（9 V，内阻不计）

F.导电元件Rx

G.开关一只，导线若干

为精确地测量该电阻的阻值，请选择合适的仪器，画出实验电路.

分析：考虑到实验器材中缺少电压表，但由于电流表A1的内阻已知，且电流表A1能测最大电压为：U max =50×10 -3 ×100 V=5 V，显然，可以满足利用电流表测量电压的实验要求.在测量过程中流过电阻的电流最大值为I max =U max R=5 V90 Ω=56 mA，则电流表应选用A2.为了多测量数据而减小误差，滑动变阻器需应用分压式接法，由于电流表A2的内阻未知，则选用电流表外接法，电路图如图5所示.

3.电阻箱（或定值电阻）代替电表

如果能测出电阻箱（或定值电阻）两端的电压，根据欧姆定律可求出通过电阻箱（或定值电阻）的电流，即此时可将电阻箱（或定值电阻）当作电流表使用；同理，如果能测出通过电阻箱（或定值电阻）的电流，根据欧姆定律可求出电阻箱（或定值电阻）两端的电压，即此时可将电阻箱（或定值电阻）当作电压表使用.

【例3】要测量电压表V1的内阻R V1 ，其量程为0～2 V，内阻约为2 kΩ.实验室提供的元件有：

A.电流表A，量程为0～06 A，内阻约为01 Ω；

B.电压表V2，量程为0～5 V，内阻约为5 kΩ；

C.定值电阻R1，阻值为30 Ω；

D.定值电阻R2，阻值为3 kΩ；

E.滑动变阻器R3，最大阻值为100 Ω，允许通过的最大电流为15 A；

F.电源E，电动势为6 V，内阻约为05 Ω；

G.开关S一个，导线若干.

请设计一个测量电压表V1内阻R V1 的实验电路.要求测量尽量准确，实验必须在同一电路中，且在不增减元件的条件下完成.试画出符合要求的实验电路图.

分析：由于电压表的内阻较大，流过电压表的电流很小，因此，使用电流表直接测量通过电压表V1的电流，电流表指针偏转很微弱，读数误差较大.

这样，只能让定值电阻与待测电压表V1串联起来，如果能测出定值电阻两端的电压，由欧姆定律求出通过定值电阻的电流，则通过被测电压表V1的电流就知道了.又因为电压表V1能读出自身两端的电压，这样，就可以测出电压表V1的电阻.

当电压表V1、V2同时满偏时，由于电压表V1允许通过的最大电流约为1 mA，则R 定值 =U2-U1I V1 =3 kΩ.可见，定值电阻应选用R2，又因为被测电压表内阻较大，而滑动变阻器阻值较小，则控制电路要用分压式接法.所以，实验电路如图6所示.

二、等效法

测量某电阻时，若将电阻箱替换待测电阻，如果替换前后对电路产生的效果相同，则待测电阻的阻值与电阻箱的有效电阻相等.

1.电流等效法

如图7所示的电路，闭合开关S1、S2，调节滑动变阻器的滑片P，使电流表指针指在适当的位置，记下电流表的示数I.

再断开开关S2，闭合开关S3，保持滑动变阻器的滑片P位置不变，调节电阻箱的阻值，使电流表的示数仍为I.

显然，此时电阻箱连入电路的有效阻值R0与未知电阻Rx的阻值相等，即Rx＝R0.

2.电压等效法

如图8所示的电路，闭合开关S1、S2，调节滑动变阻器的滑片P，使电压表指针指在适当的位置，记下电压表的示数U.

再断开S2，闭合S3，保持滑动变阻器的滑片P位置不变，调节电阻箱的阻值，使电压表的示数仍为U.

显然，此时电阻箱连入电路的有效阻值R0与未知电阻Rx的阻值相等，即Rx＝R0.

【例4】某同学准备把量程为0～500 μA的电流表改装成一块量程为0～20 V的电压表.他为了能够更精确地测量电流表的内阻，设计了如图9所示的实验电路，图中各元件及仪表的参数如下：

A.电流表G1（量程0～10 mA，内电阻约100 Ω）

B.电流表G2（量程0～500 μA，内电阻约200 Ω）

C.电池组E（电动势30 V，内电阻未知）

D.滑动变阻器R（0～25 Ω）

E.电阻箱R1（总阻值9 999 Ω）

F.保护电阻R2（阻值约100 Ω）

G.单刀单掷开关S1，单刀双掷开关S2

（1）实验中该同学先合上开关S1，再将开关S2与a相连，调节滑动变阻器R，当电流表G2有某一合理的示数时，记下电流表G1的示数I；

然后将开关S2与b相连，保持__________不变，调节__________，使电流表G1的示数仍为I时，读取电阻箱的读数r.

（2）由上述测量过程可知，电流表G2内阻的测量值rg＝__________.

（3）若该同学通过测量得到电流表G2的内阻为190 Ω，他必须将一个__________kΩ的电阻与电流表G2串联，才能改装为一块量程为20 V的电压表.

分析：应用等效法，只要保持滑动变阻器的滑片位置不变，调节电阻箱R1的阻值，使得电流表G1的示数仍为I时，则此时电阻箱的阻值与电流表G2内阻相等，即电流表G2内阻的测量值rg=r.

电流表G2再串联一个电阻即可改装成一个电压表，由欧姆定律得：U=Ig（rg+R）

即：R=UIg-rg=2500×10 -6  Ω-190 Ω=3810 Ω

三、半偏法

1.电流表半偏法

如图10所示的电路，断开开关S2，闭合开关S1，调节滑动变阻器R1，使电流表的示数等于电流表的量程Im；保持滑动变阻器R1的阻值不变，闭合开关S2，调节电阻箱R2，使电流表的示数等于 12Im ，若满足R1RA，则此时电阻箱R2的有效阻值约等于电流表的内阻，即 RA＝ R2.

由于在闭合开关S2时，总电路的电阻减小，导致总电流增大，虽然此时的电流表半偏，但流经R2的电流比电流表所在支路的电流大，

所以，R2的电阻实际上比电流表的电阻小，所以，这样测出的电流表的内阻偏小.

2.电压表半偏法

如图11所示的电路，先将电阻箱R2的阻值调零，闭合开关S，调节滑动变阻器R1，使电压表的示数等于它的量程Um；然后，保持滑动变阻器R1的滑片位置不变，调节电阻箱R2，使电压表示数等于12Um，读出此时电阻箱R2的有效阻值，若满足R1RV，則此时电压表的内阻可认为 RV＝ R2.

当调节电阻箱R2，使电压表的示数等于12Um时，由电路知识可知，此时电阻箱R2两端的电压大于12Um，即R2>RV，可见，这样测出的结果，将造成电压表RV的测量值偏大.

【例5】实验室可选用器材：①电阻箱1，最大阻值为999999 Ω；②电阻箱2，最大阻值为2 kΩ：③电源E1，电动势约为2 V，内阻不计；④电源E2，电动势约为6 V.内阻不计：另外有开关2个，导线若干，电流表的量程为1 mA，内阻约100 Ω.现采用如图12所示的电路测量电流表的内阻rg.

（1）实验步骤的顺序为   ；

①断开S2，合上S1，调节R，使电流表A满偏；

②再合上S2，调节R1，使电流表A半偏，则rg=R1；

③断开S1，S2，将R调到最大.

（2）可变电阻R1应选择①②中的   （填“①”或“②”）.为使结果尽可能准确，可变电阻R应选   （填“①”或“②”），电源E應选   （填“③”或“④”）；

（3）认为内阻rg=R1，此结果与rg的直实值相比   （填“偏大”“偏小”或“相等”）.

分析：（1）按半偏法测电流表内阻的原理，其步骤为③ ①②.

（2）为了减小实验的误差，应使电阻R的阻值尽量大些，最好使电阻R大于电流表内阻rg100倍以上，所以电阻R选电阻箱1，由闭合电路的欧姆定律估算电源的电动势为： E=Im（rg+R）， 显然，为使R尽量大一点，则电源必须 选E2.

（3）闭合S2，由于多并联了电阻R1，则总电路中的电流增大了，电流表电流为12Ig，但流过R1的电流将大于12Ig，因此，R1的电阻小于rg.

四、电桥法

如图13所示是电桥法测电阻的的实验电路.图中Rx是待测电阻，R是电阻箱，R1、R2是已知阻值的定值电阻.闭合开关S，灵敏电流计的指针发生偏转.再调整电阻箱R的阻值为R0时，使得灵敏电流计的示数为零.

当灵敏电流计的示数为0时，说明灵敏电流计两端电势相等，根据串联电路电流相等的特点，可得：

U R1 R1=U R2 R2，URR0=U Rx Rx

解得：Rx=R2R0R1

由此可知，只要知道R1、R2、R0，利用电桥法可以计算出待测电阻Rx.

【例6】某同学利用如图14所示的电路测量一微安表（量程为100 μA，内阻大约为2 500 Ω）的内阻.可使用的器材有：两个滑动变阻器R1、R2（其中一个阻值为20 Ω，另一个阻值为2 000 Ω）；电阻箱Rz（最大阻值为99 9999 Ω）；电源E（电动势约为15 V）；单刀开关S1和S2.C、D分别为两个滑动变阻器的滑片.

（1）完成下列填空：

①R1的阻值为     Ω（填“20”或“ 2 000 ”）.

②为了保护微安表，开始时将R1的滑片C滑到接近图14中的滑动变阻器的     端（填“左”或“右”）对应的位置；将R2的滑片D置于中间位置附近.

③将电阻箱Rz的阻值置于2 5000 Ω，接通S1.将R1的滑片置于适当位置，再反复调节R2的滑片D的位置.最终使得接通S2前后，微安表的示数保持不变，这说明S2接通前B与D所在位置的电势    （填“相等”或“不相等”）.

④将电阻箱Rz和微安表位置对调，其他条件保持不变，发现将Rz的阻值置于2 6010 Ω时，在接通S2前后，微安表的示数也保持不变.待测微安表的内阻为   Ω（结果保留到个位）.

（2）写出一条提高测量微安表内阻精度的建议：

分析：（1）①要将滑动变阻器R1接成分压电路，则必须选择阻值较小的20 Ω的滑动变阻器；

②为了保护微安表，开始时将R1的滑片C滑到接近图14中滑动变阻器的左端对应的位置；

③将电阻箱Rz的阻值置于2 5000 Ω，接通S1；将R1的滑片置于适当位置，再反复调节R2的滑片D的位置；最终使得接通S2前后，微安表的示数保持不变，这说明S2接通前后在BD中无电流流过，可知B与D所在位置的电势相等；

④设滑动变阻器R2的滑片D两侧电阻分别为R 21 和R 22 ，因B与D所在位置的电势相等，可知；R z1 R 21 =RAR 22 ；同理当Rz和微安表对调后，仍有：RAR 21 =R z2 R 22 ；联立两式解得：RA=R z1 R Z2 =2 500×2 601 Ω=2 550 Ω.

（2）为了提高测量精度，调节R1上的分压，尽可能使微安表接近满量程.

五、欧姆表法

如图15所示是欧姆表的内部结构图，当被测电阻Rx接入电路后，根据闭合电路的欧姆定律可求出通过表头的电流为I=ERg+R1+r+Rx.由此可知，对给定的欧姆表，电路中的电流I与被测电阻Rx具有一一对应的关系，所以，事先在刻度盘上直接标出电阻值，由表头指针的位置就可以知道Rx的大小.

1.直接测量法

【例7】如图16所示，某同学对一段金属导体粗测电阻，金属导体的横截面为空心的等边三角形，内三角形为中空.为了合理选用器材设计测量电路，他先用多用表的欧姆挡“×1”按正确的操作步骤粗测其电阻，指针如图乙，则粗测结果应记为_______  Ω.

分析：从欧姆表的刻度盘上读出的数据是6，则该金属导体的电阻为：

R=6×1 Ω＝6 Ω.

2.间接测量法

【例8】（2000年理科综合）电阻R1，R2，R3，连结成如图17图示的电路，放在一个箱中（虚框所示），箱面上有三个接线柱A、B、C请用多用表和导线设计

一个实验，通过A、B、C的测量，确定各个电阻的阻值，要求

写出实验步骤并用所测值表示电阻R1、R2、R3.

分析：为了测出三个电阻的阻值，可将导线短接电路，使其中的一个电阻被短路，再用多用表测出另二个电阻并联的总电阻.

用导线短接BC，测出A、B两点间的电阻值为Rx，则：

1Rx=1R1+1R2;

用导线短接AB，测出B、C两点间的电阻值为Ry，则：1Ry=1R2+1R3;

用导线短接AC，测出A、C两点间的电阻值为Rz，则：1Rz=1R1+1R3;

解以上三式得：R1=2RxRyRzRxRy+RyRz-RxRz，R2=2RxRyRzRyRz-RxRy+RxRz，R3=2RxRyRzRxRy+RxRz-RyRz.

六、规律法

1.应用闭合电路的欧姆定律

【例9】（1999年上海高考）现有一阻值为100Ω的定值电阻、一个电键、若干根导线和一个电压表，该电压表表面上有刻度但无刻度值，要求设计一个能测定某电源内阻的实验方案，已知电压表内阻很大，电压表量程大于电源电动势，电源内阻约为几欧，要求：

（1）在右边方框中画出实验电路图；

（2）简要写出完成接线后的实验步骤；

（3）写出用测得的量计算电源内阻的表达式r= _____.

分析：由于电压表表盘刻度是均匀的，说明电压表两端的电压与电压表指针偏转数成正比.

所以，可设计如图18所示的实验电路，设电压表偏转1格代表的电压值为U0，当S断开时，记下电压表偏转格数N1，即得电源电动势为N1U0；当S闭合时，记下电压表偏转格数N2，则电阻R两端的电压为N2U0，由闭合电路欧姆定律得流过R的电流：

I=ER+r=N1U0R+r

R两端的电压为：U=I·R=N1U0R+r·R，U=N2U0

解得：r=N1-N2N2·R

2.应用并联电路分流原理

【例10】（1999年全国高考）如图19所示为测量电阻的电路，Rx为待测电阻，R的阻值已知，R′为保护电阻，阻值未知，电源E的电动势未知，S1、S2均为单刀双掷开关.A为电流表，其内阻不计.

测量Rx的步骤为：将S2向d闭合，S1向a闭合，记下

电流表读数I1，再将S2向c闭合，S1向__________闭合，

记下电流表读数I2.

计算Rx的公式是Rx=__________.

分析：该实验通过开关S1、S2使Rx和R组成并联电

路，电流表A分别测出通过Rx和R的电流，从而可得Rx的值.

将S2向d闭合，S1向a闭合，通过电流表的电流I1即为通过Rx的电流，再将S2向c闭合，S1向b闭合，通过电流表的电流I2即为通过R的电流，两种情况下，Rx和R组成同样的并联电路，由并联电路的分流原理得：

I1I2=RRx，整理后得：Rx=I1·RI2.

总之，在测量电阻时，不仅要灵活选用测量电阻的方法，而且要弄清具体的实验条件，这样，就会有效地测出被测电阻的阻值，达到实验的目的.

責任编辑  李平安