包含所有固定阶数 k 树的一类图

翟冬阳 曾德炎

摘 要：图G是k树当且仅当G是一个顶点数为k+1的完全图，或者在图G中能找到度为k的点v，使得与v相邻的k个点构成的点集为团，且G＼v也是一个k树。设G是一个顶点数为n的k树，其中n=pk+p+1，p2。本文构造了一类新的图包含G作为子图。

关键词：k树；完全图；子图

中图分类号：O157.5  文献标识码：A

一、介绍

本文所研究的图都是简单图。在本文中，一个图的阶数是指这个图的顶点的个数。我们用Pm、Km和Km，n表示m阶路、m阶完全图以及m+n阶完全二部图。用Km表示m阶完全图的补图。设H、G为两个简单图，记E（H，G）={uv|u∈V（H），v∈V（G）}。H∪G表示顶点集为V（H）∪V（G），边集为E（H）∪E（G）的图。H∨G表示顶点集为V（H）∪V（G），边集为E（H）∪E（G）∪E（H，G）的图。设v∈V（G），XV（G），那么NX（v）表示在X中與v相邻的点所构成的点集。用G［X］表示在图G中由点集X所诱导的子图。记G＼v=G［V（G）＼v］，G＼X=G［V（G）＼X］。用Km-E（H）表示在Km的基础上删除掉图H对应的边所得到的图。在本文出现，未定义的标记参考文献［1］。

图G是k树当且仅当G是一个顶点数为k+1的完全图，或者在G中能够找到度为k的点v，使得与v相邻的k个点构成的点集为团，且G/v也是一个k树。1树就是我们通常所说的树。在k树中我们把度为k的顶点称为这个k树的耳朵。显然，对于任意一个顶点为n的k树G，若n≠k+1，则都能在某个顶点数为n-1的k树G'的基础上增加一个度为k的新顶点u，让u与G'中某k个阶团中的顶点v1，v2，…，vk均连边构造而成。我们称这个过程为将耳朵u粘贴到团{v1，v2，…，vk}上。设T（k，n）=Kk∨Kn-k。显然，T（k，n）是一个顶点数为n，耳朵数为n-k的k树，并且是同一个团被这n-k个耳朵粘贴。

设G是一个顶点数为n的2树，其中n3，设n≡q（mod3），其中q=0，1，2。我们设n=3p+q，其中q=0，1，2。对于q=0，1，2，分别构造三类图如下：

当n=3p时，G（3p）构造如下：设V（K2p）={v1，…，v2p}，G（3p）是在图K2p的基础上增加新的点x1，…，xp，并让xi与v1，…，v2i连边构造而成，其中1SymbolcB@

iSymbolcB@

p。显然图G（3p）有3p个顶点。当k=3p+1，p3时，G（3p+1）构造如下：设V（K2p+1）={v1，…，v2p+1}，G（3p+1）是在图K2p+1-v2p-2v2p的基础上增加新的点x1，…，xp，并让xi与v1，…，v2i连边构造而成，其中1SymbolcB@

iSymbolcB@

p。显然图G（3p+1）有3p+1个顶点。当k=3p+2，p2时，G（3p+2）的构造如下：设V（K2p+2）={v1，…，v2p+2}，G（3p+2）是在图K2p+2-v2pv2p+2的基础上增加新的点x1，…，xp，并让xi与v1，…，v2i连边构造而成，这里1SymbolcB@

iSymbolcB@

p。显然图G（3p+2）有3p+2个顶点。

曾德炎［45］证明了这三类图分别包含对应顶点数的所有2树作为子图，得到了下面三个定理：

定理1：设G是任意一个顶点数为n的2树，其中n=3p，p1，则G（3p）包含G作为子图。

定理2：设G是任意一个顶点数为n的2树，其中n=3p+1，p3，则G（3p+1）包含G作为子图。

定理3：设G是任意一个顶点数为n的2树，其中n=3p+2，p2，则G（3p+2）包含G作为子图。

设G是一个顶点数为n的k树，其中nk+1。设n≡q（modk+1），其中q=0，1，…，k。为了方便，我们设k=pk+p+q，其中q=0，1，…，k。对于q=0，q=1和2SymbolcB@

qSymbolcB@

k这三种情形，我们分别构造G（k，pk+p），G（k，pk+p+1）和G（k，pk+p+q）三类图如下：

当n=pk+p时，构造G（k，pk+p）如下：设V（Kpk）={v1，v2，…，vpk}，G（k，pk+p）是在Kpk的基础上增加新的点x1，…，xp，并让xi与v1，…，vik连边构造而成，这里1SymbolcB@

iSymbolcB@

p。显然图G（k，pk+p）有pk+p个顶点。当n=pk+p+1时，构造G（k，pk+p+1）如下：设V（Kpk+1）={v1，…，vpk+1}，G（k，pk+p+1）是在Kpk+1-v（p-1）kvpk的基础上增加新的顶点x1，…，xp，并让xi与v1，…，vik连边构造而成，这里1SymbolcB@

iSymbolcB@

p。显然图G（k，pk+p+1）有pk+p+1个顶点。当n=pk+p+q时，这里1SymbolcB@

qSymbolcB@

k，构造G（k，pk+p+q）如下：设V（Kpk+q）={v1，…，vpk+q}，G（k，pk+p+q）是在Kpk+q-vpkvpk+q的基础上增加新的点x1，…，xp，并让xi与v1，…，vik连边构造而成，这里1SymbolcB@

iSymbolcB@

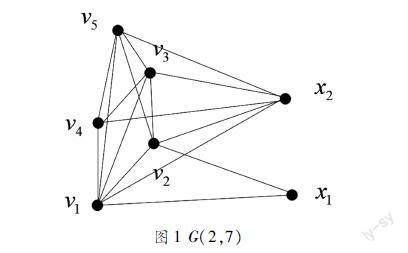
p。显然G（k，pk+p+q）的顶点数为pk+p+q。图1为G（2，7）。

圖1 G（2，7）

最近我们将定理13中关于2树的结论推广到了k树，得到了相应的定理46［6］：

定理4：设G是任意一个顶点数为n的k树，其中n=pk+p，则图G（k，pk+p）包含G作为子图。

定理5：设G是任意一个顶点数为n的k树，其中n=pk+p+1，p3。则图G（k，pk+p+1）包含G作为子图。

定理6：设G是任意一个顶点数为n的k树，其中n=pk+p+q，p2，2SymbolcB@

qSymbolcB@

k。则图G（k，pk+p+q）包含G作为子图。

当顶点数n=pk+p+1时，我们构造了一个新的图Kpk-2∨（K1∨2K2）∪Kp-2，显然该图的顶点数为pk+p+1。记H（k，pk+p+1）=Kpk-2∨（K1∨2K2）∪Kp-2。以下的定理7是本文的主要结论：

定理7：设G是一个顶点数为pk+p+1的k树，其中p2。则H（k，pk+p+1）包含G作为子图。

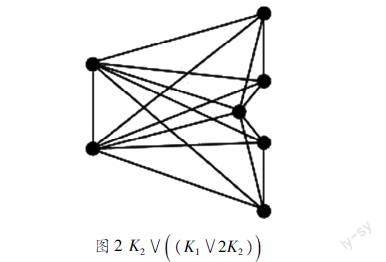
当k=2，p=2时，H（k，pk+p+1）=H（2，7）=K2∨（K1∨2K2），如图2所示。它是包含所有7个顶点的2树作为子图。

图2 K2∨（K1∨2K2）

二、证明

为了证明定理7，我们用到下面这个已知的结论：

定理8［23］：设G是一个n阶的k树。则：

（1）G中的耳朵数大于等于2；

（2）G中度为k的顶点都是G的耳朵；

（3）若G不是顶点数为k+1的完全图，那么在G中的任意两个耳朵均不相邻；

（4）G中不包含长度大于等于4的无弦圈；

（5）G中不包含顶点数为k+2的完全图。

为证明定理7，我们还需要下面的一些引理：

引理1：设G是一个顶点数为2k+3的k树，则存在V′V（G），其中|V′|=k存在整数m满足1SymbolcB@

mSymbolcB@

k，使得G＼V′是Kk+2-m∪K1，m的子图。

证明：设X={u1，u2，…，us}是G中所有耳朵构成的集合。显然，sSymbolcB@

k+3。设H=G＼X。

若s=k+3，则G=T（k，2k+3），且H=Kk。令V′=V（H），则G＼V′=Kk+3。显然，当m=1时，G＼V′是Kk+2-m∪K1，m的子图。

若s=k+2，则H=Kk+1，且在H中有k+1个不同的Kk。由于X中有k+2个顶点，并且每个顶点与H中的一个Kk相邻，则至少存在两个不同的顶点ui，uj∈X，使得NH（ui）=NH（uj）。令V′=NH（ui）=NH（uj），显然G＼V′是K1，k∪K1，1的子图。从而，当m=1时，G＼V′是Kk+2-m∪K1，m的子图。

若sSymbolcB@

k+1，则H是某个顶点数为2k+3-sk+2的k树。设v是H的一个耳朵，其中|NX（v）|=m。由于v不是G的一个耳朵，所以在X中至少有一个顶点与v相邻，即m1。若m=s，由于H中至少有两个耳朵，设u是H的另一个耳朵。因为u也不是G的耳朵，所以|NX（u）|1。不妨设w∈NX（u），由m=s，有w∈NX（v），从而uw、vw∈E（G）。因为w是G的耳朵，有uv∈E（G），从而uv∈E（H）。这与定理8（3）顶点数大于等于k+2的k树中的任意两个耳朵互不相邻矛盾。因此，mSymbolcB@

s-1。由sSymbolcB@

k+1，有mSymbolcB@

k。令V′=NH（v），由于在G中由顶点集NX（v）∪{v}诱导的子图为K1，m，有G＼V′是Kk+2-m∪K1，m的子图。引理得证。

引理2：设G是一个顶点数为n的k树，其中nk+2。若v∈V（G），那么G＼v是某个顶点数为n-1的k树的子图。

证明：我们对n用归纳法。当n=k+2时，由于Kk+1是唯一一个顶点数为k+1的k树，且G-v的顶点数为k+1，从而G-v是Kk+1的子图，也就是说G-v是某个顶点数为n-1的k树的子图。因此引理1对于n=k+2的情形是成立的。假设nk+3，设v是G的一个耳朵，则G-v是一个顶点数为n-1的k树，也就是说引理2对于这种情形成立。因此假设v不是G的耳朵，设u是G的一个耳朵。若v与u相邻，记G1=G-u，则G1是一个顶点数为n-1的k树。因为NG（u）NG（v），所以G＼v是G＼u的一个子图，从而G＼v是某个顶点数为n-1的k树G1的子图。若v与u不相邻，由G＼u是n-1阶k树，根据归纳假设可知，G＼{u，v}是某个顶点数为n-2的k树G2的子图。显然NG（u）V（G2）且在G中由顶点集NG（u）诱导的子图是顶点数为k的完全图。我们在G2的基础上构造一个新图G3。G3是在k树G2的基础上增加一个新的顶点u1，并让u1与NG（u）中的任意一个顶点都相邻。显然G3就是在顶点数为n-2的k树G2的基础上增加了一个新的耳朵u1。也就是说G3是一个顶点数为n-1的k树，同时G＼v是G3的子图。引理得证。

引理3：设G是一个顶点数为n的k树，这里nk+2。设V'V（G），其中V'中顶点的个数为t，这里tSymbolcB@

n-k-1。则G＼V'某个顶点数为n-t的k树的子图。

证明：我们对t用归纳法。由引理2可以得到，引理3对于t=1的情形成立。我们现假设2SymbolcB@

tSymbolcB@

n-（k+1）。设v是V'中的一个点，根据归纳假设可知G＼（V'-v）是某个顶点数为n-（t-1）的k树G1的子图。根据引理2可知G1＼v是某个顶点数为n-t的k树G2的子图。由G-V'是G1-v的一个子图，从而有G-V'也是某个顶点数为n-t的k树G2的生成子图。引理得证。

定理7的证明：设G是一个顶点数为pk+p+1的k树，其中p2。我们对p用归纳法。为了方便描述，在H（k，pk+p+1）=Kpk-2∨（K1∨2K2）∪Kp-2中我们记V（Kpk-2）={v1，v2，…，vpk-2}，V（Kp-2）={x1，x2，…，xp-2}。

若p=2，则H=K2k-2∨（K1∨2K2）。根据引理1，存在V′V（G），其中|V′|=k，存在整数m满足1SymbolcB@

mSymbolcB@

k，使得G＼V′是Kk+2-m∪K1，m的子图。令M=H（k，pk+p+1）＼{v1，v2，…，vk}，则M=Kk-2∨（K1∨2K2）。显然，对于满足1SymbolcB@

mSymbolcB@

k的任意整数m，均有M包含Kk+2-m∪K1，m作为子图。因此，M包含G＼V′作为子图。我们将G中的V′放置到H中的{v1，v2，…，vk}上，由dH（v1）=dH（v2）=…=dH（vk）=2k+2，有H（k，pk+p+1）包含G作为子图。

若p=3，根据引理3，在G中存在一个耳朵u，使得G＼（NG（u）∪{u}）是某个顶点数为2k+3的k树的子图。令M1=H（k，pk+p+1）＼{v1，v2，…，vk，x1}，则M1=K2k-2∨（K1∨2K2），从而M1包含所有2k+3个顶点的k树作为子图。因此M1包含G＼（NG（u）∪{u}）作为子图。我们将G中的点集NG（u）与点u对应放置到H中的点集{v1，v2，…，vk}与点x1上，有H（k，pk+p+1）包含G作为子图。

若p>3，根据引理3，在G中存在一个耳朵u，使得G＼（NG（u）∪{u}）是某个顶点数为（p-1）k+（p-1）+1的k树的子图。令M1=H（k，pk+p+1）＼{v1，v2，…，vk，x1}，则M1=K（p-1）k-2∨（K1∨2K2）∪K（p-1）-2。根据归纳假设M1包含所有（p-1）k+（p-1）+1的个顶点k树的子图，由于G＼（NG（u）∪{u}）是某个顶点数为（p-1）k+（p-1）+1的k树的子图，从而有M1包含G＼（NG（u）∪{u}）作为子图。我们将G中的点集NG（u）与点u对应放置到H中的点集{v1，v2，…，vk}与点x1上，有H（k，pk+p+1）包含G作为子图。证毕。

参考文献：

［1］J.A.Bondy，U.S.R.Murty.Graph Theory With Applications［M］.London：The Macmillan Press，1976.

［2］Bose，P.，Dujmovic，V.，Krizanc，D.，et al.A characterization of the degree sequences of 2trees.J.GraphTheory，2008，58：191209.

［3］D.Y.Zeng，J.H.Yin.On a characterization of ktrees［J］.Czech.Math.J.，2015，65（140）：361365.

［4］曾德炎，翟冬阳.关于2树子图的一些性质［J］.黑龙江科学，2021，14：3539.

［5］曾德炎，翟冬陽.包含所有固定阶数2树作为子图的图的构造［J］.科技风，2021，28：1012.

［6］翟冬阳，曾德炎.包含所有固定阶数k树作为子图的图的构造［J］.科研管理，2022，5：250253.

基金项目：海南省自然科学基金项目“关于可图序列的一类极值问题的研究”（No.122QN335）；青年教师专项培养科研项目“关于两类特殊图蕴含函数的研究”（No.USYQNZX2154）

作者简介：翟冬阳（1989— ），女，汉族，辽宁辽阳人，硕士，讲师，研究方向：图论及其应用的研究；曾德炎（1989— ），男，汉族，湖北荆州人，硕士，副教授，研究方向：图论及其应用。