高频BDS/GPS融合PPP确定2021年玛多MW7.4地震三要素

张怀 聂兆生 刘刚 熊维 倪乙鹏 黄军

摘要：基于GREAT程序，利用GPS和BDS/GPS融合PPP（精密单点定位）获取了2021年玛多MW7.4地震10个高频GNSS测站的地震时间序列，并通过历元间差分法获得了震前30 min的速度时间序列。分析发现，相对于GPS，BDS/GPS速度时间序列在东西、北南、垂直3个方向的精度分别提高了14.8%、15.2%和3.5%。利用STA/LTA（短时窗平均/长时窗平均）方法，从各测站GPS和BDS/GPS时间序列中提取了地震波初至时刻；利用2种时间序列计算得到的震中位置和发震时刻分别为（34.6°N，98.54°E），18：04：28.8和（34.63°N，98.51°E），18：04：29.2（UTC）；利用GPS和BDS/GPS峰值地面位移，根据经验公式反演了玛多地震震级分别为MW7.34和MW7.36，BDS/GPS震级与GCMT公布的结果（MW7.4）更为接近。结果表明：BDS/GPS融合PPP解算可提高时间序列稳定性并降低噪声，更真实地描述震时地表位移变化，从而提高震级解算准确性，更好地为地震预警、地震应急救援等工作提供数据支持。

关键词：BDS/GPS；精密单点定位；地壳形变监测；地震三要素；玛多地震

中图分类号：P315.725   文献标识码：A   文章编号：1000-0666（2023）02-0216-10

doi：10.20015/j.cnki.ISSN1000-0666.2023.0026

0 引言

发震时刻、震中位置和震级大小称为地震三要素，是地震最重要、最基础的3个属性。准确的地震三要素可为地震应急救援、地震危险性研究等工作提供数据支持，其计算的准确性与地表位移的观测精度紧密相关。在地震学观测中，一般采用强震仪和微震仪等传统仪器记录地震波信号。在较大地震发生时，强震仪和微震仪均会出现量程饱和现象（Blewitt et al，2006），导致观测值偏小。另外，由于人为或地震导致的仪器倾斜会在地表位移解算中出现基线偏差（Shu et al，2018），且通过强震仪和微震仪观测值（加速度和速度）计算地表位移时会放大噪声（Blichi et al，2008）。以上因素均会导致地震三要素计算失准。

近年来，众多研究表明GNSS作为一种记录地震信号的强有力工具，可应用于地震地表形变监测、恢复地震波和地震预警等研究（Gao et al，2022；李良发，2019；刘刚等，2014）。GNSS的观测值为位移，可直接监测并记录地震产生的地表位置变化，不会因观测值转化产生误差，在发生大震时也不会出现量程饱和现象，可真实完整记录地震地表形变。许多研究者利用GNSS数据测定地震要素，如Melgar等（2015）针对地震仪存在仪器倾斜和量程饱和等现象，利用6个MW5.9～9.1地震，基于精密单点定位处理了近场及远场共1 321个测站高频GPS数据，得到了利用地面峰值位移计算矩震级的经验公式。Fang等（2020）为了快速确定震级，运用22个震例的高频GPS数据，利用峰值地面速度计算地震震级，所得结果与实际震级偏差为0.26。尹昊等（2018）利用汶川地震7个近场高频GPS数据计算了汶川地震震中位置，与测震学方法得到的震中位置相差15.5 km。姚文敏等（2019）通过2016年新西兰地震定量评估了GNSS峰值地面位移精度对震级估计的影响，指出峰值地面位移精度在2 cm以内时震级误差在0.1以内，且震级对峰值地面位移的敏感度随震中距增大而增加。上述研究均是基于GPS单系统观测数据进行研究的。BDS（北斗卫星导航系统，BeiDou Navigation Satellite System）全球组网完成为多系统观测值融合解算应用于地震地壳形变监测提供了前所未有的契机。相关研究表明：BDS/GPS双系统融合解算可显著提高可视卫星数、增强卫星空间几何结构，从而提高定位精度（Li et al，2015；祝会忠等，2020；魏二虎等，2018）。

本文利用GREAT程序，对2021年玛多MW7.4地震震中附近区域10个高频GNSS连续站观测数据进行BDS、GPS单系统，BDS/GPS双系统PPP（精密单点定位）动态解算，分析了GPS单系统及融合PPP动态时间序列震前和震时两时段的精度，并计算得到了2021年玛多MW7.4地震的三要素。GREAT程序是武汉大学李星星教授团队设计研发的一款卫星大地测量与多源导航软件，包含多系统实时精密單点定位、卫星轨道、钟差精密产品生成、低轨增强GNSS等功能，具有标准化、模块化等特点（Li et al，2020）。

1 BDS/GPS融合PPP解算方法

1.1 玛多地震高频数据

2021年5月22日青海省玛多县发生MW7.4地震（此震级为全球矩心矩张量工作组发布，简称GCMT）。中国地震局地震研究所在第一时间奔赴震区进行地震应急GNSS观测，共获取10个高频GNSS连续测站观测数据，其采样率为1 s。图1为玛多地震震中附近区域连续站点分布图，图中CORS站为连续运行卫星定位服务参考站，可观测GPS、BDS两个系统的卫星。

1.2 BDS/GPS融合PPP观测模型

电离层延迟误差是影响PPP定位精度的重要误差之一。对于电离层延迟误差，本文采用双频非电离层组合模型，可消除电离层延迟一阶项影响。BDS/GPS融合PPP无电离层相位L和伪距P组合模型如下：

LGr=ρGr+ctG+λGIF（NGr+BGr-Bs，G）+TGr+εGr（1）

PGr=ρGr+ctG+c（bGr-bs，G）+TGr+eGr（2）

LCr=ρCr+ctC+λCIF（NCr+BCr-Bs，C）+TCr+εCr（3）

PCr=ρCr+ctC+c（bCr-bs，C）+TCr+eCr（4）

式中：下标r表示接收机；上标G和C分别代表GPS和BDS；ρ为接收机至卫星的几何距离；t为接收机与卫星钟差的差值；λIF为无电离层组合相位观测值的波长；N为无电离层组合的模糊度；br和bs分别为接收机和卫星的测距码延迟，Br和Bs分别为接收机和卫星的相位延迟；T为对流层延迟误差；ε和e分别是相位和伪距的其他测量误差。

1.3 数据处理策略

本文基于BDS/GPS高频观测数据，利用武汉大学发布的精密星历、精密钟差等精密产品对卫星轨道及钟差进行改正，对其它测量误差采用模型或常数进行改正，最终得到ITRF 2014参考框架下的测站三维坐标。其中，GNSS高频观测数据使用Trimble R9s接收机观测得到，可接收BDS-2 B1/B2频段信号和GPS L1/L2频段信号，高度截止角设为10°。采用常用的高度角加权方法确定同星座不同观测值的权值。为了评估BDS与GPS在BDS/GPS融合PPP中的作用，对不同星座间的观测值采用等权。对固体潮汐、海洋潮汐、相对论效应等误差采用模型进行改正。GPS卫星和接收机天线相位中心偏移和天线相位中心变化改正可采用国际GNSS服务（Internutional GNSS Service，IGS）提供的ANTTEX文件进行改正，但IGS只提供了BDS的卫星端天线相位中心偏移改正，未提供卫星端及接收机端的其它改正。对流层延迟干分量通过先验模型改正，湿延迟分量则利用随机游走过程进行估计。测量噪声包括相位缠绕、相对论影响和天线相位中心偏差和变化等，可通过现有模型进行改正。系统间偏差（bCr-bGr）可作为常数估计，相位延迟BGr和BCr可被模糊度参数吸收。

2 BDS/GPS融合PPP获取玛多地震动态形变

2.1 BDS/GPS时间序列

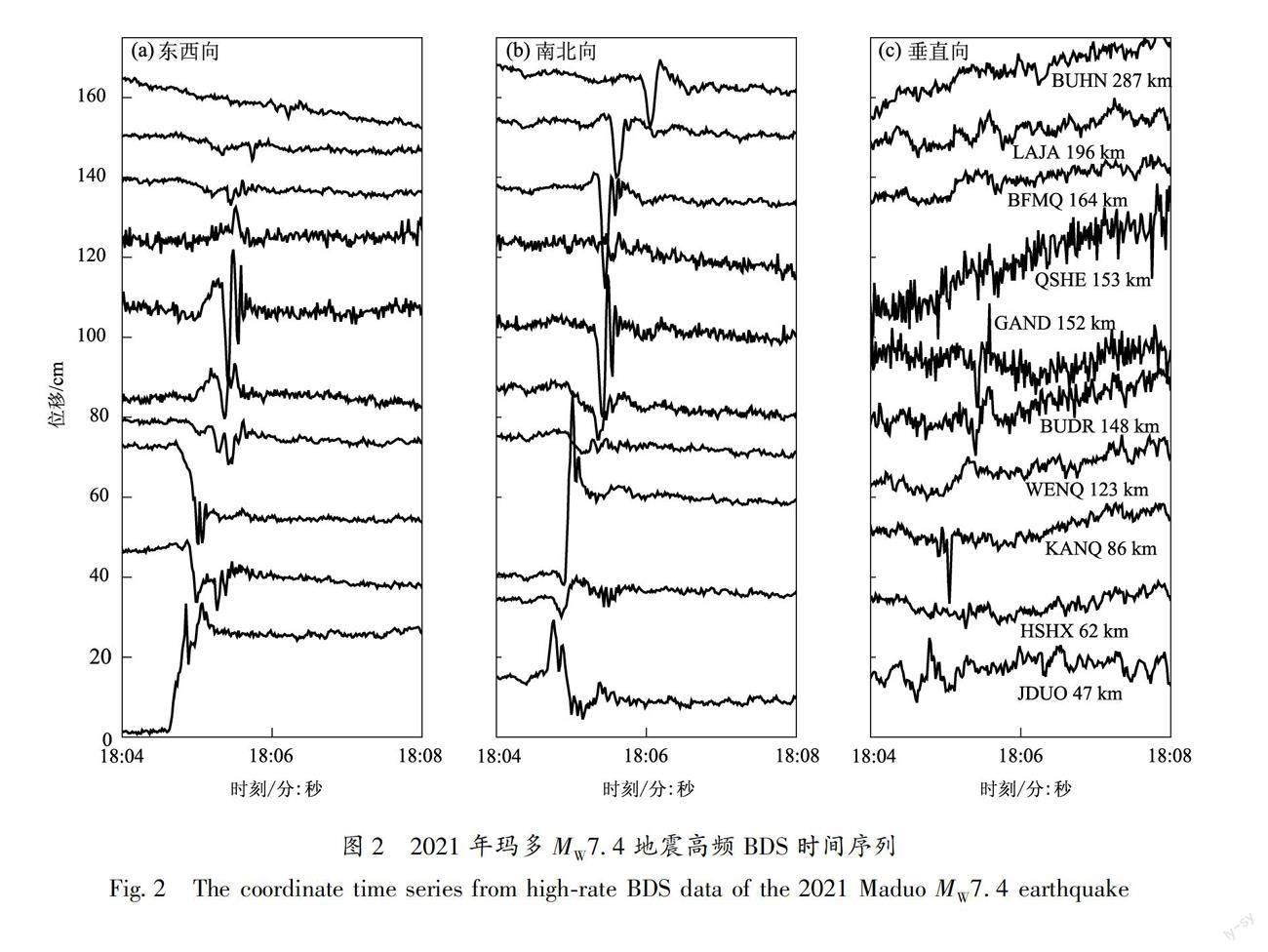
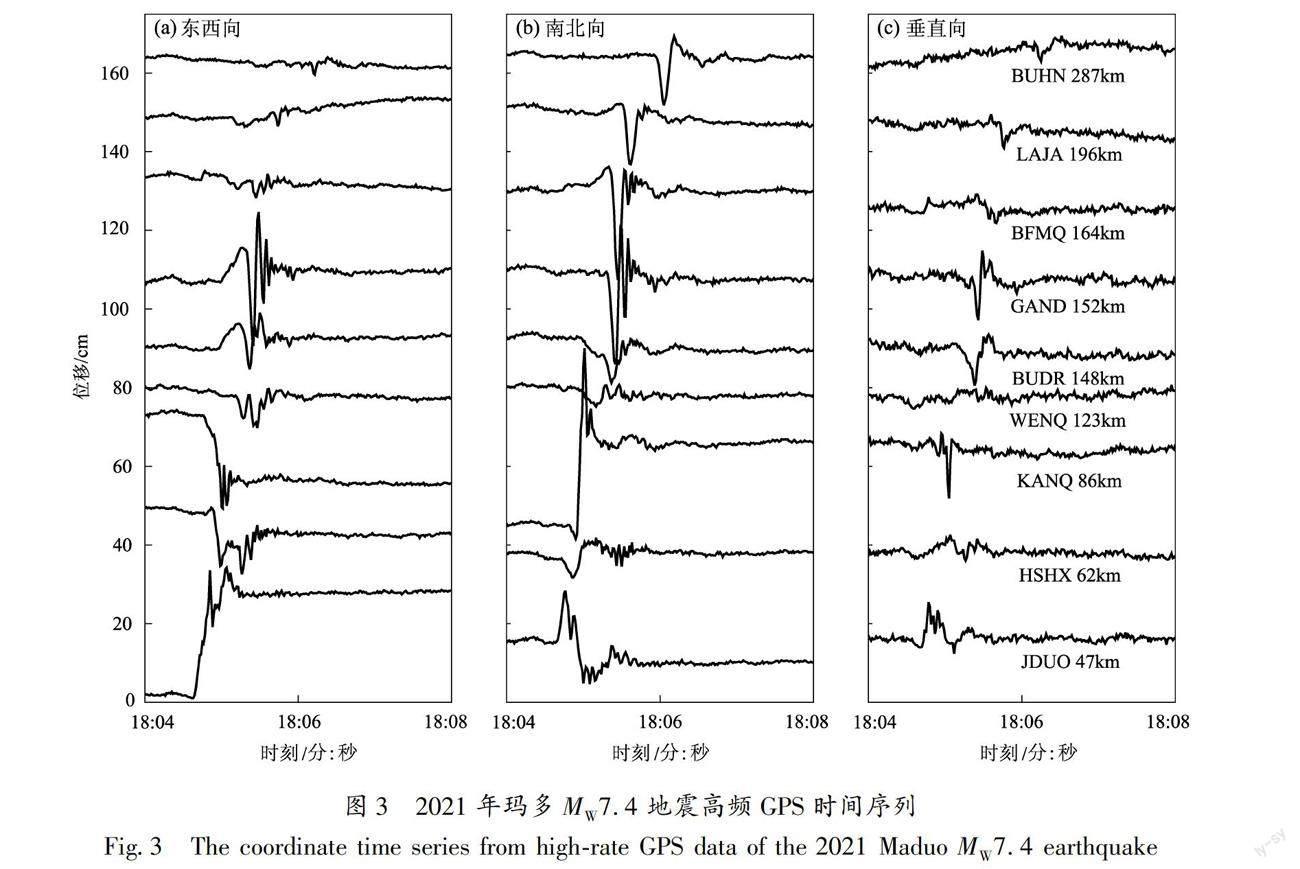
本文首先利用GREAT程序对青海10个CORS站观测数据进行动态PPP解算，分别得到了2021年玛多MW7.4地震时各测站的BDS、GPS和BDS/GPS在东西、北南、垂直3个方向上的时间序列（图2～4）。QSHE测站由于GPS观测数据质量较差，在GPS单系统PPP中未成功记录到真实地震地表位移，因此未在图3中给出其时间序列。

从图2～4可以看出，BDS、GPS和BDS/GPS融合PPP均可以描述震时地表位移随时间的变化。即使距震中约290 km的测站仍可以记录到地震形变信号。距震中最近的JDUO测站（距震中47 km）最先接收到地震波信号，并记录到了约27 cm的地震永久地表形变。KANQ和HSHX等测站也均记录到了较大的永久地表形变。但是BDS单系统时间序列波动较大，且当某一系统观测数据质量较差无法记录地震形变信号时，BDS/GPS仍可保持良好的定位性能，满足地震形变监测需求。

2.2 GPS及BDS/GPS动态时间序列精度分析

为了评估GPS和BDS/GPS时间序列的稳定性及噪声大小，本文通过历元间差分方法，利用高频（1 Hz）GNSS测站坐标时间序列获得各测站GPS和BDS/GPS在东西、南北、垂直3个方向的高频速度时间序列，计算得到了各测站GPS和BDS/GPS速度时间序列在震前30 min的均方根（RMS值），从表1可以看出，玛多地震前30 min，GPS的速度时间序列在3个方向的RMS值分别为2.7、3.3和5.8 mm/s；BDS/GPS的速度时间序列在3个方向的RMS值均有所减小，分别为2.3、2.8和5.6 mm/s，精度分别提高了14.8%、15.2%和3.5%。速度时间序列可表现各测站GPS和BDS/GPS时间序列的稳定性及其噪声。测站速度时间序列的RMS值越小，表明其时间序列稳定性越强、噪声越小。

BDS/GPS时间序列的稳定性及噪声表现优于GPS主要是由于BDS/GPS双系统的可视卫星数更多，其卫星空间几何结构更好。图5以LAJA站为例，给出了GPS单系统及BDS/GPS双系统可视卫星数量及几何精度因子（GDOP值）。从图中可以看出：BDS/GPS融合PPP可显著提高可视卫星数，增强卫星空间几何结构及其稳定性，从而提高定位精度。在地壳形变监测中，BDS/GPS时间序列可发挥其精度高、稳定性强的优势。

3 用BDS/GPS测定玛多地震三要素

3.1 地震波初至时刻提取

准确提取地震波初至时刻是计算地震发震时刻和震中位置的关键，本文应用短时窗平均/长时窗平均法（STA/LTA）（Allen，1978）提取地震波初至时刻，选用历元间差分函数作为特征函数：

CF（i）=f（i）-f（i-1）（5）

式中：f（i）為i时刻各方向坐标。短时窗主要表示特征函数在短时间内的变化情况，长时窗则表示信号在当前时段内的平均噪声水平。当检测到地震波信号时，短时窗特征函数的平均值与长时窗平均值的比值会明显增大，当某一时刻长、短时窗的特征函数值比值大于设定的阈值时，则认为地震波到达。

为了更准确地提取地震波初至时刻，本文选取了多种长、短时窗长度和阈值组合，将长时窗分别设置为50～70 s，步长为5 s；短时窗分别设置为5～20 s，步长为1 s；STA/LTA阈值分别设置为1.8～2.8，步长为0.1。通过不同组合提取地震波初至时刻后发现，长、短时窗长度及阈值的选取需要根据GNSS地震时间序列设定。当长时窗长度较小时，LTA值可能会随时间变化较明显，无法表现出GNSS时间序列的一般特性。当短时窗长度较小时，STA值对地震信号较为敏感，随时间波动较大，可能会将一般噪声识别为地震信号；而短时窗的长度较大时，其STA值不能较为真实地描述地震信号在某一瞬间的变化状态。

最终，本文选用的长时窗长度为70 s，短时窗长度为9 s，阈值为2.2。利用STA/LTA法提取的各测站地震波初至时刻见表2，其中本文涉及到玛多地震的时间，使用的是国际标准时间。从表2可看出，在更加稳定的KANQ测站的BDS/GPS时间序列中可更早探测到地震波信号。

3.2 震中位置及发震时刻反演

本文采用距离交会法确定地震震中，假设地震的震中坐标为（X，Y，Z），则各测站到震中的距离Di可表示为：

Di=（Xi-X）2+（Yi-Y）2+（Zi-Z）2（6）

假定地震波在地壳中各个方向的传播速度v是相同的，则根据地震波初至时刻和各台站之间的距离可得如下观测方程：

D2-D1-v（t2-t1）=0D3-D1-v（t3-t1）=0Dn-D1-v（tn-t1）=0（7）

对上述观测方程进行线性化，通过最小二乘迭代后可计算得到震中和地震波传播速度v。为了加快计算速度，本文将第一个接收到地震波信号的测站坐标记为震中位置的初值。在地震研究中，GNSS测站接收到的地震波一般为S波（波速3～4 km/s），本文分别使用不同波速（3～4 km/s，步长为0.1 km/s）进行计算，最终地震波速度v设为3.2 km/s。地震发震时刻T0可根据上一步中得到的震中坐标（X，Y，Z）和地震波速度计算求得。为了减少计算误差，可对其取平均值：

T0=∑ni=1（ti-Div）n（8）

式中：Di为第i测站至震中的距离；ti为第i测站的地震波初至时刻。

根据玛多地震的GPS和BDS/GPS地震时间序列（图2～4）以及各测站地震波初至时刻（表2），得到了2021年玛多地震的GPS和BDS/GPS地震震中位置和发震时刻分别为（34.6°N，98.54°E），18：04：28.8；（34.63°N，98.51°E），18：04：29.2。

从图6可以看出，本文计算所得震中位置与中国地震台网、GCMT等机构发布的震中位置比较接近（表3）。本文使用BDS/GPS时间序列所得震中位置与GCMT发布的震中位置相差5.8 km，所得发震时刻与GCMT发布结果（18：04：29.2）一致，使用GPS时间序列震中位置与GCMT发布震中位置相差10 km，所得发震时刻与GCMT结果相差0.4s；使用BDS/GPS时间序列所得震中位置与中国地震台网发布的震中位置相差17.4 km，所得发震时刻与中国地震台网发布结果（18：04：11）相差18.2 s，使用GPS时间序列所得震中与中国地震台网发布的震中位置相差20 km，发震时刻与中国地震台网结果相差17.8 s。利用BDS/GPS时间序列计算的震中位置和发震时刻更加接近实际震中位置与发震时刻。

3.3 震级确定

日本学者（Kanamori，1977；Hanks，Kanamori，1979）提出了矩震级的概念。矩震级不是利用地震记录波形的振幅来计算震级，而是通过地震矩来确定震级。地震矩是通过GNSS或InSAR等方法获得地表平均滑动后获得的。应用矩震级来表征地震的大小比较准确，但是需要大量复杂计算得到，耗时较大。

Gutenberg（1945）推导出了地震面波最大水平位移、震中距和地震震级的经验关系公式为：

M=log（PGD）+1.66log（R）+2.0（9）

式中：M为地震震级；PGD为根据地震面波计算得到的测站峰值地面位移，其单位为μm；R是测站至震中的距离，单位用“°”表示。Fang等（2014）利用3个大地震的高频（1 Hz）GPS数据验证了古登堡面波震级经验公式对GPS数据的可用性，得出该公式对GPS数据同样适用，由高频GPS计算得到的PGD同样可以得到准确的震级。

PGD可通过BDS/GPS融合PPP地震時间序列提取东西向、南北向的地震波形振幅后得到，计算公式为H=E2+N2，E和N分别为东西向和南北向地震波形振幅。在实际应用中，可对BDS/GPS融合PPP地震时间序列每个历元的E和N作计算得到H值。图7以KANQ测站为例，计算了其各历元H值并提取PGD，得到PGD为50.17 cm。

计算每个测站各历元H值并提取得到各测站的峰值地面位移后，可利用峰值地面位移PGD根据式（9）计算地震震级。本文利用所有测站峰值地面位移估计的震级见表4。

从表4中可以看出，由于QSHE测站GPS观测数据质量较差，利用其峰值地面位移计算得到震级为MW8.28，与GCMT公布的震级相比偏大，因此QSHE测站不参与后续各测站平均震级计算。对剩余9个测站GPS和BDS/GPS震级取平均值后，得到平均GPS震级为MW7.34，与GCMT公布的震级相差0.06；平均BDS/GPS震级为MW7.36，与GCMT公布的震级相差0.04。从上可以看出，使用BDS/GPS比使用GPS峰值地面位移估算的震级更加接近公布震级。

利用峰值地面位移估算的震级呈现出方向性特征，震级在断层破裂扩展方向偏大，在非断层破裂扩展方向偏小。例如，距离震中最近的JDUO和HSHX测站，用GPS数据估算震级为MW6.89和MW6.8，用BDS/GPS数据估算震级为MW6.91和MW6.79，相比GCMT公布的震级MW7.4偏小；在地震断层破裂扩展方向上的KANQ和GAND测站，用GPS数据估算震级为MW7.52和MW7.69、用BDS/GPS数据估算震级为MW7.53和MW7.69，比GCMT公布的震级偏大。笔者分析发现，这主要与地震断层破裂的方向性效应和地震波方向性效应有关。Somerville 等（1997）研究表明地震波传播方向与地震断层破裂方向夹角越小时，其地震动幅值越大。玛多地震为典型的左旋走滑型地震，其破裂沿昆仑山口—江错断裂展布长约160 km，其走向约为295°（王迪晋等，2022）。据此可以看出，位于昆仑山口—江错断裂及其延长线上的KANQ、GAND和BFMQ等测站具有更大的PGD值从而得到了偏大的震级，而远离昆仑山口—江错断裂及其延长线的WENQ、JDUO和HSHX等测站的PGD偏小，因此震级也偏小。从图6可以看出，此次获取的GNSS连续站大部分分布于断层破裂扩展方向两侧，因此用所有测站PGD估计的震级均偏小。

本文在利用PGD估算震級时，只考虑了测站震中距及地震时间序列的PGD，未考虑地震断层破裂的方向性效应与地震波方向性效应。且由于各测站所处地壳结构、基岩性质以及测站高度等影响，不同测站利用地震时间序列的PGD估算得到的震级与公布震级有微小的偏差。根据以上分析，为了用PGD估算得到更准确震级，克服地震断层破裂的方向性效应与地震波方向性效应以及不同测站的地壳地质差异影响，在估计震级时应尽量在震中周围均匀地选取尽可能多的测站进行估计，并采用多星座数据联合解算获取更真实的震时地表位移。

4 结论

本文利用2021年玛多MW7.4地震的高频GNSS观测数据，对震前30 min和包含地震信息的GPS和BDS/GPS融合PPP时间序列进行了分析，并计算了玛多地震的地震三要素，得到如下结论：

（1）通过历元间差分法获取震前30 min速度时间序列，得出GPS速度时间序列在东西、北南、垂直3个方向上的RMS值分别为2.7、3.3和5.8 mm/s；BDS/GPS速度时间序列在3个方向的RMS值分别为2.3、2.8和5.6 mm/s，精度分别提高了14.8%、15.2%和3.5%。BDS/GPS可提高可视卫星数并增强卫星空间几何结构，从而显著提高定位精度及其动态解算稳定性。

（2）利用GPS地震时间序列计算得到玛多地震发震时刻为18：04：28.8，震中位置为（34.60°N，98.54°E），震级为MW7.34；BDS/GPS地震时间序列计算得到的玛多地震发震时刻为18：04：29.2，震中位置为（34.63°N，98.51°E），震级为MW7.36。由BDS/GPS得到的地震三要素更加准确，更接近GCMT公布的结果。

（3）由于地震断层破裂的方向性效应和地震波以及本文获取的GNSS测站位置分布不均匀，导致沿地震断层破裂方向的测站估算的震级偏大，从而使整体估算震级与GCMT的震级相比偏小。在今后的地震三要素解算中，可采用分布均匀的测站并使用BDS/GPS融合PPP保证地震三要素的准确性，从而更好地为地震预警、地震应急救援等工作提供技术支持和数据保障。

野外数据采集工作人员辛苦付出，武汉大学测绘学院李星星团队提供了GREAT程序，武汉大学卫星导航定位技术研究中心提供了精密产品，在此一并表示感谢。

参考文献：

李良发.2019.高精度北斗数据处理及地形变监测应用［D］.武汉：中国地震局地震研究所.

刘刚，聂兆生，方荣新，等.2014.高频GNSS形变波的震相识别：模拟实验与实例分析［J］.地球物理学报，57（9）：2813-2825.

王迪晋，王东振，赵斌，等.2022.2021年青海玛多MW7.4地震GNSS同震形变场及其断层滑动分布［J］.地球物理学报，65（2）：537-551.

魏二虎，刘学习，王凌轩，等.2018.BDS/GPS组合精密单点定位精度分析与评价［J］.武汉大学学报（信息科学版），43（11）：1654-1660.

姚文敏，方荣新，王珍，等.2019.高频GNSS观测快速估计地震震级及其精度评估［J］.大地测量与地球动力学，39（12）：1249-1253.

尹昊，单新建，张迎峰，等.2018.高频GPS和强震仪数据在汶川地震参数快速确定中的初步应用［J］.地球物理学报，61（5）：1806-1816.

祝会忠，杨添宇，赵洪涛，等.2020.GNSS多系统精密单点定位方法与性能分析［J］.测绘科学，45（12）：1-7，21.

Allen R V.1978.Automatic earthquake recognition and timing from single traces［J］.Bulletin of the Seismological Society of America，68（5）：1521-1532.

Bilich A，Cassidy J F，Larson K M.2008.GPS seismology：application to the 2002 MW7.9 denali fault earthquake［J］.Bulletin of the Seismological Society of America，98（2）：593-606.

Blewitt G，Kreemer C，Hammond W，et al.2006.Rapid determination of earthquake magnitude using GPS for tsunami warning systems［J］.Geophysical Research Letters，33（11）：L11309.

Fang R X，Shi C，Song W W，et al.2014.Determination of earthquake magnitude using GPS displacement waveforms from real-time precise point positioning［J］.Geophsical Journal International，196（1）：461-472.

Fang R X，Zheng J W，Geng J H，et al.2020.Earthquake magnitude scaling using peak ground velocity derived from high-rate GNSS observations［J］.Seismological Research Letters，92（1）：227-237.

Gao Z Y，Li Y C，Shan X J，et al.2022.Testing a prototype earthquake early warning system：A retrospective study of the 2021 MW7.4 Maduo，Tibet，earthquake［J］.Seismological Research Letters，93（3）：1650-1659.

Gutenberg B.1945.Amplitudes of surface waves and magnitudes of shallow earthquakes［J］.Bulletin of the Seismological Society of America，35（1）：3-12.

Hanks T C，Kanamori H.1979.A moment magnitude scale［J］.Journal of Geophysical Research，84（B5）：2348-2350.

Kanamori H.1977.The energy release in great earthquakes［J］.Journal of Geophysical Research，82（20）：2981-2987.

Li X X，Zhang X H，Ren X D，et al.2015.Precise positioning with current multi-constellation Global Navigation Satellite Systems：GPS，GLONASS，Galileo and BeiDou［J］.Scientific Reports，5（1）：8328.

Li X X，Zhu Y T，Zheng K，et al.2020.Precise orbit and clock products of Galileo，BDS and QZSS from MGEX since 2018：comparison and PPP validation［J］.Remote Sensing，12（9）：1415.

Melgar D，Crowell B W，Geng J H，et al.2015.Earthquake magnitude calculation without saturation from the scaling of peak ground displacement［J］.Geophysical Research Letters，42（13）：5197-5205.

Richter C F.1935.An instrumental earthquake magnitude scale［J］.Bulletin of the Seismological Society of America，25（1）：1-32.

Shu Y M，Fang R X，Geng J H，et al.2018.Broadband velocities and displacements from integrated GPS and accelerometer data for high-rate seismogeodesy［J］.Geophysical Research Letters，45（17）：8939-8948.

Somerville P G，Smith N F，Graves R W，et al.1997.Modification of empirical strong ground motion attenuation relations to include the amplitude and duration effects of rupture directivity［J］.Seismological Research Letters，68（1）：199-222.

Determination of Three Parameters of the 2021 MaduoMW7.4 Earthquake Using High-rate BDS/GPS

ZHANG Huai1，NIE Zhaosheng1，LIU Gang1，XIONG Wei1，NI Yipeng1，HUANG Jun2

（1.Institute of Seismology，China Earthquake Administration，Wuhan 430071，Hubei，China）

（2.Helongjiang Provincial Gedogy and Mineral Resources Test and Application Inshitute，Harbin 150036，Heilongjiang，China）

Abstract

The seismic time series of 10 high-rate GNSS stations during the 2021 Maduo MW7.4 earthquake were acquired using GPS and BDS/GPS fusion PPP based on the GREAT program，and the velocity time series 30 minutes before the earthquake were obtained based on the variometric approach.The analysis found that the BDS/GPS relative to GPS velocity RMS values in the EW，NS and UP orientation can be improved by 14.8%，15.2% and 3.5% respectively.The seismic waves first arrival-time was extracted from the BDS/GPS time series of each station using the STA/LTA method，the location of the epicenter of the Maduo earthquake was（34.63°N，98.51°E），and the earthquakes original time was 18：04：29（UTC），calculated from the time of first arrival of seismic waves at each station.This article refers to the time of the Maduo earthquake，using the Coordinated Universal Time.The epicenter of the Maduo earthquake calculated by GPS time series is（34.6°N，98.54°E），and the original time is 18：04：28.8.Using GPS and BDS/GPS peak ground displacement，the Maduo earthquake magnitude was inverted according to the empirical formula，and the obtained magnitudes were MW7.36 and MW7.34，respectively.The BDS/GPS magnitude was closer to the result published by GCMT.The results show that the BDS/GPS fusion PPP solution can improve the stability of time series and reduce noise，which can more realistically describe the surface displacement changes during the earthquake，thus improving the accuracy of the magnitude solution and providing better data support for earthquake early warning and post-earthquake rescue.

Keywords：BDS/GPS；PPP；crustal deformation monitoring；three parameters of an earthquake；Maduo earthquake

收稿日期：2022-05-16.

基金項目：国家自然科学基金项目（42074015，41874018）；中国地震局星火计划攻关项目（XH20038）；科技部研发专项（2018YFE0206100）.

第一作者简介：张 怀（1997-），硕士研究生在读，主要从事地震大地测量研究.E-mail：huaizhang_97@163.com.

通讯作者简介：聂兆生（1982-），正研级高级工程师，主要从事大地测量观测技术在地震监测预报中的应用研究.E-mail：niezhaosheng@126.com.

张怀，聂兆生，刘刚，等.2023.高频BDS/GPS融合PPP确定2021年玛多MW7.4地震三要素［J］.地震研究，46（2）：216-225，doi：10.20015/j.cnki.ISSN1000-0666.2023.0026.

Zhang H，Nie Z S，Liu G，et al.2023.Determination of three parameters of the 2021 Maduo MW7.4 earthquake using high-rate BDS/GPS［J］.Journal of Seismological Research，46（2）：