让图形概念的建构走向深入
代胜 朱艳

“三角形的认识”是人教版数学四年级下册第五单元的教学内容。本节课注重引导学生聚焦图形的特征及概念本质,深入认识三角形。
一、借助“说明书”,经历三角形定义的形成过程
三角形的认识分直观辨认和概念理解两个阶段。教学《三角形的认识》时,笔者设置了这样的任务:先画一个三角形,再将画三角形的过程写成说明书。学生都能画出三角形,但对画三角形的过程的描述缺乏逻辑性。笔者收集了学生有代表性的作品,并进行了如下交流。
师:下面两份说明书有什么相同点和不同点?1号说明书写明:画三条线,并将它们连在一起。2号说明书写明:画三条线段,线段的端点要连在一起。
生1:两份说明书都写明要画三条线,但1号只说“连在一起”,2号却说“端点要连在一起”。
生2:2号的说法更规范,线有线段、直线、射线,三角形的三条边都是线段。
生3:1号没说清楚“连在一起”是连线还是连点,2号强调了要连“端点”。
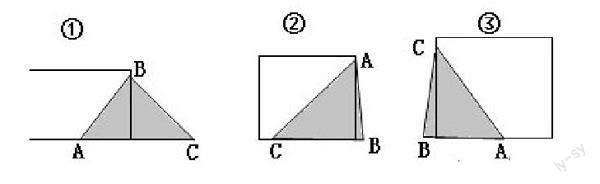
师:下面三个图形都是三角形吗?
生4:这三个图形都不是三角形,①号有一条线段出头了;②号只连了三条线段的一个端点,另一个端点没连;③号上面两条线段的端点没有连起来。
师:再来看看3号说明书,上面写着“画三条线段,形成三个角的图形就是三角形”,你有什么想法?
生5:3号说明书说了线段,还说了角,很全面。
生6:②号图形有三个角,但它不是三角形。这说明3号说明书有问题。
师:2号说明书可以怎样改进?
生7(指三角形的其中一条线段):这条线段有两个头,每个头要连不同的线段。
师:教材上三角形的定义中的“围成”和“每相邻两条线段的端点相连”是什么意思?书上的说明和刚才同学们的说法有什么相似的地方?
生8:“围成”就是围一圈;“每个头要连不同的线段”就是“相邻线段的端点相连”。
学生经历了给画三角形的过程写说明书并逐步修正与完善的过程,使浅层次的经验得到提升,从而对三角形概念的理解逐渐趋向本质。
二、创设情境,体会三角形高的存在价值
底和高是对三角形的定量刻画。底在三角形中是实实在在的线段,学生容易理解,但高是虚拟的线段,学生很难体会到高存在的价值。
课堂上,笔者先创设问题情境:“某厂家要为一些三角形材料定做长方体外包装盒(三角形材料必须有一边靠着盒子的棱),如果厚度忽略不计,包装盒要怎样设计,才能将三角形材料装进去?先想一想,再画一画。”学生交流后发现:长方体包装盒的长和宽不仅与三角形三条边的长度有关,还与最高点到底边的距离有关。接着,笔者选取学生设计的有代表性的长方体包装盒(忽略厚度)贴在白板上(如下图),引导学生将三角形放上去比划并思考:怎样摆放能看出最高点与底边的距离,进而确定长方体包装盒是否能装下三角形材料。
学生操作后发现:无论以哪条边为底,都要将顶点与长方体包装盒的宽重合,再将三角形最高点到底边的垂直距离与长方体的宽作比较。笔者顺势揭示三角形的底和高的概念,引导学生在图中找出三角形的“一个顶点”“它的对边”及“垂足”的位置。
当学生对三角形的高有一定的理解之后,笔者提问:厂家为了节省材料,想将包装盒尽量做得小一些,上面的包装盒还可以怎样改进?学生小组交流后汇报:包装盒的长以AC为标准,宽就是B到AC的距离;将CB的长度作为包装盒的长,则要以A到CB的距离为宽;将BA的长度作为包装盒的长,则BA边上的高就是宽。还有学生指出:包装盒的长和宽要对应起来,三角形的一个底对应一条高,不能混淆。笔者乘机追问:你认为三角形有几条高?为什么?有的学生从底的角度来思考:三角形的每条边都可以作底,三角形有三条边,就有三条对应的高;有的学生从顶点的角度解释:三角形有三个顶点,每个顶点都能摆到最高点的位置,对应三个不同的高度,所以三角形有三条高。笔者追问:每个三角形都有三条高吗?你能找出下面两个三角形(出示一个直角三角形和一个钝角三角形)的底对应的高吗?学生兴奋地分享自己的发现:直角三角形中,直角可以直接靠着长方体包装盒的一组长与宽摆放,组成直角的两条边以一条边为底,另一条边就是高。对于钝角三角形高的研究,学生出现了困惑:三角形的高应该在三角形的内部,而钝角三角形有两个顶点到底边的距离不在三角形内部,能称之为高吗?笔者引导学生利用三角形底与高的定义进行辨析,让学生体会到“不管这条线段在什么位置,只要是从顶点到对边的距离,都是三角形的高”。
三、在找高过程中击破三角形高的画法难点
画三角形高的过程与过直线外一点作已知直线的垂线段本质相同,难度却大大增加。教学中,笔者引导学生将画高的过程与找高的过程进行联结,逐个击破画高难点。
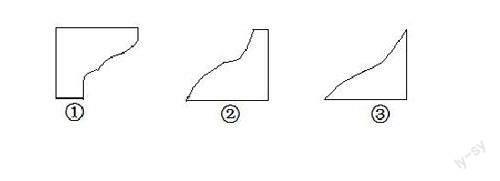
师:如下图,某厂家设计的包装盒(忽略厚度)被损毁了一部分,你认为下面这三个包装盒能帮我们找到三角形ABC的高吗?
生1:①号左边的宽没有破损,将三角形ABC的一条边贴着包装盒的下边放,最高点到下边的距离就是高。
生2:将①号盒的上边转到最下面,包装盒的长和宽都没有损毁,将三角形的最高点靠上去,底与长重合就可以了。
生3:②号和③号也可以,只要还有一个直角没破损,就能找到高。
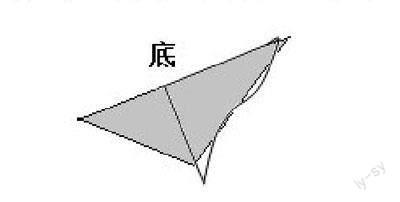
师:怎么转?旋转到什么位置能顺利画出高?
生4:以③号包装盒为例,如下图所示,破损的包装盒有一条直角边要作底,必须靠着三角形的底,另一条直角边要转到三角形的顶点位置。
师:生活中有时候找不到这样的包装盒,我们还可以借助哪些工具找三角形的高?
生5:三角尺、書、作业本都可以画高。只要是有直角的工具,都可以画高。
师:给三角形画高跟以前学习的哪个知识点类似?
生6:过直线外一点作已知直线的垂线。
师:“直线外一点”是一个点,“已知直线”是一条直线,三角形有三条边,三个顶点,如果指定三角形的一条边为底,怎么找到“目标点”和“目标线”?
生7:可以想象将三角形的底转到最下面,再找最高点。
生8:不转也可以,“目标线”就是三角形的底,“目标点”就是底对着的顶点。
生9:三角形的底有两个端点,这两个点可以排除,剩下一个点就是目标点。
在这样的活动中,学生对三角形高的概念有了更清晰的认识,对画高工具的工作原理也有了本质理解。
(作者单位:代胜,宜城市教研室;朱艳,宜城市南街小学)
责任编辑 张敏

