住房价格、劳动力流动与制造业转移关系再研究

杨立勋 张志强 陈凯达

[摘要]在拓展的“中心—外围”模型中引入住房价格，分析住房价格及生存黏性对制造业转移的影响机理，利用2002—2020年35个大中城市面板数据，运用面板门限模型进行实证分析。研究发现：（1）城市相对住房价格与制造业相对就业规模间存在倒“U”型的非线性关系。（2）以制造业劳动力年均工资收入与所居城市住房价格的比值刻画的“生存黏性”与城市制造业相对就业规模显著正相关，揭示以劳动力为载体的制造业转移内在动因。提出优化资源配制、“因城施策”、实施区域制造业发展战略等建议。

[关键词]住房价格；劳动力流动；制造业转移；面板门限模型

一、 引言

城镇住房制度改革、住房分配货币化政策实施以及房地产市场建立，为中国房地产业高速发展注入了内生动力。中国房地产业发展为城镇居民住房条件改善、城镇化发展及缓解社会就业压力作出了突出贡献。然而，一方面城市房地产业快速增长助推城市，尤其是一线城市土地价格和住房价格持续上涨，导致城市劳动力生存黏性降低；另一方面房地产业高收益的特点会吸附大量资金向其聚集，对制造业发展产生排挤效应。在劳动力生存黏性下降和房地产业对制造业产生排挤效应的双重作用下，制造业呈现出从东部城市向中西部城市转移的特征。2022年1月14日，工业和信息化部、国家发展和改革委员会等十部门联合发布《关于促进制造业有序转移的指导意见》，要求到2025年，产业转移政策环境更加完善，中西部、东北地区承接产业转移能力显著提升，制造业布局进一步优化、区域协同显著增强1。

为此，理论界对城市住房价格、劳动力流动与制造业转移之间的内在逻辑关系进行了深入探讨，得出结论：城市住房价格上涨会降低劳动力相对效用，阻碍劳动力向城市流入，降低城市产业集聚度；与此同时，城市住房价格上涨会导致本城市产业向住房价相对较低的城市转移，致使产业呈现分散化格局。然而，住房价格、劳动力流动与制造业转移之间既存在集聚效应又存在抑制作用，可能存在复杂的非线性关系。换言之，大中城市一方面象征着良好的城市发展前景、匹配度高的就业机会以及更大的财富增长空间，同时还意味着更优质的基础设施和公共服务水平。城市发展初期相对较低的住房价格在一定程度上会吸引劳动力流入，由于劳动力流动与产业集聚高度相关，进而形成产业集聚效应。另一方面，人口集聚导致住房价格上涨，这使劳动力生活负担加重，在劳动者追求自身效用最大化情形下，高住房价格会增加生产生活成本，阻碍劳动力流入，导致相对就业规模缩减，进而诱发制造业转移。因此，基于非线性关系解释和分析住房价格、劳动力流动与制造业转移之间的内在机理，对于引导制造业合理有序转移，促进形成区域合理分工、联动发展的制造业发展格局有着重要意义。

二、 文献综述

国内外学者针对住房价格、劳动力流动与产业转移间关系的研究虽较为丰富，但大多仅限于线性关系研究。Krugman[1]和Baldwin[2]根据新经济地理学相关理论研究得出劳动力供给状况直接导致企业的集聚程度，即劳动力集聚会带来产业转移，进而形成产业集聚。国内学者研究聚焦住房价格、劳动力流动与产业转移之间的线性关系。高波等[3]基于拓展引入住房价格因素的新经济地理学标准模型，首次将住房价格、劳动力流动和产业转移三者结合进行研究，发现区域住房价格差异导致劳动力流动，从而引发产业转移。刘志伟[4]发现城市住房价格上涨挤出部分企业，形成产业梯度转移，致使城市低附加值第三产业向高附加值领域转型。邵挺等[5]研究指出长三角地区大型城市住房价格高速上涨导致制造业從高住房价格地区迁移至低住房价格地区，形成制造业分散化布局。谭锐等[6]研究发现由于大城市在基础设施水平、劳动力等方面集聚优势超过住房价格高速上涨的集聚不经济，制造业更可能选择城市内而非城市间转移。席艳玲等[7]发现相对住房价格与第二产业就业和产出呈倒“U”型关系，即过高的房价会对第二产业造成挤出效应，抑制其就业和产出。赵杨等[8]则认为城市房价升高会对第二产业就业人数造成挤入，对第三产业就业人数造成挤出。林永民等[9]研究发现房价与产业结构升级也存在正向促进与反向抑制作用，即房价与产业结构升级存在倒“U”型关系，并且房价的非理性上涨会成为产业结构升级的阻力。

综上可见，已有成果更多基于住房价格、劳动力流动与制造业转移的线性关系展开研究，仅有的基于三者非线性关系的研究成果，缺乏理论模型支撑。为此，本文基于“中心—外围”模型，建立住房价格、劳动力工资、贸易自由度等因素与劳动力间接效用的函数关系，揭示住房价格与制造业转移间非线性关系的内在机理。本文可能的边际贡献在于理论层面构建非线性理论模型，为住房价格与制造业转移间非线性关系提供理论支撑；现实层面运用面板门限模型对理论模型中非线性关系进行实证检验，并确定城市住房价格于非线性关系中的拐点，为识别城市自身制造业所处的发展阶段提供依据。

三、 理论模型及内在机理

模型假定某国存在两个经济区：地区1和地区2，两地区劳动力均可自由流动，且不考虑农业部门情况。两地区消费者（同样也是劳动者）具有相同偏好，并通过合理分配收入，消费不可贸易住房和可贸易工业品，以实现效用最大化。

1. 消费者“效用最大化”条件下的工业品和住房需求函数

由柯布-道格拉斯函数形式表示地区[i=]{1，2}消费者效用如下：

[Ui=CμiMC1-μiH] （1）

[CiM=∫s∈Ndisσ-1σdsσσ-1]

[PiM=∫s∈NPis1-σds11-σ]

[PiMCiM+PiHCiH=Yi=WiLi] （2）

[0<μ<1<σ]

式（1）（2）中，[Ui]、[CiM]、[CiH]分别表示地区[i]消费者效用及所消费的差异化工业品和住房数量，[di]（s）代表地区[i]消费者第[s]种工业品消费量。[PiM]、[PiH]对应地区[i]工业品价格和住房价格，[PiM]为Krugman提出的工业品价格指数，[Pi]（s）为地区[i]第[s]种工业品价格，[Yi]为地区[i]经济总收入，[Wi]、[Li]分别代表地区[i]劳动者工资收入及数量。[N=Ni+Nj]，是地区[i]和地区[j]工业品种类之和，[σ]为工业品品种间的替代弹性，[μ]为消费者在工业品上的支付份额。

基于消费者“效用最大化”得地区[i]消费者对工业品与住房需求分别为：

[CiM=μYiPiMCiH=1-μYiPiH] （3）

进一步求得地区[i]消费者对地区[i]生产第[s]种工业品需求及对地区[j]生产第[s]种工业品需求：

[diis=Piis-σPiM1-σμYi            i=1，2，  s?Ni] （4）

[djis=TPjis-σPiM1-σμYi            i，j=1，2， s?Nj， T>1] （5）

式（4）（5）中，[Piis]表示生产于地区[i]销售于地区[i]的第[s]种工业品价格；[Pjis]表示生产于地区[j]销售于地区[i]的第[s]种工业品价格。[T]为Samuelson[10]提出的冰山运输成本。

2. 基于企业“利润最大化”优化工业品价格指数

假定制造业企业使用[β]单位劳动力可变成本和[m]单位固定成本进行产品生产，则地区[i]生产[xs]单位产品的成本函数为：

[TCiS=γ+βxisωi] （6）

式（6）中，[γ]为[m]单位固定成本的资本报酬，[xis]为地区[i]企业生产第[s]种工业品产量，[ωi]为地区[i]劳动者工资。则地区[i]制造业企业利润函数如下：

[Πis=Piisdiis+Pijsdijs-βωidiis+Tdijs-γ] （7）

由利润最大化条件得均衡价格如下：

[Piis=σσ-1βωiPijs=σσ-1Tβωi] （8）

[Pjjs=σσ-1βωjPjis=σσ-1Tβωj] （9）

则[PiM]价格指数形式可变为：

[PiM=σσ-1βNiωi1-σ+NjTωj1-σ11-σ] （10）

3. 构造并化简区域间劳动力相对效用函数

由消费者效用最大化条件得消费者间接效用函数，并将式（10）代入可得：

[Ki=μμ1-μ1-μWiLiP1-μiHσσ-1βμNiωi1-σ+Nj?ωj1-σα] （11）

式（1）中，[α=μ1-σ] ，[?=T1-σ]，[?]表示贸易自由度，[0

[Kj=μμ1-μ1-μWjLjP1-μjHσσ-1βμNi?ωi1-σ+Njωj1-σα] （12）

根据长期均衡的区位选择条件可知，劳动力跨区域流动的决定因素为两区域间相对效用，构造相对效用函数如下：

[Qij=KiKj=WiLiWjLjPiHPjHμ-1NiNjωiωj1-σ+?NiNjωiωj1-σ?+1-α] （13）

取对数化简得：

[lnQij=lnWiWj+μ-1PiHPjH-12PiHPjH2-αln?+?-α1-?2?NiNj-1 ] （14）

4. 利用区位选择理论建立住房价格与制造业就业间非线性关系

由长期均衡区位选择理論可知，两地区劳动力效用水平相同即[Qij=1]；则式[14]可变为：

[α1-?2-??NiNj=lnWiWj+μ-1PiHPjH-12PiHPjH2-αln?-1] （15）

进一步化简可得相对住房价格与制造业相对就业规模间非线性关系：

[NiNj=?α1-?2-? lnWiWj-?μ-12α1-?2-?PiHPjH2+?μ-1α1-?2-?PiHPjH-?αln?α1-?2-?]

由于[α<0]，[μ-1<0]，[00]

同时根据新经济地理学的假定可知，两地区的相对就业与[Ni/Nj]间存在高度正相关。借鉴已有参考文献，用两地区的相对就业规模代理[Ni/Nj]，从而可得相对住房价格与相对就业规模存在倒“U”型的非线性关系。由模型得出其内在机理为在经济发展初期，具有区位优势和政策优势的地区率先发展具有比较优势的产业，如制造业，此时生产要素价格较低，制造业企业的利润空间较大，高额利润驱使企业向该地区集聚，同时吸引了劳动力。当劳动力这一可流动要素大量集聚时会造成不可流动要素住房的相对数量减少，进而导致相对住房价格上涨。此时劳动力主体会被迫做出自身效用最大化的选择，即劳动力要想选择消费多样化产品，就必须忍受大城市房价，否则就迁移到小城市，于是本文提出命题1。

命题1：在地区间相对工资水平、贸易运输成本等一定条件下，相对住房价格与制造业相对就业规模存在倒“U”型的非线性关系。

而住房价格通过作用于劳动力流动影响制造业转移，其内在作用机制为作为理性经济人的劳动者追求效用最大化行为。为此，本文引入“生存黏性”的概念，用于衡量劳动力对所居城市的依存度，并从侧面反映劳动力转移意愿，进而揭示以劳动力为载体的制造业转移内在动因。生存黏性越弱，劳动力对所居城市依存度越低，则劳动力转移意愿就越强，制造业相对就业规模下降。于是本文提出命题2。

命题2：以制造业劳动力年均工资收入与所在地区住房价格的比值来刻画劳动力“生存黏性”，其与制造业相对就业规模高度正相关。

四、 实证分析

1. 实证模型设定与变量定义

本文选用2002—2020年35个大中城市面板数据，依据Hansen[11]提出的面板门限模型进行实证分析。模型优点在于无需给定非线性方程形式，门槛值及其个数由样本内生决定，且可避免模型引入平方项可能造成的多重共线性问题。面板门限模型类别基于门限值个数可分为单一面板门限模型与多重面板门限模型。本文依次进行单一门限及双重门限效应的检验，其模型设定如下：

[Yit=μi+θ1Xit?Iqit≤γ+θ2Xit?Iqit>γ+βZit+εit] （16）

其中，[μi]为个体截距项，[Xit]为核心解释变量，[qit]为门限变量，[Zit]为一系列控制变量，系数[θ1]、[θ2]、[β]以及门限值[γ]均为待估计参数，[εit]为随机扰动项，[ I?]为示性函数其具体形式如下：

[Iqit≤γ=1    if  qit≤γ 0    if  qit>γ      Iqit>γ=0    if  qit≤γ 1    if  qit>γ] （17）

由于缺乏企业区位变动信息相关数据，现有学者大多研究相对产业转移，将产业转移定义为产业份额或就业人员份额变动。本文借鉴杨亚平等[12]、胡安俊等[13]、高波等[3]的做法，以制造业相对就业规模或相对产值份额的变动来刻画制造业转移。故在面板门限模型中，以相对就业规模为被解释变量，相对住房价格为核心解释变量和门限变量，控制变量以德国韦伯工业区位理论为基础，分为行业层面和城市层面，共9个变量，数据来源于《中国城市统计年鉴》《中国房地产统计年鉴》及各城市统计年鉴。具体变量及数据描述见表1、表2。制造业相对就业规模、城市相对住房价格计算方式依次为：

[rempi=empij≠iempjn-1=n-1empij≠iempj    rhpi=hpij≠ihpjn-1=n-1hpij≠ihpj] （18）

2. 门限效应检验及回归结果分析

首先通过LLC单位根检验方法对样本数据进行平稳性检验，所有变量均通过检验，然后运用面板门限模型进行实证分析，门限效应检验及回归分析结果见表3、表4。

根据表3门限效应检验结果可知，所设立面板门限模型中存在1个门限，门限值为1.8146，门限区间为（1.8146，1.9674），P值为0.0133，在5%水平下显著。在表4面板门限回归结果中，当核心解释变量相对住房价格（Rhp）未达到门限值1.8146时，其系数估计值为0.1567，而达到门限值后为-0.3464，说明较低住房价格吸引制造业劳动力流入，增加城市制造业就业规模，从而促进制造业集聚效应的产生。但随着住房价格持续上涨，高住房价格带来的集聚不经济作用渐渐显现，劳动力相对效用水平会随着住房价格上升而降低，进而出现大量劳动力迁移，促使以劳动力为载体的城市制造业进行转移，即命题1成立。

此外，由式（22）测算可得2016—2020年北京、上海、广州、深圳的相对住房价格均值依次为2.734、2.224、1.947、4.1371，均超过门限值1.8146；其余城市均未超过门限值。这说明对于北上广深等一线城市而言，高住房价格对制造业就业规模产生负向影响，致使制造业集聚水平受到抑制，亟待通过制造业转移和升级促进经济可持续增长；而其余大中城市在其相对住房价格达到门限值前将继续享受较低住房价格带来的劳动力福利，进而提升自身制造业集聚水平，其同时也是承接一线城市制造业转移的主要力量。

而从制造业层面控制变量看，制造业基础设施水平（LnFa）及劳动生产率（LnLp）变量的系数估计值分别为0.1669、-0.0857，均在1%水平下显著。表明制造业基础设施水平对制造业就业规模具有正向影响，即制造业基础设施水平的提高在一定程度上促进制造业就业规模扩增，进而提高制造业集聚水平。劳动生产率系数显著为负，则说明随着劳动生产率的提高，制造业相对就业规模降低，主要因为制造业技术发展水平越高，其自动化水平越高，进而劳动力需求大量降低。对于城市层面控制变量而言，城市集聚效应（LnPd）、金融发展水平（LnTdl）及贸易自由度（LnTrans）等变量的系数估计值均在1%水平下显著，教育条件（LnEdu）在5%水平下显著，表明城市人口集聚、较高的金融发展水平和贸易水平以及良好的医疗卫生条件均能促进劳动力聚集，进而提升城市制造业集聚水平。

3. 内生性问题

所设定模型经Hausman检验可知，拒绝“所有变量均外生”的原假设。并且从逻辑关系看，城市相对住房价格与相对就业规模或相对产业份额间可能存在由反向因果导致的内生性问题。产业份额较高或就业规模较大，城市一般要素禀赋水平较高，同时又因大城市“虹吸效应”而造成人口与资金集聚现象，进一步推高住房价格。本文选用工具变量法中两阶段最小二乘法估计（2SLS），以便有效解决模型内生性。余泳泽等[14]、陈斌开等[15]的研究指出在中国国情下，土地供应状况是影响城市房价的重要直接因素。本文借鉴陈斌开等[15]做法，以省级人均土地购置面积与滞后一期住房价格为当期城市住房价格的工具变量，数据来源于《中国房地产统计年鉴》。OLS、个体固定效应及2SLS估计结果见表5。

由表5回归结果可知，在引入工具变量的2SLS估计中，除了代表城市贸易自由度的变量外，其余变量均在不同水平下显著，且模型拟合程度较好。此外，制造业劳动力成本的系数显著为正，表明较高的工资水平会吸引劳动力流入，从而增加制造业相对就业规模，促进制造业集聚发展；城市教育水平和医疗卫生条件变量的系数显著为正，表明教育资源和医疗卫生水平均为吸引制造业劳动力流入的关键因素，随着教育、医疗等公共服务的供给水平提高，制造业相对就业规模扩增。OLS、个体固定效应和2SLS模型的核心解释变量相对住房价格系数为正，平方项系数为负，与理论模型推导结果保持一致，且2SLS估计中相对住房价格及其平方项均在1%水平下显著，则命题1成立。

4. “生存黏性”檢验

对于命题2，本文以制造业工人年均工资收入与所在地区住房价格比值刻画生存黏性，即变量Se。生存黏性用于衡量劳动力对所居城市依存度，生存黏性越强即劳动力年均工资收入与住房价格比值越高，劳动力依存度越高，则劳动力转移意愿就越弱，更有利于城市吸引并留住劳动力。将生存黏性（Se）作为核心解释变量纳入OLS模型和面板个体时点双固定效应模型进行分析，为避免多重共线性，剔除变量Rw，回归结果见表6，由于篇幅限制，故不显示控制变量。

由表6可知，各模型核心解释变量生存黏性（Se）与制造业相对就业规模（Remp）显著正相关。在面板个体时点双固定效应模型中，生存黏性的系数为0.0341，在1%水平下显著，即劳动力的生存黏性每提高1个单位，制造业相对就业规模增加约0.034个单位。这表明随着劳动力生存黏性增强，劳动力对所居城市依存度提高，有利于城市吸引并留住外来劳动力，扩大制造业就业规模，进而推进自身制造业集聚发展，则命题2成立。

5. 稳健性检验

为得到住房价格与制造业转移间非线性关系较为完整的分析，本文采用系统广义矩估计（SYS-GMM）进行稳健性检验，引入工具变量（省级人均土地购置面积、滞后一期住房价格）后的估计结果如表7所示，由于篇幅限制，故不显示控制变量。

根据SYS-GMM模型估计结果可知，相对住房价格及其平方项的系数均高度显著且平方项为负，意味着相对住房价格与制造业的相对就业规模呈倒“U”型关系，说明较低的住房价格吸引制造业劳动力流入，促进制造业集聚，然而随着住房价格不断拉升至一定程度时，更高的住房价格意味着更高的生活成本，高房价的抑制作用开始显现，制造业的相对就业规模出现缩减，再次验证命题1中的非线性关系。同时根据模型的回归系数计算相对住房价格的拐点为1.965，与2SLS模型中相对住房价格拐点2.1755的差异较小，即相对住房价格为1.965时，制造业相对就业规模达到倒“U”曲线的拐点。其余各变量除城市教育条件外，均在不同水平下显著，且模型系数估计与上文基本保持一致。

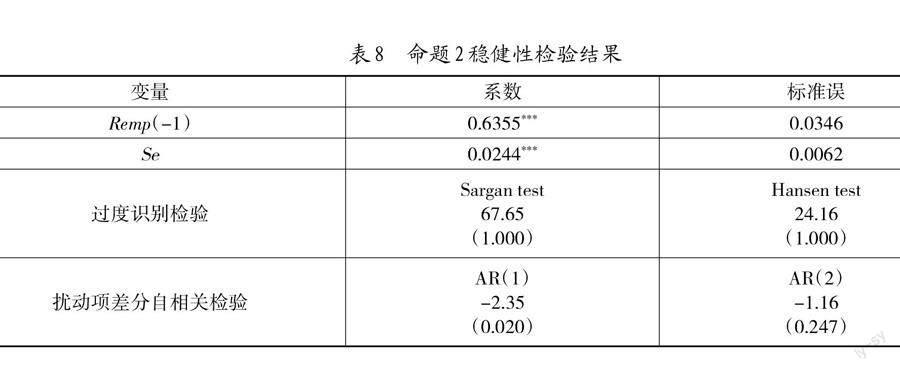
考虑到生存黏性（Se）与制造业相对就业规模（Remp）之间存在一定互动关联性，为有效避免内生性带来的偏误，本文同样采用SYS-GMM估计对命题2进行稳健性检验。由表8可知，生存黏性与制造业相对就业规模成显著正相关，随着劳动力的生存黏性提高，其对所居依存度越高，则劳动力转移意愿就越弱，同时也更吸引外来劳动力，进而制造业相对就业规模不断扩增。城市医疗卫生条件（LnHealth）、教育条件（LnEdu）的估计系数不显著，这可能是因为部分大中城市的教育资源和医疗卫生水平均相对落后，无法充分发挥教育医疗等公共服务吸引人才的作用。

五、 结论与建议

1. 结论

实证结果表明：（1）在控制行业层面和城市层面等变量情形下，城市相对住房价格与制造业相对就业规模存在倒“U”型的非线性关系。相对较低的住房价格吸引外来劳动力流入，增加城市制造业就业规模，提升自身制造业集聚水平。但随着外来人口流入，住房需求不断增加，大量需求助推住房价格上升，致使住房价格持续走高。城市劳动力因负担不起高昂住房成本而被迫迁出，导致制造业就业规模下降，进而引起城市部分制造业转移，加大制造业“空心化”风险。（2）以制造业劳动力年均工资收入与所居城市住房价格的比值刻画的生存黏性与城市制造业相对就业规模显著正相关，揭示了以劳动力为载体的制造业转移内在动因。劳动力流动由其生存黏性强弱决定。非一线城市的住房价格相对较低，劳动力对所居城市的依存度高，生存黏性较强，且更容易吸引外来劳动力流入，进而提高了自身制造业集聚水平。对北上广深一线城市而言，部分劳动力收入与支出严重不匹配导致其生存黏性较弱，从而出现以“用工荒”为内在动因的制造业转移。

2. 建议

（1）优化资源配置，合理调控城市住房价格，防止制造业“空心化”。相较于地价、刚性需求等因素，教育、医疗、金融等资源的不合理分配才是区域房价差异化的深层次原因。东部发达地区应当结合经济手段和行政手段，合理调控因资源配置不合理导致的虚高住房价格，防止因虚高住房价格而出现制造业“空心化”现象。中西部地区应当牢固把握较低住房价格的优势，优化公共服务资源与基础设施，吸引并留住外来劳动力，在促进自身制造业集聚水平的同时做好承接东部地区制造业转移的充分准备。

（2）“因城施策”，制定科学合理的住房政策以满足劳动力流动与自身制造业高质量发展的要求。对于东部发达地区来说，其首要任务是制定吸引和留住高技能劳动力的住房政策，比如住房补贴、税收减免等，形成满足制造业转型升级要求的人才储备。中西部地区应健全多层次住房保障体系，大力发展公共租赁住房，以满足外来劳动力流入的住房需求，在做好承接制造业转移充分准备的同时，为自身制造业转型升级保留充足发展空间。

（3）实施区域制造业差异化发展战略，合理引导制造业梯度转移。各地区应立足于自身比较优势，从制造业发展的实际出发，制定并实施制造业转移与协调发展的行业规划，明确其行业价值链所处位置，合理引导制造业自发梯度转移，真正实现区域优势互补与协同发展。

参考文献：

[1] Krugman P.Increasing Returns and Economic Geography[J].Journal of Political Economy， 1991，99（3）：483-499.

[2] Baldwin R， Forsild R， Martin P， et al.Economic Geography and Public Policy[M].Princeton：Princeton University Press，2011.

[3] 高波，陈建，邹琳华.区域房价差异、劳动力流动与产业升级[J].经济研究，2012，47（1）：66-79.

[4] 劉志伟.城市房价、劳动力流动与第三产业发展——基于全国性面板数据的实证分析[J].经济问题， 2013（8）：44-47.

[5] 邵挺，范剑勇.房价水平与制造业的区位分布——基于长三角的实证研究[J].中国工业经济，2010（10）：24-32.

[6] 谭锐，赵祥，黄亮雄.高房价下的制造业转移：城市间还是城市内？[J].经济学报，2015，2（2）：56-75.

[7] 席艳玲，吉生保，王小艳.要素相对价格对产业结构调整的倒逼效应分析——基于省际动态面板数据的系统GMM估计[J].财贸研究，2013，24（5）：18-24.

[8] 赵杨，仲崇文.新型城镇化建设下不同类型就业人口流动的影响因素研究——基于房价波动的视角[J].经济纵横，2021（8）：50-60.

[9] 林永民，吕萍.房价差异影响产业结构高级化的机理研究——基于核心—边缘模型的分析框架[J].现代管理科学，2017（12）：24-26.

[10] Samuelson P A.The Transfer Problem and Transport Costs： the Terms of Trade When Impediments are Absent[J].The Economic Journal，1952，62（246）：278-304.

[11] Hansen B E.Testing for Structural Change in Conditional Models[J].Journal of Econometrics，2000，97（1）：93-115.

[12] 楊亚平，周泳宏.成本上升、产业转移与结构升级——基于全国大中城市的实证研究[J].中国工业经济，2013（7）：147-159.

[13] 胡安俊，孙久文.中国制造业转移的机制、次序与空间模式[J].经济学季刊，2014，13（4）：1533-1556.

[14] 余泳泽，张少辉.城市房价、限购政策与技术创新[J].中国工业经济，2017（6）：98-116.

[15] 陈斌开，黄少安，欧阳涤非.房地产价格上涨能推动经济增长吗？[J].经济学季刊，2018，17（3）：1079-1102.

基金项目：国家社会科学基金一般项目“中国产能过剩测度、周期波动与供给侧结构性改革化解研究”（项目编号：16BYJ011）。

作者简介：杨立勋（1965-），男，西北师范大学经济学院教授，硕士生导师，研究方向为宏观经济统计分析；张志强（1998-），男，西北师范大学经济学院硕士研究生，研究方向为宏观经济统计分析；陈凯达（1997-），男，西北师范大学经济学院硕士研究生，研究方向为宏观经济统计分析。

（收稿日期：2022-09-27  责任编辑：殷 俊）