Photometric Monitoring of Blazar 3C 66A with the Yunnan University Astronomical Observatory 1m Telescope
Wei Zeng , Tao Wen, Zhen-Lu Gong, Shi Chen, Fan Wu, Hao-Yang Zhang, and Ben-Zhong Dai
1 School of Physics & Astronomy, Yunnan University, Kunming 650091, China; zengwei@ynu.edu.cn, bzhdai@ynu.edu.cn
2 Key Laboratory of Astroparticle Physics, Yunnan Province, Kunming 650091, China
3 Astronomical Observatory, Yunnan University, Kunming 650500, China
Abstract 3C 66A is one of our first batches of photometric monitoring objects with the 1 m optical telescope at Yunnan University Astronomical Observatory.In the present work,the observational campaign was performed from 2021 November 1 to 2022 February 27 in the Johnson–Morgan system V and R bands.The average magnitudes in each band were V = 15.52 ±0.18 mag and R = 15.07 ±0.17 mag.The overall variability amplitudes were ΔV=0 74, Amp=70.27% and ΔR=0 72, Amp=68.56%, respectively.Most of the intraday variabilities(IDVs) occurred in 2021 December and 2022 February.The minimal rise/decay timescale was about 6 minutes(5.82±2.74 minutes and 6.18±2.81 minutes on 2022 February 11,6.99±3.70 minutes and 6.17±2.91 minutes on 2022 February 12).Durations of these rapid variabilities were from 11.99 to 179.67 minutes.The discrete correlation function analyses between V and R bands showed significantly correlated variability.Color index analysis of IDVs showed that the spectrums do not change with variabilities.
Key words: (galaxies:) BL Lacertae objects: individual (3C 66A) – galaxies: photometry – galaxies: active
1.Introduction
3C 66A (or0219+428;α=02:22:39.6114,δ = +43:02:07.799, J2000) is one of the most luminous blazars at TeV γ-rays,which is a BL Lac type object classified as an intermediate synchrotron peaked blazar(Ackermann et al.2015) at redshift z=0.444 (Miller & McGimsey 1978) by detected Mg II emission line, or z=0.340 by detected host galaxy (Torres-Zafra et al.2016)).It was detected at VHE γrays (very high energy, VHE; E >100 GeV) by the Very Energetic Radiation Imaging Telescope Array System (VERITAS,Acciari et al.2009)and the Major Atmospheric Gamma Imaging Cherenkov Telescopes(MAGIC,Aleksić et al.2011).
In optical bands, the 1.56 m telescope of the Shanghai Astronomical Observatory (ShAO) had been monitored from 1996 December 11 to 2009 December 28(Fan et al.2018).The GLAST-AGILE Support Program (GASP) of the Whole Earth Blazar Telescope (WEBT) carried out multiwavelength monitoring in 2003–2004 (Böttcher et al.2005) and 2007–2008(Böttcher et al.2009).The Steward Observatory of the University of Arizona in support of the Fermi γ-ray observations (Smith et al.2009) contributed optical data from years 2008 to 2018.Using an extremely wide field of view camera,the Zwicky Transient Facility (ZTF) (Bellm et al.2019; Masci et al.2019)scanning the entire Northern sky from 2018 March also carried out the optical monitoring of 3C 66A in ZTF_g,ZTF_r, and ZTF_i bands.
Combining the above-mentioned sky survey data and additional observational data, 3C 66A intra-day variability(IDV) has been widely addressed by several authors with timescales ranging from 14.5 to 344.0 minutes (Gupta et al.2012; Kaur et al.2017; Fan et al.2018; Pasierb et al.2020).This source also exhibited quasi-periodic variability.Lainela et al.(1999) investigated a period of 65 days, similar to~50–57 days by Böttcher et al.(2005), while different longterm analyses claimed periods of 156 days, ~2 yr (Fan et al.2018),~2.3 yr(Cheng et al.2022),~2.5 yr(Kaur et al.2017),and ~3 yr (Otero-Santos et al.2020; Cheng et al.2022).
Blazars are characterized by non-thermal emission, strong and rapid variability, and corresponding timescales extending from a few minutes to years and even decades.So photometric monitoring is a powerful tool to study the structure and radiation mechanism of blazars by measuring their variability amplitude,periodic or aperiodic timescales,and color behavior.In this work, we performed optical monitoring of 3C 66A to study its flux and color variability on short-term timescales.In Section 2,we will describe the observations and data reduction procedures.Section 3 presents the results.Our discussions and conclusions are given in Section 4.
2.Observations

Figure 1.Contour map of YNUAO location.The observatory is located on the top of Yunshan Mountain,with an altitude of 2009.5 m.The upper right corner is the layout of the Chenggong Campus of Yunnan University.
The one-meter ALT-AZ Ritchey Chret́ien Telescope at Yunnan University Astronomical Observatory (hereafter,YNUAO) was officially operational on 2021 December 27.It is operated by Department of Astronomy, Yunnan University.This is a Ritchey–Chretien telescope made by APM-Telescopes GmbH in Germany,equipped with Andor’s iKon-XL 231 CCD camera platform.
2.1.Site Conditions
The location of the YNUAO is 102° 51′ 02″ (E),2 4°4 9 ′1 2″(N),with an altitude of 2009.5 m (Figure 1).Figure 2 shows the data recorded from 2017 March 23 to April 13 to evaluate the site seeing conditions of YNUAO.
2.2.1-meter Telescope and CCD Characteristics
The one-meter telescope at YNUAO (YNUAO-1m) has a Ritchey ́
Chretien design with an effective system focal ratio of f/8 by LOMO Optic Set.It has a hyperbolic primary mirror with an effective diameter of 1005 mm(1019.4 mm mechanical diameter), and a hyperbolic secondary mirror with an effective diameter of 369 mm (375 mm mechanical diameter).Two Nasmyth focal stages with image de-rotators are switched through the tunable tertiary mirror.The images have 80%encircled energy (EE80) of 0 5 maximum, over the entire corrected field of view.The telescope has been optimized for the wavelength range of 350–900 nm with a reflectance of at least 85%on each mirror.The baseline for the telescope mirror coatings (for primary, secondary, and tertiary mirrors) is aluminum with protection.The blind pointing accuracy is less than 10″rms (i.e., open-loop).Tracking accuracy and field derotation compensation will not degrade images at the periphery of the field of view by more than 1 0 rms over a minimum period of 1000 s.Figure 3 shows the distribution of displacement deviation of 1000 s of continuous exposure image over time (single 10 s exposure, 100 consecutive frames).The accuracy can reach 0 72 rms for open-loop tracking.
The iKon-XL 231 CCD camera is used for photometry for YNUAO-1 m.It is a thermoelectrically(TE)cooled,very large area CCD camera platform with the e2v CCD231-84 Astro back-illuminated sensor, offering a very large 61.4×61.4 mm imaging area from a 4096×4108 array format and 15 μm pixel size.The minimum temperature achieved for the TE cooler is set to-100°C with water/liquid cooling.For a standard silicon sensor with mid-band AR coating, peak quantum efficiency could be larger than 95%.The high sensitivity model offers the absolute best CCD performance available, combining exceptionally low read noise of 2.2 electrons with a very large well depth of 350,000 electrons (in system readout rate 100KHz 18 bit).The minimum dark current achievable is 0.0002 electrons pixel-1second-1(@ sensor temperature of -100°C with 16°C water cooling).
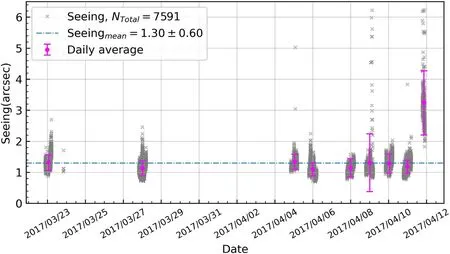
Figure 2.The curve of seeing at Chenggong Campus of Yunnan University from 2017 March 23 to April 12.

Figure 3.The distribution of displacement deviation of 1000 s continuous exposure image(single 10 s exposure,100 consecutive frames).The left panel is open-loop tracking, and the right panel is closed-loop tracking.
2.3.Data Reduction
Our monitoring of 3C 66A with the YNUAO-1 m was from 2021 November 1 to 2022 February 27 in Johnson–Morgan system V and R bands in the alternate mode.The typical exposure times for V and R bands are 120 s and 80 s respectively.A total of 42 observation nights and 2533 CCD frames (including 1280 in the V band and 1253 in the R band) were obtained.All images were still reduced with the standard image reduction and analysis facility (IRAF).4IRAF is the Image Reduction and Analysis Facility, a general purpose software system for the reduction and analysis of astronomical data.IRAF was written by the National Optical Astronomy Observatories (NOAO) in Tucson,Arizona.However, development and maintenance of IRAF is discontinued since 2013 October.The iraf-community is still working on integrating the available patches into the IRAF source code and fixing bugs.Aperture photometry radii of the source and comparison stars are performed with the same value in each frame,which is determined by the FWHM of the source.As in our previous work, we concentrate on an aperture radius of about 1.5 FWHM for our analysis, which always provides the best signal-to-noise ratio(S/N)(Zeng et al.2017,2018,2019).We used the three comparison stars,star“2,”star“3”and star “5”listed in Table 1, to obtain magnitudes for 3C 66A, and then calculated the average and corresponding standard deviation as the magnitude of 3C 66A in each photometric observation.According to the deviation of the average of the differential instrumental magnitude of comparison stars “2”and “5,”Δ(star 2-star 5), we estimated the uncertainty in our observation campaign to be ±0.05 mag.Figure 4 shows the distribution of uncertainty in our observation in each band for the entire observational campaign.
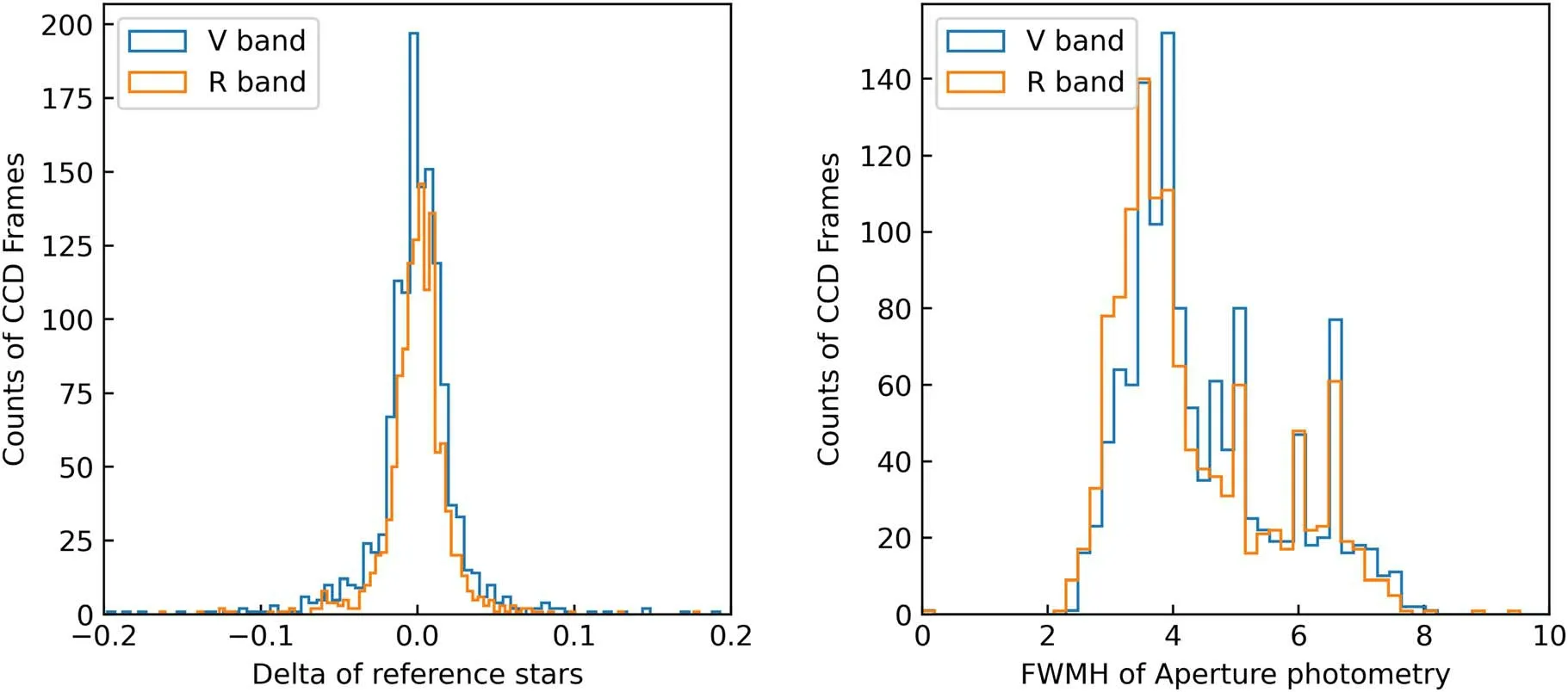
Figure 4.Distribution of uncertainty in our observation in each band for the entire observational campaign.The left panel is the distribution of the deviation of the differential instrumental magnitudes of comparison stars 2 and 5 in bands V and R.The right panel is the distribution of full width at half-maximum (FWHM) of 3C 66A for each observation.

Table 1 The Magnitudes of the Comparison Stars
3.Results
3.1.Variability


We used a variability parameter C, generalized by Romero et al.(1999), as

Figure 5.Light curves from 2021 November 1 to 2022 February 27 in V and R bands.

Table 2 Results of the Timescale Analysis are Shown in Figure 6
where σSource-Star2, σSource-Star5, and σStar2-Star5are standard deviations of the differential instrumental magnitudes of 3C 66A and comparison star 2, 3C 66A and comparison star 5, and comparison stars 2 and 5, respectively.
The χ2test is also used,

To investigate thepresence ofvariability,theFtest(and χ2test) was comparedwith the Fα,ν(and)critical value,where ν is the degrees of freedom and α is the significance level.In this paper,both the F test and χ2test were performed at two significance levels: 0.99 and 0.999.As described by Romero et al.(1999), if C >2.576, then the source was classified as a variable at significance levels: 0.99.We considered an IDV to have occurred (variable, V), if the statistics from both tests were satisfied at the 0.999 level (or C >2.576).None of the criteria was met at the 0.99 level (or C <2.576): it was marked as non-variable (NV), nor was it marked as a probable variable (PV).The results of the F-test,C-test, χ2-test, and the IDV observations in V and R bands are presented in Table A1.

Figure 6.Light curves of 3C 66A with flux in units of mJy and time in units of JD-JDstart.The red lines are the best fitting by an asymmetric flare template and the corresponding gray areas are 3σ confidence intervals.
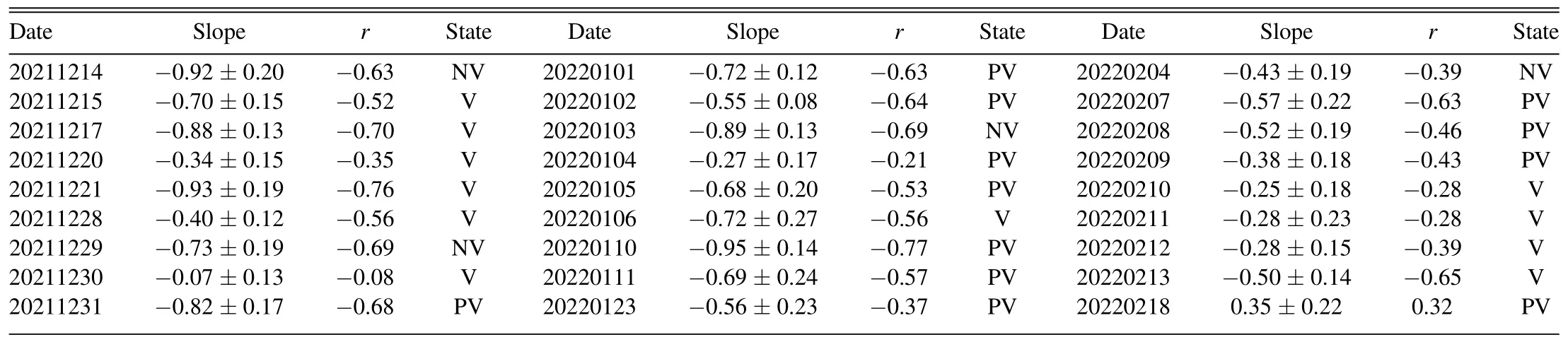
Table 3 Color Variability Epochs and Fit Parameters of Figures 11, 12, and 13
During the 42 observation nights, two light curves were marked as “V”in the V band, while 12 were in the R band.Among the 12 nights IDV occurred,2021 December accounted for 6, and 2022 February accounted for 4.Some of the IDVs showed monotonically increasing or decreasing trends during observations.While for others shown flares, we fitted them with an asymmetric flare template (Danforth et al.2013):
where Tr,imeans rise timescales and Td,imeans decay timescales.The results of the light curves are shown in Figure 6 and Table 2.The reliable minimal rise/decay timescale is about 6 minutes, while the durations of variations can last 12 minutes or more.
3.2.Cross-Correlation Analysis
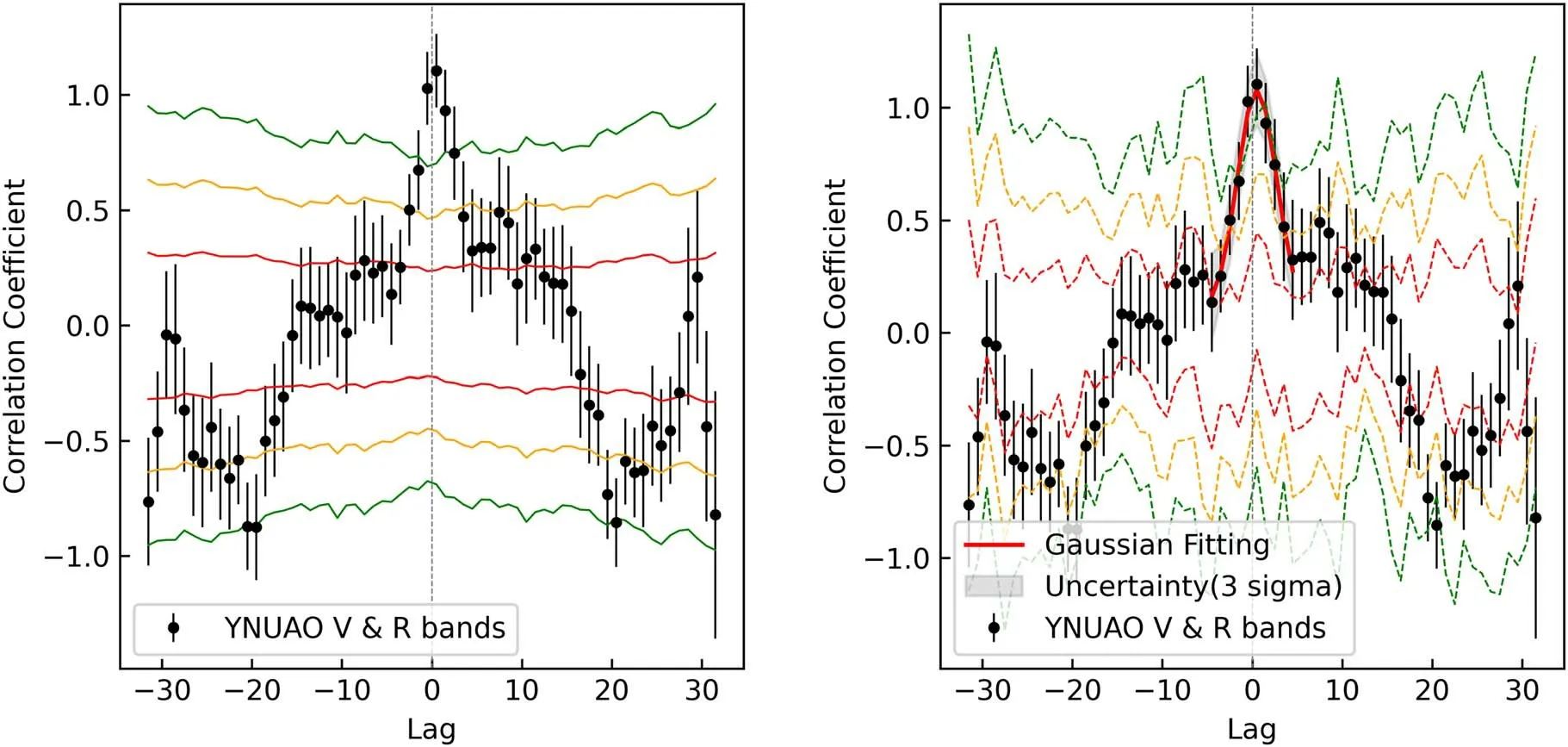
Figure 7.The DCFs between the V and R bands in daily average magnitudes,the time lag was τcent=0.52±0.08 day.The dots represent the cross-correlation for the data,while the color lines show the distribution of random cross-correlations obtained by the Monte Carlo method with 1σ(red),2σ(orange),and 3σ(green).The left panel shows uncertainties with Model-dependent Monte Carlo Method and the right panel with Model-independent.
In the variability analysis, we found that the light curves in the V and R bands showed consistency of variability, so we carried out the discrete correlation function (DCF) (Edelson &Krolik 1988) to analyze the correlation between the V and R bands with uncorrected light curves.While there is no general agreement on how to estimate the confidence levels (or significant levels) in DCFs, probably the method that has the widest acceptance is Monte Carlo (MC) simulations.For Model-dependent Monte Carlo Method, confidence is estimated by generating multiple randomized versions of time series with the same statistical properties (a simple power-law power spectral density, PSD ∝ν-α, α ≈2.0±0.5) and rerunning the DCF.All simulated time series are generated by a power law noise algorithm (Timmer & Koenig 1995), which randomizes both the amplitude and phase of the Fourier transform coefficients consistent with the statistical properties of the periodogram.Each simulated time series applied the same sampling,interpolated into the same time grid,and added corresponding errors.The distribution of DCFs of these simulated light curves is used to estimate the confidence levels of the data DCF (Max-Moerbeck et al.2014; Jackman et al.2018).
The determination of a model responding to discrete time series is similarly fraught with uncertainty because the origin of irregular continuum variations is unknown, which leads to the uncertainty of the index α and simulated light curve model.Therefore,methods by which the uncertainties in DCFs can be estimated in a less model-dependent fashion that is simple to implement.
In our photometric monitoring program, uncertainties in measured fluxes can be a significant source of error.The uncertainties in our observation campaign are normally distributed (as shown in Figure 4 left panel).We thus modify each flux by random Gaussian deviation based on the quoted error for each datum, which is regarded as “flux randomization”(FR).Cross-correlation results can be highly sensitive to the dispersion of data resulting from non-continuously sampled light curves and different time resolutions (exposure times).Thus, random subset selection (RSS) based on a randomly chosen subset of the original data points is implemented.Each MC realization is based on a number of data points that is typically 37% (1/e ≈0.37, Poisson probability) smaller than the real data set.The two elements can be combined in a single MC realization as Monte Carlo “FR/RSS”(Peterson et al.1998, 2004) method.
We took 103MC simulations for both methods, shown in Figures 7, 8, and 9, the color lines show the 1σ (red), 2σ(orange), and 3σ (green) uncertainties.Then we fitted DCFs with a Gaussian function as: DCF (τ) =Ae-(τ-τcent)2(2σ2).Generally, the centroid of the DCF τcentis recommended as the lag rather than the location of the peak τpeak.During our observation campaign, variation in V and R bands showed a correlation, and time lag was τcent=0.52±0.08 day for daily average magnitudes and τcent=0.12±0.08 day for all observation frames.From this comparison, it can be found that in the optical V and R bands, the 3C 66A had an intra-day delay timescale.For 2021 December, the time lag was τcent=(5.35±1.02)×10-3day (7.70±1.47 minutes).While in 2022 February, it was τcent=(-3.60±0.43)×10-3day(-5.18±0.16 minutes).As time resolutions were ~3.90 minutes between V and R bands, these time lags were acceptable.
3.3.The Spectral Properties

Figure 8.The DCF between the V and R bands, the time lag was τcent=0.12±0.08 day.The dots represent the cross-correlation for all data, while the color lines show the distribution of random cross-correlations obtained by the Monte Carlo method with 1σ (red), 2σ (orange), and 3σ (green).
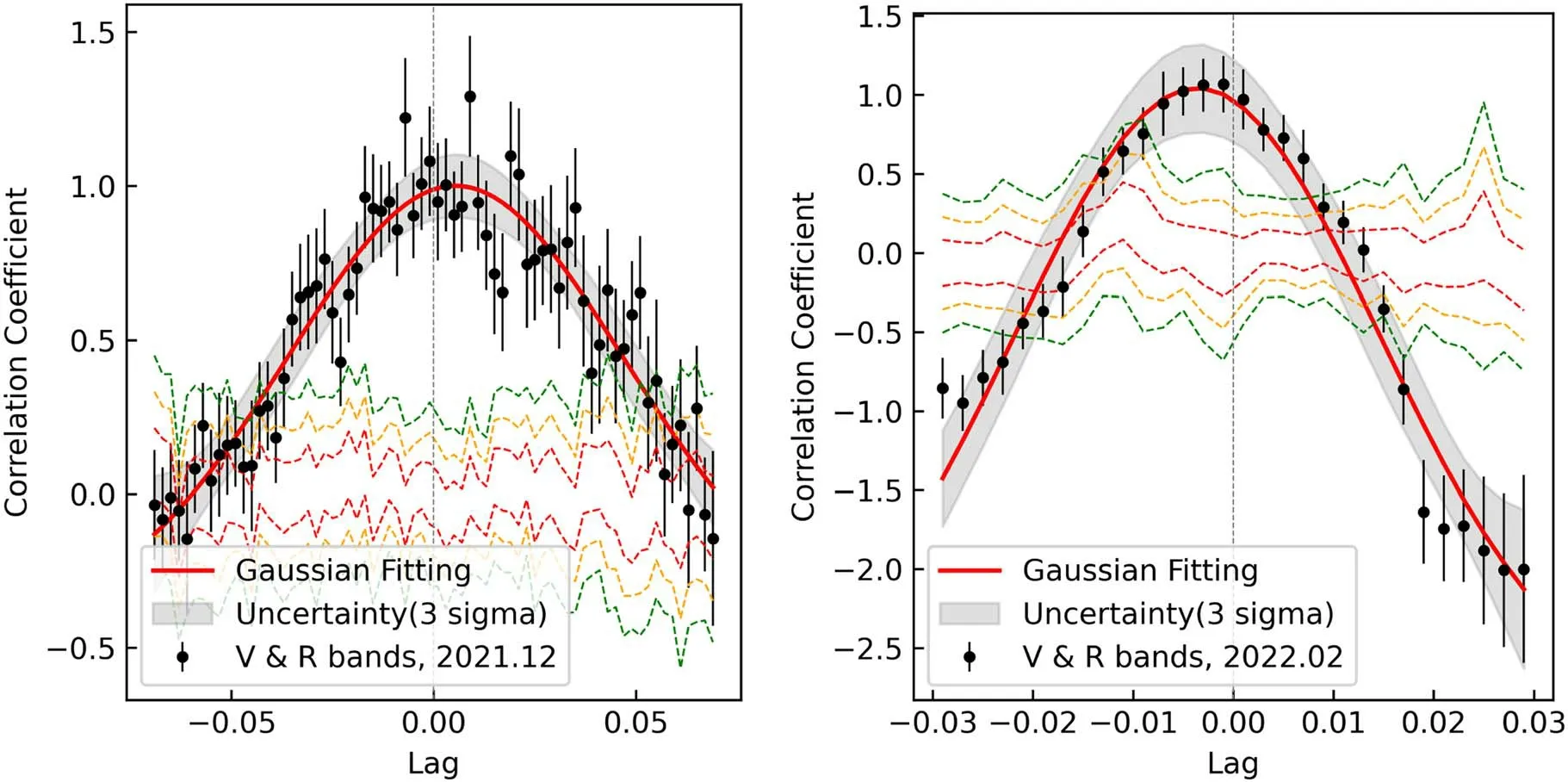
Figure 9.The DCFs between the V and R bands.The left panel is from 2021 December,the time lag was τcent=(5.35±1.02)×10-3 day,and the right panel is from 2022 February, the time lag was τcent=(-3.60±0.43)×10-3 days.
DCF analysis indicated that 3C 66A should have consistent spectral behavior during variability.Here we considered variations in the color indices V-R of 3C 66A with respect to variations in its brightness in the R band in 2021 December and 2022 February (as shown in Figure 10).Analysis of these two time periods showed that a weak positive correlation between the color index and brightness, with a slope of-0.40±0.05, r = -0.40 for 2021 December, and a slope of-0.16±0.05, r = -0.19 for 2022 February.The color bar represents the progression of time of color index variability with brightness, in units of Julian Day and from observation start time.Figures 11, 12, and 13 show the color–magnitude correlation for individual nights in consecutive months.Table 3 lists the slope and correlation coefficient for each color variability diagram.The intra-day analysis results showed that,in most cases, there was a negative correlation between the color index and the magnitude.However, the strength of this correlation had nothing to do with whether the variability occurred.Irregular minor variations in timescales of days superimposed on long-term trends led to a weak negative correlation between the color index and magnitude.

Figure 10.Optical color index vs.magnitude plots of 3C 66A in 2021 December and 2022 February.The color bars indicate the progression of time in units of JD-JDstart.

Figure 11.Optical color index vs.magnitude plots of 3C 66A in 2021 December.The color bars indicate the progression of time in units of JD-JDstart.
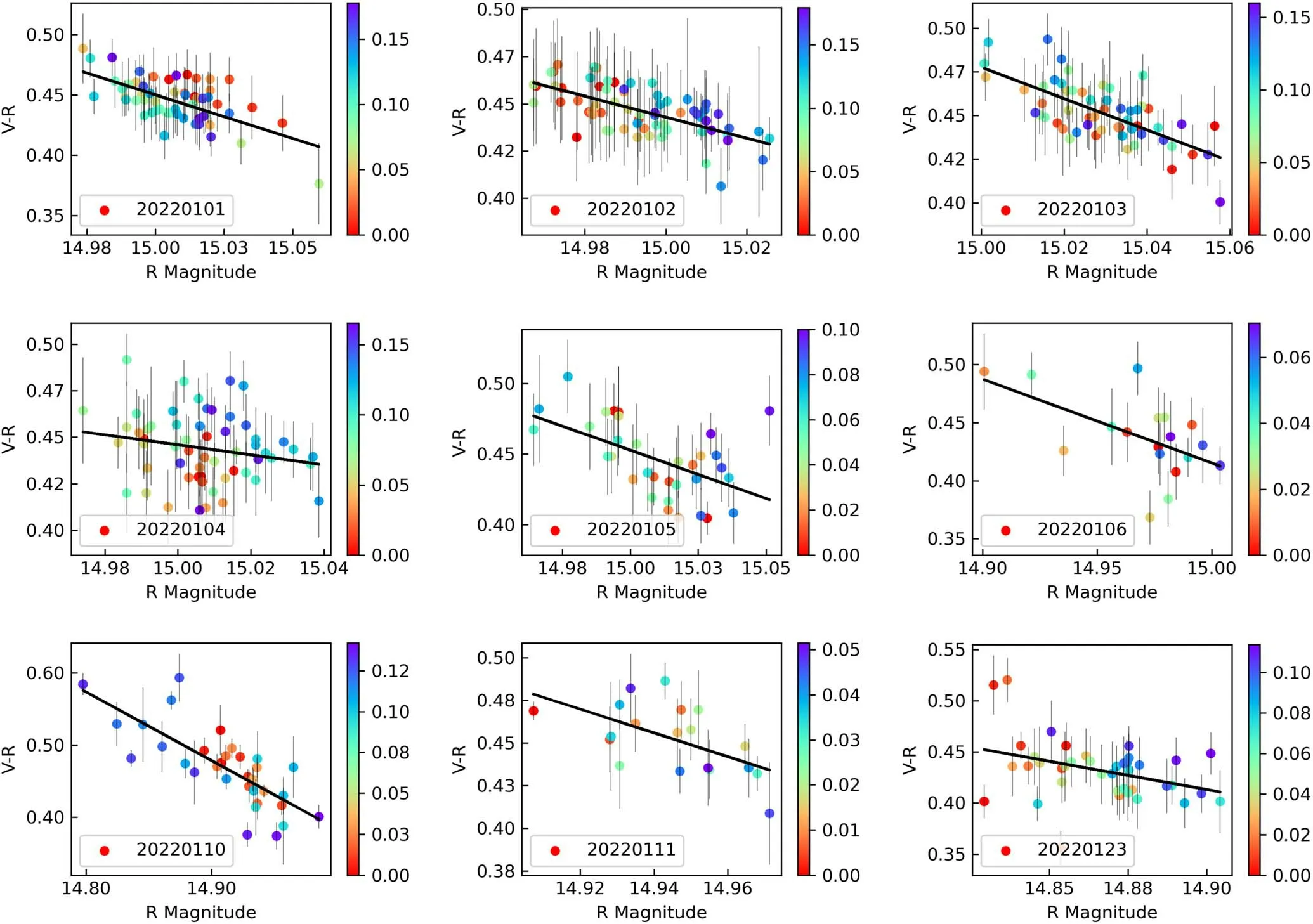
Figure 12.Optical color index vs.magnitude plots of 3C 66A in January 2022.The color bars indicate the progression of time in units of JD-JDstart.
4.Discussions and Conclusions
3C 66A has been observed intensively in the optical band(Lainela et al.1999;Böttcher et al.2005,2009;Tao et al.2011;Gupta et al.2012; Kaur et al.2017; Fan et al.2018; Otero-Santos et al.2020;Pasierb et al.2020 and references therein).It is also one of our first batches of photometric monitoring objects with the 1 m optical telescope at Yunnan University Astronomical Observatory (YNUAO-1m).Our observational campaign was performed from 2021 November 1 to 2022 February 27 in the Johnson–Morgan system V and R bands.The average magnitudes in each band wereV= 15.52 ±0.18 mag andR= 15.07 ±0.17 mag.Corresponding variability amplitude in each band was respectively ΔV=0 74,Amp=70.27% and ΔR=0 72, Amp=68.56%, while distribution of Amp was around AmpV,median~10.32% and AmpR,median~9.63%(shown in Figure 14).During this period,3C 66A showed active states twice: 2021 December and 2022 February.The flux showed a continuous increasing or decreasing trend during the observation nights, which meant most intraday light curves showed monotonic variations(shown in Figure 15) with timescales greater than the observational duration.Combined with the minimal rise/decay timescale (shown in Figure 6 and Table 2), the durations of variations were ΔT ⋍11.99-179.67 minutes.These timescales were consistent with the results of ΔT=23.18-344.02 minutes(with Amp=13.2%–92.8%)by Fan et al.(2018)and ΔT=10–32 minutes (with ΔB=0 52–0 46) by Xie et al.(1992).
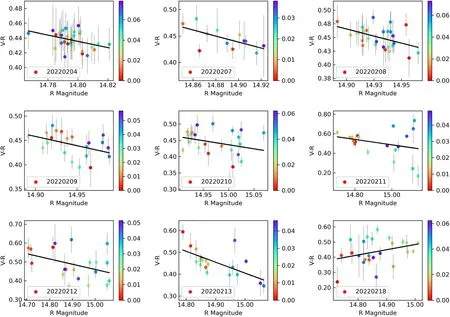
Figure 13.Optical color index vs.magnitude plots of 3C 66A in 2022 February.The color bars indicate the progression of time in units of JD-JDstart.

Figure 14.Distribution of the variability amplitude(Amp)in V and R bands in Table A1.
Considering that the non-thermal radiation in the optical band is dominated by synchrotron radiation, we can estimate the strength of the magnetic field as Zeng et al.(2018, 2019),Yan et al.(2018).The radiation cooling timescale (in the observer frame) of typical particles emitting synchrotron radiation can be defined as (Chiaberge & Ghisellini 1999):
where σTis the electron Thompson cross-section, and UB≡B2/8π is the magnetic energy density.The characteristic frequency can be expressed as:
In the observer frame, our observed the minimum timescale must be longer than the radiative cooling timescale.Therefore,the strength of magnetic field should be satisfied with
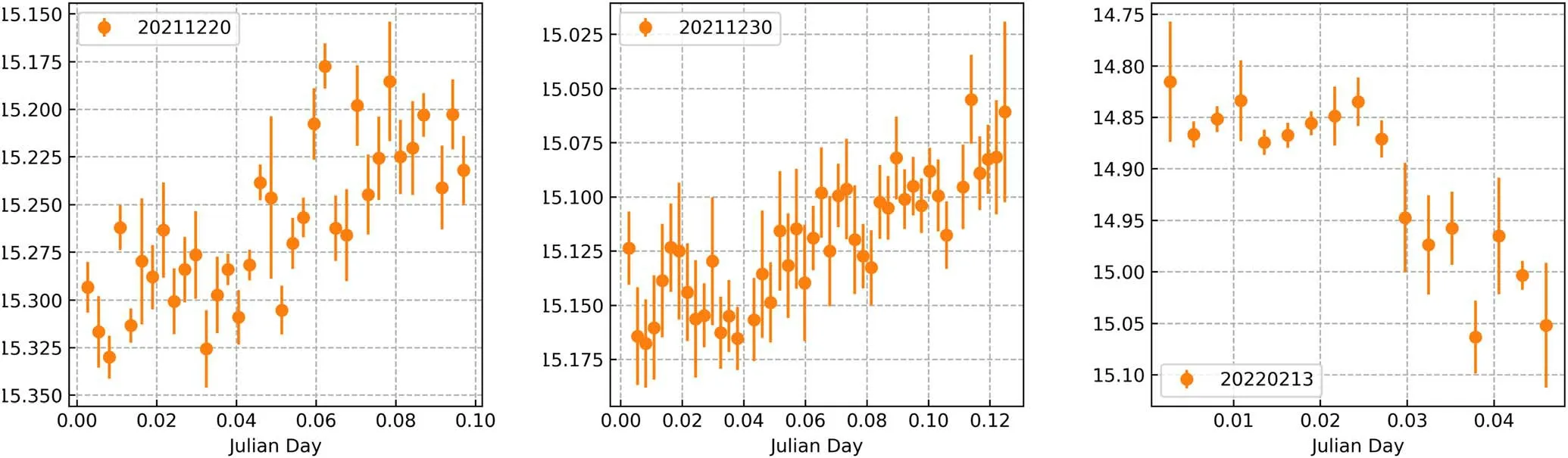
Figure 15.Intraday light curves in the R band with time in units of JD-JDstart.
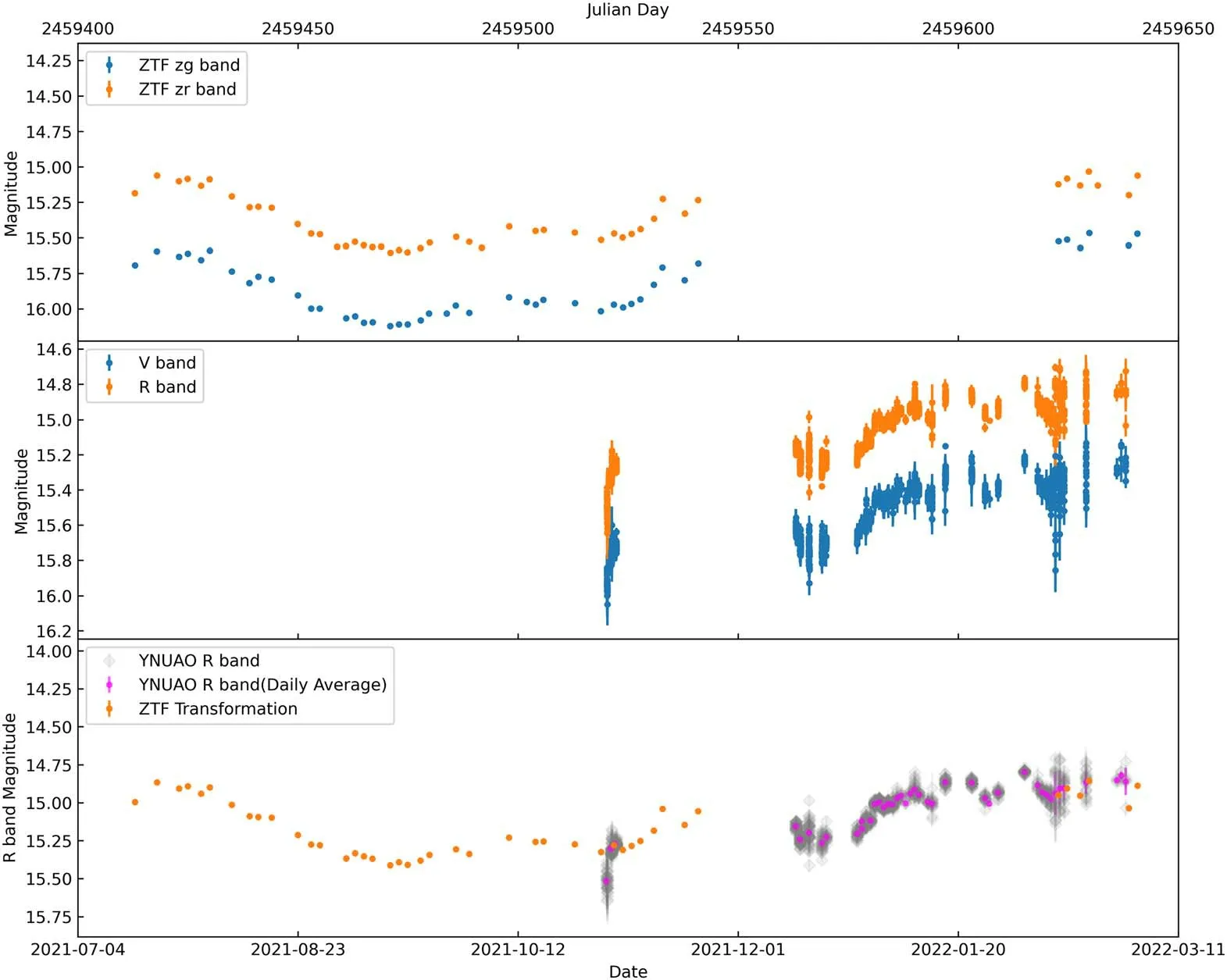
Figure 16.Light curves from 2021 July 17 to 2022 March 2.
The minimal timescales in our observation campaign were 5.82±2.74 and 6.18±2.81 minutes in the V band (as shown in Table 2),which means the magnetic field strength of the jet should be larger than 7.28 G (δD~27.09).Assuming an equipartition parameter eB≡uB/ue,which refers to the energy density of the electrons in the co-moving frame, the magnetic field can be estimated asBeB=2.9eB27G for δ=15(Böttcher et al.2005).Modeling of the overall SED with a Synchrotron Self-Compton(SSC)plus External Compton(EC)model with an external near-infrared radiation field, Abdo et al.(2011),Itoh et al.(2013) found comoving magnetic field B=0.21 ~0.35 G.Mohana et al.(2021) also determined the magnetic field as B=0.014 G(δD~27.09/21.95)through broad-band SED fitting of the two distinct states.Compared with the results by fitting the SED with the theoretical models,the magnetic field strength of the jet obtained by giving the minimum IDV timescale was much higher than expected.Therefore, the rapid variability with such a short timescale in our case may be caused by turbulence in the jet rather than by synchrotron radiation cooling.In the shock-in-jet model, a compact emission region (shock) propagates down the relativistic jet and interacts with a highly nonuniform portion in the jet flow.Any changes in the physical mechanisms of blazars, such as the accelerating particles or compressing magnetic fields, can trigger a shock that leads to optical photometric variabilities.Turbulence behind the shock-in-jet can be an excellent way to explain such minutes’timescale rapid variability of blazars (Wagner & Witzel 1995; Böttcher& Dermer 2010; Wu et al.2012; Böttcher 2021).
In our observation campaign, most of the IDVs occurred in 2021 December and 2022 February.The correlation analysis with DCF between V and R bands revealed time lags of τcent=7.70±1.47 minutes in 2021 December, and τcent=-5.18±0.16 minutes in 2022 February.These inconsistent inter-band time lags were exactly as expected by the internal-shock model for blazars (Böttcher & Dermer 2010).This semi-analytical model described the time-dependent radiative output from internal shocks arising from colliding relativistic shells in a blazar jet.Variations of specific parameters (such as the external radiation energy density, the electron equipartition fraction, the magnetic-field equipartition fraction, the electron acceleration efficiency parameter, the electron injection spectral index,and the relative Lorentz factor between the shells) may lead to changing signs of inter-band time lags,potentially explaining the lack of persistent trends of time lags in most blazars.
The relationship between the color index and magnitude is used to ascertain whether variabilities are associated with spectral changes.We investigated the color–magnitude correlation for individual nights (shown in Figures 11, 12, and 13).The individual night results showed that, in most cases, there was a negative correlation between the color index and the magnitude.Irregular variations superimposed on long-term trends led to a weak negative correlation between the color index and magnitude.As shown in Figure 10, the analysis of two time periods with obvious IDVs showed a weak negative color–magnitude correlation (with a slope of -0.40±0.05,r = -0.40 for 2021 December, and a slope of -0.16±0.05,r = -0.19 for 2022 February), which suggested redder when brighter (RWB) or bluer when fainter (BWF) behavior.Gaur et al.(2019)found a weak positive correlation, with a slope of-0.021±0.019, r = 0.13 between B and R versus R magnitude.Such a weak correlation coefficient tended to consider that the spectrums do not change with variabilities.This conclusion was also consistent with the results of Böttcher et al.(2005, 2009), no matter whether in a high optical state with R ~13.4 or a low brightness state with R ≥14.0,3C 66A did not display spectral variability.Such achromatic variation may be produced by geometric effects (lighthouse effect or microlensing effect) in the shock-in-jet model.When shocks moved toward an observer on helical trajectories in the jet, the flux variations could be produced by the sweeping beam,which usually produced achromatic variation (Camenzind & Krockenberger 1992;Wu et al.2007;Man et al.2016).Gravitational microlensing effects were from the external origin, which usually generated the light curves achromatically and symmetrically (Sun et al.2021).
3C 66A, as a TeV blazar with optical quasi-periodic variation, was also the target of multiwavelength WEBT monitoring projects and Steward Observatory AGNs Optical Observational Program.Katzman Automatic Imaging Telescope(KAIT,Li et al.2003),the LX-200 0.4 m telescope from the St.Petersburg University, and the AZT-8 0.7 m telescope from the Crimean Astrophysical Observatory(SPB and CrAO)provided long-term optical monitoring data(Otero-Santos et al.2020).Now, as one of our first batches of photometric monitoring objects with YNUAO-1 m, it can well complement the vacant observation time of the ZTF monitoring project.Figure 16 shows the light curve from 2021 July 17 to 2022 March 2, transformations between ZTF magnitudes to Johnson–Morgan system R band following Lupton et al.(2005).5https://www.sdss.org/dr16/algorithms/sdssUBVRITransform/Our data filled in gaps in ZTF observations, and continuous observational data are critical for the accuracy of the quasi-periodic analysis and multiband correlation analysis.YUNAO-1 m will also conduct long-term monitoring with VHE sources, and provide high-quality optical photometric data in conjunction with various sky survey monitoring projects.
Acknowledgments
We acknowledge the support of the staff of the Lijiang 2.4 m telescope.This work is supported by the fund for the Youth Project of Basic Research Program of Yunnan Province(202001BB050012) and the Joint Foundation of Department of Science and Technology of Yunnan Province and Yunnan University (202201BF070001-020).This research uses data obtained through the one-meter optical telescopes at Yunnan University Astronomical Observatory (YNUAO-1m) which is funded by the “Yunnan University Development Plan for World-Class Astronomy Discipline.”
Appendix
Results of the IDV Observations of 3C 66A
ORCID iDs
Wei Zeng https://orcid.org/0000-0002-4144-5378
Ben-Zhong Dai https://orcid.org/0000-0001-7908-4996
 Research in Astronomy and Astrophysics2023年4期
Research in Astronomy and Astrophysics2023年4期
- Research in Astronomy and Astrophysics的其它文章
- Period Investigation on Two W UMa Binaries HH UMa and V1175 Her
- Influence of Solar Activity on Precise Orbit Prediction of LEO Satellites
- Constraining the Temperature-density Relation of the Inter-galactic Medium from Analytically Modeling Lyα Forest Absorbers
- 3D Kinematics of Classical Cepheids According to GaiaEDR3 Catalog
- Collaborative Simulation of Mechanical Structure and Control Systems of Leighton Chajnantor Telescope
- The Variability and Radial Velocity of Planetary Nebula Central Stars
