Constraining the Temperature-density Relation of the Inter-galactic Medium from Analytically Modeling Lyα Forest Absorbers
Li Yang , Zheng Zheng, and T.-S.Kim
1 Shanghai Astronomical Observatory, Chinese Academy of Sciences, Shanghai 200030, China; liyang@shao.ac.cn
2 School of Astronomy and Space Sciences, University of Chinese Academy of Sciences, Beijing 100049, China
3 Department of Physics and Astronomy, University of Utah, 115 S 1400 E, Salt Lake City, UT 84112, USA; zhengzheng@astro.utah.edu
4 Department of Astronomy, University of Wisconsin, 475 North Charter Street, Madison, WI 53706, USA
Abstract The absorption by neutral hydrogen in the intergalactic medium (IGM) produces the Lyα forest in the spectra of quasars.The Lyα forest absorbers have a broad distribution of neutral hydrogen column density NH I and Doppler b parameter.The narrowest Lyα absorption lines (of lowest b) with neutral hydrogen column density above~1013cm-2 are dominated by thermal broadening, which can be used to constrain the thermal state of the IGM.Here we constrain the temperature-density relation T = T0 (ρ ρ¯)γ -1of the IGM at 1.6 <z <3.6 by using NH I and b parameters measured from 24 high-resolution and high-signal-to-noise quasar spectra and by employing an analytic model to model the NH I-dependent low-b cutoff in the b distribution.In each NH I bin, the b cutoff is estimated using two methods, one non-parametric method from computing the cumulative b distribution and a parametric method from fitting the full b distribution.We find that the IGM temperature T0 at the mean gas density ρ¯ shows a peak of ~1.5×104 K at z ~2.7–2.9.At redshift higher than this, the index γ approximately remains constant, and it starts to increase toward lower redshifts.The evolution in both parameters is in good agreement with constraints from completely different approaches, which signals that He II reionization completes around z ~3.
Key words: (galaxies:) intergalactic medium – (galaxies:) quasars: absorption lines – radiation mechanisms:thermal
1.Introduction
The Lyman-α (Lyα) forest, namely the ensemble of absorption lines blueward of the Lyα emission in the spectra of the quasar,is caused by the absorption of intervening neutral hydrogen in the intergalactic medium (IGM) (e.g., Cen et al.1994; Bi & Davidsen 1997; Rauch 1998).As the largest reservoir of baryons, the evolution of the IGM is affected by several processes, such as adiabatic cooling caused by cosmic expansion, heating by ionizing photons from galaxies and quasars, and heating from gravitational collapse.The Lyα forest encodes the thermal state of the IGM (Gunn &Peterson 1965; Lynds 1971; Hui & Gnedin 1997; Schaye et al.1999, 2000) and therefore it has become the premier probe of the thermal and ionization history of the IGM.
The thermal state of the IGM is usually characterized by the temperature-density relation, parameterized as T=T0Δγ-1(Hui & Gnedin 1997).Here,ρ ρΔ ≡ ¯ is the ratio of the gas density to its cosmic mean,the normalization T0corresponds to the temperature of the gas at the mean density, and γ denotes the slope of the relation.Measuring T0and γ as a function of redshift would allow the reconstruction of the thermal and ionization history of the IGM.In particular,the H I reionization and He II reionization leave distinct features in the evolution of T0and γ, and the properties of the Lyα forest contain their imprint(e.g.,Miralda-Escudé&Rees 1994;Theuns et al.2002;Hui & Haiman 2003; Worseck et al.2011; Puchwein et al.2015; Upton Sanderbeck et al.2016; Worseck et al.2016;Gaikwad et al.2019;Worseck et al.2019;Upton Sanderbeck&Bird 2020).Various statistical properties of the Lyα forest have been applied to measure T0and γ, such as the Lyα forest flux power spectrum and the probability distribution of flux(Theuns et al.2000; McDonald et al.2001; Zaldarriaga et al.2001;Bolton et al.2008; Viel et al.2009; Calura et al.2012; Lee et al.2015; Rorai et al.2017; Walther et al.2018; Boera et al.2019; Khaire et al.2019; Walther et al.2019; see Gaikwad et al.2021 for a summary).
There is also a method of measuring the IGM thermal state based on Voigt profile decomposition of the Lyα forest (e.g.,Schaye et al.1999; Bryan & Machacek 2000; Ricotti et al.2000; Schaye et al.2000; McDonald et al.2001; Rudie et al.2012;Bolton et al.2014;Hiss et al.2018;Rorai et al.2018).In this approach, the Lyα absorption spectrum is treated as a superposition of multiple discrete Voigt profiles,with each line described by three parameters:redshift z,Doppler parameter b,and neutral hydrogen column density NHI.By studying the statistical properties of these parameters, i.e., the b–NHIdistribution at a given redshift, one can recover the thermal information encoded in the absorption profiles.The underlying principle of this approach is that the narrow absorption lines(with low b)are dominated by thermal broadening,determined by the thermal state of the IGM.
Such an approach involves the determination of the cutoff in the b distribution as a function of NHI.The commonly-used method follows an iterative procedure introduced by Schaye et al.(1999):fit the observed b–NHIdistribution with a power law; discard the data points 1σ above the fit; iterate the procedure until convergence in the fit.With the small number of H I lines around the b cutoff and contamination by noise and metals, different line lists can lead to different results on the T0and γ constraints (e.g., Rudie et al.2012; Hiss et al.2018).
In this paper, we employ the low-b cutoff profile approach to constrain the IGM thermal state at z ~3.We circumvent the above problem of determining the profile of the b cutoff by proposing two different methods.The first one is a nonparametric method,which measures the lower 10th percentile in the b distribution from the cumulative b distribution in each NHIbin.The other one is a parametric method, which infers the lower 10th percentile in the b distribution from a parametric fit to the full b distribution in each NHIbin.With the determined b cutoff profiles, to derive the constraints on T0and γ, we apply a physically motivated and reasonably calibrated analytic model describing the b cutoff, which avoids using intensive simulations.Unlike previous work(e.g., Schaye et al.1999; Rudie et al.2012; Hiss et al.2018),where the low-b cutoff profile is obtained by iteratively removing data points based on power-law fits, our methods make use of a well-defined NHI-dependent low-b cutoff threshold, i.e., the lower 10th percentile in the b distribution.Adopting such a quantitative cutoff threshold allows a direct comparison to the analytic model of Garzilli et al.(2015)with the same cutoff threshold, providing a simple and efficient way of constraining the thermal state of the IGM.In this paper, we present the methods and apply them for the first time to observed Lyα forest line measurements for T0and γ constraints.
In Section 2,we describe the data used in this work,which is a list of Lyα absorption lines with Voigt profile measurements from 24 observed high-resolution and high-signal-to-noise(high-S/N) quasar spectra by Kim et al.(2021).In Section 3,we present the overall distribution of NHIand b.Then we present the two methods of determining the b cutoff profile and obtain the constraints on T0and γ in the redshift range of 1.6 <z <3.6.Finally, we summarize our results in Section 4.In the Appendix, we list the constraints in Table A1.
In this work,we analyze the fitted line parameters of the Lyα forest by Kim et al.(2021): the absorber redshift z, the(logarithmic) neutral hydrogen column density logNHI=log [NHI(c m-2)], and the Doppler parameter
2.Data Samples and Reduction Methods
b(km s-1).This list is based on Voigt profile fitting analysis for the 24 high-resolution and high-S/N quasar spectra, taken from HIRES (HIgh-Resolution Echelle Spectrometer; Vogt et al.1994; Vogt 2002) on Keck I and UVES (UV-Visible Echelle Spectrograph; Dekker et al.2000) on the Very Large Telescope (VLT).The resolution is about 6.7 km s-1.The list of quasars and the details of the fitting analysis can be found in Kim et al.(2021).

The data set from 24 HIRES/UVES quasar spectra in Kim et al.(2021) is unique in combining three aspects of the line fitting analysis: high-S/N (>45 per pixel) to reduce the possibility of misidentifying metal lines as H I absorption lines,without Damped Lyα Absorbers(DLAs)in the spectra to avoid cutting down the available wavelength region significantly and the difficulty in spectra normalization and removal of metals blended with H I, and Voigt profile fitting both from Lyα only and from available Lyman series to more effectively deblend saturated lines.As a comparison, in studying the IGM thermal state, Hiss et al.(2018) use 75 HIRES/UVES spectra at 2.0 <z <3.4 with low S/N (>15 per pixel) containing DLAs,with parameters derived from Lyα-only fit; Gaikwad et al.(2021) use 103 HIRES spectra at 2.0 <z <4.0 with low S/N(>5 per pixel) without DLAs or sub-DLAs, also with parameters derived from Lyα-only fit; Rudie et al.(2012) use 15 HIRES spectra with high S/N (>50 per pixel) containing DLAs, with parameters from fitting both Lyα and Lyβ, but only covering 2 <z <2.8.The line measurements in Kim et al.(2021) from the self-consistent, uniform in-depth Voigt profile fitting analysis with reduced systematics are well suited to our application of testing new methods of studying the IGM around z ~3.
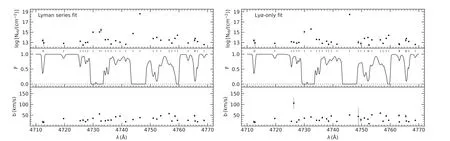
Figure 1.A portion of the reconstructed Lyα forest spectrum,using NH I and b parameters measured from QSO Q0636+6801 in Kim et al.(2021)either based on the Lyman series fit(left panels)and the Lyα-only fit(right panels).The upper and lower panels show the NH I and b measurements with their uncertainties,respectively,and the middle panels show the normalized flux with short vertical lines indicating the locations of the identified Lyα absorbers.
We refer interested readers to Kim et al.(2021)for details on the line analysis.As an illustration,Figure 1 shows a portion of the reconstructed Lyα forest spectrum from the line list of one quasar (Q0636+6801), with parameters based on the Lyman series fit (left) and the Lyα-only fit (right).For each set, the reconstructed high-resolution spectrum is shown in the middle panel.As expected, there are no noticeable differences in the reconstructed spectra from the two sets of fitting parameters,since the fitting is performed to reproduce absorption profiles.The small vertical lines in each middle panel mark the locations of individual absorbers, and the dots in the top and bottom panels are the valueslogNHIand b from Voigt fitting for these absorbers, as in the line list from Kim et al.(2021).Note that the uncertainties inlogNHIand b on the left panels are typically smaller, as not only Lyα lines but also all available Lyman series lines are used in deriving these parameters.Lyman series lines of good signal-to-noise ratios also help resolve absorption structures, especially for saturated Lyα absorptions.While this leads to small differences in the exact line lists in the left and right panels, it has little effect on the overall statistical properties of line parameters (Kim et al.2021).
We will analyze the properties of absorbers from the line list(Kim et al.2021) and use them to constrain T0and γ of the IGM thermal state.
3.Constraining the Temperature-density Relation from Lyα Absorbers


3.1.b–NH I Distribution and b Cutoff
The color-scale maps in Figure 2 show the overall distribution of NHIand b for the full absorber redshift range z ∈[1.6, 3.6] (top) and for z ~3 (z ∈[2.8, 3.2];bottom), based on the line lists from the Lyman series fit (left) and the Lyαonly fit (right), respectively.We exclude lines with b <10 km s-1as they are most likely metal line contaminants or Voigt fit artifacts5.Lines with b >100 km s-1are also excluded as they have a larger contribution from turbulent broadening than from thermal broadening.These extremely broad lines are rare and discarding them does not affect any of our results.To produce each map, we represent the likelihood of each pair of thelogNHIandlogbmeasurement as a bivariate Gaussian distribution using the measurement uncertainties and evaluate the sum of the likelihoods from all the absorbers in grid cells withΔ logNHI=0.2andΔlogb=0.01.The results are shown with a coarser grid.
The b–NHIdistributions in Figure 2 look similar to each other.The b distribution peaks around 20–30 km s-1, with a slightly higher value at the lower end of the column density.Lyα absorption lines are broadened by both thermal motion and non-thermal broadening resulting from the combination of Hubble flow, peculiar velocities, and turbulence.In many applications (e.g., Schaye et al.1999; Ricotti et al.2000;Schaye et al.2000; McDonald et al.2001; Rudie et al.2012;Boera et al.2014;Bolton et al.2014;Garzilli et al.2015;Hiss et al.2018; Rorai et al.2018; Telikova et al.2021), the narrowest Lyα absorption lines in the Lyα forests are identified and used to constrain the IGM thermal state,as the broadening of these lines is supposed to be purely thermal and the nonthermal broadening is negligible.
The narrowest Lyα absorption lines define the overall lower cutoff in the b distribution as a function of NHI.We perform such an analysis by computing the locus of the boundary of the lower 10th percentile in the b distribution in each NHIbin.The black points in each panel of Figure 2 delineate such a cutoff boundary, with error bars estimated from bootstrap resampling the data points 100 times.The black solid curve is from an analytic model developed in Garzilli et al.(2015), which describes the minimum line broadening (defined by the 10th percentile cutoff b) as the sum (in quadrature) of the thermal broadening(dotted red line)and the Hubble broadening(dotted blue line).
The analytic curve is described by Garzilli et al.(2015) as



Below logNHI~13,the data fall below the model curve.A possible cause is the incompleteness in the data—for low column density absorption systems,those with high values of b would show up as shallow absorption features in the quasar spectrum,which are hard to identify.In Garzilli et al.(2015),a 10th percentile cutoff boundary in the b–NHIdistribution for z ~3 absorbers is presented based on one OWLS simulation(Schaye et al.2010), shown as the empty triangles in each panel of Figure 2.The values of NHIand b are directly computed from the simulation data.Garzilli et al.(2020)further provide the cutoff boundary from Voigt fitting to the simulated Lyα forest spectra (see their Figure A1), which resembles the procedure in analyzing observational data.This is shown as the solid triangles in Figure 2.Compared to the case without Voigt fitting,the cutoff values of b are lowered at the low column density end.That is, at fixed, low column density, Voigt fitting tends to miss shallow absorption lines with high values of b.It is encouraging that our inferred cutoff boundary(shown with black circles)is in good agreement with their simulation-based one from Voigt fitting, including the trend at column density below logNHI~13.
We make an attempt to use the analytic model developed in Garzilli et al.(2015), i.e., Equations (1)–(4), to constrain the redshift-dependent T0and γ,the two parameters describing the temperature-density relation, T=T0Δγ-1.We first fix fN, fJ,and Γ at their fiducial values as in Equations (1)–(4) and will discuss possible systematic effects introduced by adopting these values.The cosmological parameters(Ωb,Ωm,and h)are also fixed at their fiducial values,which are consistent with the Planck constraints (Planck Collaboration et al.2020).


We use the 10th percentile cutoff in b for the parameter constraints, as the analytic model is tuned for such a cutoff threshold.Two methods are applied to estimate the 10th percentile cutoff in b in each NHIbin,a non-parametric method that directly measures the 10th percentile from the cumulative b distribution and a parametric method from fitting the full b distribution, as detailed in the following two subsections.
3.2.T0–γ Constraints from the 10th Percentile b Cutoff Estimated from a Non-parametric Method
We first present the results based on the 10th percentile cutoff profile estimated using a non-parametric method.Similar to those done in Section 3.1 and in Figure 2,at a given redshift,in eachlogNHIbin, we derive the 10th percentile cutoff boundary of b by computing the cumulative distribution function of b, where each b measurement is taken as a Gaussian distribution with the standard deviation set by the observational uncertainty.The uncertainty in the 10th percentile locus is estimated through bootstrap resampling the data points 100 times.The analytic model is then applied to constrain T0and γ.
The results are shown in the top two panels of Figure 3(labeled as “10th percentiles”), and T0and γ constraints as a function of z are found in Table A1.The red and blue points are based on b-NHIparameters measured through the Lyman series fit and the Lyα-only fit, respectively.They appear to be consistent with each other, typically within 1σ.Compared to those based on the Lyα-only fit, those based on the Lyman series fit have larger uncertainties at lower redshifts, since the number of available sightlines for the Lyman series fit is smaller.
Both the values of T0and γ show a clear trend with redshift,with a transition around z ~2.8.The temperature T0at mean density increases from ~104K at z ~1.7 to ~1.55×104K at z ~2.7, then decreases toward higher redshifts, reaching~1.15×104K at z ~3.5.The T0value at z ~3.1 for the Lyman series fit case and that at z ~3.3 for the Lyα-only fit case deviate the trend of decreasing with increasing redshifts,with T0~1.4–1.5×104K, but they are consistent with being fluctuations.For the values of γ, the broad trend appears to be decreasing from γ ~1.4–1.5 to 1.3 in the redshift range of 1.6 to 2.8–2.9 and then flattened (or maybe slightly increasing)toward higher redshifts.The transitions seen in T0and γ around z ~2.7–2.9 are signatures of He II reionization (e.g., Upton Sanderbeck et al.2016; Worseck et al.2019; Villasenor et al.2022).Photons ionizing He II heat the IGM, and the temperature T0climbs up, reaches a peak, and then drops when adiabatic expansion starts to dominate the temperature evolution.Heating the IGM makes γ decrease (e.g., γ would become unity if the IGM is heated to be isothermal)and then it increases when the effect of adiabatic expansion kicks in.
The temperature-density relation has been observationally constrained with various methods.Early constraints show large scatters and have large uncertainties.We choose to compare to a few recent constraints.As a comparison, the gray squares in the top panels of Figure 3 are from Hiss et al.(2018).They are also constrained through the low-b boundary of the b-NHIdistribution with high-resolution spectra,but by comparing to a set of hydrodynamic simulations.The overall trend is similar to ours,e.g.,a peak in T0at z ~2.8.The variation amplitude in T0from Hiss et al.(2018)appears higher than ours—while the T0values at the low- and high-redshift ends are consistent with ours, their peak T0value is much higher, ~2×104K, ~25%higher than ours(1.55×104K).Similarly,the value of γ from their constraints has a steeper drop from z ~2 to z ~2.9 (with larger uncertainties though).
Villasenor et al.(2022) constrain the temperature-density relation and the evolution of the ionization rate by fitting the Lyα forest power spectrum from high-resolution spectroscopic observations using a large set of hydrodynamic simulations.The black curves in the top panels show T0and γ constraints from their best fit model, with the shaded bands representing the 1σ uncertainty (very narrow in the γ constraints).Our results agree well with theirs in terms of the variation amplitude of T0, while the peak in our results occurs at a lower redshift(z ~2.7)than theirs(z ~3.0).The trends in γ are also similar to our results showing a slightly lower (higher) γ at low (high)redshifts.Given the uncertainties in our inferred γ values, our results are consistent with theirs.
The yellow data points are constraints from Gaikwad et al.(2021), based on four different flux distribution statistics of Lyα forests in high-resolution and high-S/N quasar spectra.Accounting for the uncertainties, our results show a good agreement with theirs.
The green curve in each panel represents the prediction from a hydrodynamic simulation in Upton Sanderbeck et al.(2016),which includes the effect of He II reionization.It almost falls on top of the constraints in Villasenor et al.(2022) for T0.It appears to be slightly lower in γ,but with a quite similar trend.The broad features predicted from this hydrodynamic simulation are similar to our results, except for the small shift in the redshift of the peak T0.
3.3.T0–γ Constraints from the 10th Percentile b Cutoff Estimated from a Parametric Fit to the b Distribution
Estimating the b cutoff directly from the cumulative b distribution, while straightforward, can have limitations.First,the IGM thermal state impacts all the lines, not just the narrowest lines.Therefore, by restricting the use of the data in the tail of the distribution near the cutoff,this approach throws away information, which can significantly reduce the sensitivity to the IGM thermal state.Second, in practice, determining the location of the cutoff is vulnerable to systematic effects,such as contamination from unidentified metal lines or misidentified metal lines as H I and noise.
To overcome these limitations, we develop an approach to infer the 10th percentile b cutoff by a parametric fit to the full b distribution in each NHIbin.To describe the b distribution,we adopt the functional form suggested by Hui&Rutledge(1999),derived based on the Gaussian random density and velocity field.It is a single-parameter distribution function,
Such a distribution function naturally explains the salient features of the observed b distribution: a sharp low-b cutoff,corresponding to narrow and high amplitude absorptions(statistically rare, related to the tail of the Gaussian distribution), and a long power-law tail toward high b, coming from broad and low-amplitude absorptions.The parameter bσmarks the transition from the exponential cutoff to the power-law part.With this distribution, the b value for the lower 10 percentile cutoff isbσ(l n 10)14.
For every redshift bin, in each NHIbin, with the observed values of b,we derive the constraints on bσusing the maximum likelihood method6We adopt the publicly available Python Package kafe2 (https://github.com/PhiLFitters/kafe2) to perform the maximum likelihood estimation..The inferred values of the 10th percentile cutoffσbln 1014( ) as a function of NHIare used to constrain T0and γ,as in Section 3.2.The results are shown in the bottom panels of Figure 3 (labeled as “b σ(l n 10)14”).The constraints on T0are similar to those inferred from using the 10th percentile b cutoff estimated from the non-parametric method.The peak is around z ~2.8 with a value of ~1.5×104K.The fluctuation in the trend with redshift is reduced, as expected,given that the 10th percentile boundary is from fitting the overall b distribution.For γ, the trend with redshift is also similar to that based on the non-parametric b cutoff estimate,but the amplitude appears to be lower.The systematic trend may reflect the fact that the analytic model is tuned for the first method, not the second one.However, for most γ values the systematic shifts are within 2σ with the data we use in our analysis.

Figure 3.Constraints on T0 and γ,the two parameters describing the temperature-density relation T=T0Δγ-1 in the IGM.Our results are shown as open circles,red(blue)circles correspond to Lyα absorber parameters NH I and b measured from the Lyman-series(Lyα-only)fit.In the top panels,our constraints are derived using the b cutoff relation estimated from the data, while those in the bottom panels are from the b cutoff relation inferred from fitting the b distribution.See the text for details.In each panel,The gray squares are constraints from Hiss et al.(2018),also from modeling the b cutoff relation,but with a set of hydrodynamic simulations.The yellow squares are from Gaikwad et al.(2021),constrained based on four different Lyα forest flux statistics.The black curve(with the 95%confidence interval shaded) corresponds to the constraints in Villasenor et al.(2022) by fitting the Lyα forest power spectrum with a large set of hydrodynamic simulations.The green curve is the prediction in Upton Sanderbeck et al.(2016) from a hydrodynamic simulation including the effect of He II reionization.The horizontal line at T0=1.5×104K or γ=1.32 is shown simply as a reference to aid the comparison.
As a whole, our derived constraints on T0and γ based on two methods of estimating the b cutoff profile broadly agree with each other.They also appear to be consistent with the results inferred by Gaikwad et al.(2021).While the main difference in our two types of constraints lies in the amplitude of γ, both of them appear to be around the Gaikwad et al.(2021) values, typically within 1σ.
We present the results here as the marginalized constraints on T0and γ,respectively.For completeness,the full constraints with both methods of deriving the b cutoff are shown in the Appendix, where we also provide Table A1 for the T0and γ constraints.
3.4.Sensitivity of the T0–γ Constraints on Parameters in the Analytic Model
In obtaining the constraints on T0and γ in Sections 3.2 and 3.3, we have fixed the model parameters fN, fJ, and Γ to their fiducial values in Equations (1)–(4).That is, we neglect their dependence on redshift.One may worry that this could introduce systematic uncertainties in the inferred T0and γ.
We can study the sensitivity of the T0and γ constraints on these model parameters by considering the low-NHIand high-NHIlimit in the model.At low NHI, where the Hubble broadening dominates, the cutoff in b is approximately

While the above tests to the sensitivity are general, they do not reflect the expected redshift dependence on the model parameters.For a more realistic assessment of the potential systematics,we turn to simple models of these parameters.The parameter fN, which is the proportionality coefficient relating NHIand the product of the number density nHIand the filtering scale λF=fJλJ, is expected to be insensitive to redshift.The filtering (smoothing) scale λFat a given epoch depends on the history of the Jeans length λJ,i.e.,on the thermal history of the IGM.Therefore, we expect fJto evolve with redshift.The photoionization rate Γ is expected to depend on redshift,as the ionizing photons come from the evolving populations of starforming galaxies and quasars.We perform further tests on the T0-γ constraints by modeling fJ(z) and Γ(z).
Gnedin &Hui(1998)derive an analytic expression of λFin linear theory,

To test the potential effect of the evolution of fJ(z)=λF(z)/λJ(z) on our constraints, we compute fJ(z) by adopting an IGM temperature evolution similar in shape to that in Villasenor et al.(2022), starting from T0~0K at z ≿7 and increasing to T0≿104K at lower redshifts with two bumps at z ~6 and z ~3 caused by H I and He II reionization,respectively.The values of fJare scaled such that fJ(z=3)=0.88 to match the fiducial value tuned in Garzilli et al.(2015).The resultant fJ(z) is ~0.9 for 2.9 <z <3.6 and ramps up toward lower redshifts to a value of ~1.27 at z ~1.6.
In the redshift range of interest here, the empirically measured hydrogen photoionization rate Γ only shows a mild evolution (e.g., Becker et al.2007, 2013;Villasenor et al.2022).We model the evolution to be Γ(z)=10-12s-1[(1+z)/2.6]-1, consistent with the model in Haardt & Madau (2012) and those empirical measurements with a steeper evolution.

Figure 4.Similar to Figure 3,but our constraints are compared to those with evolving model parameters.The red and blue open circles are the same as in Figure 3,where fJ and Γ parameters in the analytic model are fixed at their fiducial values.The pink and cyan filled circles are constraints when allowing fJ and Γ to evolve with redshift.See the text for details.For clarity,the pink and cyan points are shifted by Δz=0.05.The ratios of the latter constraints to the former ones are shown in the small panels, with the shaded regions representing the 1σ uncertainties.
The test results with the evolving fJand Γ are shown in Figure 4, in comparison with the fiducial results.For the constraints using the 10th percentile b cutoff estimated nonparametrically (top panels), T0appears to be slightly lower at lower redshifts, before reaching the peak.The value of γ is slightly higher at lower redshifts and lower at higher redshifts.Each lower small panel shows the ratio of the constraints to those from the fiducial ones, and all the changes in the constraints caused by the evolving fJand Γ are well within the 1σ uncertainty.
For the results using the b cutoff determined by a parametric fit to the b distribution(bottom panels),the trends are similar to those in the top panels, but with changes of larger amplitude.For γ, the changes are still well within the 1σ uncertainty.For T0,most of the changes are also within 1σ and others are within 1.5σ(if accounting for uncertainties in the constraints with both fixed and varying fJand Γ).For both methods, adopting the evolving fJand Γ leads to constraints more in line with those from Gaikwad et al.(2021) and Villasenor et al.(2022) at lower redshifts.
As a whole, the tests demonstrate that fixing the parameters in the analytic model to their fiducial values does not introduce significant systematic trends in the T0-γ constraints with the data we use.The amplitude and shape of the column-densitydependent b cutoff profile of Lyα absorbers atlogNHI∈ [13,15] enable robust constraints on the temperature-density relation of the IGM around z ~3 within the framework of the analytic model.
4.Summary and Discussion
Based on the distribution of the neutral hydrogen column density NHIand Doppler b parameter measurements of 1.6 <z <3.6 Lyα absorbers in the Lyα forest regions of high-resolution and high-S/N quasar spectra, we employ an analytic model to constrain T0and γ, the two parameters describing the temperature-density relation of the IGM,T=T0Δγ-1.The constraints come from the NHI-dependent low b cutoff, contributed by Lyα absorbers dominated by thermal broadening.The IGM temperature T0at the mean density shows a peak of ~1.5×104K at z ~2.7–2.9 and drops to ~104K at the lower and higher end of the redshift range.The index γ reaches a minimum around z ~3.The evolution in both parameters signals that He II reionization finishes around z ~3.
The low b cutoff profile as a function of NHIis obtained using two methods.The first one is a non-parametric method.With the measured values of NHIand b and their uncertainties,in each NHIbin,we compute the cumulative distribution of the measured b parameter to find the cutoff value corresponding to the lower 10th percentile and the uncertainty in the cutoff value is obtained through bootstrapping.The second method is a parametric one.In each NHIbin, we fit the b distribution with an analytic function (Hui & Rutledge 1999) using a maximum likelihood method to infer the 10th-percentile b cutoff value.The analytic model developed in Garzilli et al.(2015) is then applied to model these b cutoff profiles to obtain the T0-γ constraints.For T0, using the b cutoff profiles estimated from the two methods leads to similar constraints.For γ,using the b cutoff profile from fitting the b distribution results in lower values of γ than that using the non-parametrically inferred b cutoff.This may result from the fact that the analytic model is effectively calibrated with the first method.Nevertheless, the constraints of γ with b cutoff profiles from the two methods are consistent within 2σ in most redshift bins.In obtaining the constraints,we use NHIand b parameters measured from fitting the Lyman series lines and from only fitting the Lyα lines,respectively, and the results agree with each other.
Our results are in line with some recent T0–γ constraints from completely different approaches.Those include Gaikwad et al.(2021),who measure the IGM thermal state by using four different flux statistics in the Lyα forest regions of highresolution and high-S/N quasar spectra and by using a code developed to efficiently construct models with a wide range of IGM thermal and ionization histories without running full hydrodynamic simulations.Our results also agree with those in Villasenor et al.(2022), where the constraints on the IGM thermal and ionization history are obtained from modeling the one-dimensional Lyα forest power spectrum with a massive suite of more than 400 high-resolution cosmological hydrodynamic simulations.These nontrivial agreements with other work of different approaches suggest that the analytic model we adopt not only correctly captures the main physics in the low b cutoff but also is reasonably calibrated.
There are a few model parameters in the analytic model: fJrelates the Jeans length to the filtering (smoothing) scale, fNis the proportional coefficient in determining the neutral hydrogen column density from the neutral hydrogen number density and the filtering scale, and Γ is the hydrogen photoionization rate.At high NHIthat we mainly use for the T0–γ constraints, the b cutoff profiles and hence the constraints are insensitive to these parameters, e.g., with b2approximately depending on(fJ fNΓ)-0.25.We further test the sensitivity by adopting an evolving fJfactor from linear theory and an assumed thermal evolution of the IGM and an observationally and theoretically motivated Γ evolution, and we find no significant changes in the constraints.That is, adopting the fiducial values of the model parameters result in no significant systematic trend in the T0–γ constraints within the framework of the analytic model and with the observational data in our analysis.
The analytic model, with its current functional form, however,could still have systematic uncertainties in that it may not perfectly fit the results from the hydrodynamic simulations.Garzilli et al.(2020) have discussed the possible improvements to the model.While directly using simulations to perform parameter constraints(e.g.,Villasenor et al.2022)is a route to largely reduce systematic uncertainties,it would still be useful to calibrate an analytic model with a set of hydrodynamic simulations at different output redshifts.To be self-consistent,model parameters like fJand Γ should encode the dependence on the IGM’s thermal and ionization history.The model can also be calibrated to accommodate different ways of inferring the b cutoff profile, as well as different percentile thresholds for defining the cutoff(e.g.,Garzilli et al.2020).Such a model would have the advantage of being computationally efficient and can be easily applied to model observed Lyα absorbers to learn about the physical properties of the IGM.
At z ≿3, when He II reionization is not complete, a large number of sightlines are needed to fully probe the IGM state with patchy He II reionization.The sample of the 24 highresolution and high-S/N quasar spectra used in our analysis may still have appreciable cosmic variance (more exactly sample variance) effects, and the uncertainties in our T0and γ may have been underestimated.In fact, this is true for the constraints in most work.A large sample of Lyα forest absorbers from high-resolution and high-S/N quasar spectra is desired to probe the IGM state and He II reionization, which would help tighten the constraints on T0and γ and also make it possible to constrain quantities like fJand Γ.
Acknowledgments
This work is supported by the National Key R&D Program of China (Grant No.2018YFA0404503).L.Y.gratefully acknowledges the support of China Scholarship Council (No.201804910563)and the hospitality of the Department of Physics and Astronomy at the University of Utah during her visit.Z.Z.is supported by NSF grant AST-2007499.The support and resources from the Center for High Performance Computing at the University of Utah are gratefully acknowledged.
Appendix
In Figure A1, we show the constraints in the T0–γ plane for different redshift bins, using b cutoff profile estimated non-parametrically from the data (top panels) and parametrically from fitting the b distribution,with absorber NHIand b measurements based on the Lyman series fit (left panels)and the Lyα-only fit (right panels).As discussed in Section 3.4, with the relation between the b cutoff and NHI, the constraints on T0are mainly from the relation’s amplitude, while those on γ come from its shape.At each redshift, the constraints in the T0–γ show a degeneracy direction: a higher T0is compensated by a lower γ.This is easy to understand—with a higher T0(hence higher amplitude from the model), a lower γ value can tilt the model so that the amplitude of the b cutoff profile toward high NHIcan be lowered.

Figure A1.Joint constraints on the IGM temperature-density relation parameters,T0 and γ,from NH I and b values measured based on the Lyman series fit(left panels)and Lyα-only fit(right panels).The constraints in the top panels are derived using the b cutoff relation estimated from the data,while those in the bottom panels are from the b cutoff relation inferred from fitting the b distribution.The contours show the central 39% of the distribution for the two parameters.
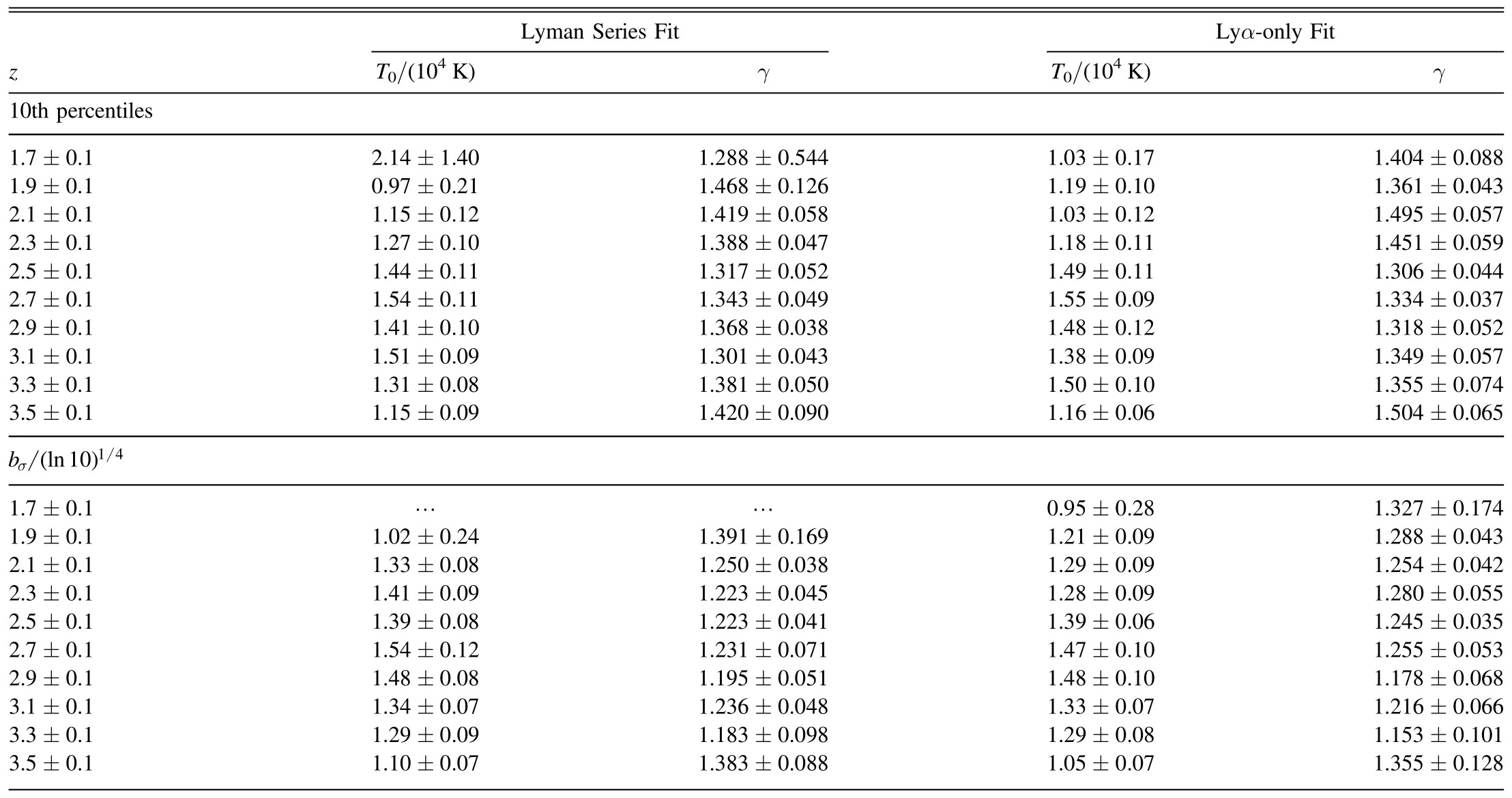
Table A1 Constraints on T0 and γ at Different Redshifts, Using NH I-dependent b Cutoff Profile Estimated Non-parametrically from the Cumulative b Distribution (“10th Percentiles”)and Parametrically from Fitting the Full b Distribution(“ σb ln 10 14( ) ”),with Absorber NH I and b Measurements Based on the Lyman Series Fit and the Lyα-only Fit
ORCID iDs
Li Yang https://orcid.org/0000-0001-5353-2957
 Research in Astronomy and Astrophysics2023年4期
Research in Astronomy and Astrophysics2023年4期
- Research in Astronomy and Astrophysics的其它文章
- Study of Central Intensity Ratio of Seyfert Galaxies in Nearby Universe
- The Variability and Radial Velocity of Planetary Nebula Central Stars
- Period Investigation on Two W UMa Binaries HH UMa and V1175 Her
- 3D Kinematics of Classical Cepheids According to GaiaEDR3 Catalog
- Influence of Solar Activity on Precise Orbit Prediction of LEO Satellites
- Photometric Monitoring of Blazar 3C 66A with the Yunnan University Astronomical Observatory 1m Telescope
