Period Investigation on Two W UMa Binaries HH UMa and V1175 Her
Linfeng Chang, Liying Zhu, and Fangbin Meng
1 Yunnan Observatories, Chinese Academy of Sciences (CAS), Kunming 650216, China; changlinfeng@ynao.ac.cn
2 University of Chinese Academy of Sciences, Beijing 101408, China
3 Key Laboratory of the Structure and Evolution of Celestial Objects, Chinese Academy of Sciences, Kunming 650216, China
Received 2023 January 18; revised 2023 February 25; accepted 2023 March 6; published 2023 April 5
Abstract HH UMa and V1175 Her are two W UMa contact binary systems whose periods were reported as undergoing secular increase.In this paper, we improved their period analyses with a more extensive database of eclipse timings,finding that both periods show cyclic variation.The cyclic variation could be attributed to a Light Travel Time Effect induced by a third body.Both circular orbit and eccentric orbit cases were considered.For HH UMa,the cyclic variation with a period of around 20 yr has been detected, which may be caused by a third body with the mass larger than 0.23 M⊙.However, no parabolic variation was detected in its O-C curve, implying the balance of the mass transfer between the two components and the angular momentum loss from the binary system.As to V1175 Her, a long-term period increase superposed on a periodic oscillation was detected.The period increase with a rate of about dP/dt=2×10-7day yr-1 indicates the mass transfer from the less massive component to its companion.The cyclic variation of about 7.5 yr could be caused by a hierarchical third body with a minimal mass exceeding 0.46M⊙orbiting around the central binary.This mass is larger than that of the less massive component of the binary,which means that the secondary component was not replaced by the third body during early stellar interactions, implying that it keeps original dynamical information.By removing angular momentum from the central binary system, the tertiary component has played a significant role in the formation of contact binaries.
Key words: (stars:) binaries: eclipsing – (stars:) binaries (including multiple): close – stars: late-type
1.Introduction
The contact binaries are these systems whose two components have filled their Roche Lobes (RLs, Kopal 1959), and share a common convective envelope (CCE, Lucy 1968b).Frequent mass and energy transfers in the CCE, result in the two components owning very similar surface temperatures,even though they may have various mass ratios (Lucy 1968a).Consequently, contact binaries usually display EW-type light curves, where the light curve changes continuously with the depths of the primary and secondary minima being nearly equal(Qian et al.2020).W UMa type contact binaries are a subtype of contact binaries comprising F, G and K type spectra(Rucinski 1993) and with short periods.Contact binaries are thought to be formed from detached binaries via angular momentum loss (AML; Qian et al.2017), and finally merged into a single star like V1309 Sco (Yakut & Eggleton 2005;Tylenda&Kamiński 2016;Zhu et al.2016;Pietrukowicz et al.2017;Liu et al.2018).In addition,the existence of extra distant companions, which could have absorbed angular momentum during the evolution of multiple systems, also results in the formation of contact binaries (Pribulla & Rucinski 2006; Qian et al.2015),thus,the third body has played a critical role for a close binary to evolve into a contact binary.
The O-C method is a common way to explore the orbital period changes of contact binaries.Secular period variations of eclipsing binaries can be investigated by analyzing the O-C diagram, which exhibits the difference between the observed eclipse timings and those computed with a given ephemeris(Liao & Qian 2010a).Many physical mechanisms of contact binaries can be revealed by studying their O-C data, such as the mass transfer in the two components, Applegate effect(Applegate 1992), Shklovskii effect (Shklovskii 1970), and light travel time effect (LTTE, Borkovits & Hegedues 1996)via dynamical effects of a tertiary component.
HH UMa (α2000=11:04:48.15, δ2000=+35:36:26.6) is a W UMa eclipsing binary indicated by Pribulla et al.(2003)with a mass ratio between 0.35 and 0.45.They noted the marked asymmetry in the light curves of HH UMa and nightto-night changes outside the eclipse.The radial velocity study of Rucinski et al.(2008)confirmed the results of Pribulla et al.(2003).Han et al.(2014) applied the W-D program to model the asymmetry light curves of HH UMa in the BV bands,indicating it is a W-type W UMa binary, and the asymmetry light curves were explained by adding a hot spot on the more massive component.Their period investigation manifested that the period of HH UMa underwent secular increase.Yılmaz et al.(2015) conducted simultaneous W-D investigation of Min =HJD2453900.5264 +0d.321156×E.Lu et al.light and radial velocity curves of HH UMa, deriving that HH UMa was an A-subtype W UMa binary, which disagreed with the result of a W-subtype from Han et al.(2014).The seasonal variations in the light curves of HH UMa were interpreted with two cool spots on the less massive component.Next, Wang et al.(2015) conducted secular photometric monitoring of HH UMa and obtained three sets of light curves spanned over six weeks.The light curves displayed obvious asymmetry and rapid interchange between the two maxima.These three asymmetry sets of light curves were modeled by assuming two cool spots on the more massive component.In addition,Wang et al.(2015) analyzed the period of HH UMa with all available minima, including their new timings, and the result showed that the period was increasing, which was in accordance with the result of Han et al.(2014).
V1175 Her (α2000=16:24:46.22, δ2000=+21:39:03.3) is another W UMa system.It was reported by Akerlof et al.(2000) as an EW-type eclipsing binary based on the data from ROTSE-I.Blattler&Diethelm(2007)confirmed it belonged to EW type binaries and gave a linear epoch as(2018) conducted the first photometric study of it in BVRI bands.Besides, their period analysis showed that the period of V1175 Her was increasing at 3.1×10-7day yr-1.
In this paper, we improved the period analyses of HH UMa and V1175 Her with the new eclipse timings derived by us.Then we discussed the possible reasons that caused the period variations of HH UMa and V1175 Her.
2.Data Acquisition
HH UMa and V1175 Her have been monitored by many telescopes.For HH UMa, photometric data can be obtained from the Transiting Exoplanet Survey Satellite (TESS) space mission (Ricker et al.2015), Wide Angle Search for Planets(SuperWASP; Butters et al.2010), All-Sky Automated Survey for SuperNovae (ASAS-SN; Kochanek et al.2017; Jayasinghe et al.2018), Hipparcos (Hip; Perryman 2009), the Kamogata Wide-field Survey (KWS4http://kws.cetus-net.org/maehara/VSdata.py) and American Association of Variable Star Observers (AAVSO5https://www.aavso.org/LCGv2/) database.In order to calculate the eclipse timings from these sky-survey data, two methods were applied.First,the Gaussian function was directly used to derive the timings for continuous observation data,such as TESS, SuperWASP and AAVSO.While for the dispersed data from ASAS-SN, KWS and Hip, splicing phase and Gaussian fit were applied.The method of reconstructing a phase with dispersed data of more than one cycle was also used in the works of Liu et al.(2015)and Li et al.(2022a,2022b).In addition, HH UMa was observed in 2007, 2008 and 2011 by the 1.0 m reflecting telescopes at Yunnan Observatories(YNOs).The observed CCD images were reduced with applying the IRAF software and differential photometry, then 5 times of light minimum were determined.In this work, we derived 217 new times of minimum of HH UMa.The 217 eclipse timings were listed in Table 1.As to V1175 Her, we downloaded its photometric data from the All Sky Automatic Survey (ASAS; Pojmanski 2002), TESS, KWS and Super-WASP.The Gaussian function was directly utilized for the continuous data from TESS and SuperWASP.The methods of splicing phase and Gaussian fit were for the data from ASAS and KWS.Then we derived 165 new eclipse timings of V1175 Her with applying these photometric data.All eclipse timings derived from these sky-survey data were tabulated in Table 2.
3.Orbital Period Analysis of HH UMa and V1175 Her
3.1.Orbital Period Analysis of HH UMa
The first period change of HH UMa was detected by Han et al.(2014), whose results meant that the period of HH UMa was increasing.In order to check the period variation of HH UMa in detail, we have collected more eclipse timings of HH UMa.
Apart from 77 minima of HH UMa from the literature (e.g.,Pribulla et al.2003, 2005; Nelson 2006; Hubscher et al.2006;Nelson 2007,2008;Yilmaz et al.2009;Parimucha et al.2009;Nelson 2010; Parimucha et al.2011; Nelson 2012; Parimucha et al.2013;Nelson 2014;Basturk et al.2014;Wang et al.2015;Nelson 2015, 2016; Tzouganatos et al.2016; Parimucha et al.2016; Nelson 2017; Bahar et al.2017; Soydugan et al.2017;Ozavci et al.2019), we derived a total of 217 new times of minimum in this work.All minima used in this paper were observed with CCD detectors, hence, the weight 1 for all eclipse timings was adopted.By applying the period from the O-C gateway, a linear ephemeris is obtained as follows:
the corresponding O-C values were displayed in the upper panel of Figure 1,which shows a marked cyclic oscillation.The oscillation probably arises from the LTTE due to a third body.Both circular orbit and eccentric orbit cases were considered.First, the circular orbit with the eccentric e=0 was considered.To begin with, the O-C trend was explained with a parabolic curve plus a cyclic variation.It is found that this combination cannot fit the values satisfactorily.Thus the O-C data were described by a linear term with a periodic oscillation.Then,based on the least-squares method,the following equation was derived:
Equation (2) means that the period of HH UMa needs to be little corrected from P=0.375493 days to P=0.37549288(5)days.In addition,the sinusoidal term shows a cyclical variation with a period of 19.25(52)yr and a projected semimajor axis of A=0.00726(39)days.All fit lines were plotted in the left hand of Figure 1.The O-C values of HH UMa computed with Equation(1)were shown in the top panel,where the solid line represents a linear fit plus a cyclic oscillation, and the dashed line means the linear correction.The (O-C)1diagram with respect to the revised linear ephemeris was exhibited in the middle panel,and the periodic variation was fitted with another solid line.After both changes were removed,the residuals were plotted in the lowest panel.All symbols showing where the eclipsing timings come from are given in this figure, where RHN-2015 (HJD2457344.99589) was from Bob Nelson’s O-C files, 〈2016〉.
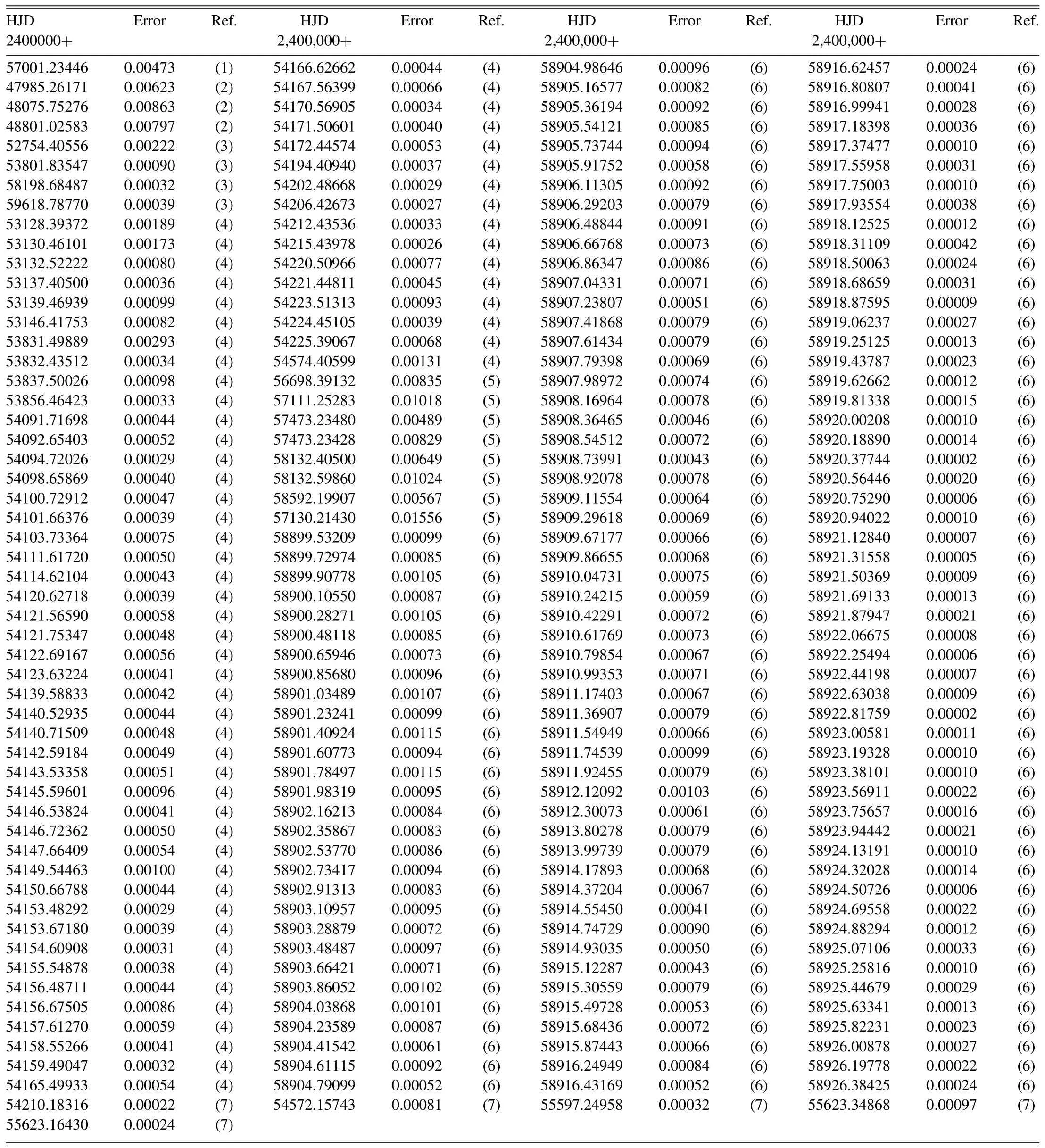
Table 1 Times of Light Minimum of HH UMa Derived in this Work
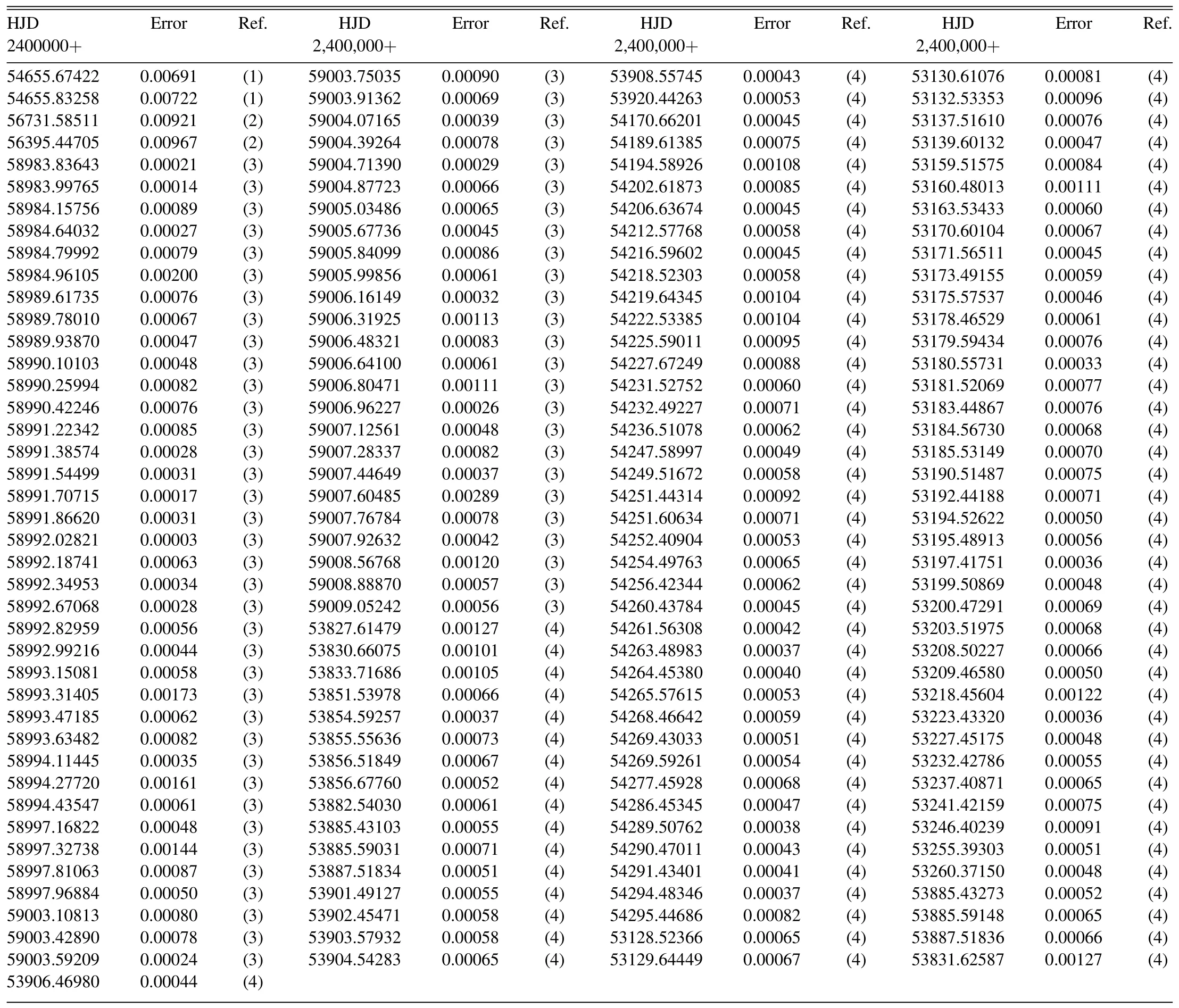
Table 2 Eclipse Timings of V1175 Her Derived from ASAS, KWS, TESS, and SuperWASP Data
Then, the periodic variation induced by the LTTE with an eccentric orbit (e ≠0) was considered.According to Irwin(1952) and Liao & Qian (2010b), the eccentric fitting of HH UMa was derived as:
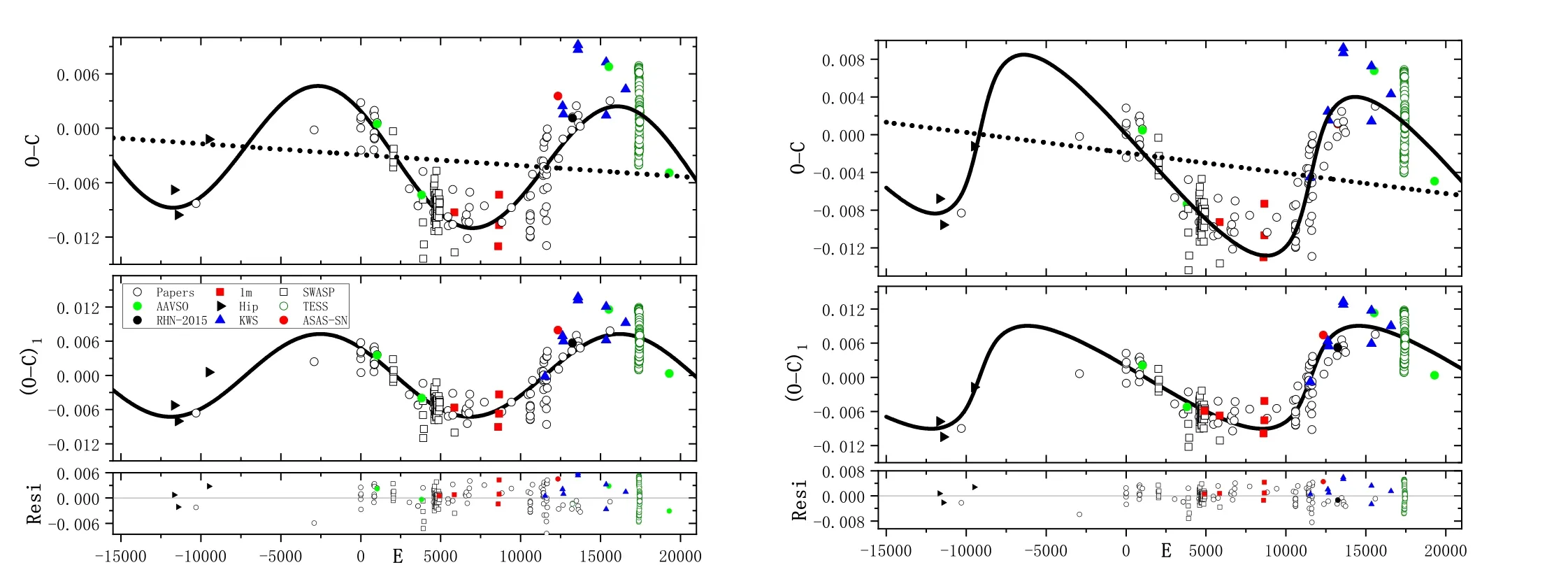
Figure 1.The O-C diagram of HH UMa.(Left)The O-C values in the top panel were computed with Equation(1).The solid line refers to a linear fit plus a cyclic oscillation(circular orbit),and the dashed line represents the linear correction.The(O-C)1 values in the middle panel are those that removed the linear fit,where the solid line presents the fit of a cyclical change.After removing the two variations, the residuals were shown in the lowest panel.The symbols which show where the minima come from are listed.The original publication of the black-filled circle RHN-2015 is unavailable online.(Right)The same as the left panels,but for the case of an eccentric orbit of the third body with e ~0.5.
with
where E is the epoch number,A=a12sini3cis the projected semimajor axis, and c is the speed of light.The rest of parameters i3, e, ν and ω are separately the inclination,eccentricity, true anomaly and longitude of periastron.The fit lines were plotted in the right panel of Figure 1, and the description is the same as that of the circular orbit.The corresponding results are summarized in Table 3.It also shows that the period of HH UMa needs to be little corrected.Here the cases of a circular orbit (i.e., e=0) of the third body, along with the eccentric orbit (i.e., e=0.50(7)), were tabulated together in Table 3.Equation(8)was used to compute the mass function of the third body, which will be introduced in Section 4.2.
One thing one may note from Figure 1 is that the eclipsing times from TESS data have a large dispersion, which arises from the rapid variations of light curves of HH UMa.The rapid variations of light curves can be explained with the presence of a starspot that changes its location over time.The light curves with strong distortion make the eclipse times deviate from the theoretical phase, resulting in different trends of the O-C values of the primary and secondary minima in the short timescale, as is seen in Figure 2, where both the O-C values from TESS data of HH UMa and V1175 Her show different trends of the primary and secondary minima.This phenomenon also occurs in binaries with variable light curves and is interpreted as spot migration, such as 32 samples from Tranet al.(2013), KIC 06,852,488 (Shi et al.2021) and NY Boo.In addition, the amplitude variation of the primary and secondary minima of HH UMa is higher than that of V1175 Her.Such a large amplitude variation also occurs in KIC 5,022,573 (Tran et al.2013).It is probable that the starspot,which changes its location over time,can always be visible in the eclipse phase, which causes such a large amplitude variation of primary and secondary minima of HH UMa.Besides, the low time resolution of 1800 s of TESS data may also bring some errors of the eclipse timings we derived.However, the dispersion of eclipsing times from TESS data has little effect on our results.
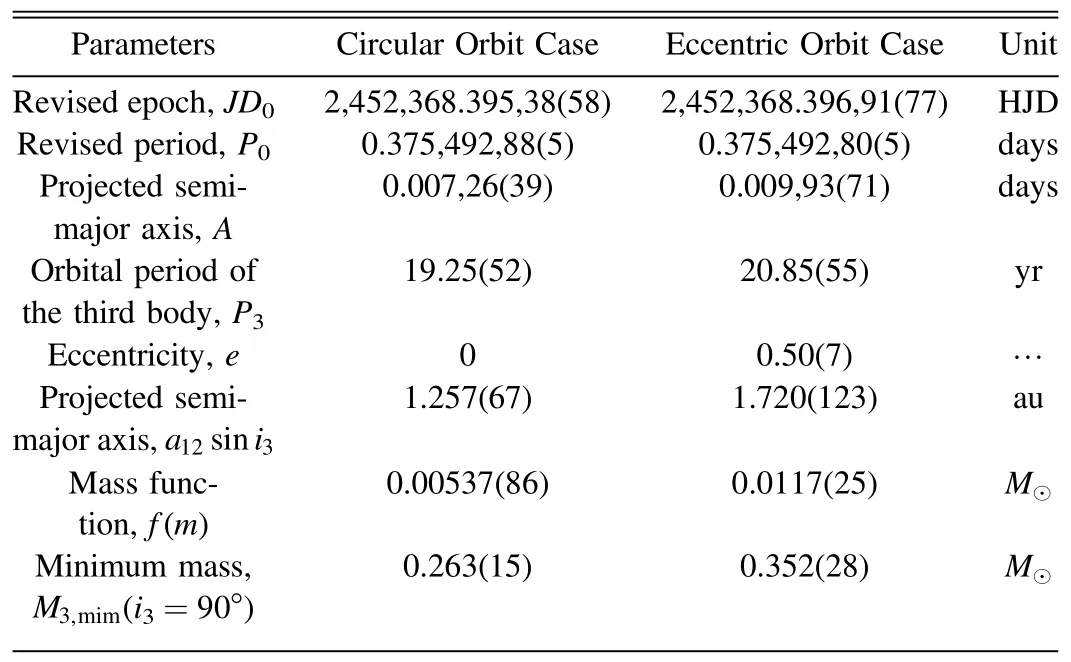
Table 3 Orbital Parameters of the Third Body in HH UMa

Figure 2.The O-C values from TESS data of HH UMa and V1175 Her.(Left)The O-C values of the primary and secondary minima of HH UMa.(Right)The same as the left panel, but for V1175 Her.
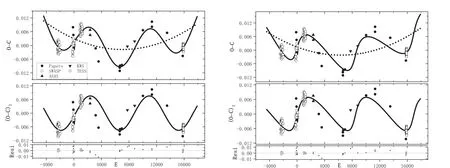
Figure 3.The O-C diagram of V1175 Her.(Left)The O-C values computed with Equation(5)are in the upper panel.The solid line represents a parabolic curve plus a cyclic oscillation for a circular orbit, and the dash line denotes the upward variation.The (O-C)1 values in the middle panel are those that removed the parabolic variation,where the solid line presents the fit of a cyclical change.After the two variations were removed,the residuals were shown in the lowest panel.The symbols which show where the minima come from are listed.(Right)The same as the left panels,but for the case of an eccentric orbit of the tertiary component with e ~0.58.
3.2.Orbital Period Analysis of V1175 Her
The first detailed study on V1175 Her was conducted by Lu et al.(2018), whose period analysis showed that the period of V1175 Her was increasing.In this study,we utilized the eclipse timings that used in Lu et al.(2018),another two from Paschke(2019) and Pagel (2021), along with 165 new ones derived by us, to derive the period variation of V1175 Her.The linear ephemeris applied is:
Here both the epoch HJD=2453900.526195 and the period P=0.32120004 were from Lu et al.(2018).According to Equation (5), the O-C values of V1175 Her were computed and shown in Figure 3, where we marked the provenances of all the eclipse timings.The general trend of the O-C diagram,as plotted in the upper panel of Figure 3, shows a pronounced fluctuation.Similarly, the cyclic fluctuation of the period of V1175 Her, caused by the LTTE due to a tertiary component,was analyzed in two cases.First, the circular orbit case was considered.It was found that the O-C trend can be well explained with the combination of a parabolic curve with a cyclic variation.The corresponding equation is:The quadratic term in Equation (6) means that the period of V1175 Her is undergoing long-term increase at a rate of dP/dt=2.17(28)×10-7day yr-1.The sinusoidal term means a cyclical variation with a period of 7.50(14)yr and a projected semimajor axis of A=0.00757(47) days.The O-C values and fitting lines were plotted in the left hand of Figure 3,where the middle panel shows the (O-C)1values, which are the values that removed the parabolic variation.After both the parabolic and cyclical variations were subtracted, the residuals were plotted in the lowest panel of Figure 3.There are no variations that can be traced from the residuals.
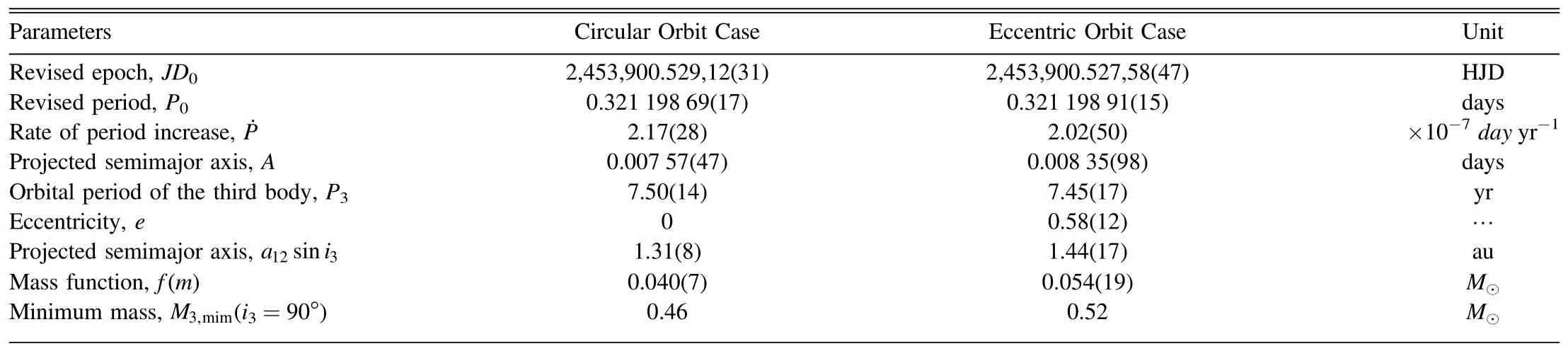
Table 4 Orbital Parameters of the Third Body in V1175 Her
Next, the eccentric orbit case (i.e., e ≠0) was considered.According to Irwin (1952) and Liao & Qian (2010b), the eccentric analysis was derived as:
where τ has been described with Equation (4).After removing the two changes, the residuals, plotted in the lowest panel,show no regularities.The parameters of the third body in V1175 Her for the circular orbit case(e=0)and eccentric case(e=0.58(12)) were listed in Table 4.The O-C data and fitting curves for both cases were plotted in Figure 3, and the interpretations are below this figure.Similar to HH UMa, the O-C values for TESS data of V1175 Her also show a small dispersion, as has been shown in Figures 3 and 2.The reason for this phenomenon is the same as that of HH UMa, because the light curves of V1175 Her also undergo variations over time.The small dispersion of TESS data also has no effect on our results.
4.Discussion and Conclusion
In this paper, we have improved the period analysis of HH UMa and V1175 Her with more extensive eclipse timings,finding the oscillations of their orbit periods that were neglected by the former researchers.
In this part, the masses of the two components of HH UMa and V1175 Her need to be applied.Thus, the masses M1=1.22(2)M⊙,M2=0.36(1)M⊙of HH UMa are taken from Wang et al.(2015).However, Lu et al.(2018) reported that M1=0.87(5)M⊙,M2=3.49(5)M⊙of V1175 Her with the G7-type spectra.The authors do not think that it is justified for a contact binary with the G7-type spectra to have a component with a mass as large as 3.49M⊙.Hence, we re-estimated the masses of V1175 Her with the mass ratio q=4 of Lu et al.(2018).The spectroscopic datum of V1175 Her was observed by the Large sky Area Multi-Object fiber Spectroscopic Telescope (LAMOST; Zhao et al.2012) on 2017 March 18,which also showed the spectral type of G7,and its atmospheric parameters (i.e.,Teff, logg, [F e H]) are very similar to those reported by the Gaia DR3(Recio-Blanco et al.2022).Thus,we downloaded the spectrum from the LAMOST,and fitted it with the University of Lyon Spectroscopic analysis Software(Ulyss;Koleva et al.2009.The stellar atmospheric parameters of the most luminous component of V1175 Her were derived as follows: Teff=5611±84 K, logg= 4.18 ±0.028cm s2,[Fe/H]=-0.25±0.05dex.
Based on the above derived stellar atmospheric parameters,the isochrone database PARSEC (the PAdova and TRieste Stellar Evolution Code, Bressan et al.2012; Tang et al.2014)was utilized to derive the mass of the component (for more detailed introduction of PARSEC, reading Zhang et al.(2019)and Zhang et al.(2020) is helpful).The mass of the more massive component of V1175 Her was obtained as M2=0.885M⊙, which is very close to the value 0.87M⊙estimated by Lu et al.(2018).Consequently, the mass of the less massive one of V1175 Her is M1=0.221M⊙with q=4.
4.1.Secular Period Changes


4.2.Cyclic Period Changes
Our above period analyses illustrate that the O-C curves of HH UMa and V1175 Her show a cyclic oscillation.Based on Kepler photometric database, Rappaport et al.(2013) estimate that at least 20%of all close binaries have tertiary components.Besides, Pribulla & Rucinski (2006), D’Angelo et al.(2006),and Rucinski et al.(2007) have carried out a statistic work on contact binaries with additional companions.Their results all showed that the presence of a third component is very common for contact binaries, manifesting “the presence of distant companions that may have acquired and/or absorbed angular momentum during the evolution of multiple systems, thus facilitating or enabling the formation of contact binaries”(Pribulla &Rucinski 2006).In addition, there are accumulated contact binaries with a third body being reported (refer to Zhang et al.(2022), Li et al.(2022a), Yıldırım (2022),Soomandar & Abedi (2021), Li et al.(2020), Bonnardeau(2020),Zhou&Soonthornthum(2019),Liu et al.(2016),Qian et al.(2014), Liao et al.(2012), Liao & Qian (2010b), etc.).Hence, it is the likeliest that the oscillations of the O-C data of HH UMa and V1175 Her are caused by the LTTE due to a tertiary component.Here,the cases of the circular orbit(e=0)and eccentric orbit (e ≠0) were considered for the LTTE.All fitting parameters, including the parameters of the third body for both cases of HH UMa and V1175 Her, were separately listed in Tables 3 and 4.According to our analyses, the period of the tertiary component in HH UMa is P3=19.25(52)yr with a projected semimajor axis of A=0.00726(39) days when e=0, and P3=20.85(55) yr with A=0.00993(71) days when e=0.50(7).As for V1175 Her, the period of the tertiary component is P3=7.50(14)yr with a projected semimajor axis of A=0.00757(47) days when e=0, and P3=7.45(17) yr with A=0.00835(98) days when e=0.58(12).The periods of the third body of HH UMa and V1175 Her, are very close in the two cases, which once again means the possibility that the cyclic oscillation caused by the LTTE is very high.
The mass of the third body can be derived with the following equation:
where f(m)is the mass function,G is the gravitational constant,m3is the mass of the tertiary component, and i3is the orbital inclination of the tertiary component.By assuming the orbital inclination of the third body is i3=90° and usinga12sini3=cA, the minimum masses of the third components in HH UMa and V1175 Her were calculated.m3,minin HH UMa and V1175 Her for both cases were listed in Tables 3 and 4.However, there was no third light being detected in Wang et al.(2015)'s and Lu et al.(2018)'s four-filter (BVRI)photometric analysis, nor did we find any stars that close to this two objects.Hence,if the cyclic oscillations caused by the third body were true, the third components in HH UMa and V1175 Her would not be luminous.In particular,m3,minof V1175 Her in both cases exceeds 0.46M⊙,which is larger than the mass of the less massive component, M1=0.22M⊙.Bate et al.(2002) pointed out that dynamical exchange interactions in a multiple system would cause the ejection of the least massive star.Hence,if a binary system encounters a body with the mass between the masses of binary’s two components, the less massive component of the binary will usually be replaced,resulting in the masses of the binary system being equalized.For V1175 Her, the mass of the tertiary component is larger than that of the less massive component of the binary,meaning that the low-mass component in V1175 Her may be the original one, and was neither kicked out during the earlier dynamical interaction nor replaced by the third body.The same case also happens to V1005 Her,which is another W UMa system (Zhu et al.2019).This information is useful to test the assumption that contact binaries were formed via dynamical interactions with other nearby stars.
In addition, the cyclic change caused by stellar magnetic activities was also considered.Then the sine functions (the circular orbit case) of HH UMa and V1175 Her were adopted.The variations of the gravitational quadruple momentum ΔQ are calculated by applying Equation (9) (Lanza &Rodonò 2002) and Equation (10) (Rovithis-Livaniou et al.2000):
Based on the known M1, M2, P and P3, ΔQ1and ΔQ2of HH UMa were computed as 5.51×1049g cm2and 1.62×1049g cm2, respectively.As to V1175 Her, ΔQ1and ΔQ2were separately determined as 1.71×1049g cm2and 6.85×1049g cm2.Lanza & Rodonò (1999) pointed out that the order of ΔQ is ~1051–1052g cm2for active binaries.The values of the ΔQ1,2of HH UMa and V1175 Her are much smaller than the typical values,which indicates that the energy produced by the magnetic activities is insufficient to induce the cyclic oscillation of the period in HH UMa and V1175 Her.Therefore, the cyclic oscillation of the period of HH UMa and V1175 Her produced by the LTTE due to a tertiary body is the most probable.However,the eclipse timings for the two targets span less than 1.5 cycles of the LTTE; thus, more high-precision minima need to be observed in the future, to determine the actual orbit parameters of the third body.
Acknowledgments
This work is supported by the National Natural Science Foundation of China (Nos.11922306 and 11933008), the International Cooperation Projects of the National Key R&D Program (No.2022YFE0127300) and the Yunnan Fundamental Research Projects (No.202201AT070180).The highprecision continuous photometric data were obtained by TESS from the Mikulski Archive for Space Telescopes (MAST), we acknowledge the team of TESS for their support in applying this enormous public open data.This work also makes use of data from LAMOST, SuperWASP, ASAS, ASAS-SN, KWS,Gaia,Hipparcos and AAVSO.We thank all the staff that work for these telescopes for providing the public data.
ORCID iDs
Fangbin Meng https://orcid.org/0000-0002-8320-8469
 Research in Astronomy and Astrophysics2023年4期
Research in Astronomy and Astrophysics2023年4期
- Research in Astronomy and Astrophysics的其它文章
- 3D Kinematics of Classical Cepheids According to GaiaEDR3 Catalog
- Photometric Monitoring of Blazar 3C 66A with the Yunnan University Astronomical Observatory 1m Telescope
- Influence of Solar Activity on Precise Orbit Prediction of LEO Satellites
- Constraining the Temperature-density Relation of the Inter-galactic Medium from Analytically Modeling Lyα Forest Absorbers
- Collaborative Simulation of Mechanical Structure and Control Systems of Leighton Chajnantor Telescope
- The Variability and Radial Velocity of Planetary Nebula Central Stars
