Physical Parameters of W UMa Type Contact Binaries and Their Stability of Mass Transfer
Berikol Tekeste Gebreyesus and Seblu Humne Negu
1 Space Science and Geospatial Institute(SSGI),Entoto Observatory and Research Center(EORC)Astronomy and Astrophysics Department,P.O.Box 33679,Addis Ababa, Ethiopia; berikoltekeste@gmail.com
2 Addis Ababa University, P.O.Box 1176, Addis Ababa Ethiopia; seblu1557@gmail.com
Abstract In this study, we determined the physical parameters of W UMa type contact binaries and their stability of mass transfer with different stellar mass ranges over a broad space by applying the basic dynamical evolution equations of the W UMa type contact binaries using accretor and donor masses between 0.079 and 2.79 M⊙.In these systems,we have studied the three subclasses of W UMa systems of A-,B-and W-type contact binaries using the initial and final mass ranges and we investigated different stellar and orbital parameters for the subclasses of W UMa systems.We examined the stability of the W UMa type contact binaries using the orbital parameters such as critical mass ratio, Roche lobe radius of the donor star and mass ratio of these systems.Thus, we computed the observed and calculated physical parameters of A-,B-and W-type W UMa systems.Moreover,we determined the combined and color temperatures to classify the three subclasses of the systems.Also, we presented the result of the internal stellar structure and evolution of W UMa type contact binaries by using the polytropic model.
Key words: (stars:) binaries (including multiple): close – (stars:) binaries: general – stars: evolution – stars:fundamental parameters –stars: early-type –stars: late-type –stars: low-mass –stars: luminosity function – mass function – stars: mass-loss
1.Introduction
A contact binary (CB) is a binary star whose two components are so close to each other that they merge to share their gaseous envelopes and they are gravitationally bound to each other (Duerbeck 1984; Muller & Kempf 1903).There are special types of CB stars, the most ample of which are W Ursae Majoris(W UMa)type(Mochnacki 1981).The W UMa type CBs are called low mass binaries and they include two stars bound together and orbiting around their barycenter(Boyajian et al.2016).All stars in the W UMa type CBs are dependent on the mass transfer between the components of the three subclasses (A-, B-, and W-type) of W UMa system via the physical principle of Roche lobe overflow (RLOF).
In the subclass of W UMa type CBs, the components of the two stars share the same Roche lobe surface as a consequence of these systems.The stars in these systems fill their Roche lobe then gas flows from the outer layers of that star through the inner Lagrangian point that connects the two Roche lobes.The Roche lobe allows the mass transfer between components of W UMa type CBs(Eggleton 1983).The structures of stars in these systems have different properties from a single star,because of the mass transfer between the components of these systems.
The physical parameters of W UMa type CBs were studied with the evolution and stellar structure of the stars using the initial and final mass ranges of the W UMa systems.Depending on the improvements in stellar theories and observational data of W UMa type CBs,there are the mass radius relation(MRR)and mass luminosity relation (MLR) which have been studied by Demircan & Kahraman (1991), Cester et al.(1983),Gimenez & Zamorano (1985), Yildiz (2014), Sun et al.(2020).But in this study we focus on the investigation of those relations and other relations such as luminosity temperature relation (LTR), radius temperature relation (RTR) and mass temperature relation(MTR)using the theoretical zero-age main sequence (ZAMS) and terminal-age main sequence (TAMS)models with empirical relations.
Here, in this study we utilized the catalog of Yildiz (2014)and the late-type W UMa CB catalog of Sun et al.(2020).The catalog of Yildiz (2014) has different subclasses of W UMa type CBs such as A-type and W-type systems (Binnendijk 1970; Van Hamme 1982) whereas the catalog of Sun et al.(2020) has different subclasses of W UMa type CBs such as A-, B-, and W-type systems (Lucy & Wilson 1979).In these two catalogs, the primary components in the A-type are hotter than the secondaries, so an A-type binary has a hotter star and their orbital period is between 0.4 and 0.8 days (Binnendijk 1970)whereas the primary component of W-type is cooler than the secondary component and it has a shorter orbital period in between 0.22 and 0.4 days (Binnendijk 1970).The spectral types of A-and W-type W UMa type CBs are A-F and G-K (Webbink 2003; Rucinski 2004), respectively.Moreover,in the catalog of Sun et al.(2020)the B-type is in poor thermal contact, although it has different effective temperatures of the components which are significant (Lucy & Wilson 1979, Sun et al.2020).The B-type of late-type W UMa CBs comes from the similarity of their light curves (Lucy & Wilson 1979).
In this study, we computed the observed and calculated parameters of 100 and 2314 stars from the catalog of Yildiz(2014) and Sun et al.(2020), respectively.In these two catalogs, we have studied orbital and stellar parameters to examine the stability of mass transfer and the evolution of the stars.
In the present work,we have examined the orbital and stellar parameters of the three subclasses of W UMa type CBs using the initial and final mass range of these systems.Hence, we computed angular momentum loss (AML), critical mass ratio,Roche lobe radius of the donor star,mass ratio,semimajor axis for the accretor and donor stars, radius, luminosity and effective temperature, age of the stars, and combined and color temperature using the range of initial and final masses between 0.079 and 2.79 M⊙(Yildiz 2014; Sun et al.2020).Also, we investigated the internal stellar structure of W UMa type CBs using the polytropic model of the system which studies the internal part of the donor stars by introducing stellar structure models in W UMa type CBs (Chandrasekhar &Chandrasekhar 1957).
The aim of this study is to make a statistical analysis of orbital and stellar parameters of the W UMa type CBs by using the catalog of Yildiz (2014), Sun et al.(2020).Also, we examined the internal stellar structure of W UMa type CBs employing the polytropic model.In these systems, we determined the evolution and stability of mass transfer by applying the ZAMS and TAMS models.
This paper is organized as follows:In Section 2 we describe the orbital and stellar parameters of W UMa systems.In Section 3 we make a statistical analysis of W UMa type CBs’parameter distributions, construct distributions of the stellar and orbital parameters of the systems between the theoretical ZAMS and TAMS models, and compare them with the empirical relations.In Section 4, we present the results and also we parameterize the parameters of those selected systems from the catalog of W UMa type CBs, and then compare the results with the theoretical relations.The conclusions are drawn in Section 5.
2.Orbital and Stellar Parameters of W UMa Type CBs
2.1.Basic Equations of Orbital Parameters
Variation of the orbital parameters with loss of mass from stars is investigated.We consider the accretor mass (Ma) and donor mass(Md)orbiting each other under the force of gravity.The orbital angular momentum of the W UMa system is given by Soberman et al.(1997), Siess et al.(2011), Eggen (1961)

A system should satisfy Kepler’s third law to express the orbital period and semimajor axis of the W UMa type CBs.Then, the orbital period of a W UMa system is expressed as
2.1.1.Roche Lobe Model
The Roche lobe is a region where the material is bound to the star by gravity.The equivalent radius of the RLOF of W UMa type CBs is defined based on the radius of a sphere with the same volume and range of mass ratios.The radius of the Roche lobe is given by Eggleton (1983)
where RLdis the Roche lobe radius of the donor star.
It is difficult to distinguish between the two stars for the purpose of calculating the masses and radii.A simpler approximation of Roche lobe radius of the donor star in Equation (3) which works well for 0.1 <q <0.8 is stated by Paczynski (1971).
2.1.2.Age of W UMa Type CBs
The basic thing needed to derive the age of the stars is the process of mass transfer between the two components of the W UMa type CBs.In a W UMa system, the mass is being transferred from the more massive accretor star to the less massive donor star, so the age of the W UMa type CB will be changed (Bilir et al.2005).The star’s age cannot be measured,and it is only estimated based on the approximation of the main sequence(MS)relation(Soderblom 2010;Van Eylen et al.2016;Negu & Tessema 2018).
2.1.3.Critical Mass Ratio of W UMa Type CBs
In a W UMa system, the critical mass ratio mainly depends on the mass transfer,AML and stellar wind of the W UMa type CBs (Chen & Han 2008; Arbutina 2009).The critical mass ratio for W UMa type CBs is predicted as
where Mcis core mass of the CB star as noted by Chen&Han(2008),and we used the core mass Mc=0.35 M⊙for the CBs.
2.2.Stellar Parameters of the W UMa Type CBs
The value of each mass in these systems strongly depends on the evolutionary phase of the mass losing star at the beginning of the mass loss transfer and the final stage process of A-, Band W-type W UMa CBs.
Case 1: MRR and MLR- To determine the radius of the W UMa type CBs,we used the initial and final mass from the two catalogs.The radius of the star was increased or decreased based on the mass transfer between the components of these systems (Gimenez & Zamorano 1985).
Thus,we investigate the radius based on the mass of A-,Wand B-type W UMa CBs.We illustrate the result of the initial and final luminosity for A-, B- and W-type W UMa CBs(Cester et al.1983) by calculating the luminosity of the stars and we compare them with the luminosity of the Sun(L⊙=3.846×1026W) (Demircan & Kahraman 1991,Harmanec 1988).

Case 2: LTR and RTR- If the stars have low mass,the luminosity will be decreased, consequently the temperature will also be affected (Demircan & Kahraman 1991;Cester et al.1983; Gimenez & Zamorano 1985).To get the effective temperature of W UMa type CBs,we used the Stefan-Boltzmann law for the luminosity of stars.

2.3.Combined and Color Temperature
In the previous studies, Sun et al.(2020) made statements about the combined and color temperatures, but they did not calculate these parameters.Rather, they only give direction on how to calculate the two parameters.The combined and color temperatures are used to examine the subclasses of W UMa type CBs and their spectral type with the period luminosity relation.

2.4.Stability of Mass Transfer in W UMa Type CBs
The stability of the mass transfer depends on the donor mass loss and donor radius of the donor star and how the conservative process operates, and also depends on the AML process as well as Roche lobe of the donor star of W UMa type CBs.For the mass transfer to continue, the donor must remain within the Roche lobe and then the W UMa type CBs are stable(Hjellming & Webbink 1987; Webbink 1985).Two things are happening at the same time that affect the stability of mass transfer in W UMa type CBs:
1.The mass-losing star changes its radius and,
2.The AML could be transferred between the components of the subclass of W UMa type CBs via the donor response
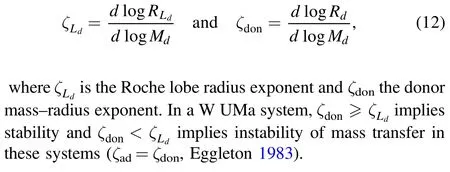
2.5.Internal Stellar Structure Equation for W UMa Type CBs
In this section,we investigate the stellar structure equation of the donor stars in W UMa type CBs which is used to study the internal part of the stars with the polytropic model.In the polytropic model, different numbers of indexes are used to explain the internal stellar structure of the donor stars and the relation between the physical parameters of W UMa type CBs with stable mass transfer(Lane 1870;Emden 1907;Sirotkin&Kim 2009).A polytropic model of W UMa type CBs is applied to investigate how the pressure of the stars changes with density inside as one moves through the W UMa system.However, we describe the polytropic model as an approximation that represents the equation of state of the gas inside stars (Chandrasekhar & Chandrasekhar 1957).The polytropic stars have a relation between the pressure and density of W UMa type CBs.Using the central density of W UMa type CBs,ρc, we have the polytropic model, which is expressed as

The appropriate boundary conditions from applying a polytropic model relation using Equation (14) are at the center of W UMa type CBs.
When pressure and density go to zero in Equation (14), the surface of the polytropic model is located at ξ=ξ1, where θ(ξ1)=0.There is an analytical solution for different polytropic indexes n=0, 1, 5.
3.Physical Parameter Distribution of W UMa Type CBs
In this section, we are applying the basic equation of the mass transfer and stellar structure models, then we design the theoretical framework for the evolutionary computations of mass transfer in W UMa type CBs.The analysis relies on our main sample of data on W UMa type CBs from the catalogs of Yildiz (2014) and Sun et al.(2020), and we summarize the details of the observations and calculated parameters in Tables 2 and 3.
3.1.Distribution of Orbital Parameters
In the evolution of W UMa systems, there are different orbital parameter distributions of W UMa type CBs.
Some orbital parameters for these systems are semimajor axis, orbital period, Roche lobe radius of the donor star and orbital angular momentum of the system.We determine the orbital parameters by using different initial and final mass ranges and comparing their results with the numerical solution of W UMa type CBs in Section 4.1.
The left side of Figure 1 shows distribution of the semimajor axis in late-type W UMa CBs with the different ranges of final donor masses.The result of this plot shows the distribution of semimajor axis with variation of color lines.The variation of colors is used to identify the subtype of late-type W UMa CBs.In this result, the semimajor axis of late-type W UMa systems shows the expansion and shrinking of A-, B- and W-type latetype W UMa type CBs.The solid black line represents W-type stars with its peak at 172.0, and the corresponding range is between 1.936 R⊙and 2.103 R⊙.
The right panel of Figure 1 shows the distribution of critical mass ratio for the final stage of donor mass of late-type W UMa CBs.Based on the mass of the stars from the catalog of Sun et al.(2020) and the core mass of CB stars, we calculated the critical mass ratio of late-type W UMa CBs utilizing Equation (6).The critical mass ratio is used to determine the stability of the mass transfer in W UMa systems.The peak point for the solid black line is 148 which indicates the number of W-type CBs that exist at that point and qcris between 0.625 and 0.6417.
3.2.Distribution of Stellar Parameters
In the evolution of W UMa systems there are different stellar parameter distributions of W UMa type CBs.Some stellar parameters of these systems are luminosity, radius, effective temperature, and combined and color temperature.

Figure 1.The distribution of calculated semimajor axis with the different ranges of donor mass by applying Equation (2).The right side shows the distribution of critical mass ratio of A-, B- and W-type late-type W UMa CBs with the donor mass Md <0.7 M⊙using the catalog of Sun et al.(2020).

Figure 2.The distribution of the accretor effective temperature with different ranges of donor masses for the left side of Figure 2 and distribution of the donor effective temperature using different ranges of initial accretor mass of W UMa systems based on the catalogs of Sun et al.(2020)and Yildiz(2014)by applying Equation(9).
The left panel of Figure 2 displays the distribution of accretor effective temperature using the donor mass range Md<0.7 M⊙.The A-, B- and W-type late-type W UMa systems have different effective temperatures in the MS regions.The result, the solid black line, features a peak point at 189.0 which is in between 3.645 K and 3.650 K for W-type systems.The solid red line corresponds to B-type systems with high effective temperature and it is a hot star compared to the other types of W UMa CBs.
The solid blue line shows the A-type star has moderate effective temperature and the solid black line of W-type of latetype W UMa CBs has cool effective temperature.The W UMa type CBs for A- and W-type have identical effective temperature, but there are slight differences between them(Yildiz 2014).The right panel of Figure 2 shows the variation of effective temperature of the donor stars for A-and W-type of W UMa CBs.The black dashed and solid black line distribution depicts the effective temperature for an A-type W UMa system and it has cool effective temperature compared to the corresponding W-type W UMa system.The W UMa type CBs,represented by the solid blue line of W-type,have a peak at 6, which is in between 3.539 K and 3.567 K.
4.Result and Discussion
4.1.Numerical Solution of W UMa Type CB Parameters
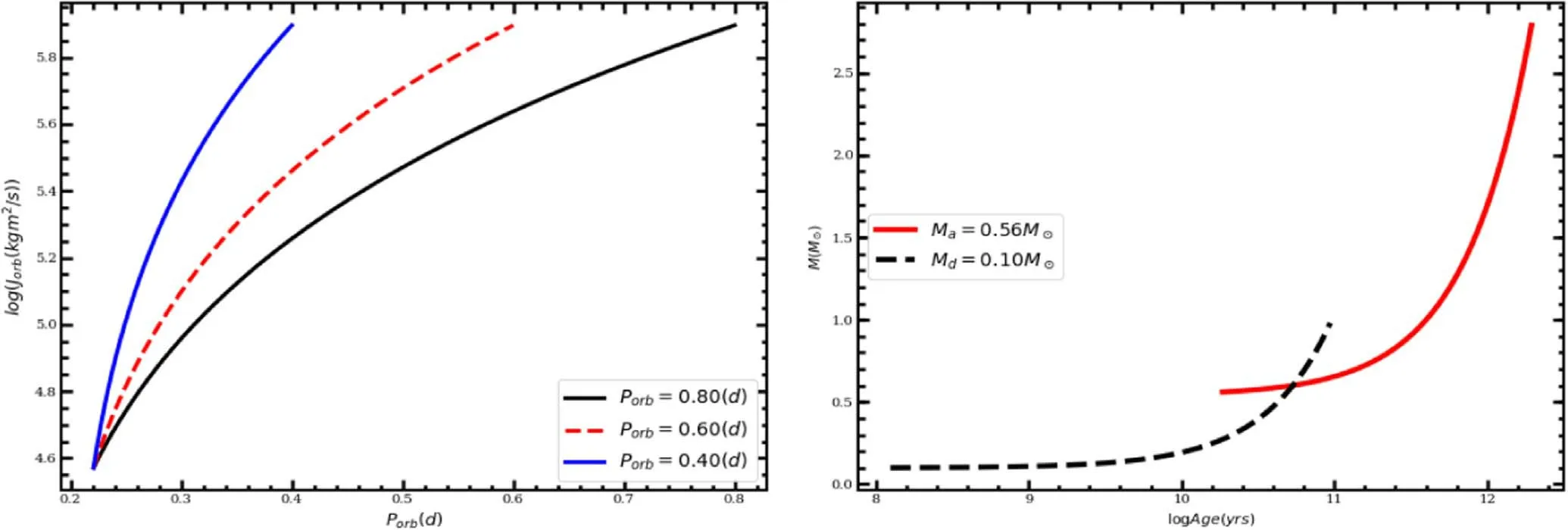
Figure 3.The numerical result of the orbital period and AML of the late-type W UMa CBs using the catalog of Sun et al.(2020)and mass age relation with different range accretor mass of W UMa type CBs using the catalog of Yildiz (2014).
The orbital angular momentum is used to determine the evolution of W UMa type CBs.The rate of change of AML increases as the orbital separation and orbital period decrease and then for AML decreases the total mass of the system also decreases (Smith 2006; Patterson 1984).The left side of Figure 3 shows the numerical solution of orbital period and orbital AML relation by applying Equations (1) and (2) using different ranges of orbital periods Porb=0.80,0.60 and 0.40 d.AML has direct or indirect relation with different orbital parameters, although for short orbital period the mass is high and the AML is also high, so orbital period and AML have an indirect relation.As we observed from the result, the short orbital period of the systems and the AML mechanism were governed by gravitational radiation (Patterson 1984; Taam &Spruit 2001).
The right panel of Figure 3 features the numerical solution of the final mass distribution and age relation of the W UMa type CBs by applying Equation (5).The dashed black line with Md=0.1 M⊙has low mass and it has slow fusion to use in the core hydrogen burning.It has less pressure, low effective temperature and also low luminosity because these stars have a long lifetime on the MS range.The solid red line represents a more massive star with Ma=0.56 M⊙, so the solid red line corresponds to a short lifetime,with higher central temperature and high pressure to support itself against gravitational collapse and also has fast fusion to use in its core for hydrogen burning.Hence,the more massive stars have a short lifetime on the MS(Soderblom 2010).The A-type shows a long lifetime and the W-type also shows a short lifetime because of the mass difference The W-type is hotter, more massive and more luminous than the A-type W UMa CBs.
4.2.The Comparison of Initial and Final Stellar Parameters
Case 1:MLR and MRR-The left side of Figure 4 depicts the distribution of initial mass–luminosity relation of W UMa type CBs depending on the theoretical model of ZAMS and TAMS with an empirical relation.In these relations we incorporated the numerical solution oflogL(a,i) andlogL(d,i) with Ma,iand Md,i, where i is for initial.In the ZAMS model we used x=3.92 for Ma,i≥0.7 M⊙, and for the TAMS model we used y=2.62 and Ma,i<0.7 M⊙.The solid black and red lines representlogL(a,i) andlogL(d,i) respectively with x=3.92,although the solid blue and black dashed line corresponds to log(La,i) andlog(Ld,i) with y=2.62 for different initial mass ranges.
The right side of Figure 4 shows the theoretical result of MRR using different initial accretor mass ranges.In W UMa systems the more massive stars have large radius and less massive stars have low radius,therefore,the radius and mass of W UMa stars have a direct relation.The radius of W UMa type CBs is utilized to examine the phase of stars in the MS region.Using Equation (9) we calculate the initial and final radius of the W UMa type CBs with the theoretical models of ZAMS and TAMS.
Case 2:LTR and RTR-The left panel of Figure 5 shows the numerical solution of distribution final donor LTR.Hence,using different donor mass of W UMa systems Md=0.58,0.78 and 0.98 M⊙, we obtained a different luminosity distribution for W UMa type CBs.The solid red line shows a more massive star with high luminosity as well as high temperature.The right panel of Figure 5 displays results of accretor radius RTR using different range accretor masses, Ma=2.79 M⊙, Ma=2.29 M⊙and Ma=2.49 M⊙.However, as we observed from this result when the mass increases, the radius also increases, but the temperature will decrease.As we observed from the result, the solid black line represents a more massive star than the other and it has lower temperature but larger radius.The solid blue line shows low radius as well as high temperature.

Figure 5.The two numerical results show the luminosity effective temperature relation, and radius effective temperature relation with different ranges by applying Equation (9) using the catalog of Yildiz (2014).
The left side of Figure 6 shows a solid black, blue and red lines and a dashed black line to represent how the radius responds to the adiabatic (ζad) calculations using theoretical ZAMS and TAMS models with empirical relations by using the donor mass.The right side of Figure 6 displays solid black,red and blue lines to represent how the donor mass responds to the adiabatic (ζad) calculations with constant mass loss rates at Md=0.98, 0.78 and 0.58 M⊙.
Comparing both plots, the star with lower mass will have a longer stability period than the star with greater mass.In a W UMa system,ζdon≥ζLd, implies stability andζdon<ζLdimplies instability of mass transfer in these systems(ζad=ζdon) (Eggleton 1983).These two plots depend on the donor mass of the star because ζaddepends on the mass loss for the donor star althoughζLdalso depends on the AML processes for W UMa type CBs.
The left side of Figure 7 shows that the solid black and red line represents the relation between the semimajor axis and orbital period of A-, W- and B-type CBs.Hence, we classified the numerical solutions of the semimajor axis and orbital period based on the donor mass Md<0.7 M⊙of the late-type W UMa systems (Sun et al.2020).In these results the stars are compacted in one region;this shows less semimajor axis and a short orbital period for the W UMa systems.Kepler’s first law states the mass-orbital period relation of the star.
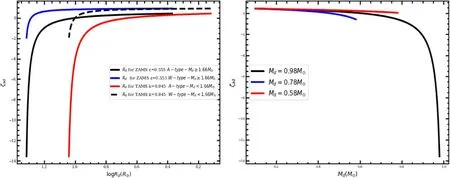
Figure 6.The two numerical result plots demonstrate radius and donor mass response to the adiabatic(ζad)calculation,with the timescale of the W UMa type CBs by applying Equation (12) using the catalog of Yildiz (2014).

Figure 7.The comparison of orbital period—semimajor axis relation and mass-orbital period relation for A-, B- and W-type of W UMa CBs with donor mass Md <0.7 M⊙by applying Equation (2) (Sun et al.2020).
As Kepler’s law states,if a star is more massive it has a short orbital period and when a star has a low mass, it has a long orbital period.Based on Kepler’s laws,the orbital period of the late-type W UMa CBs are dependent on the mass of the stars.The right side of Figure 7 shows the final phase distribution of orbital period-donor mass of the late-type W UMa CBs compared with A-, B- and W-type CBs.The A-type of latetype W UMa CBs has a long orbital period and W-type has short orbital period (Van Hamme 1982).The solid blue line shows the numerical solution of these systems.
The left side of Figure 8 shows the comparison between the distribution of the combined temperature and the calculated effective temperature of the late-type W UMa CBs that can be obtained from the catalog of Sun et al.(2020).In the result the blue-colors for B-type are dominated by the red-color of A-type, which happens because they have identical combined and effective temperature.
The right side of Figure 8 shows the comparison between the color and effective temperature relation of the late-type W UMa CBs.However, using color temperature, we have illustrated either the stars are living in the MS region or they are out of the MS region (Pecaut & Mamajek 2013).Stars with high mass will have fast hydrogen burning with short lifetime, and they will have hotter temperature as well as being bluer (Bell et al.2012; Gullbring et al.1998).Some of the stars have red color because they are the stars that decrease in temperature and also have slow hydrogen burning in the core.This aspect makes the stars have red color in the MS(Bell et al.2012;Gullbring et al.1998).

Figure 9.The result of orbital period and semimajor axis relation in the left panel and the right panel shows the mass and semimajor axis relation that can be obtained from the catalogs of Sun et al.(2020) and Yildiz (2014).In these results, the distribution shows the fitting function by applying the power-law function=a(x)b.

Table 1 The Properties of the Lane–Emden Solution Using Different Polytropic Indexes
The left side of Figure 9 shows the distribution of the orbital period and semimajor axis relation that can be obtained from the catalog of Sun et al.(2020) using different parameters of these systems.In the fitting function there are different types of relations.Some of them are linear, exponential, power-law,quadratic and others.In this thesis, we utilized a power-law fitting function.This function was used to investigate the error of the catalog of parameters from the catalog of Sun et al.(2020).
The right side of Figure 9 displays the fitting function of semimajor axis and mass of the W UMa type CBs using the catalog of Yildiz (2014).To illustrate the error of the given data, we used a power-law fitting function with different fitting parameters“a”and“b.”The solid black line shows the relation between the semimajor axis and the mass of the W UMa type CBs and the solid red line indicates the error function.

Figure 10.Numerical solution of the internal stellar structure of the W UMa type CBs for a donor star by the using Lane–Emden equation, Equation (14)with different polytropic indexes n=0, 1, 1.5, 2, 3 and 4 (Lane 1870;Emden 1907).
4.2.1.Internal Stellar Structure of W UMa Type CBs
We explain the internal stellar structure of W UMa type CBs using the polytropic model.In a polytropic model, different number of indexes are used to explain the internal stellar structure and the relation between pressure, radius, density,temperature and mass transfer in W UMa type CBs with a donor star (Lane 1870; Emden 1907; Sirotkin & Kim 2009).For n=0 the density is constant and the pressure is also constant,when n=1 the density of the star keeps the radius the same no matter what the mass is in the system and also the radius is independent of mass and the temperature is also constant;for n=5 the radius,mass,central density and central pressure are infinite, therefore, the binding energy is infinite.
Table 1 shows the result of the polytropic case using the Lane–Emden equation for each polytropic index, where
Figure 10 shows the numerical solution of the Lane–Emden equation by Lane(1870),Emden(1907).The polytropic index is zero and the pressure and density correspond to a constant, and the other analytical and numerical solutions exist for n=1,1.5,2,3,4 and also for 5.Hence,the n ≥5 solution contains infinite mass with the range of 0 <n <5 for the polytropic model.Each colored line shows a different polytropic index in Figure 10.
5.Conclusions
The reason for the W UMa type CBs exhibiting long-term evolution is because the W UMa type CBs are known as low mass stars.We have derived the basic evolution equations of mass transfer between the components of W UMa type CBs and we calculated the orbital and stellar parameters for these selected systems from the W UMa type CBs.
We have presented the evolution of AML and effect of mass transfer in the subclasses of W UMa type CBs based on the catalogs of Yildiz(2014)and Sun et al.(2020).We determined the stability of stars based on the effect of mass transfer in the parameters of Roche lobe radius of the donor stars and critical mass ratio of W UMa systems.
In this study, we have calculated some stellar and orbital parameters,which are not yet calculated in the catalog of Yildiz(2014) and Sun et al.(2020); some of them were critical mass ratio,Roche lobe radius of the donor star,mass ratio,AML and orbital angular velocity of the stars of the W UMa type CBs.We calculated the combined and color temperature based on the late-type W UMa CB catalog of Sun et al.(2020).These two parameters used to explain the color of stars are based on the temperature whether they are blue, red, yellow, orange or other colors.
We explain the internal stellar structure of W UMa type CBs using a polytropic model.In the polytropic model, different numbers of indexes are used to explain the internal stellar structure of the donor stars and the relation between the physical parameters of W UMa type CBs with stable mass transfer (Lane 1870;Emden 1907;Sirotkin & Kim 2009).The final results are presented in Tables 2 and 3.

Table 2 The Observed and Calculated Parameters for A- and W-type W UMa CBs Using Md ≥0.7 M⊙(Yildiz 2014)

Table 3 The Observed and Calculated Parameters for A-, B- and W-type Late-type W UMa CBs Using Md ≥0.7 M⊙(Sun et al.2020)
Acknowledgments
We thank the Space Science and Geospatial Institute(SSGI)-Entoto Observatory and Research Center (EORC) Astronomy and Astrophysics Department for supporting this research.This research has made use of NASA’s Astrophysical Data System.
 Research in Astronomy and Astrophysics2023年4期
Research in Astronomy and Astrophysics2023年4期
- Research in Astronomy and Astrophysics的其它文章
- Study of Central Intensity Ratio of Seyfert Galaxies in Nearby Universe
- The Variability and Radial Velocity of Planetary Nebula Central Stars
- Period Investigation on Two W UMa Binaries HH UMa and V1175 Her
- 3D Kinematics of Classical Cepheids According to GaiaEDR3 Catalog
- Constraining the Temperature-density Relation of the Inter-galactic Medium from Analytically Modeling Lyα Forest Absorbers
- Influence of Solar Activity on Precise Orbit Prediction of LEO Satellites
