单相桥式全控整流与单相半波可控整流电路的对比研究

罗月芳 柏泽龙 李吉成 孙坤鹏

（云南工商学院智能科学与工程学院 云南省昆明市 650500）

近年来，电力电子整流技术广泛应用于民用及工业领域。小到家用电视、手机电脑充电器，电加热水壶等直流加热设备，大到新能源汽车充电桩及高铁牵引变流器，电力电子整流电路已经深入到生产生活方方面面。在国家倡导的减碳发展之路上也将发挥更重要的作用。

单相桥式全控整流电路与单相半波可控整流电路是整流电路中的基础电路，对该两种电路的输出及输入的对比研究可以更好的理解两种电路的特性，对电网及负载的影响等。

1 单相半波可控整流电路

1.1 电路组成

如图1 所示，为单相半波带阻感负载有续流二极管的可控整流电路拓扑图，电路中主要包括一个晶闸管VT，一个二极管VD。负载采用纯阻性负载R，同时预设置一个电感元件L 以保证输出电流的连续性。

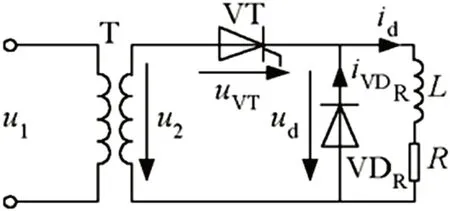
图1：带续流二极管的单相半波可控整流电路

1.2 工作原理

从图1 可以看出：晶闸管VT 与二极管VD 为全电路系统的核心结构，当VT 在（2kπ+α）角度导通的情况下，晶闸管VT 导通，导通角为（2kπ+α）至（2kπ+π），导通时长为（π-α）。待角度至（2kπ+π）时，晶闸管断开，此时输入端电流为0，而负载端二极管VD 导通，电感L 续流效应使输出保持，电流连续，二极管VD 导通时长为（π+α）。待到运行至下个周期时，晶闸管及二极管导通重复上述过程。负载输出电流则处于连续输出状态。

1.3 MATLAB模型建立

考虑到本次仿真主要通过对比相桥式全控整流电路与单相半波可控整流电路的输入输出波形对比，故预设输入电压为国网工频额定电压即：电压AC220V，工频f=50Hz。而输出电压采用DC48V，负载采用0.5Ω 电阻。则可算出输出电流Id 为：

当VT 处于导通状态时，根据电压关系可得到公式如下：

其中C 为常数。当VT 导通瞬间其电流为：

当VT 断开时，电流瞬时值表述如下：

考虑到电路工作稳定后，理想电感仅为能量转换器件，在晶闸管导通时充电。在晶闸管断开时向电阻放电。则可认为带反并联二极管电路电流有效值与负载为纯电阻的电路电流有效值相等。建立公式有：

计算得：

将式（7）带入式（3）可得：

对式（8）中ωt求在[α,π]中最大值，可得：

电路电流平均值为：

2 单相桥式全控整流电路

2.1 电路组成

如图2 所示，为单相桥式全控整流电路拓扑图，电路中主要包括一阻桥式电路。负载采用纯阻性负载R，同时预设置一个电感元件L 以保证输出电流的连续性。

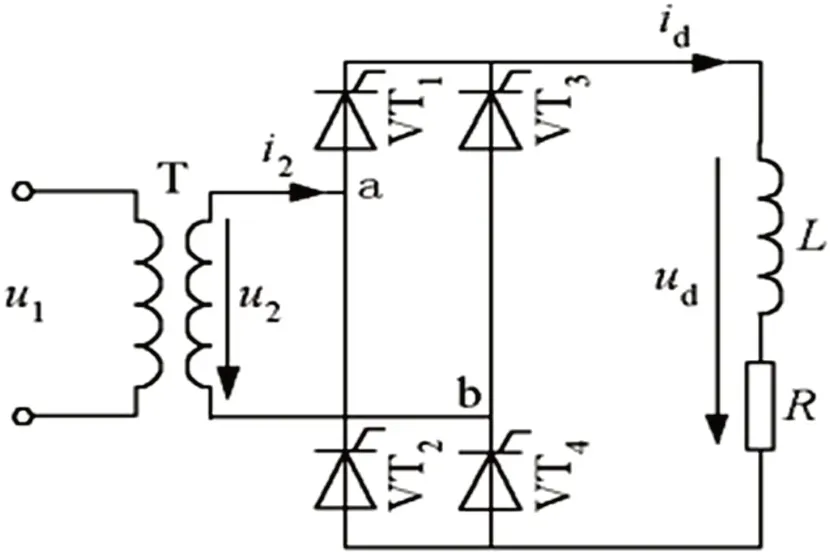
图2：单相桥式全控整流电路

2.2 工作原理

从图2 可以看出：桥式为电路系统的核心结构，当VT1 与VT4 在（2kπ+α）角度导通的情况下，晶闸管VT 导通，导通角为（2kπ+α）至（2kπ+π+α），导通时长为π。待角度至（2kπ+π）时，因VT2 与VT3 导通，VT1 与VT4 截止，此时输入端电流为0，电感L 续流效应使输入电压U2即使为负也可仍然工作，电流连续，同理在后半个周期VT2 与VT3 以同样的工作方式进行工作。

2.3 MATLAB模型建立

考虑到本次仿真主要通过对比相桥式全控整流电路与单相半波可控整流电路的输入输出波形对比，故预设输入电压为国网工频额定电压即：电压AC220V，工频f=50Hz。而输出电压采用DC48V，负载采用0.5Ω 电阻。则可算出输出电流Id 为：

当VT1 与VT4 处于导通状态时，根据电压关系可得到公式如下：

其中C 为常数。

考虑到电路工作稳定后，理想电感仅为能量转换器件，在晶闸管导通时充电。当电路运行在负向周期放电。则可认为带反并联二极管电路电流有效值与负载为纯电阻的电路电流有效值相等。建立公式有：

计算得：

将式（15）带入式（13）可得：

对式（16）中ωt求在[α,π+α]中最大值，可得：

电路电流平均值为：

3 计算结果对比

单相桥式可控整流电路通过桥结构可利用负半周期波形作为输出，故其电压利用率高输出电压为单相半波可控整流电路输出的一倍，故经计算：单相桥式电路电流输出而单相半波可控整流电路电流输出为

仿真环境按照输入交流10V/50Hz，输出负载为电阻为0.5Ω，电感为0.04H，控制角α 为30°设置。仿真模型搭建如图3 和图4 所示。

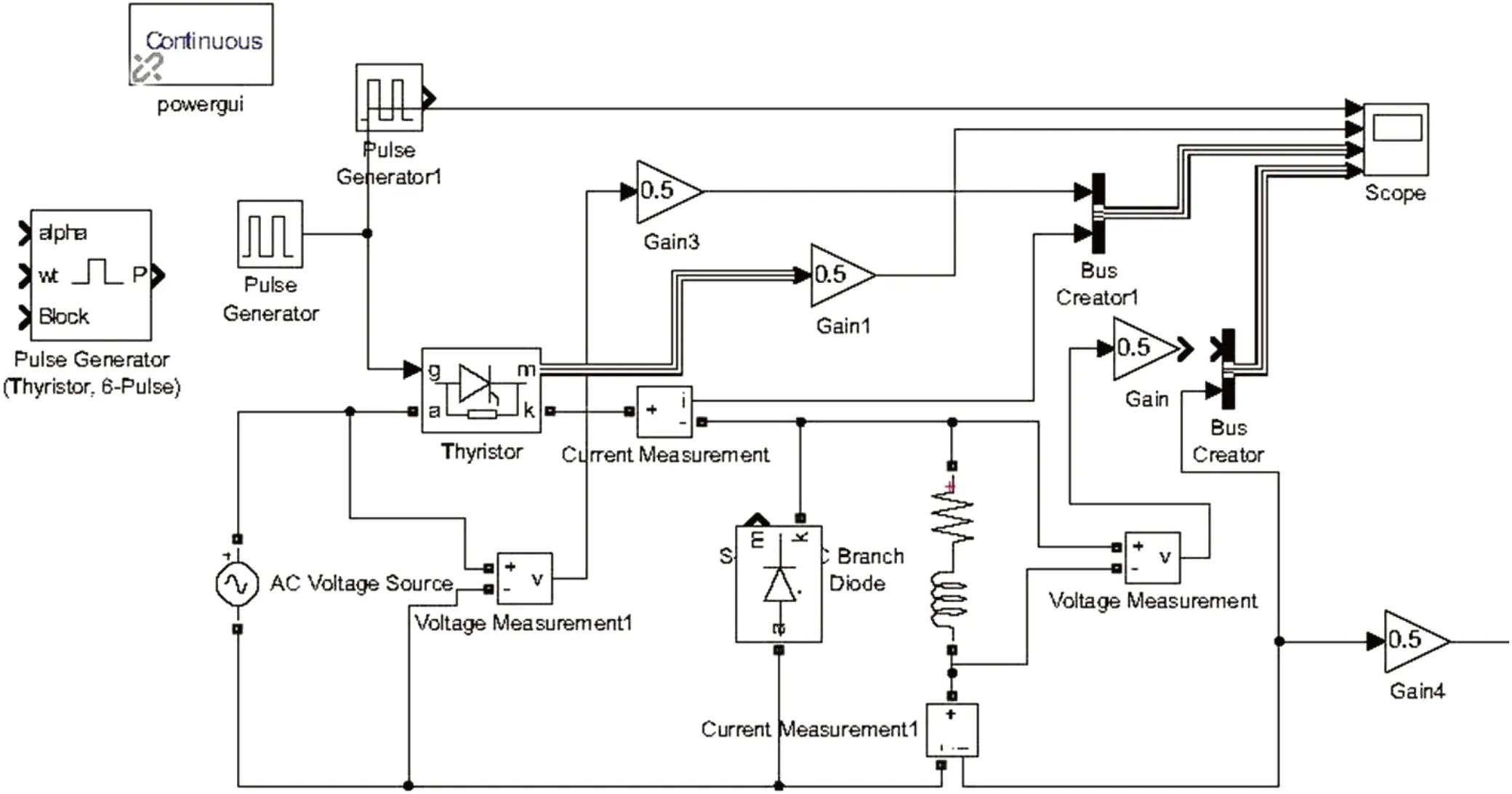
图3：带续流二极管负载为感阻的半波可控整流

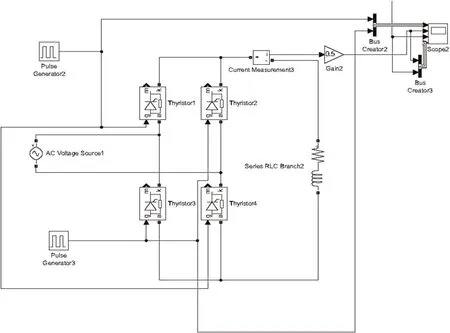
图4：单相桥式可控整流电路

而在波动性上由式（17）及式（9）对比可知：桥式可控整流电路的稳定性比半波可控整流电路要略低，原因为当桥式电路工作在负向周期时，电感的波形变化更剧烈。具体仿真结果如图5。

图5：单相桥式可控整流电路及带续流二极管负载为感阻的半波可控整流电路仿真结果

4 结论

本文在对单相桥式可控整流电路和半波可控整流电路理论分析的基础上，建立了基于MATLAB/Simulink仿真的单相桥式全控整流与单相半波可控整流电路的仿真模型，并对其进行了分析研究。通过仿真得出整流电路的输出波形波动情况除受输入电压波形利用率影响外，电感的工况对输出电压仍有很大的影响，可通过增大电感取值或调整整流电路来实现输出的稳定。因此，在实际应用中若对输出波形要求较高时，可调整电感的取值来减小波动的范围。