风力发电塔筒在地震和风载下的失效分析

徐 凯，张锦刚，李周波，王和平，马 璇 编译

（1.中油国家石油天然气管材工程技术研究中心有限公司，西安710018；2.宝鸡石油钢管有限责任公司，陕西 宝鸡721008）

0 前 言

如今，风能虽然存在一些争议，但是它仍被作为一种可再生能源广泛使用。一项研究表明，全球公用事业规模可再生能源发电设施的装机容量在2022 年创下22 000 万kW 的历史新高，而光伏和风能投资总和超过3 000 亿美元。到2030 年，全球风能行业可能会新增近10 亿kW 装机容量。风力发电机塔筒的设计通常采用的标准有IEC 61400 （IEC 2005）和GL（2010），在北欧的风能开发基础上建立的相关技术已被世界各地的许多地区采用。然而，如热带气旋或地震这种极端载荷条件在亚洲地区更为常见，在中国东南沿海地区，极端的台风造成的风电塔筒失效时常见诸报端。虽然受地震造成的塔筒失效很少见，但地震的风险应当受到重视，因为风电场中的风机塔筒通常采用相似的设计并且没有冗余，而地震则会对风电场中所有塔筒造成冲击。

本研究对风电塔筒在风和地震作用下的综合性能进行分析研究，用到的方法包括试验测试、现场调查和数值分析。塔筒在大规模动力激励下的失效试验往往受到试验场地空间和安全性的限制而难以开展。虽然已经开展过一些大规模的弹性试验，如Prowell 等人在2009—2014 年对停用的塔筒进行了大规模试验，但几乎没有开展过塔筒的失效试验。此外，Treuren 在2015 年提出塔筒在风洞试验测试中的尺度问题，可能会影响试验结果的准确性。灾难发生后对故障塔筒开展调查可以提供有实用价值的现场信息，但这些都是极端事件的最终阶段结果，无法具体描述塔筒失效的过程。合理使用基于非线性有限元（FE）分析的数值模拟技术，能够模拟计算出塔筒在极端载荷下的失效过程。

关于塔筒在地震响应下的数值研究，Nuta等在2011 年用有限元法对其进行了增量动力分析（IDA），并获得塔筒的易损性曲线。之后，Patil等人在2016 年对塔筒在近断层地震和远断层地震影响下进行了详细的易损性分析。2017 年，Sadowski 等将塔筒的IDA 结果与近断层地震和远断层地震下的焊接缺陷进行了比较。关于塔筒在极端风力载荷下的数值研究，2014 年，Zhang 等模拟了在台风风速下塔筒的动态响应，进一步研究塔筒在风载下的失效模式。Dai等在2017年对一座典型的1.5 MW风电塔筒进行了有限元分析，并注意到了不同风向下风力载荷导致的塔筒倒塌的不同失效阶段。此外，还有很多学者研究了塔筒在多种危险载荷下的结构性能：Asareh等通过有限元分析研究了塔筒在风力载荷下的地震易损性分析；Smith 和Mahmoud 评估了不同高度的风电塔筒在风载荷、运行载荷和地震载荷下的综合性能；Mo 等考虑到塔筒不同的服役条件，对其进行了地震易损性分析。综上所述，尽管有许多研究已经使用了非线性动力有限元方法对塔筒进行模拟计算，但很少有专门比较强地震或风作用下塔筒的失效过程。

本研究针对风电用典型塔筒在风和地震综合作用下的非线性响应进行了分析。虽然长期的横风效应（如涡激振动）可能会导致塔筒的结构损坏，但本研究更侧重于极端载荷工况下的响应分析，因此仅考虑顺风载荷效应。首先介绍了塔筒有限元建模过程，然后介绍了相应的地震和风载激励，重点进行了风载荷和地震载荷下塔筒响应的动力分析和非线性静力学分析，以指出载荷频率、结构振动模式和主要倒塌机制之间的关系。

1 有限元模型和模态分析

1.1 有限元模型

本研究模型选择了中国东南沿海广泛建造的典型1.5 MW 三叶水平轴风电塔筒，如图1（a）所示。根据IEC 61400（IEC 2005）标准将其定为IIa 级（叶片高度处的10 min 参考平均风速为42.5 m/s，湍流强度为0.16），但并没有明确考虑其抗震性能。该塔筒是一根近乎圆柱形的中空钢管，具体参数为：34 m的高度内其外径约为4 035 mm，然后在34 m 以上外径从4 035 mm 线性减小到2 955 mm；塔筒厚度分别为10～25 mm；叶片距离底座63.209 m，塔筒质量约为91 t，叶片直径约为70 m；塔筒顶部叶片和风机舱质量分别为30 t 和60 t。通常在极端条件下会使用制动索具将叶片调整至停车状态（即转子转速保持为零，发电机不工作），以减少潜在的转子运动。因此，本研究对塔筒在停车状态下进行了研究。

图1 1.5 MW典型风电塔筒实物照片及有限元模型

该塔筒有限元模型如图1（b）所示。塔筒壁采用的单元是线性缩减积分有限应变S4R三维（3D）壳单元，该单元适用于动态和静态分析。使用四面体扫描网格技术对每个筒壁段进行网格划分，由于每个筒段连接处应力场比较复杂，因此在这些区域尽量增大网格密度，以提高计算准确性。此外，在建立模型时，在塔壁上建立椭圆形切口用来模拟塔筒底部的门，并且根据实际设计，在位于底部上方13.4 m、34.2 m 和61.8 m 处用加强法兰以增加塔筒截面弯曲刚度。为简化计算，忽略了螺钉和螺孔，加强法兰选取三维壳单元，从顶部到底部的三个法兰（1～3）厚度分别为80 mm、220 mm 和220 mm，分别从塔壁延伸96.5 mm、133.5 mm 和137 mm。在有限元模型中，电机舱和叶片简化为两个集中质量动力耦合。因为重点研究的是在停车条件下塔筒的结构响应，因此，这样的简化建模方式是合适的。塔筒的地基建模设定为完全刚性约束，即没有位移和旋转。最后，本次计算暂时不考虑塔筒结构与土壤的相互耦合作用。

模型选取的材料为S355 钢，并设置为弹塑性材料，屈服后应变硬化（0.1%）。屈服应力355 MPa，泊松比为0.3，弹性模量为200 GPa，密度为7 850 kg/m3。此外，在整个有限元模型中定义了整个塔筒的自接触规则，用来表征结构在大变形下不同壁段表面之间的潜在接触。根据目前的研究结果，在地震作用下，1.5 MW风力发电机停车状态选取1%的阻尼比。在本次分析中，结构阻尼是通过基于一阶模态和二阶模态的瑞利阻尼引入的。本研究表明这两种频率在结构响应中处于主导地位，这也验证了该阻尼形式的合理性。

1.2 模态分析

利用有限元计算得到了塔筒整体弯曲的前三阶振动模态（见表1）。从表1可以看到，两个水平方向（x和z）的振动模态非常接近。数值结果与之前对塔筒进行的现场测量所获得的结果以及之前对同一模型进行计算分析获得的数值结果之间也保持着良好的一致性，表明本次计算得到的模态分析是准确的。

表1 塔筒的前三阶整体弯曲振动模态

2 动态响应

之前关于塔筒在地震响应的研究是根据设计谱、断层距离和脉冲效应对地震波进行分类的。然而，在选择的过程中并没有直接考虑地震波的频率。风电塔筒通常具有相对较低的固有频率（一般在0.5 Hz 及以下，见表1），本研究目标是研究不同频率的地震波如何引发塔筒不同的动力学结构响应和失效模式。研究根据中国地震标准GB 50011—2010 建筑抗震设计规范中给出的5%阻尼设计反应谱，从太平洋地震工程研究中心的强地震数据库中筛选了地震记录。此外，该设计反应谱的最大谱加速度为0.5g，这是根据拟建塔筒选址确定的。

本研究选择了两组具有不同土壤特征周期（Tg）的地震波。特征周期代表响应谱中恒定速度和恒定加速度的转变点。值得注意的是，在选择地震波时，没有考虑地震的剪切波速。本研究总共选择了20 条地震的记录，包括对应于硬土条件（简称ST）下10 条Tg=0.4 s 的记录，以及对应于软土（简称LT）10 条Tg=1.1 s的记录。近断层地震具有明显的潜在破坏性特征，如向前方向性、滑冲效应和上盘效应。其中一部分还包含了塔筒比较敏感的速度脉冲。因此，本研究只选取破裂距离小于20 km的近断层地震。图2 为目标加速度响应谱和两组地震记录的反应谱，这些反应谱是由前面提到的10 个地震记录的两个水平分量的平方和开方根得到的。图2 还包括了每组地震波的平均谱，由10 个单独响应谱的算术平均根获得。此外，图中包括塔筒的前两阶自震周期。虽然表1 中一阶模态的有效质量比大于二阶模态，但二阶模态的加速度要高得多，这表明塔筒的结构响应也会受到二阶模态的显著影响。

图2 地震波加速度响应谱及结构前两阶振动模态

在有限元模型中，在塔底施加水平方向加速度。由于地震波的垂直分量对塔筒的响应影响不大，因此未考虑地震波的垂直分量。此外，为了反映塔筒的弹塑性性能，将所有地震波的地面加速度峰值（PGA）缩放到了四个级别，分别为0.1g、1g、2g和3g。

3 风载的影响

本研究采用CDRFG 方法模拟了强风速场，这样可以在保证对应的时空前提下，在塔筒的不同点生成与目标风速功率谱一致的风速。为了对塔筒进行非线性响应的失效分析，本研究选取三个风速级别，在轮毂处的平均风速分别为Uref=50 m/s、55 m/s 或60 m/s。其中，风载的生成基于谐波的总和，频率间隔为0.2 Hz，下限和上限分别为0.01 Hz 和10 Hz。生成的载荷持续时间为600 s，时间间隔为0.1 s。表2 列出了与风场模拟相关的其余参数。参考10 min 平均风速，总共生成了三个独立的风速场，来研究塔筒结构响应的变化。

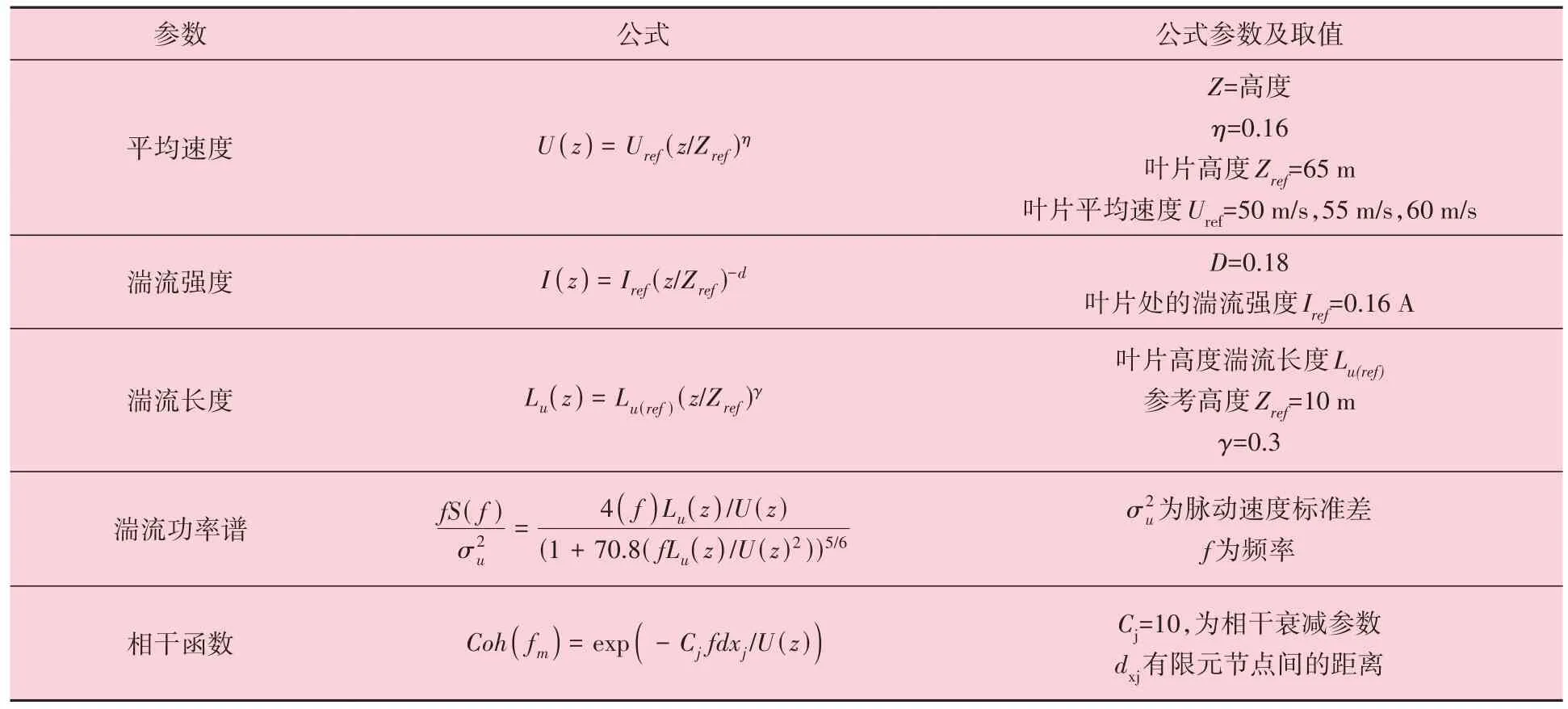
表2 风载计算中使用的参数

使用叶片单元动量（BEM）理论计算叶片上的载荷。每个叶片沿其长度方向划分成17 个单元。叶片受到风的推力、切向力、升力和阻力，升力和阻力取决于风的瞬时迎角。叶片施加在塔顶的总力是这些单元载荷的总和。

塔身和风舱上的风载荷时程为

式中：ρ——空气密度，ρ=1.25 kg/m3；

U2（t）——瞬时风速时程，m；

Cd——阻力系数，塔筒系数为1.2，风舱系数为1.3；

A——投影面积，m2。

在诸如热带气旋的极端情况下，塔筒通常处于停车状态，叶片处于“羽毛”状态，这样可以减少前后方向的风载荷。然而，由于这种极端条件下风向快速变化，风速可能平行于塔筒的侧向（即有限元模型中的z方向），此时风力对塔筒的影响非常显著，因此，本研究中风向设定为侧风。

4 失效分析与讨论

4.1 弹性结构响应

本研究对塔筒的结构响应计算从其弹性范围内开始，这样可以清楚地了解不同震动模态对结构的影响。为此，计算中使用了0.1g PGA 的地震波，塔筒在计算中保持完全弹性。

从有限元模型中提取了塔顶相对水平位移和底部弯矩的时程响应。对两个水平方向的时程结果使用SRSS 方法进行组合得到每个地震的结果，并计算了ST 地震和LT 地震的算术平均值、均方根（RMS）和峰值响应（表3）。

表3 塔筒对0.1g PGA为地震的响应

结果表明，塔筒在弹性范围内受LT 地震影响较大。出现这一结果的原因是，如图2 所示，在相同PGA 下LT地震与ST地震记录比较，在基本振动周期内，有着更大的加速度。

针对两次具有代表性的ST 地震和LT 地震，研究了前两阶模态中塔筒位移最大截面处的加速度。这两个截面分别与图1 中的A1 点和A2 点相对应，分别位于距离塔底部61.8 m和39.8 m 的高度处。同时还研究了轮毂处平均速度为50 m/s 风场中这两个截面处的加速度。对两个水平方向（x和z）的加速度分量进行处理，通过SRSS 方法获得其能量谱密度（PSD），并根据基频处的峰值对能量谱密度进行归一化处理。图3 分别显示了A1和A2塔段的归一化PSD 曲线和前两阶模态的振型。图3（a）显示，塔顶（A1）的响应明显受基本模态控制；然而，图3 （b）显示，中间部分（A2）受二阶模态控制。对于ST 地震，二阶模态对塔筒中间区域的响应控制尤为明显。这是由于ST 地震中，二阶模态具有相对较大的加速度（图2（a）），而且二阶模态在模态位移中也占主导地位。以上结果表明，根据前两阶模态就可以确定塔筒上半部分弹性结构响应。当结构承受风载荷时，无论塔筒上半部分的位置如何，响应始终由其基本模态控制，这是因为风载在低频振动区域能量更大。

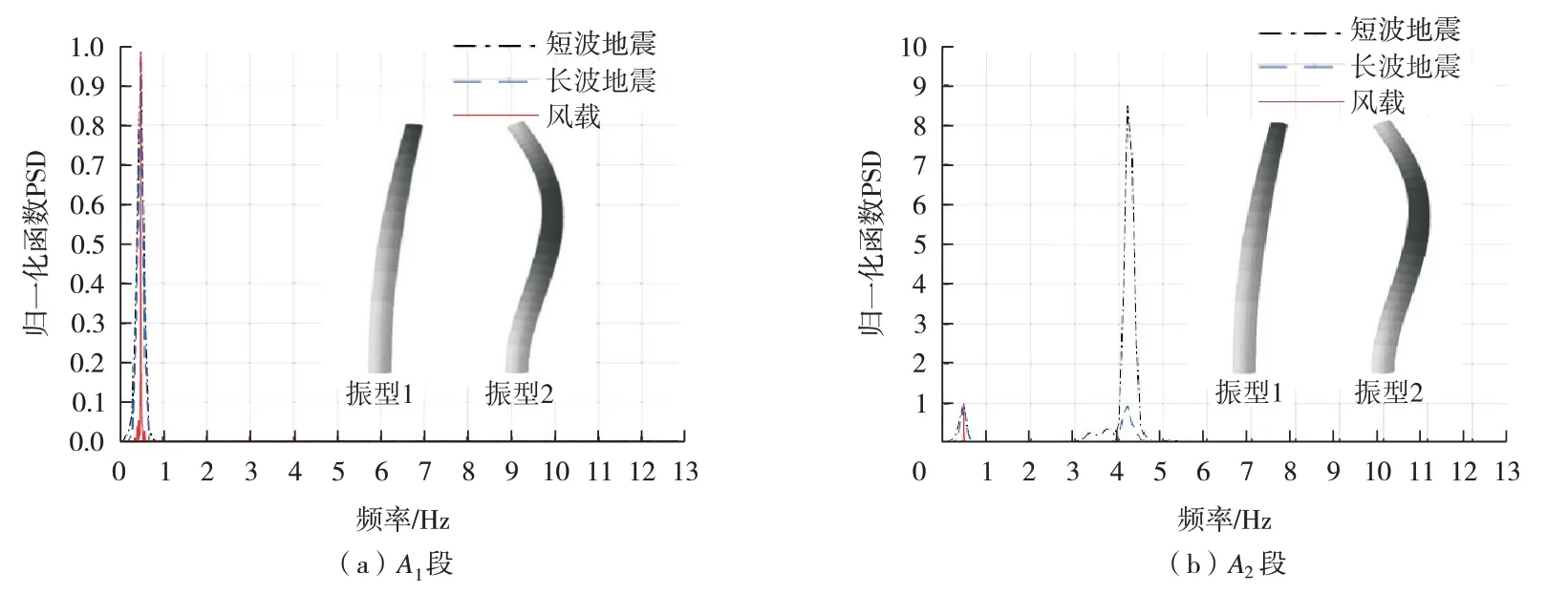
图3 地震响应下（PGA=0.1g）或风载荷（Uref=50 m/s）下A1段和A2段的加速度PSD

4.2 强地震作用或风载荷下的典型失效模式

对3 个PGA 水平（1g、2g 和3g）下的20 条地震和3 个速度水平（50 m/s、55 m/s 和60 m/s）下的风速场进行了一系列非线性动力学有限元分析。使用Hilber-Hughes-Taylor 时间积分和自动增量歩求解非线性时程计算。在非线性动态响应分析中发现了四种不同的失效模式，如图4～图7 所示。而且失效过程可分为四个阶段：第一阶段，初始塑性铰形成；第二阶段，塑性铰发展；第三阶段，形成全截面塑性铰；第四阶段，结构局部屈曲。图4～图7云图表示出了塔筒的失效过程，并用t1、t2、t3和t4确定了四个阶段，图中1（黑色）表示结构的屈服。

图4 第一种短波地震下的失效模式（PGA=2g）

图5 第二种短波地震下的失效模式（PGA=3g）

图6 第三种长波地震下的失效模式（PGA=3 g）

图7 风载下的失效模式（Uref=55 m/s）

塔筒在地震或风载作用下的失效过程中，塑性铰从塔筒的底部开始发展，然而，随着外部激励能量的增加，损伤向塔顶扩散，并在焊接处发生屈服，因为组成塔筒的圆环在焊接处厚度会发生变化，这种厚度的变化会导致应力集中，从而形成塑性铰。当塔筒在某处沿着其整个周向屈服，就形成一个完整的塑性铰。此时，塔筒结构开始失效，塑性铰上方的部分几乎可以自由旋转。无论在哪种载荷类型下，由于塔筒的结构冗余度较低，一旦出现全截面塑性铰，塔筒会在短时间内失效。

研究中发现，在不同的地震波影响下，全截面塑性铰可能出现在塔筒四个不同的位置。然而，风载荷影响下，全截面塑性铰则总是出现在底座上方8.8 m的固定位置。由于不同作用下塔筒破坏位置的变化，因此对基于残余变形的传统失效指标CDR进行修正以考虑不同的失效高度的影响为

式中：Dt——塔顶位移，m；

Ht——塔高，m；

Hc——失效发生的高度，m。

本研究还计算了Camara 等人提出的ω比，用来研究分析塔筒在不同位置的塑性耗能。ω比的定义为累积塑性耗散能量除以输入的总能量。整个塔筒的CDR和ω比的变化如图4～图7 所示。很明显，在塑性铰的发展阶段（阶段2），这两个指数都显著增加。在图中用垂直的虚线标记时间历程响应的两个分界点，这两个值会在失效模式数据中进行处理：①t3是形成全截面塑性铰的时刻；②t4为CDR达到0.1 的时刻。可以看出，全塑性铰的位置越低，塔筒钢材滞回吸收的塑性能量越高，因此ω比越大。在图4 中，ω比在t3和t4时分别为10%和32%，这是由于塑性铰的位置相对较高，结构吸收地震能量的能力有限，在倒塌发生前其耗散地震能量能力较低，这样的失效被认为是脆弱且不理想的。图5中塔筒底部塑性铰的破坏模式与图4中观察到的破坏模式截然不同，其塑性铰位于塔架底部（基座上方5.9 m），因此，倒塌前塑性吸收了高达76%的地震能量，塔筒底部的耗散能力较大是因为该区域的墙体半径和厚度均较大。

从失效持续时间（t4～t3）的角度来看，中上部破坏对应的耗散能力较低，全塑性铰发展较快（图4 中，失效开始到CDR=0.1 仅需0.5 s）。这与塔底部出现全塑性铰的失效情况形成对比（图5 和图7 中，失效开始到CDR=0.1 分别为25 s 和10 s）。

5 失效模式统计

通过研究非线性时程地震和风载荷分析中塔筒的失效位置，表明LT 地震更容易诱发局部屈服（阶段1 和2）和全截面塑性铰发展与屈曲塑性铰失败（阶段3 和图4），这是由于LT 地震在基本模态中有更高的谱加速度,正如前面所讨论的那样。

图4～图7所示所有的局部屈曲失效都发生在塔筒壁厚变化的位置，即在基地5.9 m 以上基地（9%的总高度，厚度变化从25～19 mm），8.8 m（14%高度，厚度变化从19～18 mm），25.4 m（高39%，厚度变化范围为14～13 mm），39.9 m（61%高度，厚度变化为11～10 mm）。结果表明，塔筒厚度的变化在动力作用下会产生应力集中，更容易形成全塑性铰。

图8 所示为全截面塑性铰发生时和CDR=0.1时ω比的对比图。纵坐标表示塔筒失效位置的高度，横坐标表示相应的ω比。除5.9 m 高度的失效外，结果与“强地震作用或风载荷下的典型失效模式”中讨论结果的一致。该位置的平均ω比低于8.8 m 和25.4 m 处的，这可能是由于5.9 m 处的厚度变化较大（6 mm）。总体趋势是，随着失效高度的增加，塑性耗散能量的ω比减小。

图8 全截面塑性铰发生时和CDR=0.1时ω比的对比图

研究发现，失效通常发生在塔筒的下半部分。在33%的ST地震中失效发生在塔筒中上段，这一比例高于ST 地震的17%。由于靠近塔底的塑性铰ω比值较大，LT 地震动作用下结构耗散的地震能量要大于ST 地震动作用下结构耗散的地震能量。与地震载荷相比，塔筒在强风作用下总是在底部位置发生失效，距地面高度8.8 m处。相应的，在风载作用下塔筒的塑性耗散较大。

5.1 非线性静力学分析

在不同的外载作用下，不同频率的振动导致了失效模式的变化。为了进一步探索外载频率对失效的影响，本研究又进行了非线性静力（pushover）分析。之前对塔筒的非线性分析往往只考虑了低阶模态对载荷的影响，或者是直接在塔筒顶部施加单点载荷或位移。然而，正如本研究进行的非线性时程分析所示，在地震载荷（尤其是ST地震）下高阶模态的影响也是非常大的，因此，本研究基于前两阶模态，进行了模态非线性静力分析。对于每个振动模态，有限元模型第i个单元处的载荷为

式中：mi——第i个单元的质量，g；

φi——第i个单元的模态位移，m。

除了探索地震波下塔筒的响应而进行的模态非线性静力分析外，本研究还进行了沿塔筒高度的平均风载影响下的模态非线性静力分析，用来研究风载下的塔筒失效。其中，截面平均风速和获得风载的方法在“风载的影响”一节中已经进行了阐述。

在塔筒的静力模态推覆分析中，风载逐渐增加，直至塔筒发生失效，如图9 所示。在与一阶模态和二阶模态载荷模式对应的情况下，塔筒结构在离地高度分别为8.8 m 和42.8 m 的横截面处发生失效，其失效模式与动力学响应分析基本保持一致。在二阶模态下，塔筒的失效位置稍微偏上。这与动力响应分析中的结果也是一致的，这种情况在短波地震中的影响更为明显。在截面平均速度风载下，塔筒由于在结构底部（距基座5.9 m）形成塑性铰而发生失效。

图9 关联前两阶模态和风载下塔筒的弹塑性计算结果

5.2 地震和风载作用下的响应频率

本研究选取了影响塔筒不同位置失效的3类ST 地震、LT 地震，比较了3 种情况下的加速度，对其峰值进行了归一化处理，如图10 所示。为了更好地进行比较，还进行了叶片高度处风载的归一化PSD（Uref=50 m/s）。由计算结果可以看出，一方面由于地震波的频率范围很广，导致了塔筒更多的高阶模态；另一方面，风载有更多的频率与塔筒的基本频率相近，更容易引起塔筒的共振失效。

图10 3种地震波和风载频率的归一化PSD

进一步分析可知，横向风载荷的频率对塔筒的失效有显著影响。第一种地震主要以低频为主，会导致塔筒在底部区域出现失效。然而，第二种地震包含了二阶模态，其整个频率范围内具有较大的PSD值，这就会导致塔筒结构中上部区域发生失效（图4 所示）。与前两者相比，第三种LT 地震具有更宽的频率范围，因此在这种情况下塔筒的失效发生在结构的中低区域（图6所示）。

综上所述，对于ST 地震，在考虑塔筒模态的情况下，其归一化PSD 值比LT 地震和风载激励更大，而LT 地震和风载激励往往会使塔筒失效的位置向上移动。由于地震波的不同与变化，会产生不同的激励载荷，因此最终导致塔筒的失效位置发生变化。最后，风载频率与塔筒结构本身如果发生频率共振则会导致塔筒本身发生失效甚至倒塌，这也可以为后续塔筒的结构设计提供参考。

6 结论及建议

本研究建立了详细的风电塔筒有限元模型，对其在极端载荷（地震和风载）下进行了相关的有限元计算与分析研究。选择了两组具有不同频率的地震波，并生成了一系列风速时程，共进行了89 次非线性动力分析，同时进行了非线性静力（pushover）分析，得出以下结论：

（1）由于考虑塔筒振动模态在结构响应中的影响，以长波为主的地震比短波地震对塔筒的结构影响更大。

（2）在横向风载下，塔筒结构的失效始于结构底部，并且随着载荷的不断增加，结构损伤会集中在塔筒中焊接处，此时其壁厚会发生变化，一旦一个部分发生屈服，就会形成一个全塑性铰链，塔筒就会发生失效甚至倒塌。

（3）全截面塑性铰的位置取决于激励的频率范围，风载和大多数的长波地震会激发结构的一阶模态，导致塔筒的下半部分发生失效。然而，由于二阶模态的影响，短波地震更有可能在塔架上部形成塑性铰，导致塔筒中部或上部发生失效，如果塔筒具有相对较低的能量耗散能力则会快速发生倒塌。

（4）非线性静力学分析可得到塔筒在相应激励下的共振频率，为其潜在的失效危险提供参考，与高阶振动模态相关的载荷会使塔筒在中部或上部区域发生失效。

在实际的塔筒设计和使用中，为改善极端载荷下塔筒的结构性能，建议注意以下情况：

（1）在进行塔筒设计时，应特别注意位于地震风险可能激发高模态的响应。例如，短波地震下塔筒约60 m 的高度区域。建议在中部和上部增加塔筒壁厚，充分耗散能量以便于塑性铰的发展尽可能接近塔筒底部。

（2）对于强风条件，结构底部更容易受到影响。建议对位于强风载荷主导位置的风机下半部分进行加固。

（3）在塔筒的设计中应避免厚度的急剧变化，这样可以最大限度地减少塑性下降，将塔筒突然倒塌的风险降至最低。

上述结论与建议只是基于本例中塔筒分析得到的，为了更全面深入地研究，还需要对不同动态特性的其他塔筒进行更多的分析研究。此外，考虑土-结构耦合作用以及风-地震耦合下的非线性响应，也需要进一步计算分析。