针对车辆路径问题的专利分析

赵文华 吴雪

摘要 车辆路径问题是调度管理和运输组织优化中的核心问题，也属于运筹学中的一种组合优化问题，旨在构造合适的车辆行驶路线从而实现运输成本的最优化。文章介绍了路径规划问题的常见种类以及多种算法，总结了上述算法的研究现状，以及研究中还存在的问题，并利用专利分析系统对各个算法下的相关专利进行统计分析，便于对各个方法的研究热度进行讨论，以期对今后车辆路径问题方面的专利申请给予参考和指引。

关键词 车辆路径问题；算法；专利；物流；运输；配送

中图分类号 U116.2文献标识码 A文章编号 2096-8949（2023）09-0183-03

0 引言

车辆路径问题（Vehicle Routing Program，VRP）最早来源于Dantzig和Ramser于1959年发表在《Management Science》上的文章《The Truck Dispatching Problem》。该问题起源于交通运输，涉及查找一组路线，这些路线共同覆盖一组客户，每个客户都有给定的需求，目标是最大限度地减少总行驶距离或使用的车辆数量，或这些的组合[1]。路径规划问题是现实生活中普遍存在的，且根据实际约束条件的不同，可以抽象出VRP问题的不同种类，例如，带容量限制的车辆路径问题（CVRP）（Kallehauge et al. 2006）。近年来，有时间约束限制的派送服务急剧增长，这种服务中访问的客户可能要求在某个时间点前完成派送等，即一种带时间窗的车辆路径问题（VRPTW）。早期有关解决带时间窗口路径问题的研究可参考（Desrochers et al. 1988）和（Solomon and Desrosiers，1988）。日常生活中有随机需求的收送服务，需要根据不同时段中随机出现的需求服务的客户点进行路径规划。上述VRP的种类中，又各自分为路径在一个或多个配送中心（depot）两种情况，也涉及同类车型或不同车型的问题。

1 VRP的常用算法

车辆路径问题的一般求解方式是根据优化目标结合一个或多个约束条件进行建模，然后基于构建的数学模型选择合适的算法，从而获得该问题的最优解或次优解。在解决上述路径问题时，通常会用到精确算法和启发式算法。在算法方面，国内外的很多学者都进行了深入研究，20世纪60年代集中在各种形式的节约算法，到70—80年代又提出了多种基于数学规划的算法，80年后期至今又涌现出各种智能算法[2]。

1.1 精确算法

VRP问题中常用的精确算法有：动态规划，列生成，分支定界，分支切割，拉格朗日松弛算法等。Desrochers et al.（1992）用列生成算法解决了Solomon的100个访问节点的问题；Pecin等提出了分支定价割平面算法（Branch Price and Cut）来求解带时间窗的VRP，减少了计算复杂度，从而加快了算法求解速度[3]。ZHAO[4]通过列生成算法和动态规划算法实现了对循环式带访问频率的多车辆路径问题的解决。胡剑鹏等针对柔性时间窗的电动车车辆路径问题建立了以配送成本最小为目标的混合整数规划模型，利用列生成算法进行求解，将模型转换化为有资源约束的最短路径子问题。这类算法适用于规模较小、结构简单的情况，能够获得问题的最优解，但是随着客户点的增加，算法复杂度呈指数级增加，普遍耗时较长[5]。

1.2 启发式算法

启发式算法具有全局搜索能力强、求解效率高的特点，通常研究人员更多地采用启发式算法。这类算法适用于规模较大的VRP，面对CVRP和VRPTW等约束条件较多的VRP问题时，此类算法仍能较快地获得最终解，缺点是问题规模增大时收敛速度慢，无法得到最优解。常用的启发式算法包括：遗传算法（GA）、模拟退火（SA）、蚁群算法（ACA）、粒子群算法（PSO）、禁忌搜索（TS）、变邻域搜索（VNS）、迭代局部搜索（ILS）、大邻域搜索（LNS）和贪婪随机自适应搜索程序（GRASP）。ZHAO[4]针对随机环境中访问节点对应给定的访问概率，以及访问节点同时有访问概率又带软时间窗的路径规划问题，使用了邻域搜索算法VNS进行求解，其运算速度明显提升。蒋波针对带惩罚函数的VRPTW模型设计了遗传算法，满足配送总成本最小的目标函数[6]。赵辰基于遗传算法求解了从生产中心到仓库之间的路径优化问题，实现了配送路径优化的目的[7]。Mirabi等提出了一种基于模拟退火思想的三步启发式算法求解最小配送时间的多配送中心VRP问题。马炫等提出了一种基于粒子变换原理的整数粒子更新方法求解带时间窗口的车辆路径问题[8]。Angel等基于非确定性的模拟框架，提出了基于贪婪原则的初始解搜索方法，从最近若干节点中选择某一节点，生成多条可行路径，之后结合单一路径中充电节点位置优化、2-Opt和路径间客户点交换三种邻域搜索算法求解[9]。Jun等利用2阶段禁忌搜索算法求解VRPTW问题[10]。Schneider等为了避免单一算法的局限性，利用VNS和TS算法相结合的方法进行求解，在算法早期允许劣解加入候选路径，加快了算法的收敛速度。

1.3 人工智能算法

传统求解方法通常针对具体的问题进行建模求解，并不具备自主学习和决策的能力。随着机器学习技术的推进，目前也出现了通过深度学习等人工智能方法解决上述路径问题的研究成果。徐郁等针对电力物资配送路径问题，建立了以电力物资配送路径长度最小、成本最低、物资需求点满意度最高为目标的多目标优化模型，设计了一种基于深度强化学习（Deep Reinforcement Learning，DRL）的电力物资配送路径优化算法。黄琰等提出了一种基于上置信区间算法改进动作选择的深度Q网络（Deep Q-learning Networks，DQN）方法，相比傳统的DQN方法计算效率得到了提升。王万良等针对多配送中心车辆路径问题（Multi-Depot Vehicle Routing Problem，MDVRP）提出了一种基于多智能体深度强化学习的求解模型，实现了快速获得高质量解的目的。后来Wang等人提出了一种新的DQN模型：Dueling DQN（DDQN），不同于DQN算法，而是把卷积层得到的特征分为状态值和动作优势函数两部分。根据前述相关研究成果的分析，获得VRP的相关算法技术分支表如表1所示：

2 专利分析

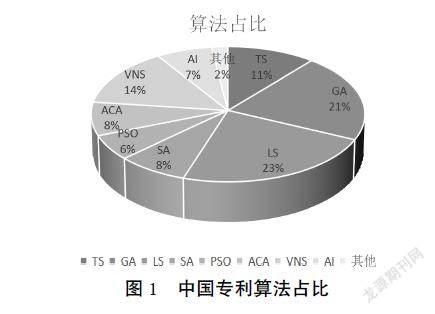
首先针对VRP的中国专利申请进行统计分析，在智能检索系统的CNBAS库中，输入“车辆路径问题”“Vehicle Routing Problem”进行检索，获得116篇中国专利申请，基于各个算法的具体数量，统计出饼状图见图1，可以直观地看出占比较大的是局部搜索算法、遗传算法以及变邻域搜索算法，其他启发式算法占比都比较小；中国VRP相关专利申请中启发式算法占据很大的比重。

且经过检索统计，中国专利申请人的类别中，大专院校和科研单位的占比达73%左右，企业占比为26%，其余为个人申请，可见该技术主题的专利研究主体主要集中在高校和研究院所，也说明该技术问题处在理论研究阶段，商业转化率比较低。

接下来，针对全球VRP领域的专利申请情况进行统计分析，利用Incopat专利检索系统，在Incopat的高级检索框中输入“车辆路径问题”“Vehicle Routing Problem”，为了避免重复，选择相同申请号合并，获得166件全球专利申请，其中涉及精确算法的专利数量为15条，启发式算法的专利数量为166条。全球专利申请的相关算法中，排名靠前的是迭代局部搜索、蚁群算法、粒子群算法、遗传算法和变领域搜索，与中国专利申请统计结果一致，足以说明上述几种启发式算法在求解车辆路径问题中的相对有效性。

由图2可以看出，虽然VRP问題提出是在1959年，但是相关的专利申请是从20世纪90年代才开始。由图2曲线可以看出，相应领域的专利申请量先经过缓慢波动增长，在2012年之后呈快速增加的趋势，并在2018年左右专利年申请量达到了高点。

由于VRP问题属于NP问题，问题复杂度较高，而精确算法仅适合规模较小的情况，启发式算法和人工智能算法由于具有较高的计算效率，所以备受研究人员青睐，为了适应日益复杂的应用场景，追求效率提高和成本降低依旧是该研究领域首当其冲要改进的方面。计算机较强的并行计算能力、多种启发式算法相结合、深度学习等人工智能算法以及大数据等的运用，会为该技术问题的研究提供新的发展空间。

3 相关重点专利

在启发式算法结合方面，广东工业大学在2015年（公开号为CN104951850A）针对多配送中心物流运输车辆路径问题，提出了通过粒子群算法对蚁群算法启发因子进行优化，求解最优配送路径的方法，具有较好的全局和局部寻优能力。同年，还提出了一种求解带软时间窗口物流运输车辆路径问题的方法（公开号为CN104992242A），采用时间窗惩罚机制，建立数学模型，使用自适应混沌蚁群算法求解该模型，具有更好的优化搜索能力，能够避免搜索过程陷入局部最优，提高解的多样性。

在新兴技术应用方面，深圳市德邦物流有限公司于2021年提出了一本基于大数据的智慧物流取件分析系统及方法的专利申请（公开号分别为CN113592440A），该申请已于2022年7月获得专利权，该专利中通过改进型算法的物流配送优化模型，为配送管理员提供科学的路线决策依据，解决了实际出单过程中的问题，保证满足客户需求，提高系统的实用性。

4 结论

随着实际生活中客户需求的多样化，车辆路径问题涌现出了多个变种，多重约束条件的叠加使得问题更加复杂，求解难度也增大，需要不断提出新的模型来满足实际应用场景。同时，随着信息技术与互联网技术的发展，特别是电子商务的快速发展，如何整合社会资源，合理调度多个配送企业的车辆资源从而建立一个车辆调度联盟，也将是车辆路径问题的一个研究方向。因此，未来如果能够针对实际应用场景提出更快速有效的算法，在满足客户需求的基础上降低成本，以灵活应用于多种场景下的路径规划问题，将会在交通运输、货物配送以及物流管理等多个领域产生深刻的影响。

参考文献

[1]Dantzig G， Ramser J. The Truck Dispatching Problem[J]. Management Science， 1959（6）： 80-91.

[2]毕国通. 车辆路径问题及其优化算法研究综述[J]. 物流科技， 2016（6）： 95-97.

[3]Pecin D， Contardo C， Desaulniers G， et al. New Enhancements for the Exact Solution of the Vehicle Routing Problem with Time Windows[J]. Informs Journal on Computing， 2017（3）： 489-502.

[4]ZHAO W H. Study of Routing Problems in Wireless Sensor Networks and Logistics[C]. Doctor Thesis， 2012.

[5]胡剑鹏， 罗霞， 甘易玄. 基于列生成算法的鲁棒电动车路径问题[J/OL]. 计算机集成制造系统： 1-21[2023-04-20]. http： //kns. cnki. net/kcms/detail/11. 5946. TP. 20220520. 1805. 010. html

[6]蒋波. 基于遗传算法的带时间窗车辆路径优化问题研究[D]. 北京：北京交通大学， 2010.

[7]赵辰. 基于遗传算法的车辆路径优化问题研究[D]. 天津：天津大学， 2012.

[8]马炫， 彭芃， 刘庆. 求解带时间窗车辆路径问题的改进粒子群算法[J]. 计算机工程与应用， 2009（27）： 200-202+218.

[9]Angel F M et al. A Heuristic Approach for the Green Vehicle Routing Problem with Multiple Technologies and Partial Recharges[J]. Transportation Research Part E： Logistic and Transportation Review. 2014， 71： 111-128.

[10]Jun Jiang， et al. Vehicle Routing Problem with a Heterogeneous Fleet and Time Windows[J]. Expert Systems with Applications， 2014（8）： 3748-3760.

[11]Yang Xin-She. A New Metaheuristic Bat-inspired Algorithm， Nature-Inspired Coopreative Strategies for Optimization[EB/OL].  Research Gate， 2010.

[12]郎茂祥. 装卸混合车辆路径问题的模拟退火算法研究[J]. 系统工程学报， 2005（5）： 41-47.

[13]辛颖. 基于蚁群算法的车辆路径规划问题求解研究[D]. 长春：吉林大学， 2015.