基于宏观交通的均衡决策控制

摘要 随着智慧城市的快速发展和碳排放进程的推进，车路协同是智慧城市发展的必然结果。智慧车辆不仅自身能根据周围物理环境作出相应的反应，同时还能获取智慧道路各节点或路段的运行状态。为了更好地控制城市交通运行状态和碳中和，文章基于路网宏观基本图（Macroscopic Fundamental Diagram，简称MFD）特性，在车辆协同路网平均旅程车辆完成流率最大基础上，综合碳中和排放、车路协同指标、路网车辆完成率以及子区行程时间，提出了一种宏观交通的均衡决策控制方法。

关键词 车路协同；碳排放；均衡控制；宏观交通

中图分类号 U491文献标识码 B文章编号 2096-8949（2023）09-0020-03

0 引言

我国城市化进程的快速发展，现阶段车路协同以信息集约化、管控协同化的理念整合道路设施，将道路本身及其附属设施通过传感器进行信息采集与数据终端的交互。目前主要利用5G互联网技术与宏观路网中运行的车辆联通，利用采集的大数据、人工智能等技术搭建一个集监测、预警和管控等功能于一体化的系统[1]。

车路协同指标是用来衡量汽车与道路设施之间信息交互效率和准确性的一个指标体系[2]，它包括了交通信号控制、车辆通信等方面的技术指标，旨在提高车辆和道路设施之间的互动效率和安全性。碳中和控制指标是用来衡量企业或国家在减少碳排放方面的成效的一个指标体系[3]。在交通控制过程中，宏观交通控制和碳中和控制两者之间有着协同作用，相辅相成，共同发挥着降低交通对环境影响的作用。

传统交通管控方式，大多从微观的角度进行研究，对复杂的路网OD数据要求较高，对于缓解和改善整个路网交通状态的效果不理想。而利用路网宏观基本特性，可直接进行边界控制更加直接、高效。同时车路协同基础设施的逐步完善，车辆可获取更多的路网实时信息。

利用车路协同基础设施的逐步完善，车辆可获取更多的路网实时信息，结合宏观交通基本控制指标，将同时考虑车路协同指标和碳中和指标。为了将传统的宏观交通控制指标与车路协同指标及碳中和指标同时进行均衡控制决策，该文采用多目标最优的控制方法提高路网运行状态的决策效果。

1 参数设定及建模

1.1 基本假设及约束条件

（1）假设路网车辆在宏观路网中，智慧车辆与智慧道路获取的信息是对称的；碳中和排放量包含新能源车和普通车在宏观路网中运行。

（2）假设各子路车流密度相对均匀，路网累计交通量与路网车辆完成率存在MFD曲线关系[4]。

（3）假设车路协同的宏观路网被划分为R个子区，每个子区均存在车路协同信息交互，各路网子区流入流出i子区的交通流量相对稳定。

1.2 建立模型

基于以上假设车路协同过程中ii子区的累积车辆数分别如下：i子区流入流出的车辆数和运行消失的车辆数。i子区累积车辆数Ni（k）为

i子区内部转移的累积车辆数和i子区转移到j子区的累积车辆数动态平衡方程分别如下[5]：

式中，Nii（k）——子区i累计完成车辆数；Nij（k）——子区i到子区j的累计完成车辆数；Qii（k）——k时间子区i内部交通需求量；Qij（k）——k时间子区i到子区j的交通需求量；Mii（k）——子区i内部累计车辆完成率；Mij（k）——子区i到子区j内部累计车辆完成率。

根据Nikolas Geroliminis[6]研究發现MFD基本图形与交通需求有密切关系，其关系表示为G（n（k））=a[n（k）]3+b[n（k）]2+c[n（k）]，则网子区交通量和车辆完成率之间的关系满足：

式中，pii，gc——造成i子区内部交通需求变化的概率；pij，gc——造成i子区到j子区交通需求变化的概率。

为平衡路网交通流量稳定性和累计交通量之间的关系，对路网MFD子区的车流完成率和增长率提出网络交通流稳定性的指标，以期确定MFD子区控制时机。控制目标函数如下式：

整个路网车辆最大完成率和车辆最小总行程时间约束：

在整个宏观路网车辆运行过程中，车辆的总行程时间与车路协同程度存在一定的联系，其中μi为车辆协同率。车路协同指数最大：

而在宏观路网节点，运行车辆的碳排放较大，因此路网子区碳排放总量最小约束及碳中和排放数值：

式中，——i子区的最高碳中和排放数值；——i子区的最低碳中和排放数值；cni——在i子区实际碳中和排放数值

2 目标函数建立

2.1 多属性效用函数定义

均衡决策方法采用多属性效用决策的分析方法，假设路网车辆最大完成率（Ψ）、区域最小行程时间（H）、碳中和（CN）、车路协同指数（S）为多属性函数，其表达式如下：

λ∶（Ψ， H， CN， S ）λ（Ψ， H， CN， S ）∈ηR （11）

λ=λ（Ψ， H， CN， S ）对偏好关系满足如下条件：

λ（Ψ'， H'， CN'， S' ）λ（Ψ''， H''， CN''， S'' ） （12）

则称函数λ=λ（Ψ， H， CN， S ）为多属性效用函数。

以路网车辆最大完成率（Ψ）、区域最小行程时间（H）、碳中和（CN）、车路协同指数（S）为变量的函数λ=λ（Ψ， H， CN， S ），可以在智慧城市宏观路网中，通过对以上四个决策指标进行均衡及控制，能够有效地提高车辆的运行效率、减少碳排放等多方面的效益。对于四者共同产生的综合效益，应越高越有利于宏观交通控制的发展和车路协同先进技术的改进。

项目全过程咨询过程中Ψ、H、CN、S均衡优化目标函数为多属性效用函数λ=λ（Ψ， H， CN， S ），其目标值为λ=λ（Ψ， H， CN， S ）的最小值。

2.2 目标函数建立

根据多属性效用函数加性定理[7]，λ=λ（Ψ， H， CN， S ）能够分解成以下形式：

λ（Ψ， H， CN， S ）＝μΨλ（Ψ）+μHλ（H）+μCNλ（CN）+μSλ（S）（13）

μΨ+μH+μCN+μS=1 （14）

式中，λ（Ψ）、λ（H）、λ（CN）、λ（S）分别为路网车辆最大完成率（Ψ）、区域最小行程时间（H）、碳中和（CN）、车路协同指数（S）的单一变量的效用函数。效用函数的存在性及不唯一性，因遇到的交通拥堵采取防范措施的态度，故该文单一变量的效用函数为凹函数，将其建设为二次函数，则为U（x）=a（x?x0）2+b，其中a<0。μΨ、μH、μCN、μS分别为各效用函数的各自对应的权重，可以通过交通仿真确定，其表现为驾驶人对不同路径的偏好。

2.3 约束条件

约束条件是求解多目标问题的重要组成部分，路网车辆最大完成率（Ψ）、区域最小行程时间（H）、碳中和（CN）、车路协同指数（S）之间相互约束关系和各自的目标共同约束。

以上述的假设为基础，在假设建设单位知道项目全过程咨询过程中的信息条件下，均衡优化模型的约束条件如下：

（1）碳中和排放约束。能够得出子区i实际车辆行程时间—碳中和排放（T—CN）之间线性关系的斜率如下：

则子区i的实际碳中和排放量如下：

子区i的实际碳中和排放均处于路网子区的最小碳中和排放和最大碳中和排放之间，即。

（2）车路协同指数约束。能够得出路网子区i与车辆行程时间之间线性关系的斜率如下：

3 仿真分析

根据路网密度数据，该路网交通分布不均匀存在一定的差异，按照路网结构属性划分为若干个理想MFD子区。

车路协同路网仿真时间为5 h。仿真初始时刻，各路网子区的车辆数n为0，各子区交通需求车辆数为800 pcu。仿真0～2 h，交通需求量线型增加，其中增加量为1 100 pcu/h。2～5 h，交通需求量线性减少，其中减少量为1 000 pcu/h。若i子区与j子区之间双向均采用边界控制，由于子区之间流向相反且配时不同，实际实施中可采用非对称相位进行控制。

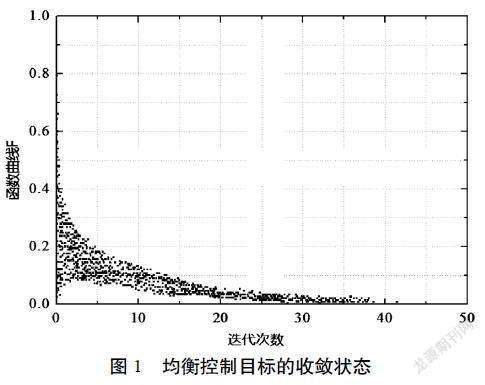
静态均衡因子是指在一个特定时间点内，各个因素之间的平衡关系。在制定决策和控制执行过程中，如果只考虑静态均衡因子，通常只需要考虑当前状态下的各个因素之间的平衡关系。动态均衡因子是指在一段时间内，各个因素之间的平衡关系。在制定决策和控制执行过程中，如果要考虑到未来变化的趋势，就需要考虑动态均衡因子。均衡决策控制的4个优化目标的函数矩阵约经过50次迭代达到收敛，如图1所示。

图1 均衡控制目标的收敛状态

该文采用的10个状态的区间划分方式在一定程度上压缩了收敛时间，同时保证了算法的精度。均衡因子的多目标控制模型算法具有计算时间短和动态控制性的优势，符合该文决策的实时性要求。

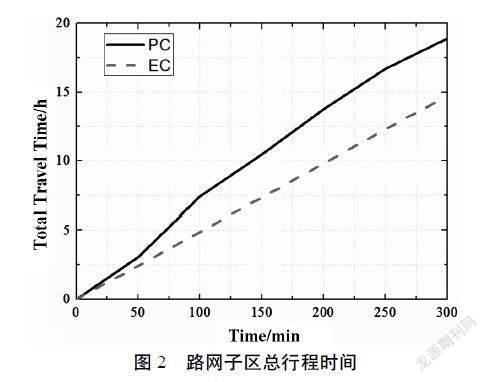
基于动态均衡因子的多目标控制模型算法在不同控制方式下的决策效果与一般单一目标决策结果进行对比。根据图2对比显示，对于整个车路协同路网而言，路网每辆车平均每公里行程时间之和等于总行程时间之和，在均衡控制法下比控制法降低了4.37%，对于路网平均延误而言，均衡控制（EC）下比交通管控（PC）下的延误值降低了5.67%。均衡控制方法能够有效地提高路网旅行车辆完成流率和旅行车辆完成交通量。

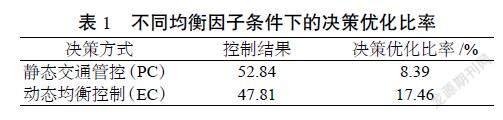
通过对比不同均衡因子的均衡决策方式，最终优化比率分析得到表1数据。

对比分析表1显示，传统交通控制决策和动态均衡控制优化比率分别降低为8.39%和17.46%，因此动态均衡控制优于传统交通控制方法。

4 结论

该文从车路协同的宏观路网角度进行研究，在路网车辆最大完成率（Ψ）、区域最小行程时间（H）、碳中和（CN）、车路协同指数（S）为车路协同的宏观路网的控制指标，从智慧城市的宏观路网角度进行均衡控制，通过相关参数的变化情况，仿真结果表明：

（1）在满足路网旅行车辆完成率高和车辆总行程时间小，实现智慧道路的协同，有效缓解交通运行状态。

（2）通过确定车路协同路网的协同指数收益进行均衡控制，通过具体交通分配方法，可有效减少交通拥堵及拥堵扩散。

（3）该文提出的均衡控制决策方法，在实际中，可考虑利用均衡控制策略有效降低智慧城市宏观路网车辆总行程时间和平均延误时间，减少出行成本。

（4）通过确定车路协同指标，减少在路网节点的车辆碳排放，缓解出行对控制的污染。

参考文獻

[1]GONZALES E J， CHAVIS C， LI Y， et al. Multimodal Transport Modeling for Nairobi， Kenya： Insights and Recommendations with an Evidence Based Model[R]. UC Berkeley Center for Future Urban Transport， 2009.

[2]陈超， 吕植勇， 付姗姗， 等. 国内外车路协同系统发展现状综述[J]. 交通信息与安全， 2011（1）： 102-105+109.

[3]庄贵阳， 窦晓铭. 新发展格局下碳排放达峰的政策内涵与实现路径[J]. 新疆师范大学学报： 哲学社会科学版， 2021（6）： 124-133.

[4]CASSIDY M J， JANG K， DAGANZO C F. Macroscopic Fundamental Diagrams for Freeway Networks： Theory and Observation[J]. Transportation Research Record Journal of the Transportation Research Board， 2012（1）： 8-15.

[5]丁恒， 朱良元， 蒋程镔， 等. MFD子区交通状态转移风险决策边界控制模型[J]. 交通运输系统工程与信息， 2017（5）： 104-111.

[6]GONZALES E J， CHAVIS C， LI Y，  et al. Multimodal Transport Modeling for Nairobi， Kenya： Insights and Recommendations with an Evidence Based Model[R]. UC Berkeley Center for Future Urban Transport， 2009.

[7]章志敏. 多属性效用函数及其应用[J]. 运筹学杂志， 1993（2）： 61-63.