菱形的“寻根之旅”

文／范志群

中考以菱形为背景的题目层出不穷，这类题往往题型复杂，有一定的难度。但是，当我们逐层剖析，追根溯源时，会发现这些题目其实就是考查菱形的基本性质和判定方法，归根到底，还是我们教材中的基本知识和基本方法的具体应用。下面，让我们一起踏上菱形的“寻根之旅”。

【中考链接】如图1，将矩形纸片ABCD（AD＞AB）折叠，使点C 刚好落在线段AD上的G 点，且折痕分别与边BC、AD 相交。设折叠后点C、D 的对应点分别为点G、H，折痕分别与边BC、AD相交于点E、F。

图1

（1）判断四边形CEGF的形状，并证明你的结论；

（2）若AB=3，BC=9，求线段CE 的取值范围。

【解析】（1）利用轴对称的性质、三角形全等，可证得四边形CEGF是菱形；

（2）求CE 的取值范围，我们可以转化为求CE的最大值和最小值。

如图2，当点F 与点D 重合时，四边形CEGF 是正方形，此时CE 最小，且CE=CD=3。

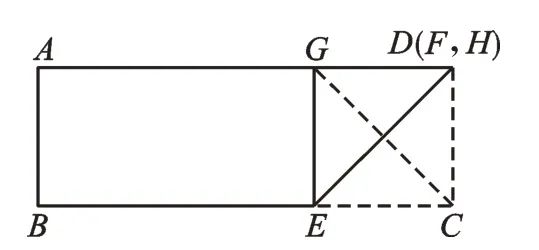
图2

如 图3，当 点G 与 点A 重 合 时，CE最大。

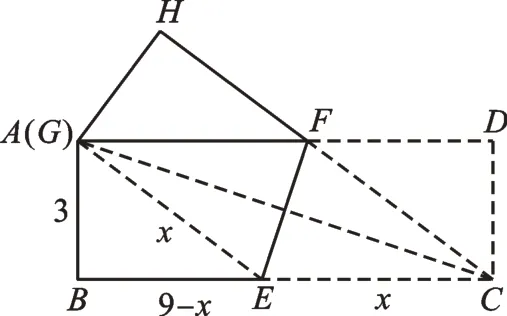
图3

设CE=x，则BE=9-x。

由（1）知AE=CE=x，

由勾股定理得AB2+BE2=AE2，即

32+（9-x）2=x2，得x=5。

所以线段CE的取值范围为3≤x≤5。

本题第（1）问对同学们来说应该是“熟脸”；对于第（2）问，有的同学被迷惑住了，不知如何入手。第（2）问看似是个新题，实际上却出自我们的教材。下面，我们一起来探寻它的“根”在哪里。

我们一起回顾一下苏科版八（下）数学教材93 页第15 题：由两个等宽的矩形叠合而得到的四边形ABCD 是菱形吗？证明你的结论。（图略）

该问题不正是中考题第（1）问的原型吗？如果紧接着追问：此时的菱形边长什么情况下最大？什么情况下最短？这个追问不就是这道中考题的第（2）问——求菱形边长的取值范围吗？

【归纳】解决翻折中的问题时，我们常常会找相等的线段，利用勾股定理，设未知数，构建方程。教材是我们学习知识的“根源”，每年都有大量的中考题来源于教材。我们要学会细心观察，精心分析，才能“追根溯源”，使问题迎刃而解。