集中式MIMO雷达研究进展：正交波形设计与信号处理

黄 磊，柳艾飞，高才才

（1.深圳大学电子与信息工程学院，广东深圳 518000；2.西北工业大学软件学院，陕西西安 710129；3.深圳市华讯方舟微电子科技有限公司，广东深圳 518100）

0 引 言

多输入多输出（Multiple Input Multiple Output,MIMO）源自增加通信信道容量而研发的多天线技术［1-3］。无线通信中的MIMO 发射天线通常是分布式布放，天线间距足够大，以确保多个发射天线和接收天线之间的无线信道相互独立；从而可以通过空间分集，减轻多径衰落对信号传输的影响。

新世纪以来，复杂多变的战场环境给雷达系统抗截获性能、目标检测性能等提出更高要求，受MIMO 技术在通信领域成功应用的启发，MIMO 技术被拓展到雷达系统。MIMO 雷达按照天线的排布方式，可以分为分布式MIMO 雷达和集中式MIMO雷达。

分布式MIMO 雷达天线的布放方式与分布式MIMO 通信天线类似，其收发天线的阵元间距很大，各阵元可以从不同视角观察目标，克服目标雷达截面积（Radar Cross Section,RCS）的闪烁效应,获得空间分集增益，提高雷达对目标的探测性能［4-8］。

集中式MIMO 雷达与分布式MIMO 雷达不同，其收发天线各阵元间距与感兴趣目标信号的波长可比拟［9-22］。集中式MIMO 雷达发射信号波形主要有部分相关信号和正交信号。部分相关信号通过设计发射波形相关矩阵，将辐射能量集中于空间感兴趣的区域，或者匹配于一个给定的方向图，从而获得部分相关积累增益，提高雷达系统对感兴趣目标的探测性能［15-18］。当MIMO 雷达发射波形为正交信号时（称为正交波形MIMO雷达），发射波形在空间不能相参合成高增益窄波束，而是形成M个独立的低增益宽波束，导致回波信号的信噪比损失，减小了雷达的作用距离。但发射正交波形的优点是在每个接收天线处，可利用波形正交性进行匹配滤波，将对应于M个发射波形的目标回波进行分离，获得M路回波信号。因此，在接收端可获得MN个虚拟阵元（即N个阵元的接收天线孔径拓展了M倍），从而显著提升杂波/干扰的抑制能力、提高参数的估计精度等［9-14］。然而，正交波形MIMO 雷达这些性能提升的前提条件是发射波形具有正交特性。事实上，在实际应用中，在不牺牲时域/频域资源情况下，时宽带宽积受限的雷达波形无法提供理想的正交特性［19］。此时，发射波形之间的相关性总是存在。这意味着，在接收天线端发射波形之间的互相关会影响目标探测性能，尤其是在多目标和/或杂波场景下，即便很弱的相关性也会造成探测性能的明显下降［20］。为了降低正交波形MIMO 雷达的发射波形互相关对接收端探测性能的影响，可以改进发射波形设计方法，从源头上降低发射波形互相关。另一条思路是在接收端对滤波器进行失配设计；失配滤波是单输入单输出雷达降低自相关旁瓣的经典方法［21-23］，近年来被拓展到MIMO雷达中，用来降低接收滤波器输出中的互相关成分并保证低的自相关旁瓣和信干噪比损失在可接受范围之内［24-25］。

本文主要对正交波形MIMO 雷达的波形设计与基于匹配滤波的信号处理进行归纳综述。集中式MIMO 雷达发射波形的正交性可在脉内编码实现（称作快时间编码），也可以在脉间编码实现（称作慢时间编码）。脉内编码实现的正交波形主要包括三种快时间复用方式：时分复用、频分复用、码分复用。对MIMO雷达正交波形的设计，其代价函数通常是自相关峰值旁瓣能量，或自/互相关积分旁瓣能量。最小化代价函数的常用算法包括遗传算法、模拟退火算法、二次规划算法和贪婪算法等。MIMO 雷达正交波形的慢时间编码，通过优化发射波形每个脉冲的初始相位获得正交性。经典慢时间编码波形的脉冲初始相位按照线性调制，从而在多普勒域实现发射波形分离。

本文针对集中式MIMO 雷达正交波形的编码技术进行归纳，指出其优缺点。同时，给出MIMO雷达数据模型和信号处理流程。此外，仿真验证了基于不同正交波形的MIMO雷达目标成像效果。最后，本文阐述了当前集中式MIMO雷达面临的技术问题和发展趋势。

1 MIMO雷达发射波形

集中式MIMO 雷达利用发射波形之间的正交性，在接收天线端获得发射波形自由度，从而显著提高角度分辨率和低截获能力。为了获得无角度模糊的高分辨角度估计，MIMO 雷达阵列排列方式通常如图1所示［26］。在图1中，λ为雷达信号波长，N为接收阵元数，M为发射阵元数。譬如，若N=4，M=4，在接收端利用发射波形的正交性，可以获得16 阵元的虚拟阵列，虚拟阵列阵元间隔为λ/2。从图1可见，虚拟阵列的阵元自由度是实际阵元自由度（M+N=8）的2倍。

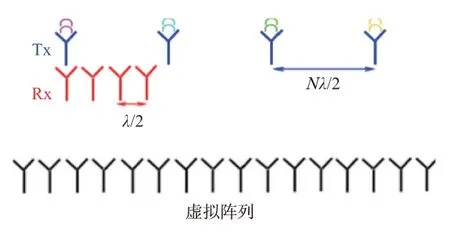
图1 MIMO雷达虚拟孔径示意图

MIMO 雷达发射波形通常可以分为快时间编码波形和慢时间编码波形。快时间编码波形通过脉内调制实现正交性，而慢时间编码波形主要通过脉冲之间的初始相位编码实现正交性。另外，还有对脉内和脉间同时进行编码的波形，此类波形同时使用了快时间和慢时间编码，属于混合编码［27］。

1.1 快时间编码波形

1.1.1 正交性条件

MIMO 雷达正交波形集最初的正交条件为零时延互相关为零，即

式中，sk(t)和sl(t)分别为第k个天线和第l个天线的发射波形，Tp为波形脉冲时间长度。

此正交性条件没有考虑多目标场景下的旁瓣互扰。对于多目标或者杂波场景条件下，还需要考虑不同发射波形之间的非零时延互相关为零，即

式中，τ为时延，ℝ表示实数域。

对于快时间编码波形，在正交性条件式（2）下，可以对多目标进行完全分离。但在式（2）条件下，需要满足

式中，ℱ 表示傅里叶变换运算，Sk(f)和Sl(f)分别为波形sk(t)和sl(t)的傅里叶变换。根据式（3）可知，假设发射波形不使用时域分集，此时若要满足式（2）的正交性条件，需要第k个和第l个发射波形在频域完全无重叠。实际中，为了用集中式MIMO 雷达对同一目标的反射回波进行相干组合，需要发射波形在频谱区域上有较大重叠［20］。对于快时间编码波形，在不牺牲时域或频域条件下，式（2）的正交性条件在实际雷达应用中通常无法满足。因此，对于MIMO 雷达发射波形，需要设计满足零时延互相关正交性条件（式（1）），同时具有非零时延弱互相关性的波形集。另外，需要满足雷达波形设计的基础要求，即低自相关旁瓣条件。

根据上述正交波形设计的要求，MIMO 雷达正交发射波形的快时间编码可划分为：时分复用MIMO（Time Division Multiplexing MIMO,TDMMIMO）、码分复用MIMO（Code Division Multiplexing MIMO,CDM-MIMO）、频分复用MIMO（Frequency Division Multiplexing MIMO,FDM-MIMO）［28-41］。下面针对这些典型MIMO 雷达波形的设计原理展开概述，指出其优缺点。

1.1.2 TDM-MIMO波形

传统TDM-MIMO 波形集合利用时域差异获得正交性。具体来讲，其所有发射波形共享同一带宽，但在不同时隙发射。第k个发射波形可表达为

式中，△t为相邻天线发射脉冲的时间差。

由于TDM-MIMO 实现简单，最早在车载毫米波雷达、室内人员感知雷达中广为应用［40-42］。但是由图2可知，相邻两个波形的时延差△t至少为脉冲宽度Tp与回波的最大时延之和。而每个发射波形的脉冲重复周期Tr至少为M△t。若脉冲重复周期过长，导致脉冲重复频率（Pulse Repetition Frequency,PRF）减少，此时对高速运动目标，会出现多普勒模糊问题；因此TDM-MIMO 波形在对高速运动目标进行探测的军用雷达中很少应用；在无人驾驶等民用领域，需要补偿此多普勒模糊才能实现对多目标正确测向［43-44］。另外，在TDM-MIMO中，由于每个时刻只有一个发射天线发射信号，发射功率受限于单个天线的最大发射功率，导致由于能量积累不够而降低了对弱小目标的发现概率。因此，TDM-MIMO 通常用于短距离慢速目标探测的低功率雷达，比如用于自动驾驶的雷达以及室内人员监测雷达［40-42］。

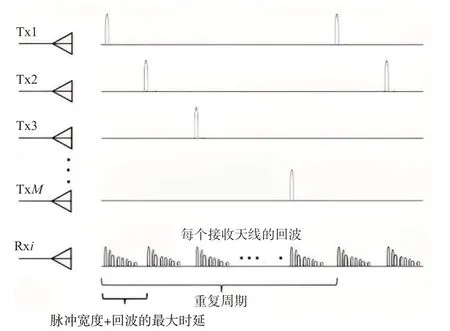
图2 传统TDM-MIMO波形示意图［32］

时间叉排（Time-Staggered）线性调频连续波属于TDM-MIMO 波形［29-31］。与传统的TDM-MIMO 波形集不同，时间叉排线性调频连续波利用时间上交叉排布的线性调频信号实现发射波形正交性，如图3所示。时间叉排MIMO 正交波形在超视距雷达中得到成功应用［29］。但其只适用于连续波雷达，不能用于常规的脉冲多普勒雷达中。另外，其降低了多普勒无模糊范围。

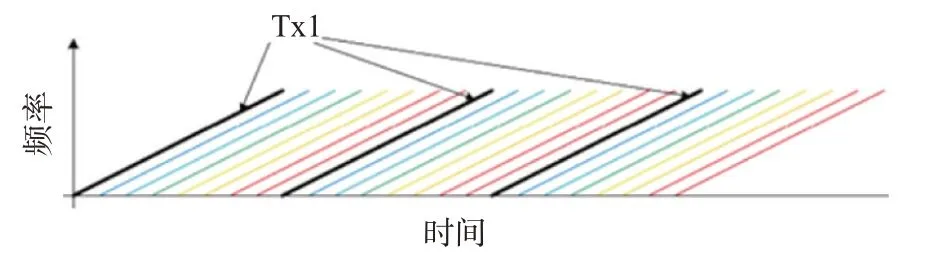
图3 基于时间叉排的TDM-MIMO波形示意图［26］

表1给出MIMO 雷达使用不同发射波形时，其优缺点比较。注意，在探测距离范围内，满足式（2）的波形为严格正交；仅满足式（1），不满足式（2）的波形为近似正交。若接收端信号处理结果的距离旁瓣/多普勒旁瓣/距离分辨率与SIMO 雷达处理结果类似，我们称之为低距离旁瓣/低多普勒旁瓣/高距离分辨率；另外，表1中的多普勒模糊，也是以SIMO 雷达为基准作比较得到的。

表1 传统TDM波形与时间叉排TDM优缺点比较

1.1.3 CDM-MIMO波形

虽然TDM-MIMO 实现简单，但因其在每个时隙只有一个发射天线工作，故TDM-MIMO 不能完全利用MIMO 天线发射端性能。与TDM-MIMO 不同，CDM-MIMO 把每个发射脉冲划分为多个码片（也称作子脉冲），每个码片使用不同的初始相位，从而使得多个发射波形之间获得正交性。第k个发射波形表达式为

式中，Tp为脉冲宽度，sck(t)为第k个发射波形的码片波形，Lc为码片个数，Tc为码片时间宽度，ϕk,lc为第k个发射波形的第lc个码片的初始相位。

CDM-MIMO 波形的编码相位可以为0、π 二值相位，也可以为多值相位；二值相位调制实现简单，但理论证明发现多值CDM 波形可以获得更低的互相关［45］。基于二值相位的CDM-MIMO 示意图如图4所示。这里，Code 1 与Code 2 分别对应于相位调制项{}和{}。在CDM-MIMO中，M个发射天线可同时发射信号，因此与TDM-MIMO 相比，其发射功率增加了M倍。这相当于获得10log10(M)dB的信噪比增益。

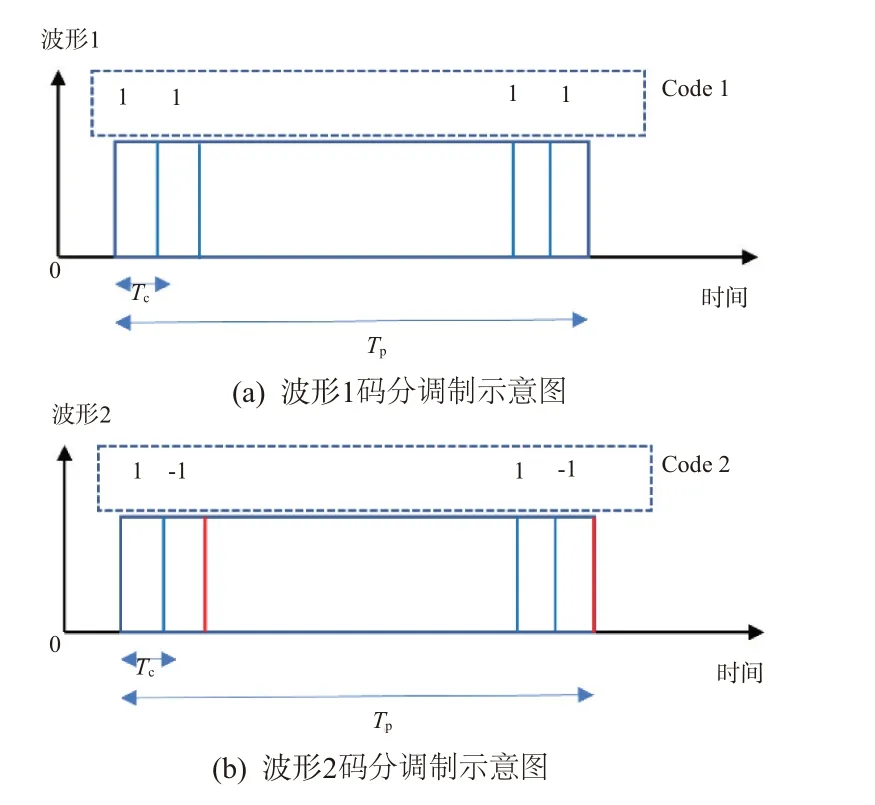
图4 CDM-MIMO波形示意图

典型的二值CDM-MIMO 波形有Gold、APAS（Almost Perfect Autocorrelation Sequences）、ZCZ（Zero Correlation Zone）等编码波形［46］。典型的多相位编码CDM-MIMO 波形有基于遗传算法和传统迭代码选择寻优方法的编码波形［35］。还有基于互相关代价函数，在0 到2π 之间寻优搜索相位值的多值Cyclic Algorithms-New（CAN）编码波形［34］。这些CDM-MIMO 波形集均能获得式（1）所示的零时延迟零多普勒条件下的正交性。根据Welch 下界限，2 个相位编码序列之间的互相关受限于码长［45］；为了降低互相关，需要较长的码长，这导致接收端信号处理计算复杂度增加。另外，CDM-MIMO 波形对于高速运动目标的多普勒容忍性通常较差［47-48］。表2给出MIMO 雷达使用不同CDM 发射波形时，其优缺点比较。

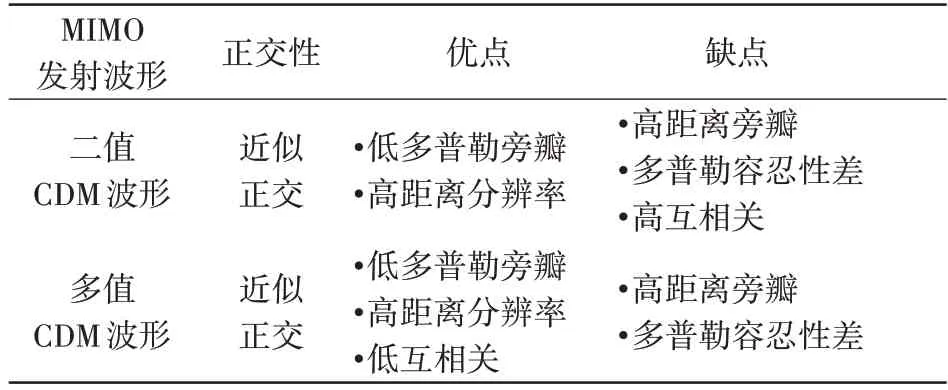
表2 不同CDM波形优缺点比较

1.1.4 FDM-MIMO波形

OFDM-MIMO（Orthogonal FDM-MIMO）波形是典型的频分复用正交波形。

图5所示为一种基于交叉技术的OFDM-MIMO 载波分配方式［49］，其中，Tx1 和Tx2 分别为发射天线1 和2，交叉技术使得所有天线在同一时刻发射相互正交的信号。同时，为了避免距离单元间回波互扰，需要在OFDM 信号前加入循环前缀（Cyclic Prefix,CP），构成CP-OFDM-MIMO 波形，这造成发射功率损失［50］。而且如图5所示，每个发射波形的OFDM 信号使用多个子载波时，OFDM 信号为非横模信号，雷达不能实现最大功率发射。另外，由于OFDM 发射波形正交性依赖于单频正弦波之间的不相关特性，其对于动目标Doppler 容忍性较差。因此，需要研究恒模OFDM-MIMO 波形并提高其多普勒容忍性［50-51］。尽管OFDM-MIMO 波形在雷达中应用时存在发射功率损失以及多普勒容忍性很差等问题，但如图6所示，由于CP-OFDM-MIMO 波形的零距离旁瓣优点，仍为雷达弱目标探测提供了可能性［52］。另外，由于OFDM 技术在通信中的成熟应用以及频谱资源紧张与雷达感知需求提升之间的矛盾，促使OFDM-MIMO 成为雷达系统与通信系统频谱共享以及雷达和通信一体化的重要方法［53-54］。

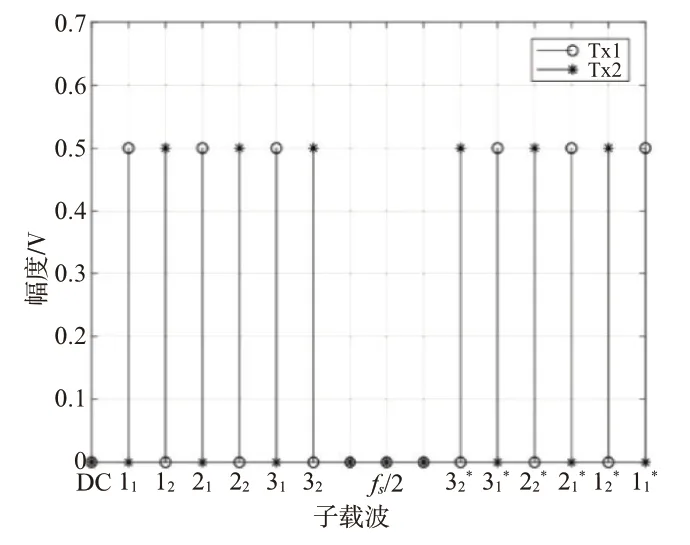
图5 交叉OFDM-MIMO波形示意图［49］

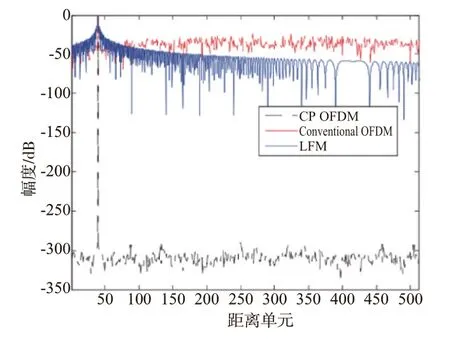
图6 CP-OFDM-MIMO雷达点目标一维距离像以及传统LFM雷达和OFDM雷达点目标一维距离像［52］

另一种典型的FDM-MIMO 波形为线性调频（Linear Frequency Modulation,LFM）频分波形，如图7所示。图中第l个发射波形的表达式为

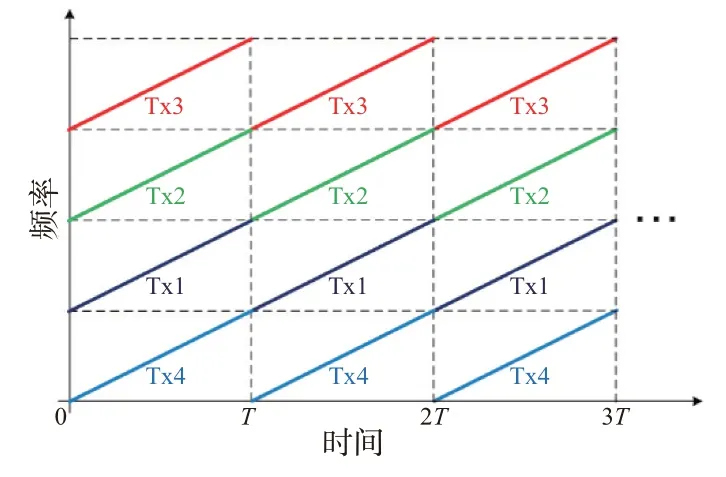
图7 FDM-LFM MIMO波形示意图［26］

式中，

T为子脉冲时间宽度，K为连续子脉冲个数，fln为第l个发射波形的第n个子脉冲的载波频率，β为调频率。

注意到图7所示的FDM-LFM 波形集合中在同一个子脉冲内，不同发射信号占用不同频段，而目标在不同频段的回波特性可能发生变化。因此，不同发射天线回波之间的相关性可能会降低，从而影响后续基于相干信号处理的目标检测性能以及杂波抑制［1,20,27,55］。另外，在图7所示FDM-LFM MIMO 波形集合中，每个波形占用的带宽是系统带宽的1/4 倍，从而造成距离分辨率下降。另外，由于发射波形的中心频率与阵元之间的线性关系，导致接收端经过距离向压缩和波束形成处理后存在距离-角度耦合。为消除此耦合现象，可以对每个发射波形的中心频率进行随机选取，此时需要发射天线数目足够多（例如含有25 个发射天线的RIAS 系统）［14］。表3给出MIMO 雷达使用不同FDM发射波形时，其优缺点比较。

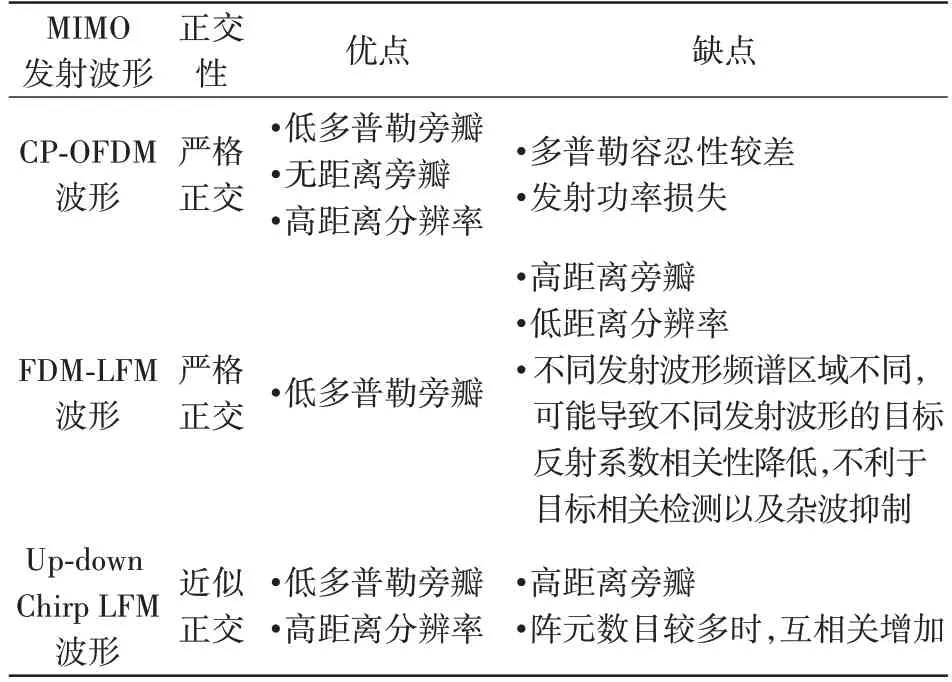
表3 不同FDM波形优缺点比较

与FDM-LFM MIMO 波形不同，基于Up-down Chirp 调制的FDM-MIMO（记作Up-down Chirp FDM-MIMO）在同一个时间段内，不同发射波形使用相同频段，可以避免不同发射波形回波信号相关性降低的问题［36］。Up-down Chirp FDM-MIMO 发射波形集利用发射信号的时频图波形差异实现波形正交，不牺牲频域资源或者时域资源，其示意图如图8所示。在图8中，优化变量为时间分割点tm1。以所有互相关峰值、一定时延内的自相关旁瓣以及互相关进行线性组合建立代价函数。通过最小化代价函数，可获得最优的tm1，m∈{}1,…,M。从图8可见，不同发射波形具有相同的频谱范围，不会破坏后续的相干信号处理。Up-down Chirp FDM-MIMO 发射波形的互相关基本不随时延变化，导致接收端综合积分旁瓣不会像自相关一样随着时延降低。

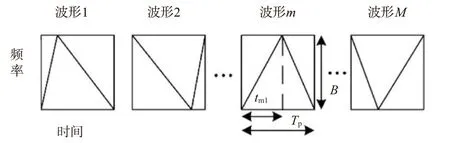
图8 Up-down Chirp FDM-MIMO 波形示意图［36］

1.2 慢时间编码波形

1.2.1 正交性条件

慢时间编码波形的正交性通过对每个脉冲的初始相位进行编码实现。具体来讲，一个相干积累时间（CPI,Coherent Process Interval）内第m个天线的发射波形为

式中，Tr为脉冲重复周期，sp(t)为一个脉冲内的发射波形，其对所有天线均相同，αm(lTr)为第m个发射波形随慢时间l变化的脉冲初相，L为一个CPI内的脉冲个数。那么，慢时间编码波形的正交性条件为

从式（8）可见，慢时间编码波形只是对每个脉冲的初始相位进行编码，而所有发射波形的脉冲内调制方式都相同；从式（9）可见，不同发射波形在一个相干积累时间内对每个脉冲的初相赋予不同的值，实现不同发射波形的脉冲初相序列正交，即慢时间编码。

1.2.2 DDM-MIMO波形

经典的慢时间编码波形为相位线性编码波形，即多普勒码分波形（Doppler Division Multiplexing-MIMO,DDM-MIMO［56］)，也称作多普勒码分多址（Doppler Division Multiplexing Access,DDMA）。具体来讲，DDM-MIMO第m个波形的相位为

式中，fd(m)为第m个发射波形的多普勒频率，表示为

其中，fdMax=1/Tr。

值得注意的是，公式（10）中的时域慢时间线性调制，对应于多普勒域频谱搬移。由于每个发射波形多普勒域间隔为fdMax/M，从而保证多个发射波形可以在多普勒域完全分离，因此DDM-MIMO波形是理想正交的。但DDM-MIMO 存在多普勒模糊，降低了可检测的动目标速度范围［57］。

除线性相位调制外，抖动（Dithered）DDMA 对每个发射波形增加一个随机产生的固定值相位，来抑制DDM-MIMO 的模糊问题；其具体实现为第m个发射波形在第l个脉冲的初相改变为

式中，φm为[0 2π]上随机选取的相位，(m)在M个多普勒{}fd(1),fd(2),…，fd(M) 中随机选取。

抖动DDMA 可以抑制DDMA 的多普勒模糊，但同时带来了信噪比损失和多普勒旁瓣升高问题。

1.2.3 慢时间随机相位编码MIMO波形

Dithered DDMA 波形可以明显抑制DDMA 的模糊问题，但其又引入了高多普勒旁瓣问题。为了克服此问题，文献［58］提出了慢时间随机相位编码波形，其初相为

式中，ϕm(l)为均匀分布于[]0 2π 的随机值。慢时间随机编码波形不存在多普勒模糊，但其多普勒旁瓣仍然较高。

与快时间编码波形相比，慢时间编码波形只是改变每个脉冲的初相，而其脉冲波形相同，并可延续使用经典的LFM 波形。另外，慢时间编码波形的发射端硬件实现简单、成本较低。然而，慢时间DDM-MIMO 存在多普勒模糊问题，从而降低了可检测目标的最大速度。同时，慢时间随机相位编码MIMO波形的多普勒旁瓣较高，不利于运动目标检测。表4给出MIMO 雷达使用不同慢时间发射波形时，其优缺点比较。

表4 不同慢时间编码波形比较

从以上分析可见，总体来说快时间编码是利用脉冲内调制实现正交性，不利用慢时间资源，因此可以获得低多普勒旁瓣。但是由于对距离向快时间资源的利用，除传统TDM 波形以外，其他快时间编码波形通常会导致距离旁瓣升高。而TDM 又面临发射功率损失以及多普勒模糊的问题。在硬件实现方面，TDM 波形继承了SIMO 雷达中的通常使用的脉内调制方式（比如LFM 调制），其实现简单，比如TI 公司的IWR1642 毫米波传感器就采用了TDM-MIMO技术。

另一方面，慢时间编码是利用脉冲的初始相位调制实现正交性，不利用快时间资源，因此可以获得低距离旁瓣。但是由于对慢时间资源的利用，慢时间编码波形通常会导致多普勒旁瓣升高或者多普勒模糊问题。在硬件实现方面，慢时间编码可以继承SIMO 雷达中的通常使用的脉内调制方式，与除传统TDM 外的大多数快时间编码相比，实现通常较为简单。比如TI 公司的IWR1642毫米波传感器中也采用了基于二值相位的慢时间编码波形，而AWR2944 毫米波传感器中采用了DDM 波形；与基于传统TDM 的方式相比，慢时间编码波形提高了发射功率，可增大探测距离［59］。

把快时间域和慢时间域编码结合起来，获得这两个域中编码的优点，可以进一步提高波形复用的性能。文献［27］展示了快时间CDM 和慢时间DDM相结合的发射波形优越性。

2 集中式MIMO雷达统一信号处理框架

针对上述正交/近似正交MIMO 雷达发射波形，本节给出基于匹配滤波的集中式MIMO雷达信号处理框架。对于MIMO 雷达，M个发射波形同时发射，因此经过目标反射后，接收端信号为M个发射信号的线性组合。为了在接收端充分利用发射端自由度，在每个接收阵元后接M个匹配滤波器（Matched Filter,MF），对于慢时间DDM 编码波形，还需对滤波器输出进行Doppler 滤波，最终在接收端获得MN的空域自由度。

注意本节主要把快时间编码和慢时间编码的接收信号处理统一到一个框架内，描述了接收端的匹配滤波处理过程；当然实际系统还包含后续的数字波束形成（Digital Beamforming,DBF）、动目标指示（Moving Target Indication,MTI）、动目标检测（Moving Target Detection,MTD）或者空时自适应信号处理（Space-Time Adaptive Processing,STAP）以及恒虚警处理［60］。另外，匹配滤波器和后续数字波束形成器可以交换顺序，用以节省计算复杂度［61］。

2.1 MIMO雷达信号模型

集中式MIMO 雷达发射、接收信号示意图如图9所示［9-10］。

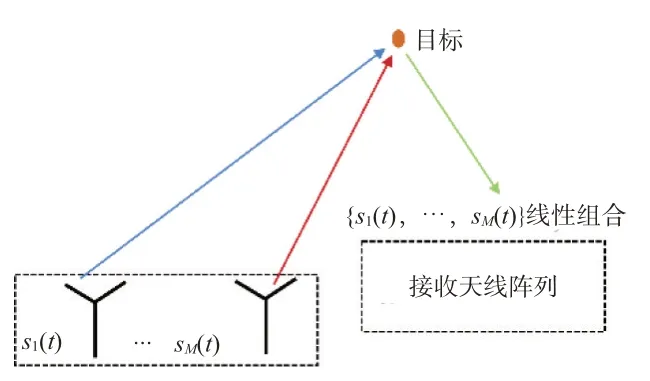
图9 MIMO雷达信号发射接收示意图

设某一点目标在位于MIMO 雷达的远场。那么，雷达天线发射窄带信号，点目标处的反射信号为发射信号的线性求和，具体可以表示为

式中，vt,l=t-lTr-τT(r0),f0为雷达载波频率，τT(r0)为发射波形到达目标的时延，r0为目标相对于雷达的距离；Δm(θ0)为时延导致的发射阵元之间的相位差。以第一个阵元为参考，我们有Δ1(θ0)=0，这里θ0为目标角度，α0为目标反射系数，fd为目标与雷达观测平台之间的相对运动造成的多普勒频率。因此，由式（14）容易得到

定义第n个接收天线的接收信号为yn(t,l)，则

定义接收导向向量为

所以，接收数据向量可以写为

式中，e(t,l)为噪声向量。

2.2 统一信号处理框架

对接收数据向量y(t,l)的信号处理流程如图10所示，其中MFml为对第m个发射波形在第l个脉冲的匹配滤波器（Matched Filter）。对于快时间编码波形，M个匹配滤波器滤波器对应于M个不同的发射波形，MFml只随m变化，与l无关。对于慢时间编码波形，M个匹配滤波器对应于同一个发射波形，其初始相位随脉冲变化，即MFml只随着脉冲l变化，与m无关。快时间编码波形和慢时间编码波形的匹配滤波分别由式（20）和（21）给出。

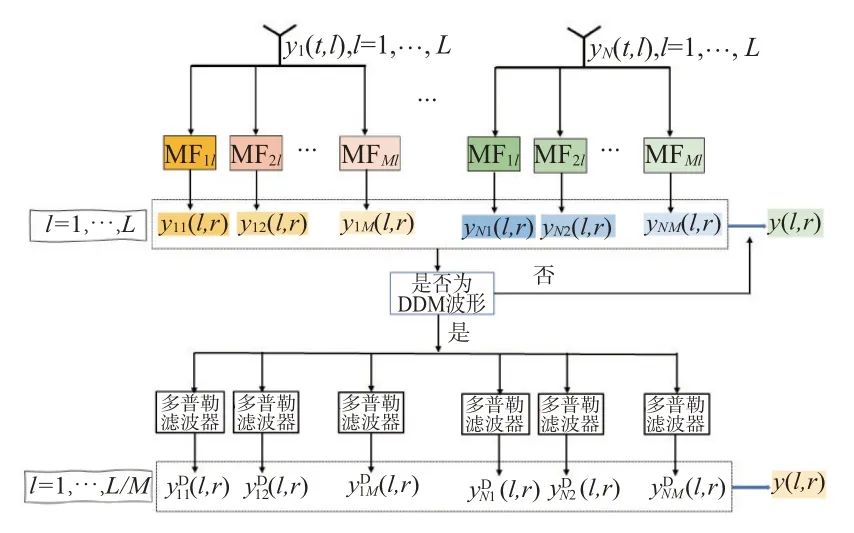
图10 MIMO雷达信号处理

对于快时间编码MIMO，第n个接收天线数据通过第m个匹配滤波器后，其输出为

对于慢时间编码MIMO，第n个接收天线数据通过第m个匹配滤波器，其输出为

对于慢时间编码DDM-MIMO 波形，匹配滤波器输出需要经过Doppler 滤波器后才能实现接收端发射波形分离。Doppler 滤波器输出定义为(l,r)。

对于快时间编码MIMO 和慢时间编码MIMO（DDM-MIMO除外），定义匹配滤波后的向量为

对于慢时间编码DDM-MIMO，定义经正交波形匹配滤波和Doppler滤波后的数据向量为

经过化简，可以得到

式中，cauto(r)为发射波形自相关函数。对于不同发射波形，其自相关函数近似相等。ccross(l,r)为由发射波形互相关函数引起的向量，(l,r)为噪声e(t,l)经过匹配滤波后的输出。注意，对于快时间编码MIMO，μ=1，l∈{}1,2,…,L；对于慢时间DDM-MIMO，由于多普勒滤波，我们有μ=M，l∈{1,2,…,L/M}。

把式（24）沿着慢时间维向量化，得到

式中，

由式（25）可见，匹配滤波后，MIMO 雷达阵列信号模型类似于传统的相控阵脉冲多普勒雷达阵列模型。b(θ0)⊗a(θ0)为空域导向向量，g(fd)为时域导向向量。不同之处在于MIMO 雷达阵列信号模型中增加了由于发射波形互相关引起的干扰项(r)。

距离维匹配滤波后的信号处理在无杂波情况下，可使用时域和空域匹配滤波，实现目标成像，获得目标距离-角度-多普勒参数估计。其具体实现步骤如下。首先对第l个脉冲的M个天线数据构成的向量y（l,r）进行空域匹配滤波，可以获得

式中，θ为待搜索空间区域内的角度值。

定义空域滤波后的向量ys(r,θ)为

对ys(r,θ)按照式（28）进行时域滤波，即可得到目标成像结果yst(r,θ,f)。根据式（28）的成像结果，可实现目标距离-角度-多普勒参数估计。

式中，f为待搜索多普勒范围内的值。

在杂波情况下，可以使用空时信号处理STAP（Space-Time Adaptive Processing）实现杂波抑制和运动目标探测［62-63］，其实现公式如下：

式中，

μ1为常数，Rc+n(r)为在r距离单元处的杂波与噪声协方差矩阵，实际中可利用临近距离单元的回波对其进行估计。

2.3 仿真结果

MIMO 雷达仿真平台参数设置如下：载波频率为500 MHz，发射脉冲信号带宽B=1 MHz、脉冲宽度为100 μs，脉冲重复周期Tr=0.003 s，平台飞行速度为50 m/s。发射阵元个数为2，接收阵元个数为4，发射阵元间距为2λ，接收阵元间距为0.5λ，λ为发射信号波长。发射阵和接收阵布放方式如图1所示。目标的归一化多普勒频率为fdTr=0.1，归一化空间频率为-2.5。

只存在运动目标情况下，机载MIMO雷达接收数据利用三维匹配滤波（包含距离维压缩、阵元维波束形成和脉冲维FFT）得到成像结果。快时间Up-down Chirp FDM-MIMO 波形的探测结果如图11所示，快时间CAN CDM-MIMO 波形的探测结果如图12所示，慢时间DDM-MIMO 波形的探测结果如图13所示。

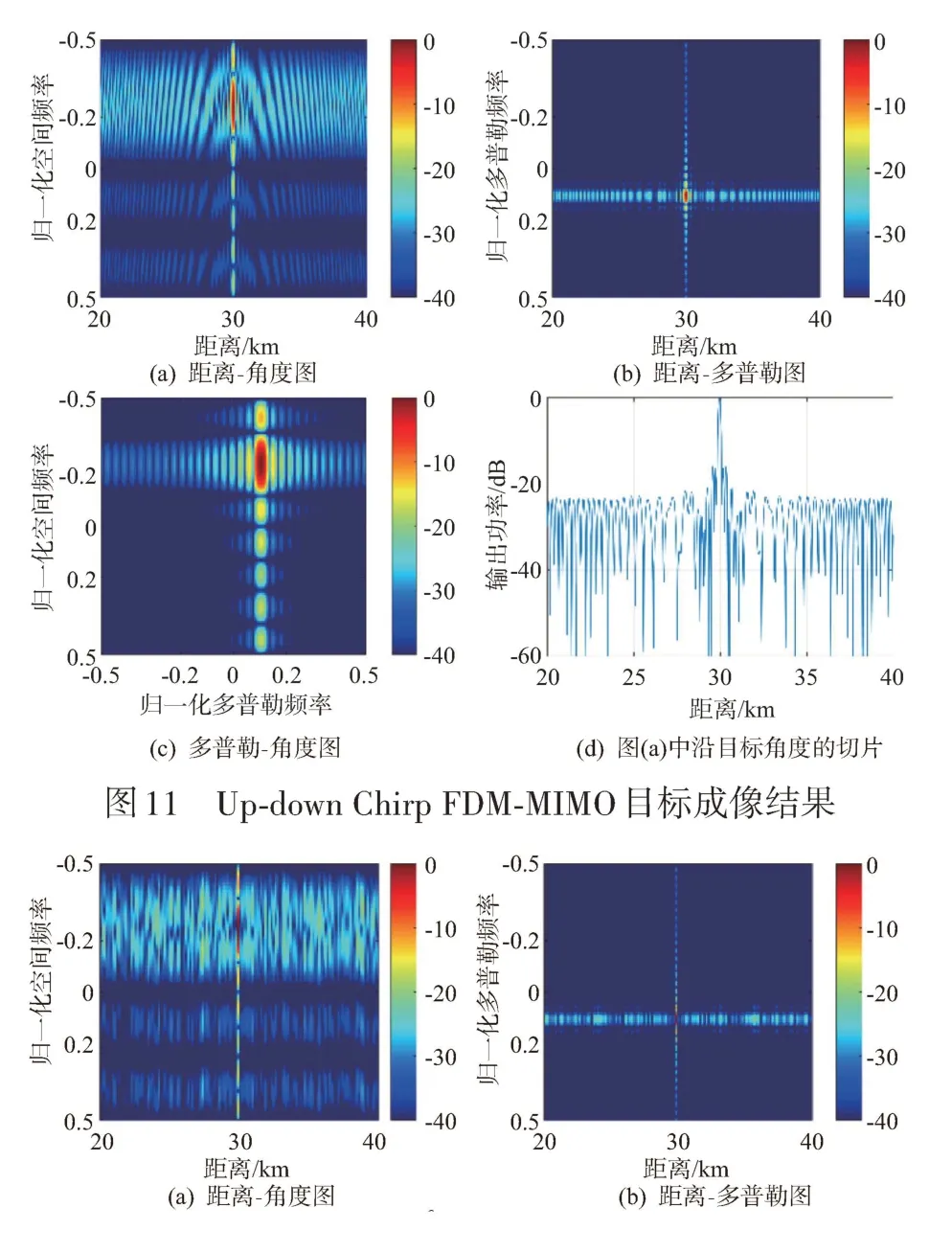
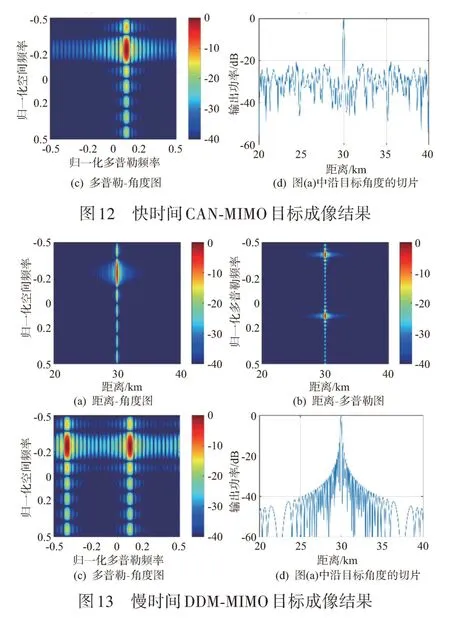
对比图11和图12不难发现，快时间Up-down Chirp FDM-MIMO 波形与快时间CAN CDM-MIMO的距离旁瓣类似；快时间Up-down Chirp FDMMIMO 波形的平均距离旁瓣为-29.3 dB，略微高于快时间CAN CDM-MIMO 的距离旁瓣（-31.7 dB）。另外，两种波形的多普勒旁瓣类似。这是由于这两种波形都使用了快时间编码实现不同发射波形在脉冲内的正交性，而同一发射波形在不同时刻发射相同脉冲，从而可以获得理想的多普勒滤波结果。再者，两者的距离旁瓣较高，这是由于它们都使用了脉冲内快时间编码实现发射波形分离。

从图13可见，DDM-MIMO 的距离旁瓣与标准LFM 信号距离旁瓣相同，其平均距离旁瓣为-45.1 dB，与上面两种快时间编码波形相比，降低15 dB左右。这是因为DDM波形利用多普勒域分离多个发射波形，每个脉冲都是标准的LFM 波形。另一方面，由于对多普勒域资源的利用，导致DDM-MIMO成像结果存在多普勒模糊。

3 MIMO雷达发展态势与应用问题

3.1 相控阵-MIMO混合雷达［64-68］

与相控阵雷达相比，MIMO 雷达发射端发射正交波形的代价是其发射信号功率下降了M倍。相控阵-MIMO 混合雷达发射端由多个相控子阵组成，子阵之间发射相互正交的波形，子阵内部天线发射相干波形，其示意图如图14所示。

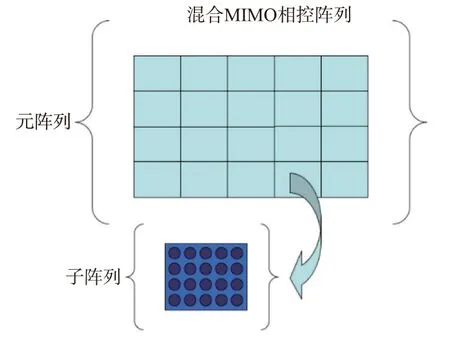
图14 相控阵-MIMO混合雷达示意图［65］

相控阵-MIMO 混合雷达同时具有相控阵和MIMO 雷达的优点，可以获得高增益发射波束。但相控阵-MIMO 雷达涉及复杂的子阵系统，难以实现。文献［68］通过在发射端和接收端，利用RF 波束形成技术实现相控子阵，极大降低了MIMO通道数目，便于系统实现。而且文献［68］实现了16 阵元相控子阵2×2 MIMO 雷达系统，其角度分辨率小于1°。

3.2 MIMO雷达稀疏信号处理

传统MIMO 雷达信号处理基于匹配滤波器理论，通过线性匹配搜索获得目标参数（位置、角度、运动速度等）。在图像处理领域发展起来的稀疏重构理论利用数据模型的稀疏性，在约束重构误差条件下，利用l0或者l1范数选取最稀疏的数据模型，从而获得数据模型的参数估计值［69-70］。在雷达探测中，由于目标的天然稀疏性，稀疏重构方法可以用于快时间域、慢时间域、空域或者它们之间的联合域，估计不同的目标参数。在文献［71］，稀疏重构理论被应用于时频联合域，同时估计目标距离和运动速度，理论分析证明稀疏重构方法可以获得比传统匹配滤波方法更高的参数估计精度。文献［72-73］研究表明在严格正交发射波形条件下，稀疏重构理论应用于MIMO 雷达时，可以降低目标成像的距离旁瓣。文献［74］在不严格正交发射波形下，利用联合块稀疏理论实现了低距离旁瓣的MIMO 雷达成像。文献［75］进一步考虑杂波情景与MIMO雷达发射波形不完全正交时，利用距离-多普勒域的二维块稀疏重构实现了杂波场景下微弱动目标探测。文献［76］将稀疏重构理论应用于空域，并与四阶累计量相结合，解决了在阵列互耦情况下的MIMO 雷达测向问题。同样，文献［77］将稀疏重构理论应用于空域，并利用互协方差稀疏重构解决了多径信号条件下MIMO 雷达对低空目标仰角估计的估计问题。文献［78］研究发现对于dithered DDMA 波形，在接收端利用稀疏信号处理，可以显著降低多普勒旁瓣。

与匹配滤波器的线性运算不同，稀疏重构算法是非线性运算，其提升了参数估计精度的同时也增加了计算复杂度。因此，目前稀疏重构算法在MIMO 雷达中只处于理论研究阶段。随着计算能力的不断提高，在不远的将来，基于稀疏重构理论的MIMO 雷达信号处理技术有望在实际系统中成功应用。

3.3 杂波情况下的运动目标探测性能

大部分文献针对纯净目标的互相关特性，设计MIMO 发射波形。但在机载雷达应用中，MIMO雷达接收回波中，不可避免地存在大量地面回波。每个地面回波在每对MIMO 雷达发射之间必然都存在互相关，即使此互相关很小，由于地面回波数量众多，所有回波的互相关叠加量仍然很可观。这些杂波互相关在天线主瓣处造成虚警，从而影响运动目标探测［79］。

文献［80-81］综合考虑目标和杂波的统计特性以恒模和相似性约束，设计MIMO 发射波形，获得最优的信杂噪比改善。文献［82-83］通过联合设计发射波形和接收端信号处理，抑制与目标信号相关的杂波。

3.4 互相关函数下界

已有文献探索频域、时域、码域自由度设计互相关尽可能小的MIMO雷达发射波形。但是，鲜有文献探索发射波形互相关函数的下界。互相关函数下界可以给MIMO发射波形设计提供方向，探究所设计的MIMO 发射波形互相关函数与互相关函数下界的差距，并利用互相关函数下界中的主要因素指导MIMO 发射波形设计。文献［84］分析了具有平滑幅度频谱的FDM-MIMO 发射波形互相关理论下界，指出互相关下界的平均值与最大值都与时宽带宽积有关，并提出一种FDM-MIMO 波形集设计方法，其互相关接近理论下界。文献［85］对CDM-MIMO 波形设计的互相关下界归纳总结，包括相关函数峰值旁瓣下界、相关函数积分旁瓣下界、互相关内积下界、互补序列相关函数下界四大类。文中指出相关函数峰值旁瓣下界是影响MIMO 雷达波形增益的关键指标。典型相位编码波形相关函数指标与下界的对比结果表明，目前CDM-MIMO 波形集互相关与已有下界的差值较大，尤其在波形数较多情况下。CDM-MIMO波形集相关函数下界仍是一个有待继续完善的开放问题。

4 结束语

MIMO 雷达经过近20年发展，理论日趋成熟。但是，目前MIMO雷达大部分理论性能是基于发射波形集严格正交得到的，因此，讨论MIMO 雷达发射波形的正交性非常关键。实际上，在不牺牲时域/频域资源情况下，受限于时宽带宽积，工程应用中并不存在完美正交的发射波形，发射波形之间总是存在互相关。即使互相关很小，在杂波场景下，所有杂波的互相关叠加仍会造成目标探测性能的严重下降。本文论述了三类快时间波形复用技术，包括TDM、CDM 与FDM 波形设计方法；同时，论述了慢时间波形复用技术，包括DDM与慢时间随机编码波形设计方法。基于单目标情况，简要概述MIMO雷达的统一信号处理框架。

仿真结果展示了基于快时间CDM、快时间FDM、慢时间DDM 的目标成像性能。仿真结果表明，由于脉冲内编码，快时间编码波形的距离旁瓣较高；而慢时间编码波形的距离旁瓣低。但是，慢时间DDM 波形存在多普勒模糊的缺点。因此，要综合各种波形的优缺点和实际应用需求，选择合适的波形设计方法。

最后，针对MIMO 雷达波形设计中的问题，综述了当前的研究热点和解决方案。