基于多图像特征的幼龄沉香全氮估测

袁 莹,王雪峰*,王 甜,陈飞飞,黄川腾,林 玲,董晓娜

(1.中国林业科学研究院资源信息研究所,国家林业和草原局森林经营与生长模拟重点实验室,北京 100091;2.海南省林业科学研究院,海南省红树林研究院,海南 海口 571100)

沉香(土沉香,Aquilariasinensis)又名白木香,喜生于海拔较低的山地丘陵地带,主要分布在广西、海南、广东、福建等地[1],是我国特有的珍贵濒危树种。沉香具有极高的药用价值,具有止痛、止呕、抗肿瘤活性等功效[2]。由于具有十分显著的经济效益,沉香天然林在乱砍滥伐中愈加稀少,但其市场需求量不减反增。近些年来在广西、海南等地沉香苗木的人工培植规模日益增大[3],与此同时,鉴于该树种的珍贵特性,在其生长发育过程中如何在非破坏前提下对其营养信息进行估测成为近年来亟需解决的重要议题。氮素是蛋白质和叶绿素的组成成分,是影响林木生长发育的最重要的营养元素之一[4],植物叶片的氮含量能够反映植物整体的生长态势和营养状况。氮素的缺乏和过剩均会影响植物的生理生化机制[5],因此,对氮素进行有效监测是对沉香苗木进行合理培育经营的重要基础。经过国内外学者们的研究发现,图像信息与植物的生长、生理状态有着紧密联系[6]。相较于传统的化学测定方法,结合数字图像处理方法对林木营养进行监测大大提高了时效性[7],且减少了对林木的破坏。

有效利用具有代表性的图像特征是建立沉香氮素估测模型的重要基础[8],植株叶片的氮素含量在冠层颜色上有较为清晰的体现,图像的形状特征则可以较好地反映沉香植株的生长特性[9],而当氮含量发生变化时,图像的纹理特征也会发生一定的变化[10-11]。吴伟斌等[12]确定了基于高光谱图像特征对茶树氮含量和叶面积指数(LAI)进行反演,获得了较高的模型精度,但成本相较于数码相机获取可见光图像较为高昂。张培松等[13]对利用数码相机获取的橡胶树叶片图像提取多个颜色特征,对橡胶树叶片氮含量进行营养诊断,但未对颜色特征以外的其他图像信息进行分析。因此,以幼龄沉香全氮量为响应变量,获取沉香冠层可见光图像,对图像的颜色、纹理、形状特征进行综合分析具有一定的实际意义。

在基于图像特征构建营养状态估测模型时,Agarwal等[14]应用主成分分析(PCA,Principal component analysis)对叶片图像的颜色特征进行降维,避免了高维图像特征数据带来的维度灾难和多重共线性问题,再对叶片养分和叶绿素含量构建多元线性回归估测模型;Lucas等[15]应用随机森林算法对柑橘树冠层氮含量进行了估测,并与其他机器学习算法进行了对比分析;Amirruddin等[16]构建线性判别和支持向量机模型基于图像光谱数据对油棕氮营养状态进行分类。

本研究以幼龄沉香为研究对象,基于色调-亮度-饱和度(HIS)空间的最佳直方图(KSW)熵法对沉香冠层图像进行分割提取,提取沉香数字图像的多种颜色、形状和纹理特征,通过偏最小二乘法(PLS)有监督地降维融合对沉香图像的多特征进行综合利用,并应用天牛须搜索算法(BAS)实现模型参数的自适应选取,以多图像特征为基础构建PLS-BAS-ElmanNN模型对沉香叶片全氮量进行无损估测,探索了利用图像估测沉香营养状态的新方法,以期为实现沉香苗木培育的精准作业提供理论依据。

1 材料与方法

1.1 研究区概况

研究区设在海南省文昌市龙楼镇的岛东林场昌洒作业区(110°57′34″～111°1′54″E,19°43′58″～19°44′58″N),海拔5～20 m。岛东林场占地约1.9万hm2,东临南海,属沿海平原地带,地势较为平缓,森林资源丰富,为热带海洋性气候,气温年较差较小,年均气温23.5 ℃,年均降水量约1 808.8 mm。试验地土壤类型为滨海沙壤土,土壤pH为5.0～6.6,有效氮含量98.3～114.8 mg/kg,有效磷含量3.38～4.56 mg/kg,速效钾含量69.9～ 78.2 mg/kg,有效铁含量2.33～4.89 mg/kg。

1.2 数据采集

图像获取设备为CanonEOS750D相机,传感器为CMOS,传感器尺寸22.3 mm×14.9 mm,有效像素约为2 420万,APS-C画幅。将沉香盆栽置于转台,盆栽上方放置带孔隔板以达到简化图像背景的效果,对沉香植株进行侧方位摄影和上方位俯拍(图1)。俯拍时应确定相机垂直于地面,避免产生倾斜误差,侧方拍摄时应通过转动转台的方式拍摄东南西北4个方位的沉香图像。试验材料为研究区域中生长的54株健康无病虫害的幼龄沉香苗木,通过在沉香冠层的上、中、下层分别各摘取4～8片叶片测定全氮含量代表沉香整株叶片的全氮含量。单株沉香摘取的叶片烘干后通过H2SO4-H2O2消煮法进行全氮含量测定,最终获得沉香叶片全氮含量最小值为10.3 g/kg,最大值为25.6 g/kg。

图1 沉香植株拍摄方位示意图Fig.1 A schematic diagram of shooting orientation for Aquilaria sinensis

1.3 图像处理

图像分割是根据图像的灰度、颜色、纹理等特征[17]将植株目标从背景中分离出来,是图像分析工作的基石。本研究将KSW熵阈值分割和形态学处理相结合完成沉香图像的分割,其中KSW熵阈值法是以图像信息熵为准则进行分割的方法,计算速度快且分割效果较好,为最常用的分割方法之一,形态学处理包括腐蚀和膨胀,可以依此除去目标边缘的少量散布背景点。KSW熵阈值分割原理是设阈值t将图像分为目标和背景两类,记为T0和T1,则T0和T1熵的计算公式分别为:

(1)

(2)

令H(t)=H0(t)+H1(t),即为图像的总熵,遍历所有可取的阈值t,其中令H(t)取得最大值的对应t值即为所求的分割阈值。

1.4 特征提取

1.4.1 颜色特征

在计算机处理下的图像色彩特征值更能够反映出人类肉眼难以辨别的差异。对于数字图像而言,RGB是最常用的颜色空间,通过一定的公式也可以转化为HIS、Lab颜色空间等,提取图像的多通道值作为色彩特征,通过对这些色彩特征的组合运算可获得多种色彩特征[18]。

1.4.2 纹理特征

灰度差分统计(GLDS)是最常用的提取图像纹理的方法之一,令图像中的一点与其相邻点的灰度差值为Δg,称为灰度差分。通过图像直方图获取Δg相应的概率,计算得到均值、对比度、熵等特征。GLDS计算简单,效率较高,但仅能分析图像整体纹理特征。灰度共生矩阵(GLCM)通过研究灰度的空间相关性来描述纹理,能够提取灰度关于方向、相邻间隔、变化幅度的综合信息。常用的纹理特征有能量(二阶矩)、惯性矩、相关性、熵等。

1.4.3 形状特征

此前学者们对不同营养状态的植株图像分析主要集中于颜色和纹理特征上[18],事实上氮素缺乏或过剩对植株的生长所造成的差异也不容忽视。本研究提出了外接矩形法来获取图像形状特征,以矩形的长(H)、宽(W)和长宽比(r)反映植株的株高和冠幅信息,以冠层面积(Sa)和矩形度(e)作为体现植株冠层密闭度的参数。将固定大小的花盆直径引入计算,可避免摄影距离差异产生的误差。各形状特征的定义如下:

(3)

(4)

r=W/H;

(5)

Sa=S0/d;

(6)

e=S0/A。

(7)

1.5 模型构建

1.5.1 Elman神经网络

Elman神经网络(Elman neural network,ElmanNN)相对于反向传播神经网络(back-propagation neural network,BPNN)在网络结构中加入了承接层,使其能够对过去时刻输出的信息进行反馈,不仅解决了BPNN模型中的局部最小值陷入和计算速度慢的问题[19],还具有短期记忆功能,能够对样本进行动态预测。设有n个输入,m个输出,模型结构如图2所示。

图2 ElmanNN结构Fig.2 The structure of Elman neural network

ElmanNN的非线性状态空间表达式如下:

x(k)=f(ω1xc(k))+ω2u(k-1);

(8)

xc(k)=αxc(k-1)+x(k-1);

(9)

y(k)=g(ω3x(k))。

(10)

式中:x(k)、x(k-1)分别为k时刻和k-1时刻的隐层单元值;ω1为承接层到隐含层的连接权值;ω2为输入层到隐含层的连接权值;ω3为隐含层到输出层的连接权值;u(k-1)、y(k)、xc(k)分别为k-1时刻和k时刻输入、输出和隐层输出;α为参数;f函数和g函数分别为隐含层和输出层的传递函数。常用正切S型传递函数F(x)和线性传递函数G(x),函数表达式如下:

(11)

G(x)=x。

(12)

令yφ(k)为目标输出,将误差平方和定义为网络的目标函数E,计算公式如下:

(13)

1.5.2 模型优化及验证

BAS算法是根据天牛通过触须觅食的行为提出的优化算法,该算法在优化过程中不需要知道目标函数的具体形式,且并未利用相关梯度信息,使得计算过程十分简单高效,在寻优速度上具有优势[20],通过BAS算法可以自适应确定ElmanNN模型的最优参数。此外为了确定模型的准确性和稳定性,本研究以留出法对模型进行验证,将试验获取的54个样本中40个作为训练样本,14个作为检验样本。

2 结果与分析

2.1 幼龄沉香图像分割

由于HIS空间将色亮分离,与人类的视觉感知方式相似,本研究应用KSW熵阈值分割和形态学处理相结合的方法,基于图像的HIS空间对幼龄沉香的可见光影像进行分割。首先对沉香可见光图像进行阈值分割获得目标和背景的二值化图像,再对目标图像进行形态学腐蚀去除少量未能与目标分割开的背景点。考虑到此前有不少学者对不同颜色空间的图像分割方法进行了分析对比[21-22],但并无统一结论,将本研究应用的基于HIS颜色空间分割的方法与常用的RGB、Lab颜色空间进行对比,结果见图3。

A. HIS颜色空间分割结果 segmentation results based on HIS;B. RGB颜色空间分割结果 segmentation results based on RGB;C. Lab颜色空间分割结果 segmentation results based on Lab。

由图3可见,RGB和HIS空间分割均能较好地将植株分割出来,但在边缘的噪声处理上HIS空间获得了更好的分割效果,而Lab空间分割后的图像存在明显未除去的背景部分,沉香冠层的边缘并不明显。因此对于幼龄沉香而言,本研究应用基于HIS空间进行KSW熵分割的方法取得最优分割效果。

2.2 沉香图像特征提取

2.2.1 颜色特征

应用MATLAB软件对分割后的幼龄沉香图像进行特征提取,基于RGB、HIS、Lab颜色空间共提取得到9个颜色特征,对所有的颜色特征值进行统计整理后结果见表1。

表1 沉香图像颜色特征值

此外本研究还将得到的颜色特征进行组合,选取了13个特征组合,分别为R/B、G/B、B/(R+G)、R/(G+B)、R/(R+G+B)、B/(R+G+B)、G/(R+G+B)、(R-B)/(B+R)、(B+G)/(R+B+G)、(R-B)/(R+G+B)、G/(R-B)、B/L、G/L,作为全氮估测模型的输入数据。

2.2.2 形状特征

本研究提出以不同外接矩形的方式提取沉香植株侧面和冠层的形状特征。以沉香侧面图像为研究对象时,选取正外接矩形的方式获取形状特征,矩形的长和宽体现了植株的株高和冠幅,如图4A;以沉香冠层图像为研究对象时,选取最小外接矩形的方式获取沉香的形状特征,矩形的矩形度则反映了冠层的疏密程度,如图4B;对比传统的以正外接矩形获取矩形度的方式(图4C),采用该方法对于不规则的冠层形状能够更加稳定地反映冠层密闭度。

图4 外接矩形示意图Fig.4 Bounding rectangle

根据公式(3)—(7)计算得到图像的5个形状特征H、W、r、S、e,见表2。

表2 沉香图像形状特征

2.2.3 纹理特征

使用两种方法对幼龄沉香冠层图像提取局部和整体纹理特征,应用GLCM法计算得到能量(En)、熵(Ent1)、惯性矩(MOI)、相关(Cor)在4个方向上的均值(mean)和方差(std)。GLDS法计算得到均值(mean)、对比度(Con)、角二阶矩(ASM)、熵(Ent2),其中由于GLDS和GLCM计算原理不同,得到的熵值也不同,作分开标识。最终获取了12个纹理特征,见表3。

表3 沉香图像纹理特征

2.3 沉香叶片全氮量估测模型

2.3.1 PLS降维

为避免量纲的影响,将提取的39个图像色彩、形状和纹理特征值进行标准化处理。由于特征变量较多,会降低模型的计算能力,且变量之间若存在多重共线性也会影响模型的泛化性能。应用PLS算法对图像特征提取主成分从而完成特征的降维,以90%的方差贡献率为阈值提取了6个主成分,此时方差累计贡献率达到91%,见图5。沉香图像特征变量的维数由39降至6,被有效降低。

图5 主成分方差贡献率Fig.5 Variance contribution rates of principal components

对PLS降维前的图像特征变量和降维后的6个主成分分别进行相关性分析,结果如图6所示。图6A为降维前的相关性分析结果,部分图像特征变量之间存在强相关性,即具有多重共线性。图6B为PLS降维后的相关性分析结果,可以看到相关系数大大降低,6个主成分之间的相关系数均接近于0,不存在多重共线性。显然,本研究使用的PLS算法在图像特征变量的降维和消除多重共线性方面取得了显著效果。

图6 PLS降维前后特征变量及主成分相关性分析Fig.6 Correlation analysis of feature variables and principal component before and after PLS dimensionality reduction

2.3.2 BAS-ElmanNN全氮含量估测

将PLS提取的6个主成分作为估测模型的解释变量,构建BAS-ElmanNN模型,对幼龄沉香叶片全氮含量进行估测。以BAS算法实现Elman网络的训练参数的寻优,通过训练样本确定ω1等权值,使用已训练好的BAS-Elman模型对14个检验样本进行估测,模型估测结果见图7。图7中显示估测值与真实值相近,即本研究提出的BAS-ElmanNN模型估测效果较好,相关系数为0.860 7,RMSE为1.265 3 g/kg。

图7 BAS-ElmanNN模型估测结果Fig.7 Prediction results of the BAS-ElmanNN model

为进一步定量分析模型的精度和适用性,以决定系数(R2)、平均相对误差(MRE)、平均绝对误差(MAE)、均方误差(MSE)、均方根误差(RMSE)作为评价指标进行模型验证。此外将本研究提出的PLS-BAS-ElmanNN模型与多个常用的参数、半参数和非参数模型进行对比分析,以确定最适用于沉香全氮含量的估测模型。其中参数模型包括偏最小二乘回归(PLSR)、主成分回归(PCAR)和岭回归(RR)模型,半参数模型为以PLS 提取的6个主成分为解释变量构建偏最小二乘-广义可加模型(PLS-GAM),非参数模型包括以39个图像特征构建的ElmanNN、径向基神经网络(RBFNN,Radial basis function neural network)、BPNN模型和以6个主成分为解释变量构建的偏最小二乘-径向基神经网络(PLS-RBFNN)、偏最小二乘-BP神经网络(PLS-BPNN)模型。各模型评价结果见表4,其中PLS-GAM中各主成分的偏残差分析结果见图8。

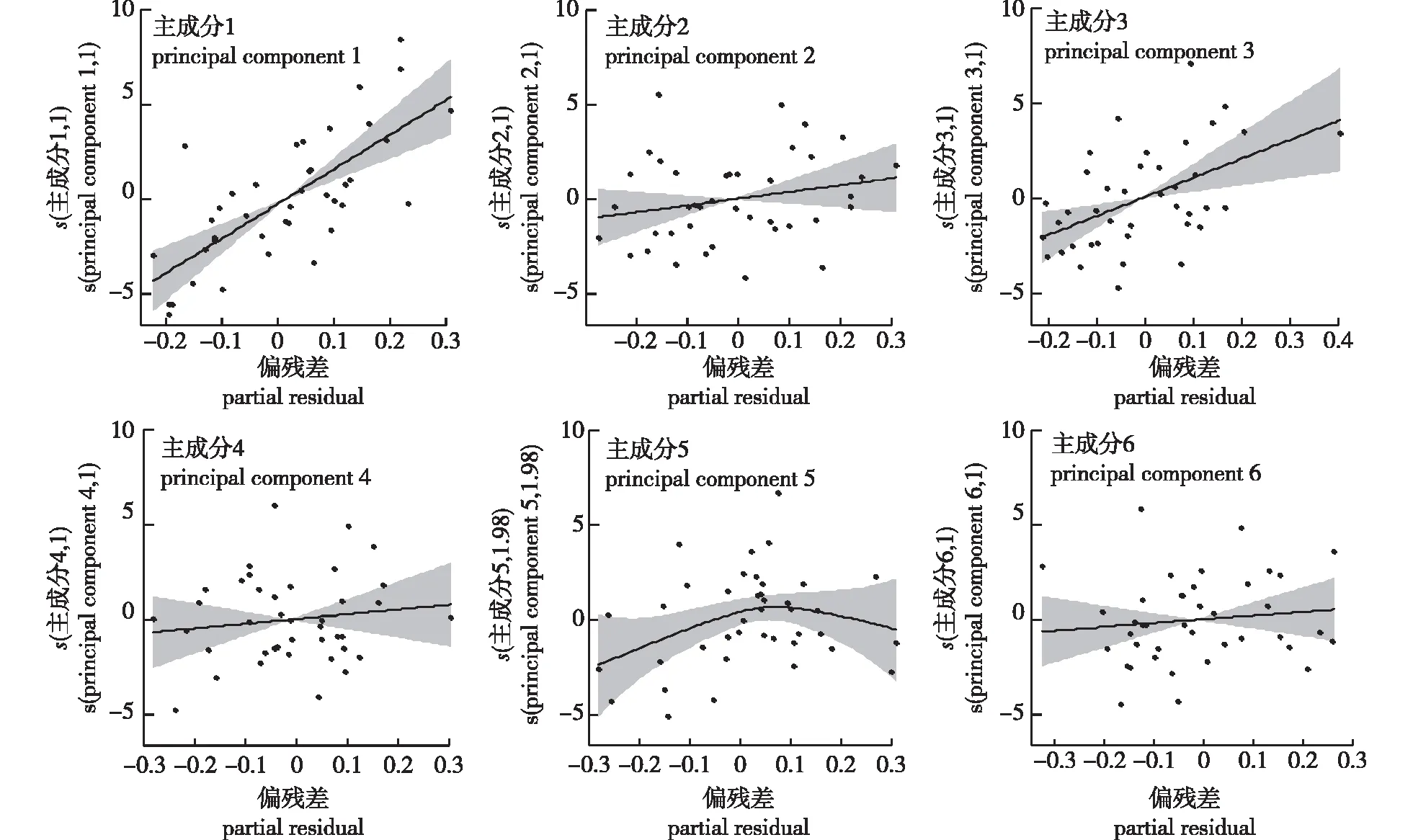
s表示平滑函数,s(主成分i,j)表示s(自变量, 自由度);自由度j为1时表示线性关系,大于1表示非线性关系。s refers to the smoothing function, s (principal,component i,j) refers to s (independent variable, degree of freedom), when the degree of freedom is 1, it indicates a linear relationship, and greater than 1 indicates a nonlinear relationship.

表4 模型评价与对比

由表4可知,在多种模型中,本研究提出的PLS-BAS-ElmanNN模型与PLS-GAM模型、PLSR模型的MRE均低于10%,取得了较好的沉香全氮含量估测效果。其中,PLS-BAS-ElmanNN模型的MRE最低,仅为6.0%,决定系数R2达到0.740 7,R2较PLS-GAM模型和PLSR模型分别提高了5.5%和18.5%,RMSE仅为1.265 3 g/kg,较PLS-GAM模型和PLSR模型分别降低了21.1%和27.2%。

此外,在非参数模型中,基于39个图像特征直接构建的ElmanNN、RBFNN和BPNN模型的估测效果均较差,难以对幼龄沉香全氮量进行准确诊断。基于PLS提取主成分后构建的PLS-RBFNN和PLS-BPNN模型虽在估测精度上有所提升,但依旧低于PLS-BAS-ElmanNN模型。因此,可确定本研究提出的PLS-BAS-ElmanNN模型为进行幼龄沉香叶片全氮量估测的最适模型。

由图8可见,在PLS-GAM半参数模型中主成分1、2、3、4、6的偏残差图均为线性,主成分5的偏残差图则表现了显著的非线性,可见PLS-GAM模型对非线性关系具有一定的解释能力,因此获得了较PLSR模型更高的估测精度。

3 讨 论

传统的叶片氮含量测定方法费时费力且具有破坏性,难以满足珍贵树种营养状态的监测需求,而经国内外诸多研究学者证明,计算机视觉技术是实现无损估测的有效方法[23-24]。应用计算机视觉方法估测叶片的全氮含量主要包括图像处理和估测模型构建两部分,在对植株图像的分割处理中,陈珠琳等[21]研究表明在HIS颜色空间下能够对檀香获得较好的分割效果,Bai等[25]论证了在Lab空间对植物图像进行分割提取的可行性,本研究应用的基于HIS颜色空间的KSW熵及形态学处理组合分割方法对幼龄沉香取得了最优分割效果,优于RGB和Lab空间分割,因此可认为基于HIS空间分割的方式更适用于沉香图像。其中,Lab空间分割效果最差,许多散乱的背景区域未能与目标图像分割开,这与Lab空间包含了过多的色彩信息反而难以很好地将背景完全剔除不无关系。而HIS空间接近于人类视觉,在自身视觉感知到前背景差异较明显的情况下,使用HIS空间进行图像分割通常能实现更好的分割效果。

将幼龄沉香的前景图像分割出来后,本研究提取了沉香图像的22种颜色特征、12个纹理特征和5个形状特征构建沉香全氮含量估测模型。在高维图像特征数据的处理中,相较于Agarwal等[14]应用的PCA方法,PLS算法结合了PCA和典型相关分析的优势,能够以沉香叶片全氮量为依据完成图像特征的降维,同时变量间的多重共线性也得到了有效解决。在模型的评价对比结果中,可以看到若对图像特征降维后获得的变量直接构建线性回归模型,即PLSR模型,其R2为0.624 9,较PCAR模型具有更高的估测精度,与Tang等[26]对PLS与PCA进行分析对比的研究结果具有一致性。这是因为PLS是一种有监督的降维方法,充分利用了沉香全氮含量信息,因此该方法提取的主成分对沉香全氮含量具有更高的解释能力,不论是精度、稳定性和实用性都优于传统的PCA降维方法。

在模型的验证分析中,通过R2、MRE、MAE、MSE、RMSE这5个评价指标对比,可确定本研究提出的PLS-BAS-ElmanNN模型估测精度最高,其次为半参数模型PLS-GAM和参数模型中的PLSR模型。在非参数模型中,基于PLS算法提取主成分构建的沉香全氮含量估测模型的估测效果显著优于基于39个图像特征直接构建的模型,这是由于当输入的解释变量过多且变量之间具有多重共线性时训练数据易出现过拟合现象[27],导致模型泛化能力低,因此在使用检验样本进行模型验证时获得了较差的验证结果。而对比其他基于PLS算法的神经网络模型,如PLS-BPNN和PLS-RBFNN模型,本研究模型的估测精度也具有显著优势,因此可确定在本试验中,ElmanNN相较于其他神经网络更适用于沉香叶片全氮含量的估测。此外,在参数和半参数模型对比中,本研究提出的PLS-BAS-ElmanNN模型、PLS-GAM模型和PLSR模型均获得了较好的估测效果,PLS-GAM的偏残差图中可以看到主成分5的偏残差图具有显著的非线性,而本研究模型为非参数模型,二者对非线性数据具有更好的拟合效果,因此较线性模型PLSR精度略高,但PLS-GAM模型精度依然低于本研究模型。且根据图8可以看到其他主成分均与沉香全氮含量存在线性关系,这也是本研究模型和PLS-GAM模型比PLSR模型估测精度提升幅度较小的主要因素。

4 结 论

1)对于幼龄沉香图像,基于本研究应用的HIS颜色空间下应用KSW熵和形态学处理进行分割,分割效果显著优于RGB和Lab空间。

2)对于存在多重共线性的高维图像特征变量,PLS算法以沉香叶片全氮量为依据对特征变量提取了6个主成分,快速降低了特征变量维数,并有效避免了变量间多重共线性影响。

3)以5种模型评价指标对本研究提出的PLS-BAS-ElmanNN模型进行验证,并与多种常用的参数、半参数和非参数模型进行对比,本研究提出的模型R2达到0.740 7,MRE值为6.0%,RMSE值为1.265 3 g/kg,综合比较下估测精度最高,优于其他模型,为适用于幼龄沉香全氮量估测的最优模型。