体验式教学在小学数学求图形阴影面积中的应用研究
朱斯媚


摘 要:新课标(2022)指出,课程目标以学生发展为本,以核心素养为导向进一步强调学生获得“四基”,发展“四能”,形成正确的情感、态度和价值观。体验式教学使学生在亲历的过程中理解并构建知识、发展能力、产生情感、生成意义。强调的是“以人为本”,使学生真正成为学习的主体。体验式教学作为新课改大背景下的创新教学策略与新课标的课程目标不谋而合。由此也说明体验式教学在课堂教学中有着举重轻重的现实意义,接下来本文将以求图形的阴影面积为例对体验式教学进行应用研究。
关键字:体验式教学;图形的阴影面积;几何画板;量感;推理能力
一、在数学课堂中实施体验式教学的意义
学生是课堂活动中学的主体,学生的兴趣维持在怎样的水平直接关系到课堂教学的效果,有效的教学不是教师灌给学生的,而是学生自己体验得到的。一旦学生的学习兴趣被有效调动,那么,数学概念、公式、原理都变成一个个美丽的符号,课堂上会积极地配合教师的各项互动活动,主动地学习。
二、如何在课堂中渗透体验式教学
《数学教学改革指导纲要》指出在图形测量计算的教学过程中要遵循和体现学生形成关于图形计算的认识过程,即在教学中要注意先是渗透最上位的的思想和策略,再是引导学生理解和把握图形计算问题解决中一般方法和特殊方法的原理,最后才是末端的根据原理的具体算法的掌握。
图形阴影面积的计算方法与规则的基本图形的基本思路或方向上具有共同的一致性,这就是所谓的上位思想和策略。其突破点在于让学生理解和把握解决问题的一般方法和特殊方法的原理,而这一部分就需要学生进行体验式学习。
帕克·巴默尔(Parker Palmer)说:“深入而持续的体验对我们的影响最大,在我们自己的身体和意识中留下了持久的烙印。而图形的阴影面积属于抽象的知识,学生缺乏生活的实际感知,只能通过公式、原理进行说理,形成具体算法,大多数学生听完后都是一知半解,变换一下图形的位置,或者转换一下基本图形的形状,学生就无法发现他们共同的解题思路与原理,所以越是抽象的知识,越需要学生进行体验式的学习,教师也有义务对这些知识进行体验式的教学。而在求图形阴影部分面积如何渗透体验式教学,本人认为应从以下三方面入手。
(一)“读图”,理清图形各部分之间的关系
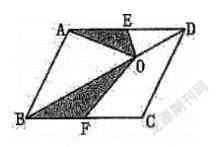
1.如图,平行四边形ABCD 的面积是48c㎡,0是对角线上一点,且点 E、点F分别是 AD、 BC 的中点。求阴影部分的面积。
读图要点:O是对角线的任意一点,O的位置变化是否影响阴影部分的面积,如果是,阴影部分会随着O点的变化如何变化。
2.如下图,正方形ABCD的边长为6厘米,三角形ABE,ADF与四边形AECF的面积相等,那么三角形AEF的面积是多少平方厘米?
读图要点:点E、F的位置是否固定,如果不固定可以怎样变化,变化后图形的哪些部分会改变,哪些部分不会改变,这些“变”与“不变”对阴影部分的面积会产生什么样的影响。
3.如图,两个完全一样的梯形重叠在一起,求阴影部分的面积。(单位米。)
读图要点:阴影部分的面积是否可以利用公式直接求得,如果不行,可以进行怎样的转化。
(二)利用幾何画板操作,体验图形的“变”与“不变”,初步猜想算法
第一题根据题目要求,利用几何画板精准作图,作出面积为48m2的平行四边形,把点E与F定点出来,点O设置为动点,把求两个阴影图形面积的底跟高度量出来,根据动点的移动,让学生观察数据的变化,不断地让动点移动,学生可以发现不管O点怎么移动,两个阴影图形的高始终等于平行四边形的高,阴影部门的面积始终的24m2。
初步猜想算法:因为两个阴影面积的底相加刚好等于平行四边形的底,高相加刚好等于平行四边形的高,所以阴影面积之和等于平行四边形的一半,就是24m2。
第二题在几何画板上任意作图,画出正方形,以及三角形ABE,ADF与四边形AECF,通过动点演示,发现如果随意给E、F定点,不管怎么移动,三角形ABE与三角形ADF的面积都不会相等,初步猜想点E、F是定点。
由已知条件正方形ABCD的边长为6厘米,三角形ABE,ADF与四边形AECF的面积相等,可知三角形ABE,ADF与四边形AECF三部分把整个正方形进行了三等分,可算出每一份是36÷3=12(cm2)。而三角形ABE,ADF是两个完全相等的三角形,所以可以确定出底是12×2÷6=4(cm)。根据已知信息可利用几何画板精准作出图形。
知道了各边的长度,利用EC=2cm,FC=2cm可以算出三角形ECF的面积为2×2÷2=2(cm2),再用12-2=10(cm2)。利用几何画板的精准作图计算,我们也可以验证三角形AEF的面积是10cm2
第三题利用几何画板作图,在操作的过程中发现,任意作图无法实现满足所有条件,让学生感知,知识的关联是相互的,数学的数据是严谨的。
在进行求阴影面积的解题思路中,发现哪怕用割补法转化成规则图形直接用公式求阴影的面积,给出的数据条件依然不够,这就需要转变思路,放眼全图,看看各部分之间存在怎样的等量关系可以利用,这时需要培养学生的量感,在整图中,猜测阴影部分面积可能等于重合梯形的面积,也有可能等于剩余梯形的面积,而在计算的过程中,发现利用几何画板的精确计算,剩余的面积与阴影部分的面积相等,这样我们就可以把问题转化成求剩余梯形的面积,而剩余梯形的面积根据公式可以直接代入数据得出结果。
(三)升华思想、发展量感与推理能力
以上三个图形的计算都利用了几何画板准确、动态地表达了几何现象,让学生在直观的体验图形的变化过程中,感受其变化规律。
经过三个不同图形的直观体验,培养学生从特殊到一般的数学思想方法,通过追问如果改变动点的位置,或者改变数据的大小,还能得出一样的结论吗?以此培养学生对图形面积大小的量感,以及发展学生的来推理能力。
通过几何画板的再次动态演示,让学生直观感受图形变化后的“变”与“不变”发现动点的变动,以及数据的改变,结论依然成立。
结语
新课标指出在图形的测量与计算的教学过程中,要实现让学生感悟数学度量方法,逐步形成量感与推理能力。这两方面能力都属于抽象能力,很难量化,习得需要学生有生活经验或者体验,而抽象图形的生活经验比较难取得,这就需要教师在课堂上搭建平台让学生进行体验,几何画板的直观体验式教学就解决了这一问题。
体验式教学并非是学生个体的自学,而是个体在自主探究的基础上形成自己的见解与观点。几何画板的图形体验式教学,让学生在深刻的动态演示中,体验图形的变化,感受图形的“变”与“不变”,形成量感,并在不断的“变”与“不变”中总结出普遍的变化规律,除了让学生感受从特殊到一般的数学思想方法外,还让学生习得一定的推理能力。
参考文献:
[1] 义务教育数学课程标准. 北京师范大学出版社,2022
[2] 吴亚萍. 数学教学改革指导纲要. 福建教育出版社,2017
[3] 缪亮,盘俊春. 几何画板5X课程制作实用教程:微课版,2018

