基于NSGA-Ⅱ的自适应多尺度特征通道分组优化算法

王 彬，向 甜，吕艺东，王晓帆

（1.西安理工大学 计算机科学与工程学院，西安 710048；2.陕西省网络计算与安全技术重点实验室（西安理工大学），西安 710048）

0 引言

卷积神经网络（Convolutional Neural Network，CNN）在计算机视觉领域，如医疗［1］、人体识别［2-3］、智能驾驶［4-6］、生物医学图像识别［7-8］、农业图像处理［9-10］等被广泛应用。随着CNN研究的不断深入，其网络结构的复杂度也随之增加，导致因计算效率降低而难以移植到计算能力受限的设备中。因此，在无法搭载较强计算能力硬件的设备上，如何继续保持CNN的特征提取能力成为值得研究的课题。

近些年，轻量化CNN 技术［11-13］得到逐步发展，可简要概括为针对网络结构冗余问题提出的模型压缩和针对性能退化提出的模型重构两大类［14］。模型压缩主要包括知识提取、网络剪枝、权值转化等［15-17］，旨在保持或稍微降低精确度的情况下提升网络计算效率。模型重构主要指重新设计轻量型卷积神经网络（Lightweight CNN，LCNN）结构，例如利用深度可分离卷积或分组卷积构建新的LCNN 结构，以提高CNN 的计算效率。尽管这些LCNN 在计算效率方面取得了不小进步，但仍不可避免地出现精确度退化情况，如何优化LCNN 结构成为亟待解决的问题。目前，一些先进的LCNN结构都是由具有领域知识的研究者手工设计的，因此会存在该网络结构设计并不能有效解决当前机器学习任务的问题，这在一定程度上会弱化网络的性能表现和泛化能力。近几年，进化算法（Evolutionary Algorithm，EA）在深度卷积神经网络的结构优化中得到应用，能提升优化后的网络性能。

EA 是一种受生物演化过程启发的全局优化方法，由于它的应用领域具有不受问题性质限制的特点，在深度学习等领域得到了应用和发展。经典的进化算法启发于模仿生物界种群更新的方式，通过变异、高斯交叉和选择的过程，在连续或离散的决策空间中高效搜索最优解。多目标算法的目标是求出一组各个目标之间权衡关系的近似的帕累托（Pareto）最优解集。常见的多目标进化算法包括三类：基于Pareto 支配关系的快速非支配排序遗传算法［18-21］等；基于分解的多目标进化算法［22］等；基于指标的多目标进化算法［23］等。2018 年，Wang 等［24］使用网络协议地址编码，采用的适应度函数为每批精确度平均值，同时使用随机划分数据集的方式加速适应度评估，提出了基于变长粒子群优化的神经网络结构。该方法试图利用粒子群算法自适应堆叠卷积神经网络模块，已经无须人工干预便可设计出解决图像分类问题的CNN 结构。由于超参数优化问题是非凸且不可微的，并且完整训练整个网络所需时间长，因此不必知道整个训练过程的最佳网络性能。出于该动机，Sun 等［25］利用粒子群算法网格化地搜索自动堆叠网络模型最匹配优化任务的超参数，显著降低了网络模型计算复杂度。他们设计了一种超参数优化方法，用堆叠自适应编码器执行了192 个实验对比，堆叠自适应编码器是一类具有较少超参数的深度学习算法，旨在研究进化算法和网格搜索在搜索堆叠自适应编码模型的最优超参数时的性能。2019 年，Lu 等［26］提出的高级神经体系结构搜索方法将误差度量（指标为图像分类正确率）和计算复杂度（指标为每秒浮点运算次数（FLoating-point Operations Per second，FLOPs）作为待优化的两个目标函数，经过种群初始化、探索和开发三个步骤，有效探索了有潜力的神经网络结构空间。这些基于EA 的深度卷积神经网络在一定程度上实现了不依赖专业知识和人工干预来优化提升网络结构性能的目的。

本文针对LCNN 结构的复杂度和精确度优化不平衡问题，进行双目标函数建模及分析，提出基于NSGA-Ⅱ的自适应多尺度特征通道分组优化算法，构建基于NSGA-Ⅱ的自适应多尺度的特征融合网络NSGA2-AMFFNetwork，并在图像分类数据集上验证了优化算法的有效性。

1 相关工作

1.1 非均匀通道分组

LCNN 的参数量和计算量随着其复杂度的提升而增加，影响了LCNN 的计算速度。2020 年，笔者在M_blockNet_v1结构中提出了基于非均匀通道分组多尺度的特征融合方法（图1）［27］，以进一步降低参数量和计算量。

图1 非均匀通道分组多尺度特征融合Fig.1 Heterogeneous channel grouping multi-scale feature fusion

图1 中，LCNN 的特征融合采用基于膨胀卷积的多尺度特征融合模块代替原有的1 × 1 点卷积的特征融合；然后，将输入特征图通道分成G组，其中，1 × 1 点卷积、3 × 3 基本卷积以及3 × 3 膨胀卷积操作对应的输入和输出通道数分别为g1、g2和g3；最后，连接不同尺度通道提取到的特征图得到最终的输出特征图，以减少计算量和参数量。该方法中，每个尺度的卷积核输入仅包含部分的输入特征图，目的是减少参数量以及运算量，但该方法需要手动设计和寻找相关的合适参数。

1.2 自动分组多尺度特征融合

为了能自动设计相关参数，提高LCNN 的精确度，笔者在SSCA_MblockNet 中提出了一种自动分组的多尺度特征融合方法（如图2）［28］。在分组多尺度特征提取的基础上，该方法首先利用单目标进化算法对输入特征通道自动分组，然后采用包括1×1 的点卷积、3×3 的标准卷积和3×3 的膨胀卷积在内的3 种尺度的卷积核对自动特征提取通道分组，并融合提取的多尺度特征形成输出特征图。

图2 自动分组多尺度特征融合Fig.2 Automatic grouping multi-scale feature fusion

图2 所示的自动分组的多尺度特征融方法主要改进特征融合模块，包括进化算法自适应分组层、多尺度卷积核特征提取层以及特征融合层。利用该结构对特征图进行特征提取，既可以自动设计特征提取通道分组，避免尺度单一造成的特征提取不充分问题，又可以避免过度使用卷积核提取特征导致的计算量大的问题。

1.3 自动分组多尺度特征融合复杂度分析

本节根据自动分组的多尺度特征融合模块结构中的参数量和计算量来衡量对LCNN 结构的优化程度。

1.3.1 参数量分析

由于考虑的是不同卷积核对应的特征提取通道分组情况对LCNN 特征提取模块参数量和计算量的影响，本文忽略偏置和激活，所有卷积核特征提取元素的数量即为参数量，计算公式为：

其中：L＇为特征融合模块的参数量；Ig为第g组输入特征通道数；CWg为第g组卷积核的宽度；CHg为第g组卷积核的高度；Og为第g组输出特征通道数。

1.3.2 计算量分析

将所有卷积核元素与输入特征图张量对应相乘再相加，相加次数为卷积核元素数减1，相乘次数为卷积核特征提取元素数，则计算量如式（2）所示：

其中：J＇为特征融合模块的计算量；W、H分别为输入特征图的宽度与高度。

1.3.3 结论

由式（1）可知自动分组的多尺度特征融合模块结构参数量的大小主要与卷积核尺寸以及特征通道分组有关。由式（2）可知，当输入输出特征图的高度和宽度以及卷积核的尺寸一定时，各卷积核对应的输入输出特征通道数能够直接影响LCNN 结构的参数量和计算量。引入单目标进化算法对特征通道自适应分组，可以有效优化LCNN 结构的复杂度，但仍存在无法同时兼顾复杂度和精确度的不足。因此，本文提出基于NSGA-Ⅱ的自适应多尺度特征通道分组优化算法，以均衡优化LCNN 的复杂度和精确度。

2 框架及算法

2.1 优化框架

首先，从LCNN 的精确度和复杂度两个方面对基于NSGA-Ⅱ的特征融合层结构优化问题进行双目标函数建模；然后，对多模块自适应分组优化结构的复杂度进行分析，并设计基于NSGA-Ⅱ的LCNN 结构优化框架。

2.1.1 特征融合层结构优化双目标函数建模

将LCNN 的精确度最大化和复杂度最小化作为两个目标，提取LCNN 中不同种类卷积核对应的特征，并将提取出特征的输入和输出通道数作为决策变量x每一维的值，再转化成最小化目标函数问题，确定双目标函数建模公式如下：

其中：F1表示将LCNN 精确度最大化转化为最小化问题求解的目标函数；Ltrue表示分类正确标签数；Lfalse表示分类错误标签数；F2表示LCNN 结构的复杂度；M是特征融合模块数；G为分组卷积操作的组数；xmg、CWm、CHm、Wm、Hm分别表示第m个特征融合模块中，第g组输入输出特征通道数、卷积核的宽度与高度以及特征图的宽度和高度。

2.1.2 多模块自动分组多尺度特征融合结构复杂度分析

与传统LCNN 结构中的特征融合方法相比，基于单目标进化算法的自动多尺度特征通道分组优化方法可以提高LCNN 的精确度。但随着LCNN 结构中自动多尺度特征通道分组优化模块数量的增加，自动分组方案的选择空间也会呈指数增加，这不利于提高LCNN 性能评价的速度，证明如下：

设LCNN 的自动多尺度特征通道分组优化模块数量为A（模块间互不影响），它的输入特征图共有n条通道，根据LCNN 结构的构建要求，每种尺度卷积核对应的特征提取通道数至少为1，那么3 种尺度卷积核对应特征提取通道的不同选择分组情况数，即LCNN 结构优化问题对应的搜索空间的大小如下所示：

由上述分析可以看出，当LCNN 结构中自适应多尺度特征通道分组优化模块数呈线性递增时，不同尺度卷积核对应特征提取通道可选择的分组情况数呈指数型增长。

尽管获得合适的LCNN 特征融合模块的通道分组情况对LCNN 计算效率的提高有正向帮助，但当采用多个自适应多尺度特征通道分组优化模块进一步降低LCNN 复杂度时，LCNN 结构优化问题的搜索空间反倒会增加。而LCNN 结构越复杂，性能评估计算开销也会越大。此外，在降低LCNN参数量和计算量的同时，存在无法根据用户偏好平衡LCNN精确度表现的不足。针对上述问题，将LCNN 结构的复杂度和精确度表现作为两个优化目标，应用快速非支配排序算法对LCNN 作进一步优化，设计LCNN 结构优化框架。

2.1.3 基于NSGA-Ⅱ的LCNN结构优化框架

在多目标进化算法中，NSGA-Ⅱ算法无须分解优化问题，直接根据支配关系比较个体的性能，应用方便，针对双目标优化问题通常能搜索出较好的解决方案。同时，也考虑到建模的优化目标个数不多，因此本文选择NSGA-Ⅱ进行LCNN 结构优化的应用研究。NSGA-Ⅱ算法针对目标函数优化问题需要输入种群规模、问题维度、种群最大评价次数及相关参数设置，输出非支配解集。具体过程包括：

1）初始化。初始化种群并将当前进化代数设置为1。

2）产生子种群，判断是否生成了第一代子种群，若已生成则令进化代数等于2；否则，对初始种群进行非支配排序和选择、高斯交叉、变异，产生第一代子种群并使进化代数等于2。

3）产生合并种群。将父代种群与子代种群合并为新种群。

4）种群演化。判断是否已生成新的父代种群，若未生成则计算新种群中个体的目标函数，并执行快速非支配排序、计算拥挤度、精英策略等操作生成新的父代种群；否则，对生成的父代种群执行选择、高斯交叉、变异操作生成子代种群。

5）判断当前代数是否等于最大的进化代数T，若不大于则进化代数自增1，并返回3）；否则，输出非支配解集，并停止。

利用NSGA-Ⅱ优化LCNN 中的自适应多尺度特征通道分组优化模块，以优化LCNN 结构，平衡LCNN 的精确度和复杂度。通过种群不断进化，搜索出决策空间中性能表现优异的Pareto 最优解集，如图3（a）为目标空间，图3（b）为决策空间（搜索空间）。

图3 基于NSGA-Ⅱ的LCNN结构优化目标及决策空间Fig.3 Structure optimization objective and search space of LCNN based on NSGA-Ⅱ

图3（a）中不同曲线表示目标空间上的非支配前沿，其中黑色实心点虚线为非支配前沿1，为Pareto 最优解集在目标空间中的映射；图3（b）中的各曲线上的点表示决策空间中的解集，其中黑色实心点虚线非支配前沿1 在决策空间中的映射为Pareto 最优解集，即LCNN 结构优化问题的最优解集。由于构建LCNN 中自适应多尺度特征通道分组优化层的关键操作是自适应分组，即需要自动确定式（3）中3 种尺度对应特征通道数xmg。基于NSGA-Ⅱ的自适应分组方法中，需要根据临时LCNN 在临时图像分类数据集上的分类精确度表现确定最终LCNN 特征通道分组结构。因此，需要确定NSGA-Ⅱ演化的相关前提条件、临时LCNN 结构评价方式以及最终LCNN 结构在图像分类数据集上的性能评价指标，如图4 所示。

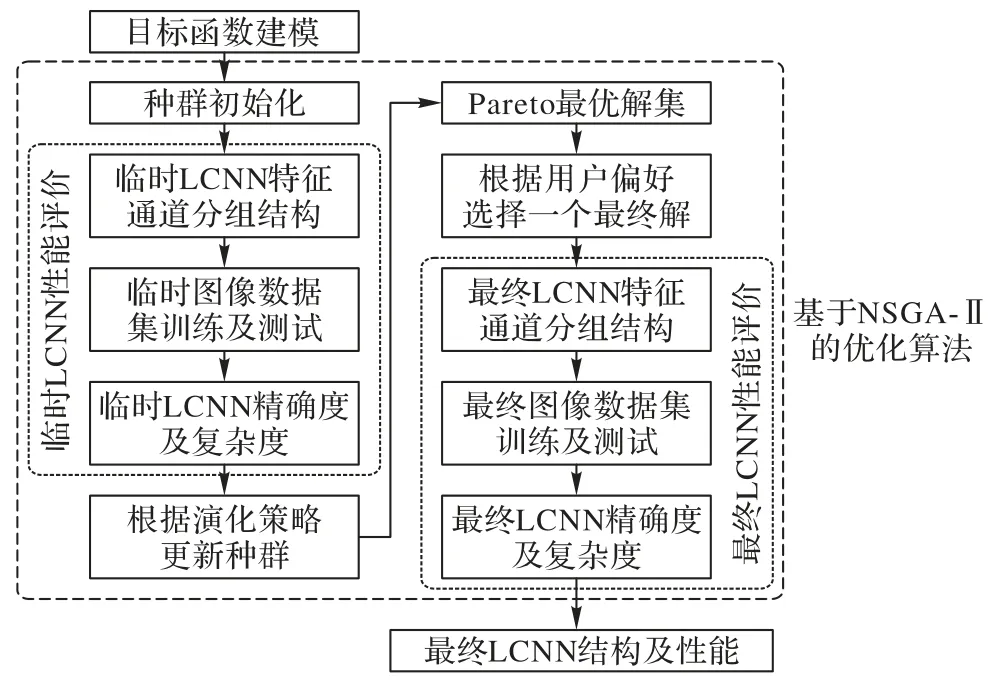
图4 基于NSGA-Ⅱ的LCNN结构优化框架Fig.4 Structure optimization framework of LCNN based on NSGA-Ⅱ

如图4 所示，基于NSGA-Ⅱ的LCNN 结构优化过程包括：

1）根据LCNN（包括临时LCNN 和最终LCNN）在图像分类数据集上的精确度最大化和对应网络结构的复杂度最小化进行目标函数建模，并针对该目标函数优化问题，根据个体编码方式对个体及种群进行初始化，解码初始种群即得到临时LCNN 的特征通道分组结构。

2）将每个个体对应的临时LCNN 结构在从原始图像分类数据集中选择的部分图像分类数据集（选择方式在仿真实验中描述）上进行训练和测试，为了高效估计每个LCNN 结构的潜力，训练和测试次数分别设置为5，运行完毕后获得临时LCNN 分类精确度和复杂度及其对应的特征通道分组结构。

3）根据演化策略更新种群，得到最优解集。设计一组LCNN 特征通道分组结构，然后根据用户偏好选择一个解：若用户更注重网络的精确度表现，即更偏好精确度较大的解时，选择在非支配前沿上的映射更靠近图3（a）目标空间中F2时对应的解；若用户更看中网络的计算效率，即更偏好复杂度较小的解时，选择非支配前沿上的映射更靠近图3（a）目标空间中F1的解。解码选择的解即可获得最终的LCNN特征通道分组结构。

将最终的LCNN 结构在原始图像数据集上进行训练和测试，训练和测试次数分别设置为100，运行结束后得到LCNN 结构及性能评价结果。

2.2 算法设计

2.2.1 NSGA2-AMFCGO算法

基于NSGA-Ⅱ的自适应多尺度特征通道分组优化算法（Adaptive Multi-scale Feature Channel Grouping Optimization algorithm based on NSGA-Ⅱ，NSGA2-AMFCGO）的具体实现如下：

算法1 NSGA2-AMFCGO 算法。

输入 种群初始化的相关参数，种群规模=20，个体维度=8；

输出 非支配解集及其适应度值，即最佳LCNN 结构集合及其对应性能。

1）初始化。初始化种群，并设置当前进化代数t=1。

2）解码初始种群得到临时自适应多尺度特征通道分组模块结构，将其嵌入LCNN 中，构成临时LCNN 结构。

3）根据式（3）建模的双目标函数，对临时LCNN 进行性能评价，得到适应度值。

4）产生子种群。判断是否生成了第一代子种群，若已生成，则设置当前进化代数t=2；否则，根据适应度值对初始种群进行非支配排序和选择、高斯交叉、变异，产生第一代子种群，并设置当前进化代数t=2。

5）循环开始：

5.1）产生合并种群。将父代种群与子代种群合并为新种群。

5.2）种群演化。判断是否已生成新的父代种群：若没有，则根据种群中个体的适应度值，执行快速非支配排序、计算拥挤度、精英策略等操作，生成新的父代种群；否则，对生成的父代种群执行选择、交叉、变异操作生成子代种群。

5.3）判断t是否等于最大的进化代数T，若没有则进化代数自增1，并返回第5）步；否则，从非支配解集中选择一个解，解码得到优化后的自适应多尺度特征通道分组模块结构（设计的结构中包含两个特征提取模块），将其嵌入基于非均匀通道分组多尺度的特征融合LCNN 结构中，得到优化后的LCNN 结构，即基于NSGA-Ⅱ的自适应多尺度的特征融合网络（Adaptive Multi-scale Feature Fusion Network based on NSGA2，NSGA2-AMFFNetwork），并评价该结构性能。

6）停止循环。

算法1 中，个体编码方式为将1×1 点卷积、3×3 标准卷积以及3×3 的膨胀卷积对应的特征提取通道的分组数分别编码到个体的3 个维度上。然后，将种群规模扩充至20。种群规模扩充的具体做法为：a）将设计的第一个自适应多尺度特征通道分组优化模块中3 个待搜索的通道分组数作为个体第1 至3 个维度上的值；同理，将第二个优化模块中的3 个通道分组数作为个体第4 至6 个维度上的值。b）将LCNN 运行得到的图像分类精确度作为个体的精确度，初始值置为0；将LCNN 的复杂度作为个体的复杂度值，其初始值根据式（3）计算。c）个体计数器自增1，并判断个体数是否大于20，若不大于，则返回第3）步；否则，输出初始化后的种群并停止操作。

2.2.2 网络结构

基于NSGA-Ⅱ的自适应多尺度特征通道分组优化模块1（NSGA2-AMFFModule1）包括：深度卷积层和自适应多尺度特征通道分组优化层，如图5 所示，它的输入特征图通道数为96。首先，通过深度卷积层进行特征提取，利用NSGA-Ⅱ在自适应分组层确定3 种尺度的卷积核对应的特征提取通道数分别为g11、g12和g13；然后，进行特征提取，在合并层进行通道合并，最后得到输出特征图。

图5 基于NSGA-Ⅱ的自适应多尺度特征通道分组优化模块1Fig.5 NSGA-Ⅱ based adaptive multi-scale feature fusion module 1

基于NSGA-Ⅱ的自适应多尺度特征通道分组优化模块2（NSGA2-AMFFModule2）包括：在点卷积和深度卷积层特征提取的基础上，利用NSGA-Ⅱ自适应分组特征提取通道，如图6 所示，它的输入特征图通道数为240。首先，依次通过点卷积和深度卷积层进行特征提取；然后利用NSGA-Ⅱ在自适应分组层确定3 种尺度的卷积核对应的特征提取通道数分别为g21、g22和g23；接着，分别进行特征提取及通道合并，得到输出特征图，等待后续处理。

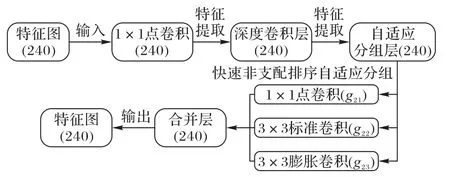
图6 基于NSGA-Ⅱ的自适应多尺度特征通道分组优化模块2Fig.6 NSGA-Ⅱ based adaptive multi-scale feature fusion module 2

将NSGA2-AMFFModule1 嵌入自适应多尺度特征融合层3，NSGA2-AMFFModule2 嵌入自适应多尺度特征融合层7，搭建出NSGA2-AMFFNetwork，如图7 所示。

图7 NSGA2-AMFFNetwork结构Fig.7 Structure of NSGA2-AMFFNetwork

从图7 中可看出，基于NSGA-Ⅱ的自适应多尺度特征通道分组优化LCNN 结构包含10 个卷积层：第1 层为3 × 3 的普通卷积；第2 层为3 × 3 的普通卷积和点卷积组成的深度卷积；第3 层为深度卷积和自适应多尺度特征通道分组优化模块层；第4 至6 层和第8 至10 层均为3 × 3 的普通卷积和点卷积组成的深度卷积；第7 层为点卷积、深度卷积以及自适应多尺度特征通道分组优化模块组成的层。第3 层和第7 层通过基于NSGA-Ⅱ的自适应多尺度特征通道分组优化算法自动搜索最优结构。

3 实验与结果分析

3.1 数据集及运行环境

本实验以图像分类问题为例，采用数据集BloodMNIST。它是Yang 等［29］提出的轻量型医学图像数据集MedMNIST 中基于个体正常细胞的图像，像素大小为28×28，通道数为3。这些图像从没有感染的血液学或肿瘤学方面疾病的人体中采集，在采血时没有任何药物治疗。它总共包含17 092 张图像，分为8 个类。实验中，采用前13 673 张图像作为最终LCNN 的训练集，后3 419 张图像作为最终LCNN 的测试集。为了提高训练速度、降低实验的时间成本，临时LCNN 采用的训练集和测试集的规模是最终LCNN 的1/10，即从原数据集中分别选择前1 367 张和后341 张作为临时LCNN 训练和测试的数据集。临时和最终LCNN 的训练批次大小均设置为128。

硬件环境：实验采用了一台台式机和一台笔记本。台式机的CPU 配置为Intel Core i7，主频3.00 GHz，系统处理器是64 位，8 GB 运行内存；笔记本的CPU 配置为Intel Core i7-8550U，主频1.80 GHz，系统类型是基于x64 的4 核8 线程处理器。

软件环境：实验在Windows 10 系统下进行，使用的机器学习编程框架为谷歌人工智能团队开发和维护的TensorFlow1.14.0。采用Python 语言下的CPU 版本，使用的集成开发环境为PyCharm，使用Python 语言对进化算法和LCNN 结构进行编写和运行。

3.2 复杂度和精确度指标

根据LCNN 结构中的特征融合模块数、特征提取的卷积核尺寸、特征图大小、分组后每组的特征通道数确定LCNN结构的计算量，将其作为衡量LCNN 复杂度的指标，公式为：

其中：Fcomplex表示LCNN 结构的复杂度；M是特征融合模块数；G为分组卷积操作的组数；Img、CWmg、CHmg、Wm、Hm、Omg分别表示第m个特征融合模块中，第g组输入特征通道数、卷积核的宽度与高度、特征图的宽度与高度以及输出特征通道数。

将LCNN 在图像分类任务中的分类正确率作为精确度，即LCNN 的分类正确率为测试正确的标签数与总有效测试标签数的比值：

其中：Ltrue为LCNN 结构在图像分类数据集上的分类正确标签数；Lfalse为LCNN 结构在图像分类数据集上的分类错误标签数。

3.3 数据集实验

构建NSGA2-AMFFNetwork，在BloodMNIST 数据集上与其他经典的LCNN 结构选取10 层网络进行对比。对比结构包括：经典的轻量型卷积神经网络MobileNet_v1［30］、MobileNet_v2［31］、ShuffleNet_v2［32］、DenseNet［33］、基于非均匀分组的轻量型卷积神经网络结构M_blockNet_v1［27］以及基于单目标进化算法的轻量型卷积网络SSCA_MblockNet［28］。它们在BloodMNIST 数据集上运行100 代的平均测试精确度和运行时间对比结果如表1 所示。

表1 平均测试精确度及运行时间对比Tab.1 Comparison of average test accuracy and running time

从表1 中可以看出，NSGA2-AMFFNetwork 的平均测试精确度为92.712 7%，优于对比的其他结构；它的运行时间为4 818 s，在所有对比的LCNN 中排名第4，性能评价消耗的时间较少。对于轻量型卷积神经网络来说，DenseNet 的平均精确度表现比表1 中的其他经典的LCNN 更好。M_blockNet_v1 的平均精确度排名第4，比DenseNet 要低。SSCA_MblockNet 平均精确度排名第2，比优化前的M_blockNet_v1表现更佳，并且超过了DenseNet，但其所需运行时间更长。这是由于SSCA_MblockNet 在建模时只考虑了精确度这个目标，尽管基于单目标进化算法能够自动搜索更合适的LCNN结构，但所需计算代价更大、运行时间更长。NSGA2-AMFFNetwork 与基于单目标进化算法优化的LCNN 结构相比，具有更高的平均精确度和更短的运行时间。这表明，对LCNN 的特征融合层结构优化问题进行双目标函数建模，并利用NSGA-Ⅱ对LCNN 结构进行优化，能够更均衡地优化精确度和搜索效率。实验中的7 种LCNN 结构在图像数据集BloodMNIST 上测试100 次的精确度变化对比如图8 所示。

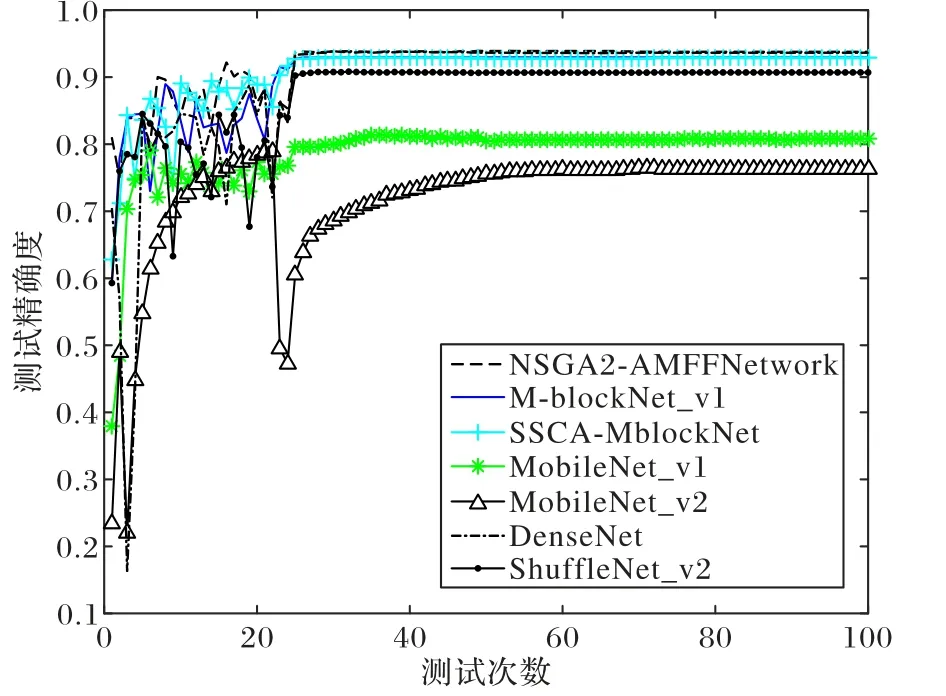
图8 LCNN测试精确度变化对比Fig.8 Comparison of LCNN test accuracy changes

由图8 可以看出，基于NSGA-Ⅱ的自适应多尺度特征通道分组优化算法在测试时具有更稳定的测试精确度和收敛速度。7 种LCNN 结构在图像分类数据集BloodMNIST 上测试25 次左右时均出现跳跃现象，这可能是由于实验中学习率在25 次时发生跳跃变化导致的。本文实验中所有LCNN在训练和测试时学习率统一设置为前25 次取0.01；之后，测试每增加25 次，学习率缩小为原来的1/10。25 次后，所有的LCNN 的精确度表现逐渐趋于收敛。NSGA2-AMFFNetwork得到的一组Pareto 最优解集包含3 组解，如表2 所示。

表2 NSGA2-AMFFNetwork模块的通道分组参数Tab.2 Channel grouping parameters of NSGA2-AMFFNetwork modules

由表2 可知，在数据集上实验，将Pareto 解集解码后，获得NSGA2-AMFFNetwork 两个自适应多尺度特征提取模块的通道分组结构参数。该解集中包含3 个Pareto 非支配解，即3 个临时LCNN 的特征提取通道结构。其中，序号为1 的解，在临时图像分类数据集上测试第5 次时的F1和F2值分别为0.152 673 94 和0.738 235 29；序号为2 的解F1和F2的值分别为0.102 931 15 和0.808 235 29；序号为3 的解F1和F2的值分别为0.104 388 07 和0.798 235 29。本实验中根据用户需要LCNN 精确度与复杂度均适中的偏好（即要求与解集中的其他解相比，被选择的解对应F1和F2的值分别居中），从非支配解集中选择序号为3 的解作为最终解。它被视为满足用户偏好的有潜力的解，将其解码作为最终LCNN 结构。NSGA2-AMFFModule1 的3 种尺度的特征提取通道数分别为80、5、11；NSGA-AMSFFModule2 的3 种尺度的特征提取通道数分别为198、13、29。

设置NSGA-Ⅱ优化前的M_blockNet_v1 特征提取模块的两组参数分别为：64、16、16 以及160、40、40。根据式（1）～（2）分别计算出在BloodMNIST 数据集上优化前后LCNN 结构的参数量和计算量，以及运行100 次的平均测试精确度和运行时间，结果如表3 所示。从表3 可以看出，在BloodMNIST图像分类数据集上，基于NSGA-Ⅱ算法优化后的LCNN 的计算总量比手工设计的LCNN 结构降低了26.505 2×107，平均精确度提升了1.220 2 个百分点，运行时间上降低了41.07%。这说明基于双目标的目标函数建模能在保证LCNN 结构优化程度具有可观竞争力的同时，兼顾LCNN 的精确度性能表现，而且基于NSGA-Ⅱ的优化算法可根据用户偏好和问题需求选择合适的解，对领域知识不足的用户更加友好，针对不同的图像分类问题，更容易找到合适的LCNN结构。

表3 LCNN优化前后复杂度和精确度对比结果Tab.3 Comparison results of complexity and accuracy before and after LCNN optimization

3.4 特征图

为了验证基于NSGA-Ⅱ的自适应多尺度特征通道分组优化算法对卷积模块和最终网络的优化效果，选取原始医学图像分类数据集BloodMNIST 中大小为28×28×3 的8 张人体细胞图进行展示，如图9 所示。

图10 展示了原始图像在经过NSGA2-AMFFNetwork 中的深度卷积层2 卷积后的特征图结果，以及NSGA2-AMFFModule1 优化前后的特征图结果。在基于NSGA-Ⅱ的LCNN 结构中，对种群进行初始化、训练和测试、根据演化策略更新种群得到最优解集，可以看作是对网络优化前的操作，它对应的特征图结果主要表现为两个模块特征图的不同。从图10 还可以看出，优化后模块1 的特征图结果所含的图像信息更加丰富，从而使分类结果更加准确。这是由于采用算法优化后的模块1 中算法优化后选择的点卷积特征通道数更多，可以使特征提取信息更细致。模块1 中，算法优化后选择的标准卷积和膨胀卷积通道数更少，这可以使当前特征图保留更多的信息，方便后续特征提取。

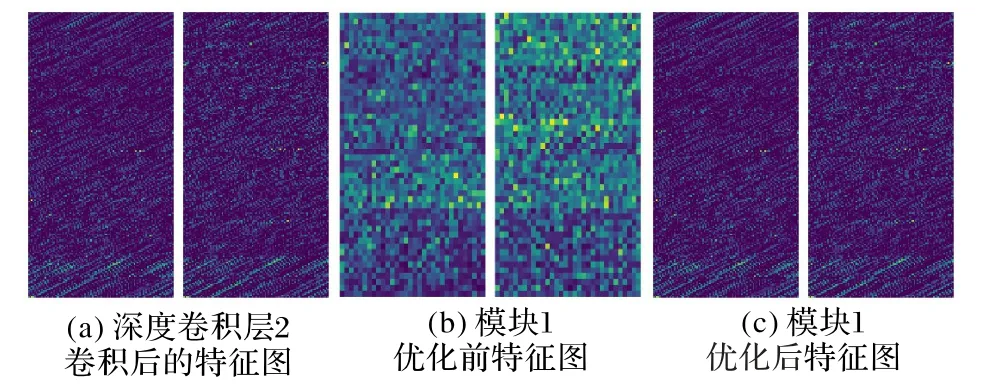
图10 深度卷积层2及NSGA2-AMFFModule1优化前后特征图Fig.10 Feature maps of deep convolution layer 2 and NSGA2-AMSFFModule1 before and after optimization

深度卷积层6 特征提取以及NSGA2-AMFFModule2 优化前后的特征图结果如图11 所示。比较图10 和图11 可以看出，经过种群演化选择后的不同尺度对应的特征通道分组设置，使特征图所含信息比优化前更加丰富。

图11 深度卷积层6及NSGA2-AMFFMoudle2优化前后特征图Fig.11 Feature maps of deep convolution layer 6 and NSGA2-AMSFFMoudle2 before and after optimization

经过深度卷积层10 特征提取后的特征图结果，即NSGA2-AMSFFNetwork 结构优化前后对应的特征图结果如图12 所示。

图12 NSGA2-AMSFFNetwork优化前后特征图Fig.12 Feature maps of NSGA2-AMSFFNetwork before and after optimization

由图10～12 所示的特征图可知，在基于NSGA-Ⅱ的LCNN 中，两个模块中3 种尺度的卷积核对应的特征通道分组优化后，能提取更加丰富的特征信息，从而提高分类结果的准确度，进而说明提出的基于NSGA-Ⅱ的LCNN 特征通道分组结构优化算法是有效的。

4 结语

本文针对LCNN 结构的复杂度和精确度优化不平衡问题，提出了基于NSGA-Ⅱ的自适应多尺度特征通道分组优化算法。首先，针对特征通道分组优化问题进行双目标函数建模，设计基于NSGA-Ⅱ的LCNN 特征通道分组结构优化框架及算法；然后，构建基于NSGA-Ⅱ的自适应多尺度特征通道分组优化LCNN 结构；最后，在图像分类数据集上进行对比实验。实验结果表明，基于NSGA-Ⅱ的自适应多尺度特征通道分组优化LCNN 特征通道分组结构在平衡精确度和复杂度方面具有竞争力。

多目标进化算法NSGA-Ⅱ对LCNN 结构优化易陷入局部最优，可以进一步研究对LCNN 结构的全局搜索和优化。此外，可将降低性能评价时间作为另一个目标，进行三目标函数建模，从而提高网络性能。