基于小波变换CNN 的电机运行状态识别研究

龙 慧，马家庆，吴钦木，何志琴，陈昌盛，覃 涛

（贵州大学 电气工程学院，贵阳 550025）

0 引言

电机作为重要的机械设备，在生产和生活中被广泛应用，电机在运行过程中一般会伴随着温升的产生，发生故障，从而影响到设备的正常运行。为了保障设备的安全运行，及时对电机进行故障识别是一项很重要的技术［1］。随着计算机技术的快速发展，卷积神经网络（Convolution Neural Network，CNN）被广泛应用于电机的故障识别。

CNN 在数据图像特征提取方面有着显著的优势，目前已经被广泛应用于图像识别、人脸识别、特征分类等方面。特征提取是CNN 模型对电机运行状态识别的关键部分，已经被广泛研究。小波变换（Discrete Wavelet Transform，DWT）有非冗余性，能很好的对数据进行分解与去噪，并能将信号中的时频特征表现出来［2］。DWT 在图像降噪处理领域被广泛应用，文献［3］先利用离散傅里叶变换，将时域信息特征映射到频域，再使用CNN 学习数据特征，从而实现故障诊断；文献［4］提出一种基于CNN 和离散小波变换的滚动轴承故障诊断方法，对不同情况下的滚动轴承进行故障诊断；文献［5］结合DWT、Lorenz 混沌系统和CNN 对电力电缆的绝缘故障进行识别；文献［6］提出了一种基于小波时频图和卷积神经网络的断路器故障诊断方法，实现对操动机构故障状态的辨识诊断；文献［7］利用DWT 从原始信号中提取高维器具特征，提出了主动深度学习对负载进行识别的方法；文献［8］提出了一种CNN 的状态监测特征学习模型，对图像数据进行分类。

本文基于小波变换（Discrete Wavelet Transform，DWT）的改进卷积神经网络（Improved Convolutional Neural Network，ICNN）电机运行状态识别方法，将小波变换和卷积神经网络相结合，解决电机故障识别的问题。该方法先构建电机运行状态的数据集，小波变换将采集的数据图像转换为小波系数矩阵并进行系数增强，将处理后的图像输入到网络模型中，对变换后的图像进行特征提取，来提高电机运行状态识别的准确率。

1 理论基础

1.1 小波变换

小波变换是由傅里叶变换发展而来的，小波变换对于复杂信号有着较好的时频分辨率，被广泛应用于复杂单尺度信号的时频分析，通过不同的变换方法从不同的角度获得信号的特征，从而来实现信号的分析和处理。小波变换是一种以时频为特征的时频分析技术，是对不同分辨率信号进行分析的方法。

小波变换分为连续小波变换和离散小波变换。小波变换常用来抑制信号的噪声，本文采用离散小波变换来对数据图像信号进行小波系数变换。

离散小波函数ψm，k（t）可以表示为式（1）：

其中，m和k分别为伸缩和平移参数；t是时间；ψ（t）是小波基。

输入信号由低频（LF）和高频（HF）组成，通过DWT 将其分解成频带，通过下采样得到第一级小波变换。

根据离散小波的特点，低频系数cAi和高频系数cDi的频带分别表示为式（2）和式（3）：

其中，i为分解层数，fs为信号的采样频率。

由于信号已被下采样，因此在重新配置时需要对其进行上采样。小波变换是一种有效的定时信号压缩降噪方法，具有多分辨率和时频局部化等特点。

1.2 卷积神经网络

本文的网络模型由输入层、卷积层、池化层、全连接层和输出层所组成。卷积层是将输入层接收到经过DWT 预处理的特征利用卷积核对数据特征进行提取，增强原始图像的特征信息。卷积操作的一般形式为式（4）：

其中，∗为卷积运算符；b为偏差；ωij为卷积核；x为输入特征图；f（·）为激活函数。

池化层采用平均池化操作将卷积层提取的特征再次提取，使得其有更低的维度，减少计算量和过拟合的产生。池化层的一般形式为式（5）：

其中，β为偏置系数，down（·）为下采样函数。

选用Tanh 激活函数，其取值范围为-1～1，输出均值是0，Tanh 函数表示为式（6）：

全连接层的特征是每一个神经元都与上一层的所有神经元相连。全连接层的输出为式（7）：

其中，x为全连接层的输入，ω为权值系数。

输出层一般是分类器层（Softmax 层），对识别目标进行分类。Softmax 层的输入是上一层全连接层的数据，输出的数据的每个值范围为0～1，输出值表示的是样本属于这一类别的概率。

2 基于DWT 的CNN 的电机运行状态识别方法

对于本文基于DWT 的ICNN 电机运行状态识别方法，将电机原始数据通过小波变换转化为小波系数矩阵，再通过ICNN 进行无监督的学习时频图的图像特征，识别出电机故障的特征信息，最后由Softmax 分类层将识别出的特征信息与相应故障类型做出对比，实现了电机的运行状态识别诊断。

基于DWT 的CNN 的电机运行状态识别的具体步骤：

（1）通过热像仪采集电机图像数据集，将数据集预处理后划分为训练集和测试集；

（2）将数据集通过DWT 处理数据图像，对数据图像进行小波系数矩阵的转换；

（3）将处理后的数据图像输入到CNN 模型中，初始化网络模型，根据实验需求，确定适合本实验模型的学习率和迭代次数等网络参数；

（4）通过网络模型运行得到输出误差，判断输出是否收敛；若不收敛执行步骤（5），若收敛直接进行识别；

（5）通过模型输出的误差进行反向传播，进行权值的修改；

（6）重复执行步骤（4）、步骤（5），直到模型的精度和损失函数等满足实验要求，输出网络模型，识别电机的运行状态。

3 实验结果分析

3.1 数据集

实验平台主要由电力电子技术及电机控制实验装置、电机、热像仪和计算机组成。通过热像仪采集电机运行状态的图像，将采集到的电机数据分为正常运行、停止和故障3 种状态，每种状态采集200 个样本，从总样本中随机选取20%构成测试样本，剩余的数据作为训练样本。对这3 种状态的图像预处理，然后进行离散小波变换得系数矩阵，再输入到CNN 网络模型。

3.2 评价指标

3.2.1 损失函数（Loss）

用损失函数评估模型的预测值与真实值之间的不一致程度，式（8）：

其中，p（x）为真实的概率，q（x）为模型通过计算之后的概率估计。

3.2.2 结构相似函数（SSIM）

结构相似函数用于评估模型运算后电机识别图片的失真程度，识别前后两张图像的结构相似函数SIMM，如式（9）：

其中，μ为平均像素值；σ为标准差；C为常数。

3.3 实验分析

迭代50 次、权值调整步进值为0.03 时所得到的实验结果见表1。通过对不同小波变换（Haar 小波、Daubechies（db）小波、ReverseBior（rbio）小波、Coiflet（Coif）小波和Fejer-Korovkin（fk）小波）的故障识别的性能比较，可以看出本文使用的小波变换表现出最好的性能。

表1 不同小波变换在迭代50 次下运行状态识别的性能比较Tab.1 Performance comparison of different wavelet transforms in running state recognition under 50 iterations

权值调整为0.03 时数据图像在不同迭代次数下的结果如图1 所示，可以看出随着迭代次数的增加，准确率逐渐升高、损失值逐渐减小；当迭代次数大于40 时，迭代次数的增加，准确率和损失函数几乎都趋于稳定，准确率在97%及以上，损失函数的值在0.2 附近波动。但随着迭代次数的增加，模型运行所需要的时间也在不断增加，为了节省时间且保证有好的准确率和损失值，本文所选择的迭代次数为50，模型不仅能达到实验所需的实验精度，而且收敛速度比较快，稳定性较好。

图1 数据图像在不同迭代次数下的比较Fig.1 Comparison of data images under different iterations

为了进一步验证本文所提方法的稳定性和可行性，在不同权值调整下对电机进行故障识别，结果如图2 所示。可以看出，权值过大或过小都会使准确率相对过低、损失函数值过大；当权值调整为0.05时，本文所提出的方法的损失值和准确率都达到很好的效果，达到98%。

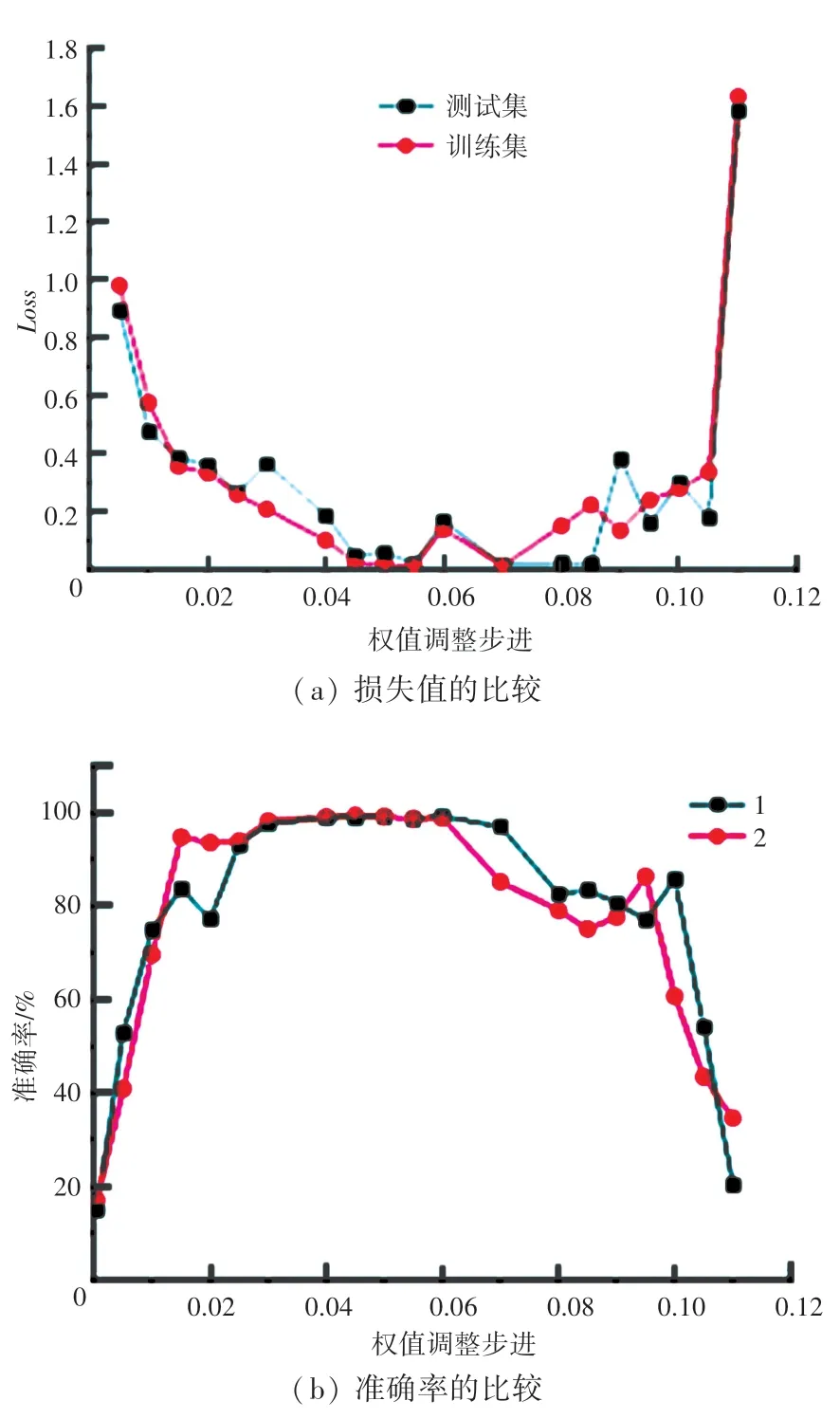
图2 数据图像在不同权值下的比较Fig.2 Comparison of data images under different weight adjustment

4 结束语

本文基于DWT 的CNN 实现了电机运行状态识别。该方法将小波变换和卷积神经网络结合在一起，很好的避免了传统方法对于经验的依赖，利用DWT 小波系数的特点，对数据图像进行转换，提取数据的重要特征，提高了电机运行状态识别的准确率。实验结果表明，迭代次数不断增加，准确率不断增大，最后趋于一个稳定状态，准确率达到最高的时候，损失函数值也达到最低，说明该方法有效。