基于q-高斯过程下的带红利欧式期权定价
刘利敏,闫钰蕾
(河南师范大学 数学与信息科学学院,河南 新乡 453007)
在金融市场的发展进程中,期权既具有套期保值、规避风险等作用,又具有灵活性和多变性等特点,所以成为金融市场上最具潜力的金融衍生产品.1973年,BLACK等[1]导出了著名的Black-Scholes期权定价公式,MERTON[2]在B-S模型的基础上引入Poisson跳过程来刻画股票价格过程存在跳跃的情况,并考虑了股票以红利率形式支付分红的情况,导出了支付分红的欧式期权定价公式,从而将分红问题引入期权定价理论研究中.1975年,BLACK[3]又提出了离散分红的情形,并指出标的股票的初始价格是其实际价格减去分红现值.基于无套利条件,2002年,CHANCE[4]考虑了股票离散分红的欧式期权定价问题,并假设存在标的资产为股票未来分红的分红远期合约,从而构建投资组合.然而,只有在有分红的情况下,这种分红远期合同才有意义,使得该研究方法具有局限性.基于CHANCE[4]的结论,MATOS等[5]改进了其投资组合策略构造了新的套期保值策略,该策略包括基本资产、无风险零息债券和股息条.由于市场上不会存在偶然构建的分红远期合约,所以,Matos的策略更为合理.
经典的期权定价研究中股票的价格都是布朗运动驱动的,无法刻画价格的长相依性,因此很多学者改进了价格模型.文献[6-8]都用分数布朗运动代替布朗运动刻画长记忆性;文献[9-12]用q-高斯过程代替布朗运动刻画长记忆性.
1 基于q-高斯过程的带红利欧式期权定价
假设市场中有两类资产,一类是无风险资产,如无风险债券,t时刻的价格为Bt,满足dBt=rBtdt.另一类是风险资产,假设为股票,t时刻的股票价格为St,满足
dSt=μStdt+σStdΩ(t).
(1)
其中Ω(t)遵循以下随机过程
(2)
其中r为无风险利率,Wt为零均值高斯白噪声,当q=1时,为标准布朗运动.P(Ω(t),t)的形式如下,

引理1[11]股票价格由q-高斯过程驱动的欧式看涨期权定价公式为
Ct=StMq(γ1,γ2)-Ke-r(T-t)Nq(γ1,γ2).
(3)
其中
(4)
理论上的分红方式有两种:一种是连续分红,即每年按一定比例将股票或其他资产获得的利润支付给投资者,这个比例称为红利率,在本文用α表示;另一种分红方式是离散分红,可以是固定时刻固定分红的分红方式,也可以是离散随机分红,离散随机分红又分为分红值随机,或者随机时刻产生固定分红.
1.1 连续红利的期权定价
定理1令红利率为α,标的资产为持续分红的股票,当敲定价格为K,到期日为T时的欧式看涨期权的价格为
Ct=e-α(T-t)StMq(γ1,γ2)-Ke-r(T-t)Nq(γ1,γ2).
(5)
这里Mq(γ1,γ2)和Nq(γ1,γ2)由式(4)给出.
证明为了得到连续分红的期权定价,首先考虑一个不带分红情况的投资组合,假设h1是在t时对股票S的投资额,h2是在t时对期权C的投资额.然后,投资组合的总资产Q在时间t满足
Q=h1+h2.
(6)
在时间t+dt,投资组合的回报是
(7)
这里dSt/St和dCt/Ct分别代表股票和期权在[t,t+dt]时间段内的收益.根据It公式
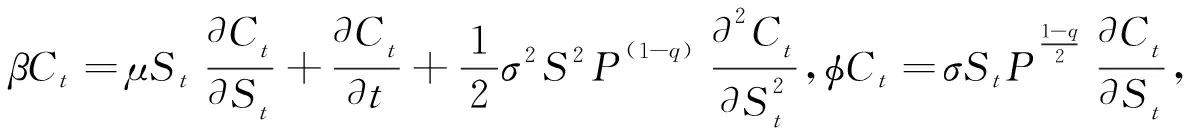
dCt=βCtdt+φCtdWt.
(8)
由式(1)、(2)和(8)有
(9)
适当的h1和h2使投资组合无风险,因此式(9)中dWt之前的系数应为0,即
(10)
(11)
令g1=h1/(h1+h2),g2=h2/(h1+h2),则
g1+g2=1.
(12)
通过分别替换β和φ的值,得到期权价格Ct满足
(13)
式(13)即为股票价格由q-高斯过程驱动的Black-Scholes微分方程.
Ct=StMq(γ1,γ2)-Ke-r(T-t)Nq(γ1,γ2).
为微分方程(13)的解,其中参数值由式(4)给出.
下面给出在q-高斯过程下带红利率的欧式看涨期权的定价公式.根据式(10)和(11),有
(14)
设Dt为单位时间的分红,在式(1)中μ为预期收益率,则分红后的预期收益率为μ-Dt/St,假设分红后的期权价格函数为C(St,t),根据It公式可得
由β和φ的定义,有
(15)
通过应用式(14)和(15),可以得到期权定价的带红利的随机微分方程
(16)
MERTON[2]在带分红的股票价格由布朗运动驱动情况下的随机微分方程为
(17)
当Dt=αSt时,所得到的在布朗运动下具有连续红利率α的期权定价公式为
W=e-αTSN(d1)-Ke-rTN(d2).
根据文献[2]得到的带分红的期权定价公式,结合式(3)类比推导出方程(16)的解为
Ct=e-αTStMq(γ1,γ2)-Ke-r(T-t)Nq(γ1,γ2).
1.2 离散分红的期权定价
由于采用连续红利率的形式进行分红属于较为理想的分红方式,所以大部分股票采用的都是在固定时间进行离散分红.假设在时刻τ进行分红.如果τ>T,则在周期[0,T]之内不存在分红,所以如果想要获得分红则需τ C=(St-Dt(τ))N(d1)-Ke-r(T-t)N(d2). 根据上式,可以推及股票价格由q-高斯过程驱动的带离散分红的欧式看涨期权定价公式. 定理2行权价格为K,到期日为T,带离散分红的欧式看涨期权在τ时间的价格为 Ct=(St-Dt(τ))Mq(γ1,γ2)-Ke-r(T-t)Nq(γ1,γ2). (18) 文献[5]改进了文献[4]的投资组合策略,但是结果没有改变.并且文献[5]构建的投资组合已被证明是连续的,自融资的,而且可以复制到期时看涨期权的价值.所以采用与文献[5]相同的投资策略,即可得到q-高斯过程下具有离散分红的期权定价公式(18),在此不做过多阐述. 将式(2)代入式(1)可得: (19) 式(19)中含有3个待估参数,分别为μ,σ,q.由于同时对3个参数进行估计比较困难,所以将其分开来估计. 最后是波动率σ.根据伊藤公式, 将区间[0,T]进行划分,令0=t0 (20) 由于在实际中采用连续红利率分红的情况较少,所以本节不对连续红利率的分红方式进行模拟.只对离散分红的进行模拟验证.首先分析固定时间固定分红值的期权价格情况.令股票的初始价格为S0=50,无风险利率为r=0.05,敲定价格K=45,q=1.3,T=1,σ=0.2.在计算期权价格理论值之前,需要计算出Mq(γ1,γ2),Nq(γ1,γ2).借助文献[11]的方法,对式(4)中出现的参数d1(q),d2(q),d3(q),d4(q)利用用最小二乘法对其进行估计.通过计算得到当q=1.3时,d1(q)=0.169 2,d2(q)=0.008 0,d3(q)=0.049 8,d4(q)=0.742 2. 分别生成100,1 000,1 500,2 000条股票价格路径,得到对应的模拟期权值,和由式(18)得到的理论值进行比较分析.表1给出了在第5个和第6个时间节点处分别进行D=1以及D=2分红的期权价格. 表1 分红时刻不同以及分红值不同对应的期权价格 随着模拟路径条数的增多,理论值与模拟值之间的误差越来越小,理论值越来越接近模拟值,这反映了所得到的期权定价公式(18)是合理有效的.此外,还可以发现分红时刻的不同以及分红值的大小都会影响期权价格,随着分红时刻的推迟,所对应的期权价格呈上升趋势,且当分红时刻不变时,固定分红值越小,期权价格越高,这些情况都与实际的市场规律相符合. 下面研究当分红时刻是随机时,期权价格的变化情况.假设在随机时间τ产生离散固定分红D.当τ-t 选择不同的λ各生成100个随机数,代表每个股价路径的分红时间.由于到期日T=1,所以如果发现τ大于1时,就意味着在这条路径上不存在分红.通过对随机数的观察可以发现,当λ=0.3时,有3个值大于1;当λ=0.4时,有8个值大于1;当λ=0.8时,有38个值大于1.随着λ的增加,不分红股票的价格路径逐渐增多. 下面比较当λ不同时,期权价格理论值与模拟价格之间的误差. 从表2可以看出,λ不同时,理论值与模拟值之间的误差都较小,表明虽然分红时刻随机,但根据期权定价公式算得的期权价格仍是合理的.并且发现随着λ的增加,不分红股票价格路径逐渐增多,期权价格也随之升高,因为在市场中标的资产产生的红利将降低标的资产的价格,这也说明了公式(18)是符合实际的. 令S0=50,T=1,q=1.3,μ=0.1,σ=0.2通过蒙特卡罗数值模拟生成1条股票价格路径,假设路径上有100个节点,每个节点代表一个股票价格.令初始设定值为H=0.588 2,q=1.3,μ=0.1,σ=0.2,利用第1部分的方法模拟得到对应的参数估计值分别为H=0.583 1,q=1.285 0,μ=0.099 2,σ=0.225 6.与设定值之间的误差为ΔH=0.005 1,Δq=0.015 0,Δμ=0.000 8,Δσ=0.025 6,通过对数据的观察可以发现模拟值与设定的参数值之间误差效果较好. 下面验证所得估计量的稳定性,分别生成并选取100条,500条,1 000条股票价格序列来对参数进行估计,得到的估计值由这些路径模拟出来的数值的均值E来代替.并通过计算方差V进一步观察估计量稳定的效果.模拟结果见表3. 表2 λ不同时对应的期权价格 表3 估计量的稳定性模拟 由表3可知q值的大小对参数μ,σ估计量的大小没有产生大的波动,其中μ的估计值仍在0.1附近,σ的估计值仍在0.2附近,可见q的改变对其他两个参数的估计值以及估计效果并没有产生特别大的影响.随着路径条数的增加,估计量模拟值与设定值之间的误差都越来越小,这说明估计值在设定值周围的上下波动幅度越来越小,越来越趋于设定的参数值,并且在表3中可以看到各组方差的数值也较小,这都证明了估计量的稳定性,也反映出第2部分提出的估计方法较为合理. 将8月9日看作期权起始日,将那天的股票价格作为初始价格S0,即S0=288.33,无风险利率r取美国一年期国债利率r=1.09%.MSFT股票的连续红利率不是固定不变的,在不同的时期有不同的红利率.在8月9日至9月24日这期间连续红利率为α=0.75%,随后将各参数值代入式(13)得到理论期权值.对于固定分红,通过搜索数据可知2021年11月17日进行一次Dτ=0.62的分红,根据Dt(τ)=E[Dτe-r(τ-t)|Ft]可知贴现到9月24日则有Dt(τ)=0.572 2,将Dt(τ)与各个参数值代入式(17)得到理论期权值. 通过对表4的分析可知,无论是带连续红利率的分红还是在固定时刻的离散分红,这两种分红方式所得到的理论值也都随着敲定价格K的增大而减小,并且与真实值都较为接近,理论值与真实值之间误差较小,这说明理论值符合实际市场情况,也反映了得到的带分红的期权定价公式合理有效. 表4 带红利率和固定分红的不同敲定价K对应的期权值2 q-高斯过程的参数估计
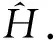

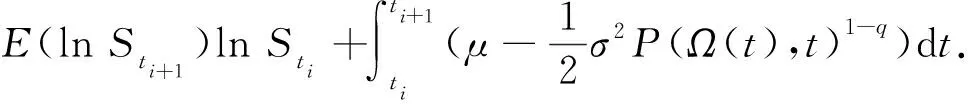

2.1 期权定价的数值模拟

2.2 参数估计的模拟研究


3 实证分析