低阶长焰煤细观结构定量分析与表征单元确定
丁自伟 ,高成登 ,王耀声 ,李 亮 ,唐青豹 ,贾金兑 ,李小菲 ,王少懿
(1.西安科技大学 能源学院, 陕西 西安 710054;2.西部矿井开采及灾害防治教育部重点实验室, 陕西 西安 710054;3.陕西煤业化工技术研究院有限责任公司, 陕西 西安 710100)
0 引 言
煤体由于其组成的多样性、长期地质构造及开采扰动作用而呈现强烈的介质非均匀性和结构非连续性[1],其内部的孔隙、裂隙等微细观结构对煤体的物理力学性质与灾变行为有重要的影响和显著的尺度效应,煤体失稳致灾是孔隙裂隙快速起裂非稳定性扩展的集中表现[2]。煤体内部微细观复杂结构定量表征结果的跨尺度整合是构建考虑细观结构信息的宏观本构模型、强度准则和失效判据的基础[3]。如何整合多尺度孔隙微裂隙表征结果成为实现煤体细观结构与宏观性质相关联的热点与难点,表征单元体(Representative Elementary Volume,REV)作为量化尺度效应的一种基本方法,当煤体尺寸大于REV 尺度时,其物理力学特性参数趋于稳定,REV尺度下的煤体特性有效代表了整个煤体的特性。因此,基于定量化的孔裂隙结构信息研究确定合理尺寸的煤体细观结构REV 单元成为煤体宏细观跨尺度研究的关键。
现代微细观成像及图像处理技术因其能够精准识别并数字表达材料细观尺度的空间结构和形态特征,被广泛应用于煤体细观损伤力学研究中[4]。孙传猛等[5]基于引入图像增强算子和规范初始水平集函数的LBF 改进模型能有效处理灰度不均的煤岩图像,实现了对煤岩细观结构的定量描述。宫伟力等[6]应用小波多尺度变换、图像分割以及图像重建技术对煤样SEM 图像进行多分辨率分析。笔者等[7-9]利用类间方差全阈值(Otsu)分割法定量表征煤岩细观结构,进行煤岩识别、关键裂纹确定并建立细观分形特征与强度的力学关系。曹树刚等[10]提出一种基于图像增强函数的改进C-V 模型对含单一和多裂隙煤岩细观图像能有效的分割和识别。邹俊鹏等[11]通过对比煤样最高灰度值像素占比主观选取合适阈值对垂直层理和平行层理低阶煤SEM 图像二值分割,研究其微观形态及微裂隙发育的各向异性特征。由此可见,上述数字图像处理中最重要的是对图像进行精准二值化分割,由于煤体赋存条件的复杂性和组成成分的多样性,针对不同的煤样寻求一种简单有效的图像处理技术进行定量提取和分析对煤体宏细观尺度效应的研究显得尤为重要。
目前,已有大量基于煤岩体细观结构的REV 研究。LONG 等[12]、ODA[13]将Bear[14]首先提出的REV 概念引入裂隙岩体研究领域。刘语等[15]以粉细砂岩孔隙结构8 个参数(孔隙率、孔隙数量、孔隙平均体积、最小体积、最大半径、最小半径、平均直径、平均形状因子)的最大REV 尺寸(400 像素)为岩样细观结构统一REV 边长。程志林等[16]通过岩石孔隙率及图像自相关函数确定二维图像REV 大小为300~500 pix 范围内。卢波等[17]应用分形维数描述岩体结构特征的尺度效应并作为REV 判定参数。WU 等[18]利用计盒维数计算煤体CT 图像二维、三维分形尺寸与孔隙率的关系,并确定了不同煤样的REV 大小(290、160 和120 像素)。在煤岩细观结构REV 研究中,其特征参数包括孔隙率、分形维数、形状因子、孔隙体积、孔隙半径、孔隙直径等,由于所选参数的不同确定的REV 尺寸差异较大,且REV 单元取样方法及选取参数是否能准确描述煤岩体内部非连续性结构的几何特性缺乏定量的分析。因此,有必要考虑煤体细观结构非均质性和各向异性对REV 单元取样的影响,并综合确定具有代表性的特征参数,以确定有效的REV 尺寸。
以彬长矿区孟村煤矿9 组低阶长焰煤试样为研究对象,对煤样依次进行单轴压缩、扫描电镜以及数字图像处理试验,基于煤样孔裂隙结构准确识别与几何特性定量分析,选择并给出了REV 确定的代表性参数,在考虑非均质性和各向异性REV 单元取样方法的前提下,确定了煤体细观结构REV 尺度。
1 煤样与试验
1.1 试样及试验方法
试验的煤样取自陕西彬长孟村煤矿低阶长焰煤,该煤具有中高挥发分、特低水低硫、特高热值且质硬而脆等特点[19]。含碳量高达80%以上,燃烧时火焰长而多烟且不结焦,是主要的动力燃烧和化工用煤。根据国标GB482-2008《煤层煤岩采取方法》共采集9 个煤样,制成(直径D×高度H=50 mm×100 mm)国际标准试件(ISRM),按照采样深度煤样标号为M1~M9,其中通过单轴压缩试验及扫描电镜得到单轴抗压强度和SEM 灰度图片,试验结果见表1。

表1 煤样单轴抗压强度及扫描电镜测试结果汇总Table 1 Summary of uniaxial compressive strength and scanning electron microscope test results of coal samples
采用JSM-6460LV 型扫描电镜进行煤样细观形貌及结构观察并获取扫描图像,放大倍数可达300 000 倍,能谱能量分辨率为129.45 eV。试验时,为保持煤样品原始的表面形态及结构,选取标准试件压缩后大小为(5±2)mm 块状煤样进行扫描观测,更接近于煤样多孔结构的真实状态。采用背散射电子成像技术,在加速电压30 kV,工作距离5 mm,低真空模式4.0 nm 条件下,对试样进行不同倍率的连续扫描,分别得到放大×200、×500、×1 000、×2 000、×5 000 倍的煤样表面微区形貌特征图像。
1.2 煤样图像灰度
通过对比发现,2 000 倍放大倍数下煤样SEM图像骨架结构更为清晰全面,因而取放大2 000 倍的煤样图像进行灰度特性分析(以M1 和M2 为例)。在图像纵向上截取a—a、b—b、c—c、d—d线段提取对应的灰度值,如图1 所示,可以清晰地看出图像灰度值的变化情况。图1 中4 条线从左到右随着图像景深的不同其灰度值起伏变化剧烈,由图像中红色d—d测线分析可得:灰度值曲线呈现多个尖锐的波峰和波谷,且波峰与波谷间的斜率基本一致,当处于高密度煤样基质时,灰度值处于波峰阶段,当处于孔裂隙区域时,灰度值处于波谷阶段。由图像灰度值曲线分析可知,煤样微细观结构灰度值曲线犬牙交错,其灰度表现出严重的不均一性。通过Surface Plot 拾取图像灰度值进行煤样基质与孔裂隙结构表面三维可视化,其结构形态得以更加直接地呈现,由图1 右侧三维曲面图可知,孔裂隙分布具有一定的层理性,但煤体表面结构复杂,边界信息相对模糊。
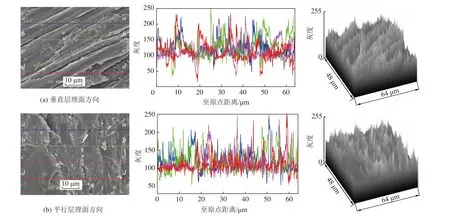
图1 煤样灰度分布曲线及三维曲面图Fig.1 Gray distribution curve and 3D surface map of coal sample
2 煤样细观结构定量表征
2.1 细观结构图像处理
煤样孔隙结构表征的核心是进行有效的阈值分割与孔隙边界分离,实现准确区分孔裂隙和煤样基质。利用Fiji 对煤样SEM 进行图像处理、信息提取,实现图像可视化。
基于煤体细观结构特征提出了一种孔裂隙结构快速识别与定量分析的图像处理方法,基本流程包括:首先对煤样灰度图像进行批量预处理,减少图像灰度差异、图像噪声及对比度偏低对孔裂隙识别的影响;其次进行图像最佳阈值二值化分割,实现煤样孔裂隙结构准确识别,最后,对二值图像进行形态学处理,消除煤屑碎粒杂质及图像单点像素的影响。煤样SEM 图像处理流程如图2 所示。
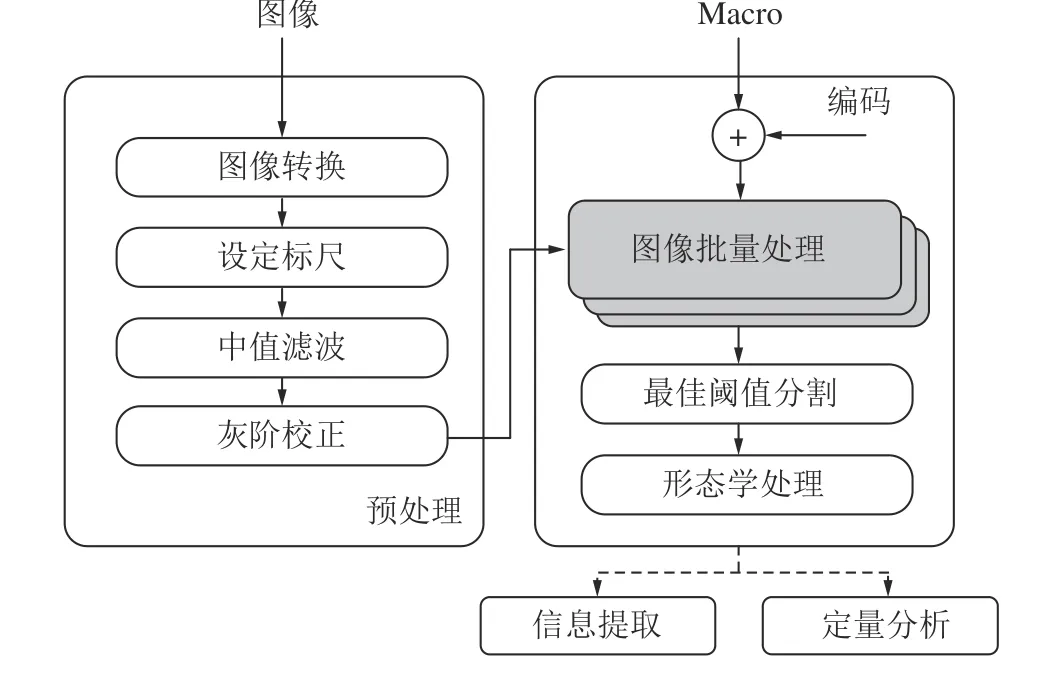
图2 煤样SEM 图像处理流程Fig.2 Coal sample SEM image processing flow
2.1.1 图像预处理
通过图像灰度分析发现,煤样SEM 图像存在灰度不均、对比度偏低、孔裂隙边缘信息模糊等缺点。因此,在图像阈值分割前需要进行图像预处理。
如图2 所示,首先将扫描电镜图像转为8bit 灰度图像,并进行标尺校对,将像素单位转换为长度单位。SEM 图像大小为1 280 pix×960 pix,在放大2 000倍时,一个像素单位代表物理尺寸为0.05 μm,则图像实际尺寸为64 μm×48 μm。其次,为减少图像中的噪声影响,采用中值滤波对图像进行历遍处理。相较于其它滤波技术,中值滤波能有效消除斑点、椒盐噪声,提高信噪比增加图像清晰度,同时可以很好地保留图像孔裂隙边缘信息。最后,对灰度不均的图像进行灰阶校正,减少扫描中产生的灰度差异。通过图像灰度直方图均衡化使灰度均匀分布从而增大图像局部对比度,突出图像特征。上述图像处理过程可通过Fiji 内置的Macro 记录生成代码文件,在需要进行同样步骤的图像处理时,可实现图像批量处理,减少重复性操作以提高图像处理效率。
2.1.2 图像二值化
数字图像是由像素组成的二维矩阵,按行与列分割成m×n个网格,即用一个m×n的像素矩阵来表达图像元素,通过预处理后的灰度图像包含256 个灰阶,选择合适的灰度阈值可以将图像中像素矩阵的灰度值划分为只含0 和255 的黑白位图,从而使扫描电镜图像转换为只包含孔裂隙和煤基质的二值图像。
式中:f(x,y)为原始图像像素在(x,y)处的灰度值,g(x,y)为图像二值化后(x,y)处像素的灰度值;T为给定的分割阈值;在二值图像中像素值为1 表示煤基质,0 为孔隙微裂隙结构。
最大类间方差Otsu 算法被广泛用于煤孔裂隙分割阈值的确定[20-24]。但针对具有单峰灰度分布图像Otsu 算法确定的阈值过大导致分割效果不理想[25],需要人为加以调控界定,增加了图像处理的主观误差。因此,采用刘江峰等[26]提出的Liu-Cao 算法对分割阈值进行修正,该算法与16 种常用的数字图像分割算法(Otsu、Yen、Triangle、IJ_IsoData、Huang 等)相比,能够准确有效提取孔隙微裂纹结构。
设灰度图像的总像素为N,图像灰阶总数为K,灰度值为i的像素总数为Qi,图像灰度分布曲线表达为:
该算法基于图像灰度分布曲线及其二次微分分布曲线进行阈值确定。如图3 所示,低阶长焰煤垂直层理与平行层理SEM 图像的灰度分布曲线均为单峰,阈值T的取值范围为
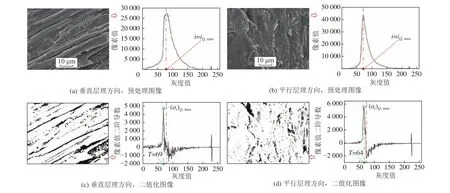
图3 阈值确定过程及二值图像Fig.3 The threshold determination process and binary image
对于含少量孔隙(微裂隙)的煤样,孔裂隙对应的像素值占像素总数的微小部分,阈值范围在灰度分布曲线上表现为像素值突增阶段,通过计算像素数量变化的二阶导数(ai)可直观看出灰度分布曲线的最大突变点,二阶导数最大值对应的灰度值i,为图像的最佳分割阈值T。对应表达式为
式中,ai为像素数量变化的二阶导数;T为图像的最佳分割阈值。
由式(3)结合灰度分布曲线得到煤样垂直与平行层理图像分割阈值范围分别为0~85、0~72,再由式(4)、式(5)计算得到灰度值二阶导数峰值,对应的灰度值即为分割阈值。垂直与平行层理方向的最佳分割阈值分别为T=69、T=64,通过图像二值化孔裂隙结构识别结果如图3c、图3d 所示。
2.1.3 形态学处理
煤样二值图像中孔裂隙呈现黑色,由于煤屑碎粒杂质及孔洞的影响,二值图像中存在大量单像素小点。通过对二值图像进行形态学处理可有效减少孔裂隙参数的统计误差。
闭运算是采用一个结构元素作为图像运算的“探针”,使结构元素对目标像素先进行膨胀遍历运算,再进行腐蚀遍历处理,从而达到填充细小孔洞,弥合微小裂隙,平滑孔裂隙边界的效果。通过选取大小为0.5 pix 的结构元素进行闭运算,然后利用Fill-Holes 模块进行单像素孔洞填充后,得到形态学处理结果,如图4 所示。形态学处理前垂直与平行层理方向图像孔裂隙数量分别为2 218 粒和1 127 粒,处理后分别为691 粒和830 粒(添加红色边框和序号进行区分),通过形态学处理有效降低了由图像杂质及噪点造成的统计误差。

图4 二值图像形态学处理结果Fig.4 Morphological processing result of binary image
2.2 煤样细观结构参数提取
2.2.1 图像分割效果验证
为验证上述图像处理方法对SEM 图像煤样孔裂隙识别的可靠性,采用现在主流的数字图像孔裂隙识别方法Otsu 算法进行识别精度对比。通过计算得到2 种算法的最佳灰度阈值,Liu-Cao 算法与Otsu 算法得到垂直层理方向的理想阈值分别为T=105、T=69,平行层理方向的分割阈值分别为T=101、T=64。为了进一步比较2 种算法分割阈值对煤样孔裂隙结构的识别效果,采用Fiji 软件中3D surface plot 模块绘制2 种阈值分割三维剖面图,结果如图5、图6 所示。对比可知,Otsu 算法几乎将整个灰度图像识别为同一连通孔裂隙,而Liu-Cao 算法可以更加精细地识别出小尺度连通或孤立孔裂隙,清晰完整地反映出煤体内部空间结构特征。从表2 孔裂隙结构参数分析可知,基于Otsu 算法计算的孔隙率高达72%以上,而Liu-Cao 算法在7.76%~14.83%,更接近煤样的真实值。煤样的孔裂隙最大面积、最大周长、最大直径参数值也远大于后者,而孔裂隙数量则显著减少。这是由于Otsu 算法对SEM 灰度图像过度识别导致大量孔裂隙被错误整合,导致孔裂隙结构参数计算值偏高。由此可知,Liu-Cao 算法识别的孔裂隙结构参数更精准,能够客观反映真实情况,孔裂隙识别可靠性更强。
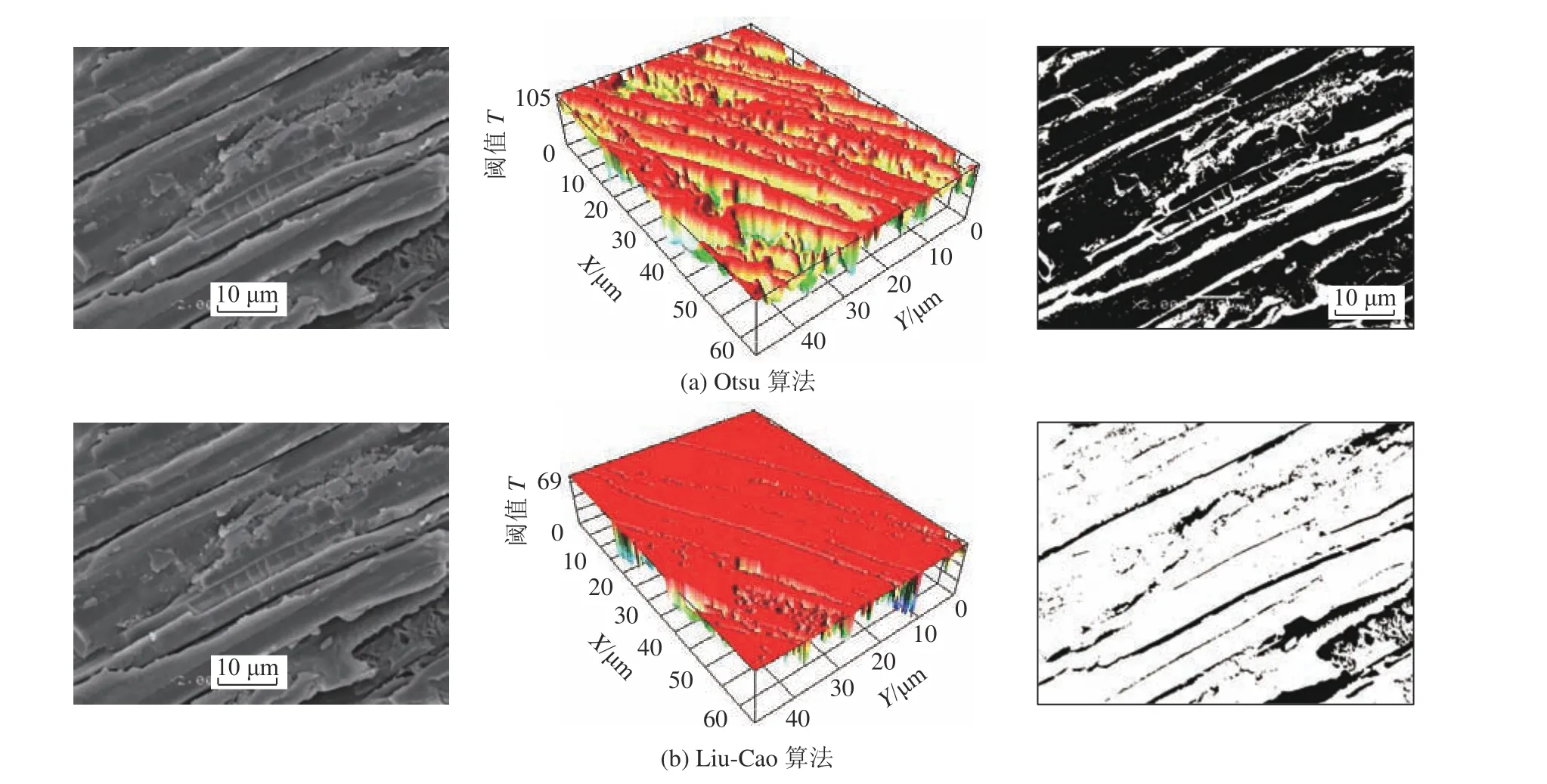
图5 垂直层理方向煤孔裂隙结构识别结果Fig.5 Identification results of coal pore fracture structure in vertical bedding direction

图6 平行层理方向煤孔裂隙结构识别结果Fig.6 Identification results of coal pore fracture structure in parallel bedding direction

表2 煤样孔裂隙结构参数对比Table 2 Comparison of fracture structure parameters of coal sample hole
2.2.2 图像特征参数提取
在形态学处理后利用Fiji 中Analyze Particles 提取煤样孔裂隙细观结构信息,本次设定获取参数为孔裂隙的数量、面积、周长、形心坐标、长度、宽度和方位角7 个参数。煤样孔裂隙细观结构参数见表3,煤样孔裂隙细观结构统计信息如图7 所示。

图7 煤样孔隙实际分布及近似概率密度函数Fig.7 Actual distribution and approximate probability density function of coal sample pores
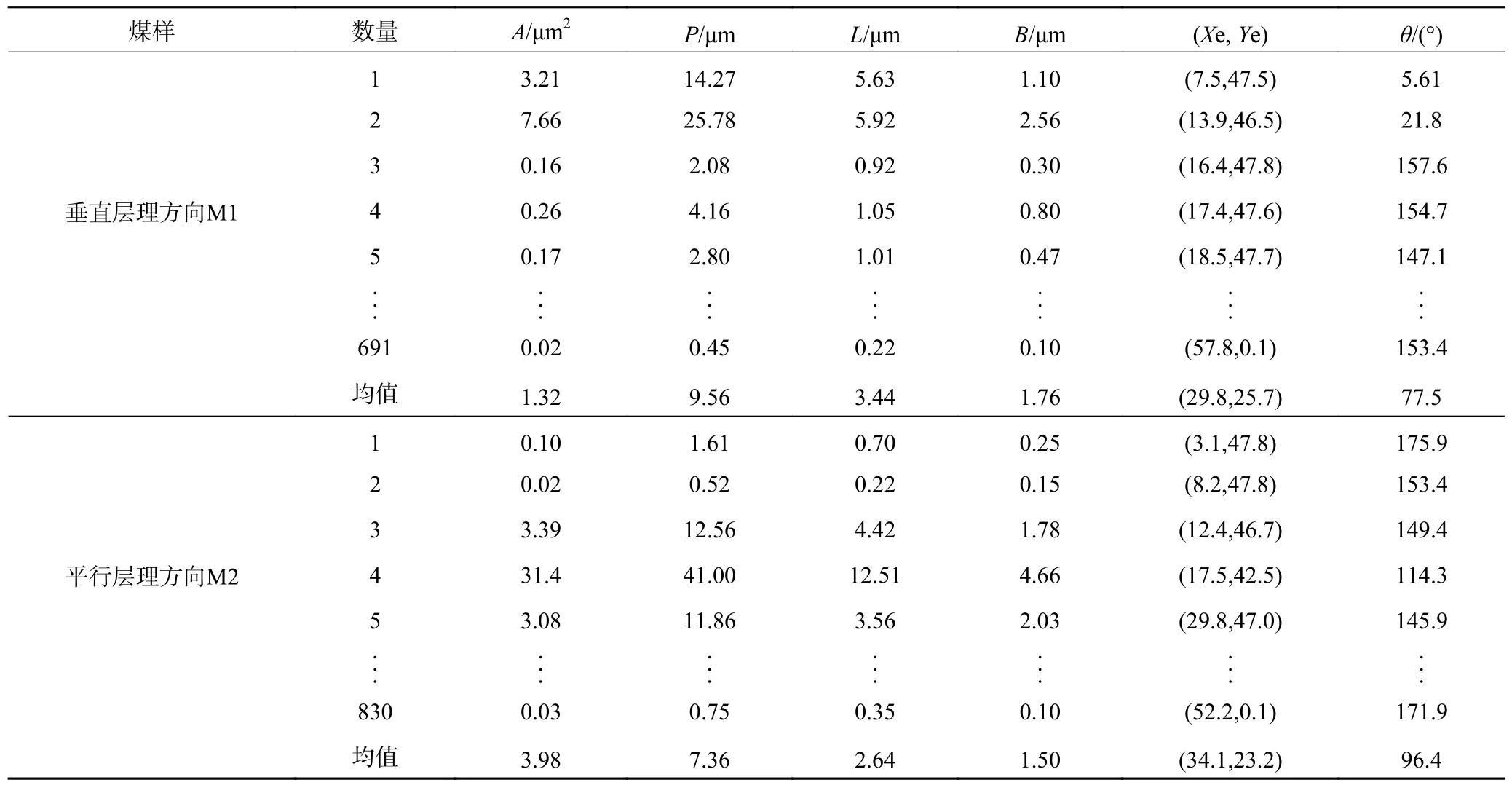
表3 煤样孔裂隙结构参数统计(一次参数)Table 3 Statistical of coal sample pore and fracture structure parameters (primary parameters)
煤样孔裂隙结构特征参数具有显著的统计规律,其中,孔裂隙面积、周长、直径服从幂函数分布,可拟合为:
式中:A、P、L分别为面积、周长、最大Feret 直径;a、b为对应的拟合系数。
3 煤样细观特征与REV 关键参数
为更好地定量表征煤体孔隙微裂隙结构特征,在煤样二值数字图像中直接提取的一次特征参数基础上进行二次处理,从孔裂隙密度、形态、分布特征3 方面构建能够反映煤样物理力学各向异性的细观定量分析指标,包括面孔隙率、整体形状因子、分形维数及定向分布系数。
煤样的REV 大小很大程度上取决于参数的选择,不同参数得到的REV 大小不等,煤体孔隙微裂隙结构的几何特征包含孔裂隙的密度、形态及方向来表征。因此,选取的REV 参数要准确地描述上述3 个方面的几何特征。在表征孔隙微裂隙结构复杂程度时引入孔隙率、形状因子、分形维数及概率熵等参数进行定量研究孔隙微裂隙的几何特征与REV关键参数确定。
3.1 孔隙率
孔隙率是衡量煤样孔裂隙结构发育程度的重要参数,可以通过计算二值图像中孔裂隙像素面积比上样本面积得到。对比分析垂直层理和平行层理方向煤样孔隙率可知:垂直层理煤样孔隙率为14.829%,约为平行层理方向的2 倍,孔隙率在不同方向上存在着明显的差异。从孔裂隙数量上看,前者的孔隙数量(691 粒)却少于后者(830 粒)。这说明孔隙率与孔隙数量没有必然的正相关关系,但与孔径大小的贡献率有关。因此,需要进一步分析孔径与孔隙率的变化情况。
孔径结构划分标准采用Xoдoт (1961)提出的十进制孔隙分类方法[27],分别以10、100、1 000 nm 为界将煤样孔径划分为微孔、过渡孔、中孔和大孔4 类。利用等效面积和等效周长对孔隙进行分类,主要研究中孔(含过渡孔)和大孔对孔隙率的贡献率,中孔和大孔的临界面积为0.785 μm2,临界周长为3.14 μm。垂直层理和平行层理方向煤样孔隙实际分布及近似概率密度函数如图7 所示,煤样孔隙面积、周长及Feret 直径均服从幂函数分布,根据孔隙面积概率分布函数可以计算出指定孔隙面积的分布概率。
由图7a、图7b 可知,垂直层理煤样中孔占比91.61%,对孔隙率的贡献率为14.30%,大孔占比8.39%,贡献率为85.70%;平行层理煤样中孔占比94.22%,对孔隙率的贡献率为34.15%,大孔占比5.78%,贡献率为65.85%。2 种煤样孔隙率不同但孔隙占比相似,说明煤样的孔隙率主要取决于大孔的数量。通过对比以面积、周长和直径进行划分的孔隙统计图,采用不同方法分割得到的中孔和大孔占比不同,这主要与孔隙的形态有关,故仅选择孔隙率作为确定煤样REV 的参数是不全面,需要对孔裂隙的其他参数进行研究。
3.2 孔隙形态
孔隙形态分为整体形态和边缘形态,是影响煤体孔裂隙扩展、变形和力学性质的重要参数。整体形态包括孔裂隙的延性(伸长属性)和多边形态;边缘形态则表现为孔裂隙的边界曲线特征即边缘粗糙度。煤样孔裂隙形状具有多样性,孔隙边缘形态具有不规则形,且表现出一定自相似性。因此,引入形状因子与计盒维数来表征孔隙的整体形态和边缘形态。
3.2.1 整体形态
在综合考虑长径比、凸度、球形度及圆度的基础上,涂新斌等[28]通过对比不同形态描述参数确定了整体形状因子Fs与实际形态较为符合,形状因子由周长和面积定义为:
式中:S为形状因子;P为孔隙周长。
形状因子反映孔裂隙的整体形态,系数越接近1 孔裂隙越接近圆形,当低于0.886(表示为正方形)孔裂隙存在明显的锐角,孔裂隙整体形态的不规则性随着形状因子系数的增高而降低。
从图8 中可以看出,垂直层理煤样孔裂隙形状因子系数为0.165~0.997,平均值0.760,形状因子大于0.886 占比35%;平行层理煤样孔裂隙因子系数为0.275~0.999,平均值0.780,形状因子高于0.886占比37%。与垂直层理煤样相比,平行层理方向煤样孔裂隙更加浑圆,其原因在于垂直层理方向煤样微裂隙较为发育,沿着孔隙尖角端扩展成为狭长的条状微裂隙。因此,孔裂隙扩展方向在一定程度上影响着孔裂隙的整体形态和分布密度。

图8 形状因子统计结果Fig.8 The data of shape factor
3.2.2 边缘形态
计盒维数(Box counting dimension)对于具有一定自相似的图形,能够有效描述其局部和整体之间复杂程度。
根据计盒维数统计原理,采用不同步长δ的网格盒子覆盖孔裂隙结构并统计所需盒子总数N(δ),分别对盒子步长与总数取对数,即可得到lgN(δ)-lgδ双对数线性关系。其拟合直线斜率就是孔裂隙结构的分形维数D。
图9 展示了不同层理煤样孔裂隙结构的分形维数分布情况,垂直层理煤样孔裂隙分形计盒维数D=1.954,平行层理煤样为D=1.964。可见,整体形态更加浑圆的平行层理煤样孔裂隙的边缘形态更加复杂。因此,仅用整体形状因子表示孔隙形态是不全面的,同时考虑整体与边缘形态的方式能更好表征煤样孔裂隙的形态参数。

图9 分形盒维数数据统计结果Fig.9 The data of box fractal dimensions
根据上述煤样孔裂隙形态分析结果,垂直层理方向的整体形状因子、分形维数均小于平行层理方向。与平行层理相比,垂直层理方向孔裂隙规则性较差,比表面积较大,空间充填能力较强,但边缘光滑性却优于平行层理方向,这是由于孔隙尖角端扩展成为狭长的条状微裂隙过程中平滑了孔裂隙边缘形态所致。
3.3 孔隙方向
以图像的横轴为基准方向,测量出孔裂隙最大Feret 直径方向与横轴的角度值,视为该孔裂隙的定向分布角。因为0°~180°和180°~360°具有对称性,所以选择0°~180°作为孔裂隙角度的统计范围。以10°为标准将方位角分为18 个角度间隔,Pi表示每个间隔内孔裂隙出现的频率。
不同层理煤样孔裂隙的方位分布情况如图10所示,垂直层理煤样孔裂隙方向主要集中在0°~60°,定向频率达到了55%;平行层理方向主要分布在60°~120°,定向频率达到了51%。由此可以看出,孔裂隙空间展布情况存在较大差异,从最大定向频率来看,垂直层理方向为20°~30°,平行层理方向为90°~100°。究其原因主要是由单轴压缩时试件受力方向和层理方向的不同而导致的。在确定煤样REV 的关键参数中,孔裂隙定向分布参数可以描述孔裂隙在变形过程中的孔隙扩展方向。因此,定向参数的研究对REV 的确定尤为重要。孔裂隙的定向分布程度可以用概率熵来表征,其定义[29]为:

图10 孔裂隙方向空间分布Fig.10 Spatial distribution of pore fracture direction
式中:H为概率熵,0≤H≤1;Pi为第i个特定范围内孔裂隙的定向频率,n取18。当H=0 时,孔裂隙方向一致;当H=1 时,孔裂隙处于随机方向。概率熵的值越大,孔裂隙定向分布程度越高,排列方向越混乱[30]。
通过计算得到,垂直层理方向概率熵为0.951,平行层理方向为0.973,垂直层理方向煤样孔裂隙的排列更趋于简单、整齐和有序性。
基于以上分析,煤样孔裂隙结构的孔隙率、形状因子、分形维数及概率熵能够准确的表征煤体细观结构的几何特征,可作为本次确定煤样几何REV 的关键参数。
4 基于煤样细观结构的REV 确定
4.1 REV 确定的采样方法
煤是一种具有强烈非均质性与各向异性的多孔介质岩体。为获取煤样不同位置与不同层理方向的细观参数,取不同位置的9 个煤样进行单轴压缩试验,并从破坏煤样不同高度等距选取破裂方向各异的煤块,制成大小为(5±2) mm 切片进行扫描电镜试验。经过第2.1 节图像处理获得了5 种放大倍数下的二值图像,用于煤样细观结构REV 的确定。
在考虑非均质性和各向异性的制样方法后,借鉴CLUNI 等[31]的有限尺度测试窗法,如图11 所示。放大200 倍的二值图像尺寸为480 μm×640 μm,从图像对角线方向的左上角(Dl)、右下角(Dr)为起点,以20 μm 为恒定步长逐级选取24 级取样窗口,以获得不同尺寸的图像样本。9 个煤样共获得432 个图像样本,最小样本尺寸为20 μm×20 μm,最大的为480 μm×480 μm。值得注意的是,不同放大倍数图像包含的孔裂隙数量以及边缘形态清晰度不同,为了精准获取每一层级孔隙微裂隙结构几何特征,分别从5 种放大倍数的图像中提取对应窗口的特征参数。

图11 煤体细观结构REV 单元的选取Fig.11 Selection of REV unit of coal micro structure
4.2 REV 确定的定量方法
目前,REV 确定的量化方法主要有直观判断法、数理统计方法及其他分析方法[32-33]。直观判断法是通过绘制煤样选定参数随研究尺度的变化曲线或散点图,从图上参数的变化趋势是否趋于稳定来确定REV 的大小。这种方法简单便捷,但具有较强的主观臆断性,REV 结果因人而异。数理统计方法有梯度误差分析、变异系数判别法及假设检验法等。其他分析方法包括曲线拟合法、灰度关联分析及人工神经网络算法等。相较几种方法而言,数理统计方法更为科学严谨,其可信度有更高的保证。
为减少人为主观判断误差,引入变异系数(CV),即标准偏差与平均值的比值,以量化选定参数的离散性。CV 值越大,参数值的离散性越显著,REV 的尺寸越小。在以往的研究中,Min 等[34]和Esmaieli等[35]分别以5%、10%、20%作为可接受的CV 值,在此基础上MA 等[36]选取中间值(10%)来确定REV 的大小,取得良好的结果。鉴于此,采用10%作为可接受的变异系数。
4.3 考虑非均质性和各向异性的REV 确定
在考虑煤体非均质性与各向异性的采样基础上,获取了煤样孔裂隙几何参数用以REV 大小的确定。计算出煤体不同尺度单元细观结构的特征参数值,分别绘制了4 种特征参数值随样本尺寸变化的散点图及对应的CV 曲线,如图12 所示。
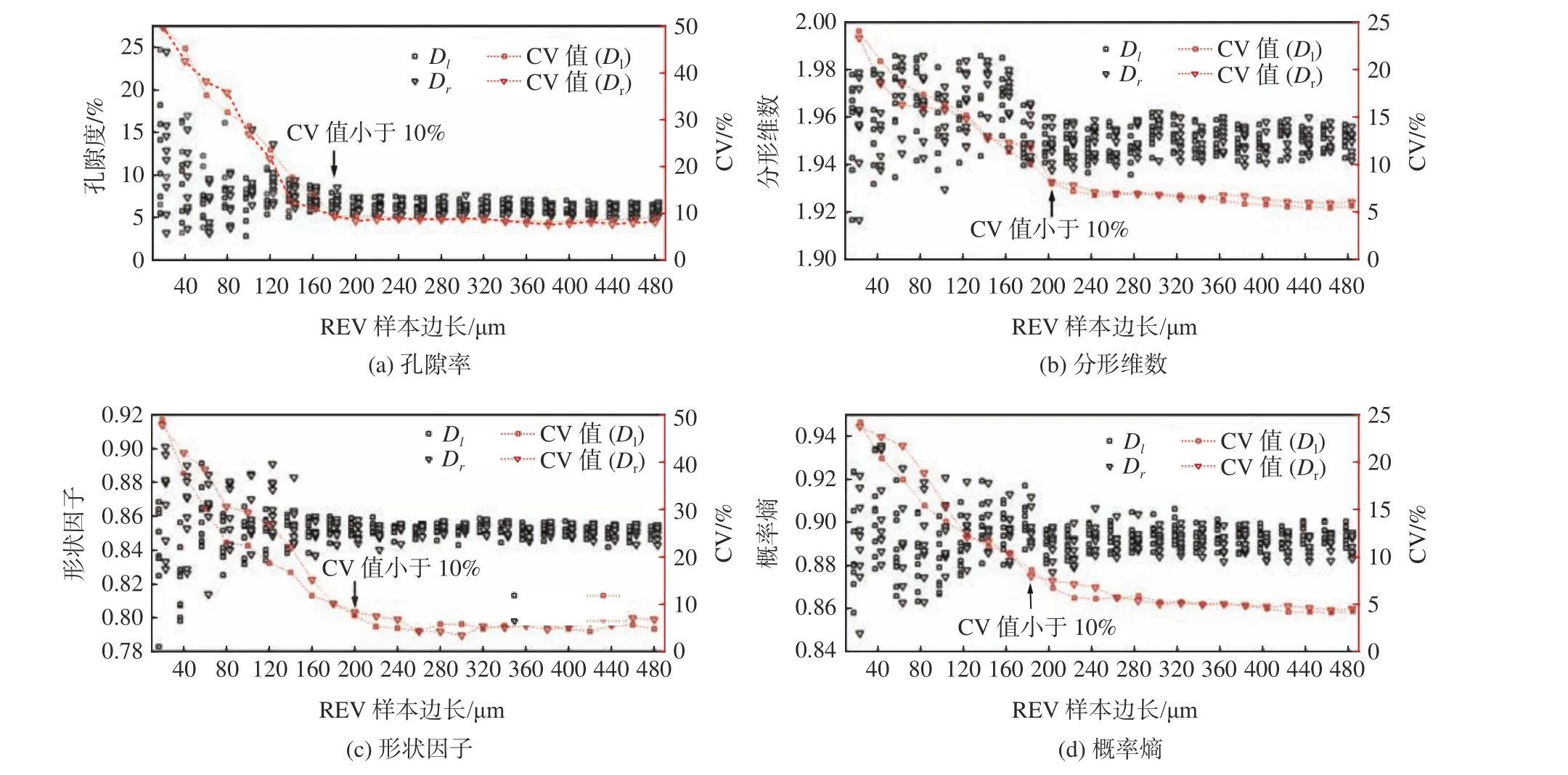
图12 煤体细观结构特性参数值和CV 值Fig.12 Micro structural characteristic parameter values and CV values of coal
图中同一尺度下煤样参数值的波动性对应着孔裂隙结构的不均匀性,而图像2 个方向(Dl与Dr)获得的CV 值变化情况体现了煤样的各向异性。特别是Dr方向的整体形状因子和分形维数均大于Dl方向,由此可见,煤体细观结构几何参数具有显著的方向效应,且在20~120 μm 尺度下表现出极强的非均质性和各向异性特征。当样本尺寸较小时,参数值在图中的位置波动变化很大,随着样本尺寸增加,参数值的变异性逐渐减弱,即CV 值逐渐降低。各参数值随尺寸的变化分为2 个明显的阶段:微观波动区和收敛稳定区,其特性参数的临界值即可称为表征单元体REV,当研究尺度大于REV 值时,在误差允许范围内可采用确定的REV 的参数描述煤体细观结构的几何特性。
基于变异系数确定的煤体细观结构REV 尺寸见表4,REV 尺寸因参数而异,当变异系数的CV 值为10%时,基于孔隙率、整体形状因子、分形维数和概率熵确定的REV 尺寸分别为180、200、200、180 μm,在多重参数下取最大的200 μm 作为煤样的REV 的尺寸。因此,所确定的煤体扫描电镜下细观结构REV 尺寸为200 μm×200 μm,即REV 尺度下煤体细观结构具有代表性。

表4 基于变异系数的煤体细观结构REV 尺寸Table 4 REV dimensions of coal meso-structure based on coefficient of variation
5 结 论
1)提出了针对煤样SEM 图像孔裂隙细观结构定量表征方法,通过提出的图像预处理、最佳阈值分割及形态学运算方法,可实现煤样SEM 图像孔裂隙结构的准确识别和定量分析。
2)针对煤样孔裂隙结构特征参数,从密度、形态、分布特征方面构建了反映煤样物理力学各向异性的细观定量表征指标。基于孔裂隙特征参数统计分析发现,孔裂隙面积、周长、Feret 直径服从幂函数分布,与平行层理相比,垂直层理方向微裂隙更为发育,孔隙率为平行层理的2 倍,空间充填能力较强,孔裂隙整体形态规则性较差,但边缘形态光滑性较好,定向分布更简单。
3)通过煤体细观结构特征分析,采用孔隙率、形状因子、分形维数及概率熵能够准确地表征煤体细观结构的几何特征,以此为基础确定的REV 更加合理有效。
4)在考虑煤体非均质性和各向异性的采样方法的基础上,取CV 值10%确定了煤体细观结构表征单元尺寸为200 μm×200 μm,即该尺度下的煤体细观结构特征具有代表性。

