基于解耦计算的多步快速成形有限元法*

鲍益东，席 洁，秦雪娇，刘永财

（1.南京航空航天大学，南京 210016；2.常州工学院，常州 213032）

钣金件有着强度高、重量轻、性能好、可大规模量产的优点，并且成形钣金件比常见的机械减材加工工艺具有更高的加工效率和材料使用率，因此被广泛应用于航空、航天、汽车、船舶、电子器件等工业产业。随着现代飞机产量需求的加大和制造要求的提高，飞机零部件的生产愈发精密复杂，并且生产周期短、质量要求高。钣金零件是飞机机体构成的重要零件，在飞机零件总量中可占30%～50%，冲压成形是飞机钣金件制造的关键技术之一，飞机钣金零件的生产效率和成形精度直接影响着飞机的生产周期和整机质量，因此钣金零件的生产也需要保证高质量、高精度、短周期和低成本。为了缩短钣金件的设计制造周期，节约研发成本，计算机技术和数值模拟技术逐渐应用于生产当中[1–2]。

有限元法是板材成形数值模拟的主要分析方法，主要分为基于流动理论的增量法和基于形变理论的全量法。增量法的主要优点在于模拟过程中考虑了加载历史的影响，模拟结果精度相对较高，但计算时间较长，难以满足设计阶段快速评价产品可制造性的需求[3]。法国的Batoz[4]和Naceur[5]等首先提出了基于全量理论的一步逆成形有限元法，基本原理是简化设置整个成形过程，将零件的最终形态和初始板料形态进行对比，简单且快速地求出零件最终形态的应力应变分布以及初始板料形状。Li 等[6]提出在一步逆成形有限元法中用小应变方程解决大变形问题。我国对一步逆成形有限元法的研究从20世纪90年代开始，上海交通大学的沈启彧[7]和Wang[8]等对方盒件的成形使用一步逆成形有限元算法进行了预示。周平等[9]对一步逆成形法的求解方法进行了改进，提出一种基于切平面的解耦列式法，使一步逆成形法的计算精度得到提高。在一步逆成形有限元法的基础上，具有一定工程实用性的一步正成形有限元法发展起来，与一步逆成形有限元法相比，一步正成形有限元法的求解过程更加符合零件的实际成形过程，根据规则的初始坯料计算得到成形后零件的形状。一步成形有限元法 （包括一步逆成形和一步正成形）计算效率虽然很高，但是由于计算过程中采用了过多的简化处理与条件假设，忽略了变形历史，使得应力计算的精度无法达到预期。为了改善这一现状，研究人员多采用引入中间构形的方式来模拟成形过程中的变形历史。Lee 等[3]在单步逆成形法基础上提出了多步逆成形法，通过线弹性映射法计算成形过程中的中间构形，并根据数值结果验证了可行性，但对于复杂零件难以找到对应的映射函数进行计算，具有一定的局限性。Guo 等[10]提出伪逆成形法，采用最小面积法构造成形加载过程中的中间构形，但只考虑轴对称问题，对于非对称问题并不适用。唐炳涛等[11]采用双截面法和单元面积最小的方法求解中间构形初始解，可以求解非对称问题，但是容易出现局部网格严重畸变的问题。陈伟等[12]对多步正成形算法中的中间构形初始解预示算法进行研究，将初始平板料投影到最终构形上后，采用比例插值的方法计算出中间构形，并对中间构形进行接触修正。

目前，国内外对中间构形基本理论的研究尚未成熟，在构造复杂形面的中间构形时仍然存在一些问题，对于构形间应力更新算法方面的研究相对更少，因此要做到高效准确地预示中间构形，从而提高零件成形模拟的精度仍然需要更加深入透彻的研究。

本文在一步快速成形有限元法（一步正成形有限元法）的理论基础上，研究多步快速成形有限元法，提出了一种基于解耦格式的中间构形预示算法，将中间构形的求解过程解耦为弯曲变形和拉伸变形两个阶段，解决了迭代求解复杂非线性方程组容易出现病态矩阵的问题，提高了求解效率，并且可以适应复杂零件形状的求解。最后，通过实际数值算例验证了该算法的有效性和准确性，可以用于指导钣金件的实际生产。

1 一步快速成形有限元法基本理论

一步快速成形有限元法基于全量理论，将零件成形过程简化为近似比例加载的过程，只考虑初始板料构形及最终零件构形两种状态，其基本思想为：从板料的初始构形C0出发，C0上各节点P0的坐标已知，在满足一定边界条件的情况下，通过有限元方法可以确定与初始板料上各节点P0对应的最终构形C上的节点P的坐标，对比两者坐标的变化可以获得成形后零件的应力应变状态以及厚度分布情况，如图1所示。

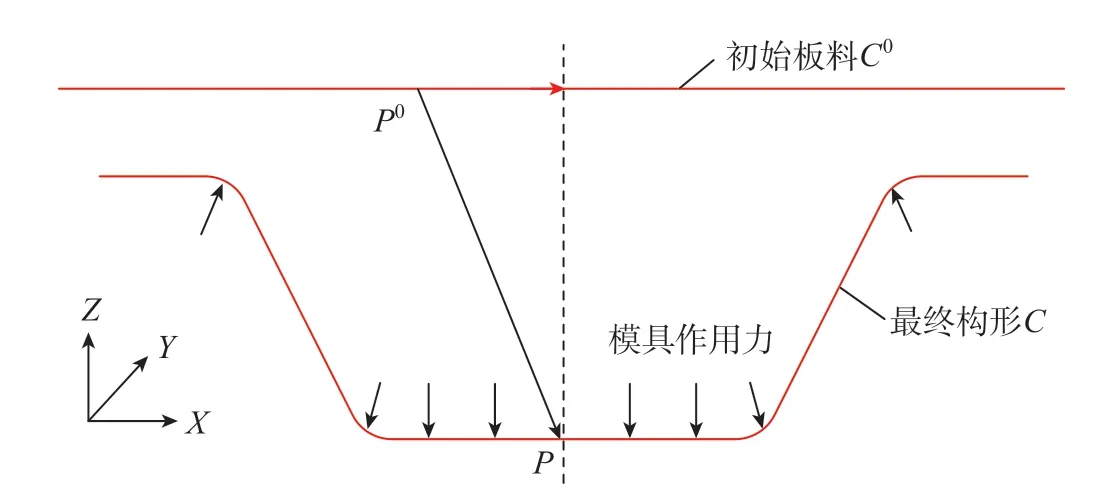
图1 一步快速成形有限元法示意图Fig.1 Diagram of one-step quick forming finite element method

1.1 几何关系

一步快速成形有限元法假设板料的变形满足Kirchhoff假设，则初始板料和最终零件构形上的任意质点的几何关系如图2所示 （其中，Up为质点p的位移函数，即质点p和p0之间的位移向量；n为质点p的单位法向量；n0为质点p0的单位法向量；z为q点的厚向坐标；z0为q0点的厚向坐标；h为最终构形的板料厚度；h0为初始板料厚度）。将初始状态板料作为参考构形，比较当前构形与初始构形上对应的质点 （如质点q和质点q0）的位置坐标，即可得到相应质点的位移函数Uq，即

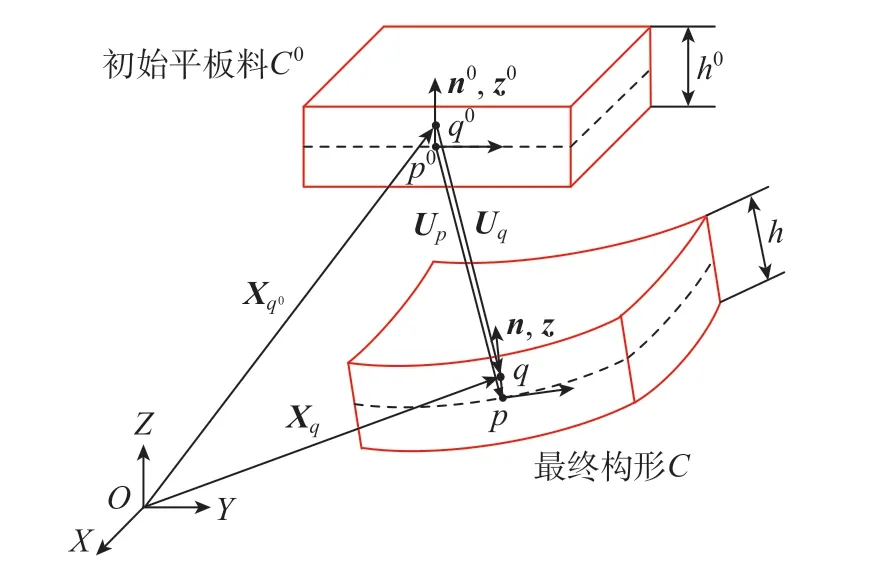
图2 一步快速成形有限元法的几何关系Fig.2 Geometric relations of one-step quick forming finite element method

式中，Uq=[U1U2U3]T；Xq=[XqYqZq]T；Xq0=[Xq0Yq0Zq0]T。Xq和Xq0分别为q点和q0点的坐标向量。

采用Lagrange 描述质点的运动，则有

式中，[F]为变形梯度张量，由此可得左柯西–格林 （Cauchy–Green）矩阵[B]的逆矩阵为

对于当前构形材料内部任一点来说，可以用3 个主方向上的主伸长量来描述这一点的变形。通过计算[B]–1的特征值可以得到板料上各点的面内主拉伸λ1、λ2，然后通过体积不变的原理可以得到单元厚度方向的主拉伸λ3为

单元应变的主方向是由[B]–1的特征向量决定的，即

式中，[M]为单元应变方向向量矩阵；n1、n2、n3分别为单元应变3 个主方向的单位向量。

最终可以得到单元沿厚度方向任意一点变形的对数应变为

1.2 本构关系

一步快速成形有限元法的本构方程是采用比例加载条件下的全量形变理论描述的，并将材料的各向异性特性考虑在内，本构方程为

式中，{σ}为应力矩阵，{ε}为应变矩阵；Es为材料应力–应变曲线的割线模量，即等效应力与等效应变的比值；矩阵[P]由面内各向异性系数R0、R45、R90求得，即

1.3 有限元方程的建立与求解

根据虚功原理在最终构形上建立平衡方程，即

式中，W为单元虚功；e为单元编号；{U*}为全局坐标系下的虚位移；为节点内力向量；为节点外力向量。

将所有的节点内力向量和节点外力向量组装在一起即可获得整体残余力向量，即

一步快速成形有限元法具有强烈的非线性特征，一般采用牛顿–拉普森 （Newton–Raphson）方法进行迭代求解，即

式中，{Ui}为第i个迭代步的近似初始解；ωi为引入的迭代松弛系数，以保证求解能够顺利收敛。

根据一步快速成形有限元法的实际计算情况，选择位移准则和残余力准则进行收敛性的综合判断，若迭代步小于设定阈值且迭代计算过程满足任何一个收敛准则，则认为迭代收敛结束计算。

2 基于解耦计算的多步快速成形有限元法

一步快速成形有限元法只考虑初始板料构形和最终零件构形，忽略了变形的中间状态，计算效率得以大幅提高，可以快速获得成形后零件的应力应变状态和厚度分布情况，但是对中间加载历史的忽略也会导致最终零件分析精度不足。为解决这一问题，提出了多步快速成形有限元法，通过引入中间构形的方式考虑加载路径和变形历史从而提高计算精度，每一个中间构形都作为当前时间步的最终构形通过一步快速成形有限元法进行迭代计算。因此，多步快速成形有限元法的关键在于准确地构造每个时间步的中间构形，以及各中间构形之间的应力迭代更新。

对金属薄板成形来说，变形主要由弯曲变形和拉伸变形构成，由于剪切变形对整个板料成形结果影响比较小，可以忽略其影响效应。在多步快速成形有限元法中，中间构形的计算被分解为弯曲变形和拉伸变形的解耦形式，其中对弯曲变形起主要作用的是弯曲刚度，对拉伸变形起主要作用的是膜刚度。通过解耦技术，首先进行弯曲变形过程的求解，获得板料在当前模具作用下的构形，如图3（a）所示；其次是进行拉伸变形过程的求解，在上一步求解出的板料构形的基础上，限定材料的非线性流动在该构形上，通过弹塑性流动力学进行迭代求解来获得当前时间步的中间构形，如图3（b）所示。

图3 解耦计算原理示意图Fig.3 Diagram of principle of decoupling calculation

2.1 中间构形滑移约束面的构造

板料弯曲变形的求解过程就是板料中间构形滑移约束面构造过程，假设已计算出上一个时间步的板料构形，则在该构形的基础上计算当前时间步的中间构形。其首要问题是准确地得到板料和模具的接触状态，其中包括确定凸模、凹模、压边圈等工具与板料的接触状况，只有正确地判断出与模具相接触的板料节点，才能为中间构形的预示算法提供计算依据。由于板料和模具的接触状态仅被用来计算板料的形状，所以只需判断哪些板料节点与工具发生接触，而不用进一步判断板料节点在工具表面是发生滑动还是固定不动。在判断板料节点与模具接触状态时，首先要通过搜索算法确定板料节点沿法线方向在模具表面上的投影单元，然后进一步确定具体的投影点。在接触搜索阶段，为了缩小搜索范围，加快接触搜索的速度，采用划分空间格的方法搜索距离板料节点最近的模具节点，根据节点与单元之间的拓扑关系确定模具表面的投影单元范围。

确定了板料节点在模具表面的投影点后，根据几何关系判断节点是否穿透模具表面，如图4所示。节点穿透量计算方程式为

图4 节点穿透判断示意图Fig.4 Diagram of node penetration judgment

式中，g（xs）为节点xs的穿透量；xs为板料上某一节点；xm为节点xs在模具表面的投影点；n（xm）为节点xm所在投影单元的外法线方向。

当g（xs）＞0 时，表明板料节点xs并未穿透模具表面；当g（xs）＜0 时，表明板料节点xs穿透模具表面。判断出所有发生穿透的板料节点后，将其沿节点法线方向直接投影到工具表面，假定这些发生穿透的板料节点就是可能与工具发生接触的节点，根据发生接触的板料节点会与工具表面产生作用力的特点排除其中一些误判的板料节点，剩下的发生穿透的板料节点则是真正与工具发生接触的板料节点。最后根据接触算法，搜索出与工具发生接触的板料节点信息，并确定出接触区域的板料构形。

在弯曲变形过程中，板料与凸凹模具接触的区域受到模具面的约束作用，未接触区域面内会存在膜面的初始应力而不承受其他力的作用，因此非接触区域的构形采用基于预应力膜单元建立平衡方程的方法进行计算。预应力膜单元顶点的位移向量为a=[uvw]T（其中u、v和w分别为x、y和z方向的位移分量）。预应力膜单元在变形过程中的几何关系为

式中，ε为应变；εL、εNL分别为线性应变和非线性应变；B为应变与位移的转换矩阵，BL、BNL分别为线性应变和非线性应变分析的矩阵项，前者与位移向量a无关，后者则是a的函数。

预应力膜单元具有大位移、小应变的特点，因此假设材料的应力–应变关系满足如下线弹性关系，即

式中，D为弹性矩阵；σ0为膜单元的预应力。

在单元所在的局部坐标系下，根据几何关系和本构关系，基于虚功原理建立平衡方程为

式中，V表示体积，对体积进行积分；B和均为位移向量的函数，=BL+2BNL。

采用Newton–Raphson 方法进行迭代求解，并根据位移准则和残余力准则进行收敛性的综合判断，若迭代步小于设定阈值且迭代计算过程满足任何一个收敛准则，则认为迭代收敛结束计算。否则，需要采用缩小步长的方法重新计算板料非接触区域中间构形。

重复上述过程，直至中间构形的所有单元都满足预应力膜单元的平衡条件，从而完成当前时间步的中间构形滑移约束面的构造。

2.2 基于滑移约束面的中间构形计算

在拉伸变形求解过程中，为了确保板料节点在平衡迭代过程中的移动始终被限定在板料中间构形上，将2.1 节计算出的中间构形作为板料拉伸变形计算过程的滑移约束面，约束板料的运动和变形。滑移约束面即节点的切平面区域，滑移约束面如图5所示。可以看出，节点坐标系定义在节点切平面上，轴为节点法线方向，单元坐标系（s，t）则定义在单元所在平面上。单元上的刚度矩阵ke和残余应力都将转换到节点坐标系下，转换公式如下：

图5 滑移约束面示意图Fig.5 Diagram of slip constraint surface

经过2.1 节中的几何迭代判断，滑移约束面上各节点与模具表面之间不会发生穿透，但在模具表面上圆角较小的地方，滑移约束面的网格单元会出现穿透模具表面的情况，如图6（a）所示，因此，中间构形上的节点虽然被约束在滑移约束面上，但在基于滑移约束面进行迭代计算时，节点在滑移约束面上的移动会导致中间构形上部分节点与模具表面发生穿透，需要对迭代求解的中间构形进行修正。首先按照2.1 节中的方法将约束在滑移约束面上的中间构形节点与模具进行几何接触判断，搜索到入侵至模具内部的节点，判断出中间构形上所有发生穿透的节点后，将这些节点拉回到模具表面，使其成为附着在模具表面的固定点。通过直接投影的方法将这些节点沿法线方向直接投影到工具表面，从而可以获得修正后的中间构形，如图6（b）所示。

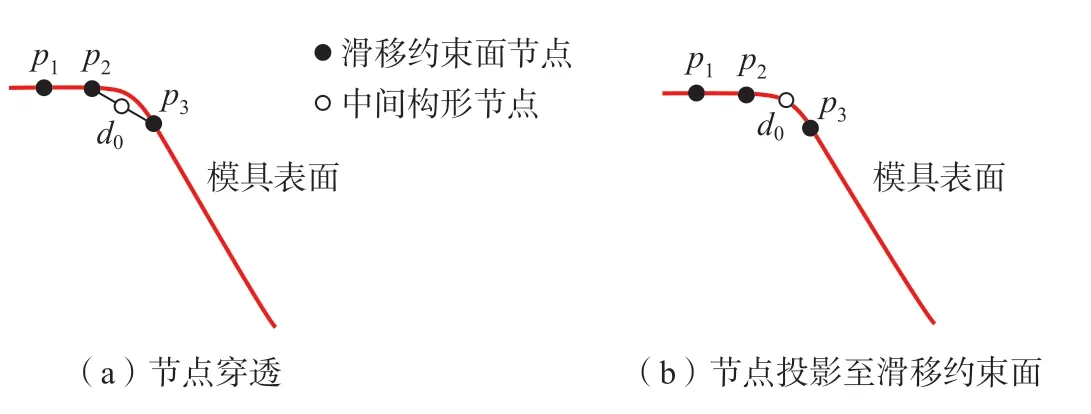
图6 中间构形修正过程示意图Fig.6 Diagram of intermediate configuration modification process

3 算例验证

本文所提出的基于解耦计算的多步快速成形有限元法算法已集成于自主开发的QuickForm 板料成形模拟软件中。为验证该算法的有效性，将计算结果与现有的基于隐式算法求解的板料成形商业有限元软件AutoForm 软件以及动力显式求解的Dynaform 软件的模拟结果进行对比分析。翼子板具有造型复杂多变、曲率变化大，表面质量和尺寸精度要求高等特点，因此成形难度大，容易出现开裂、起皱以及棱线滑移等缺陷，并且回弹量大难以准确预测[13]。以翼子板的冲压成形为例进行分析，可以充分地验证本文所提出算法的可行性。

零件所用材料为热镀锌合金钢板，材料牌号为GD53D–ZF–V22，材料参数为：抗拉强度370.4 MPa、屈服强度165.5 MPa、各向异性系数1.61、硬化指数0.22，应力–应变关系式为：σ-=502.3（0.00644+ε-）0.22MPa，曲线如图7所示。初始板料厚度为0.65 mm，初始板料划分三角形网格后如图8所示，初始单元数量为21105 个，初始节点数量为10756个，板料成形过程中可根据板料接触区域的工具表面曲率变化情况自适应加密板料网格尺寸，加密级数为3 级，板料与工具之间的摩擦系数为0.15。板料与模具的装配如图9所示，从下到上依次是凸模、压边圈、板料以及凹模，凹模向下运动，当凹模与压边圈接触后开始拉延过程，总行程为424.23 mm，压边圈行程为85 mm。采用的计算机配置为英特尔Core i5–10400@2.90 GHz 六核/12 线程的CPU，32 GB 内存。

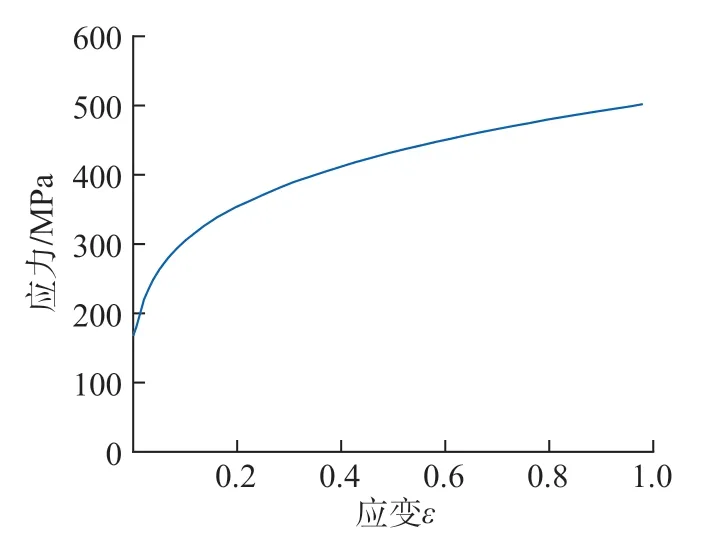
图7 材料应力–应变曲线Fig.7 Material stress–strain curve

图8 初始板料网格示意图Fig.8 Diagram of initial sheet grid

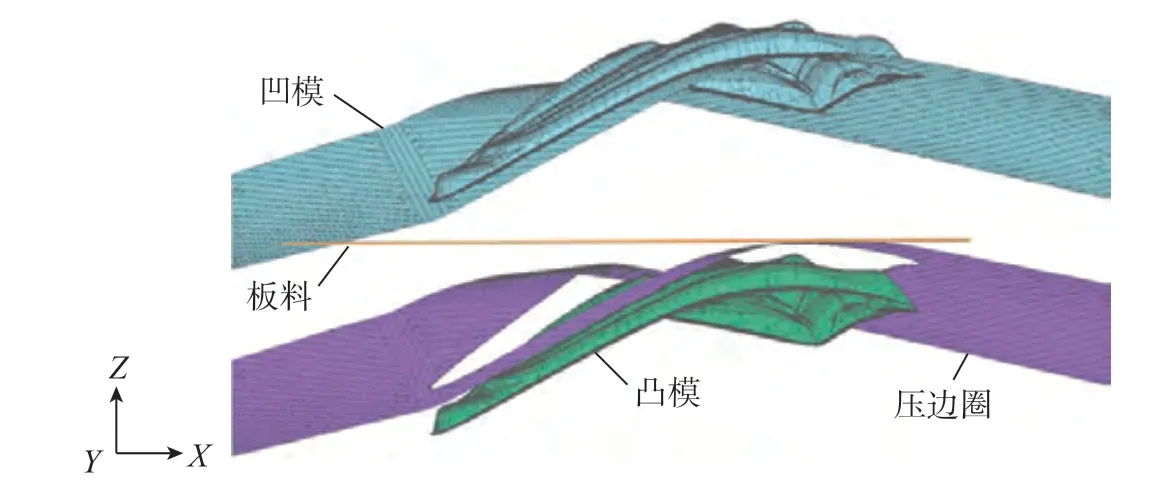
图9 板料与模具装配图Fig.9 Assembly drawing of sheet and die

拉延过程中，工具向下运动接触板料后，板料受到力的作用开始发生变形，该过程采用自适应时间步长控制，时间步长即工具向下移动的距离。有效的自动时间步长控制可以确保接触约束只在从一个增量到下一个增量之间适度改变。因此要选择合适的时间步长，既可以提高计算效率也可以减少对计算精度的影响，不会出现难以收敛的问题。本算法设置的拉延过程最大时间步长为5 mm，初始时刻步长为2 mm，发生的变形较小，时间步长自动增加为5 mm，当即将合模时，为避免迭代发散，时间步长减少至0.5 mm。每一个时间步长都对应一个经过弯曲和拉伸变形求解之后的中间构形，中间构形的变化反映了成形过程中的材料的流动情况，板料初始状态至合模状态之间若干时间步长的中间构形如图10所示。

图10 板料变形过程示意图Fig.10 Diagram of sheet deformation process

上下模距离为12 mm 时的中间构形网格如图11（a）所示，构形上特征明显的区域网格经过多次加密，节点数目较多，特征不明显的区域网格没有被加密，节点数目较少。为验证中间构形预示算法的有效性，在图11（a）所示中间构形上做纵向及横向的截面线，与AutoForm 对应位置的构形截面线进行对比。图11（b）为沿截面线AA'上分布的曲线形状，可以发现QuickForm 和AutoForm软件计算的曲线形状及拉延深度整体比较接近，但是局部区域存在一些差别。图11（c）为沿截面线BB'上分布的曲线形状，两个软件计算的曲线形状及拉延深度十分接近，说明了本文提出的中间构形预示算法是有效且可行的，能够较好地反映材料的流动情况。

图11 上下模距离为12 mm 时的中间构形形状结果Fig.11 Intermediate configuration shape results when the upper and lower die distance is 12 mm

合模状态下成形性和厚度分布对比见图12和13，其中一步快速成形有限元法与多步快速成形有限元法的最终模拟结果如图12（a）和（b）、图13（a）和（b）所示。一步快速成形有限元法没有中间构形的预示过程，因此模拟所得的零件成形性稍差，零件上特征复杂的区域成形不充分，最大厚度与最小厚度也偏大，精度稍差。一步快速成形有限元法的计算时间为29 s，多步快速成形有限元法 （QuickForm）的计算时间为216 s，QuickForm 在保证了模拟精度的情况下仍可在几分钟内完成计算，保证了求解效率。

从图12可以看出，QuickForm、AutoForm 二者成形性的整体分布情况接近，安全、变形不足，起皱趋势和趋势区的位置基本一致。从图13可以看出，QuickForm、AutoForm 模拟的板料厚度整体分布趋势一致，且最大增厚和最大减薄的位置一致。最大厚度QuickForm 的计算结果为0.691 mm，AutoForm 为0.673 mm，相对误差为2.7%；最小厚度QuickForm的计算结果为0.526 mm，AutoForm为0.499 mm，相对误差为5.4%。相较于QuickForm 和AutoForm 两种软件，Dynaform 模拟的零件整体成形性较差，变形不足的区域较大，且最大增厚和最大减薄的位置与另外两种软件相比有所差别，出现差距的主要原因是Dynaform 软件求解采用的是动力显式算法，该算法会引起惯性效应，从而使拉延结果受到影响。以上模拟结果说明了本文所提出的算法计算结果是合理可行的。在求解时间上，QuickForm 的计算总时间为216 s，AutoForm计算总时间为165 s，Dynaform计算总时间为39 min+48 s，QuickForm 计算效率要远高于Dynaform 但是略低于AutoForm 软件。QuickForm 的算法目前是单核计算，尚未实现并行求解，因此计算效率低于AutoForm，但是考虑到未来实现本文提出算法的并行计算版本后，计算效率有很大的提升空间。

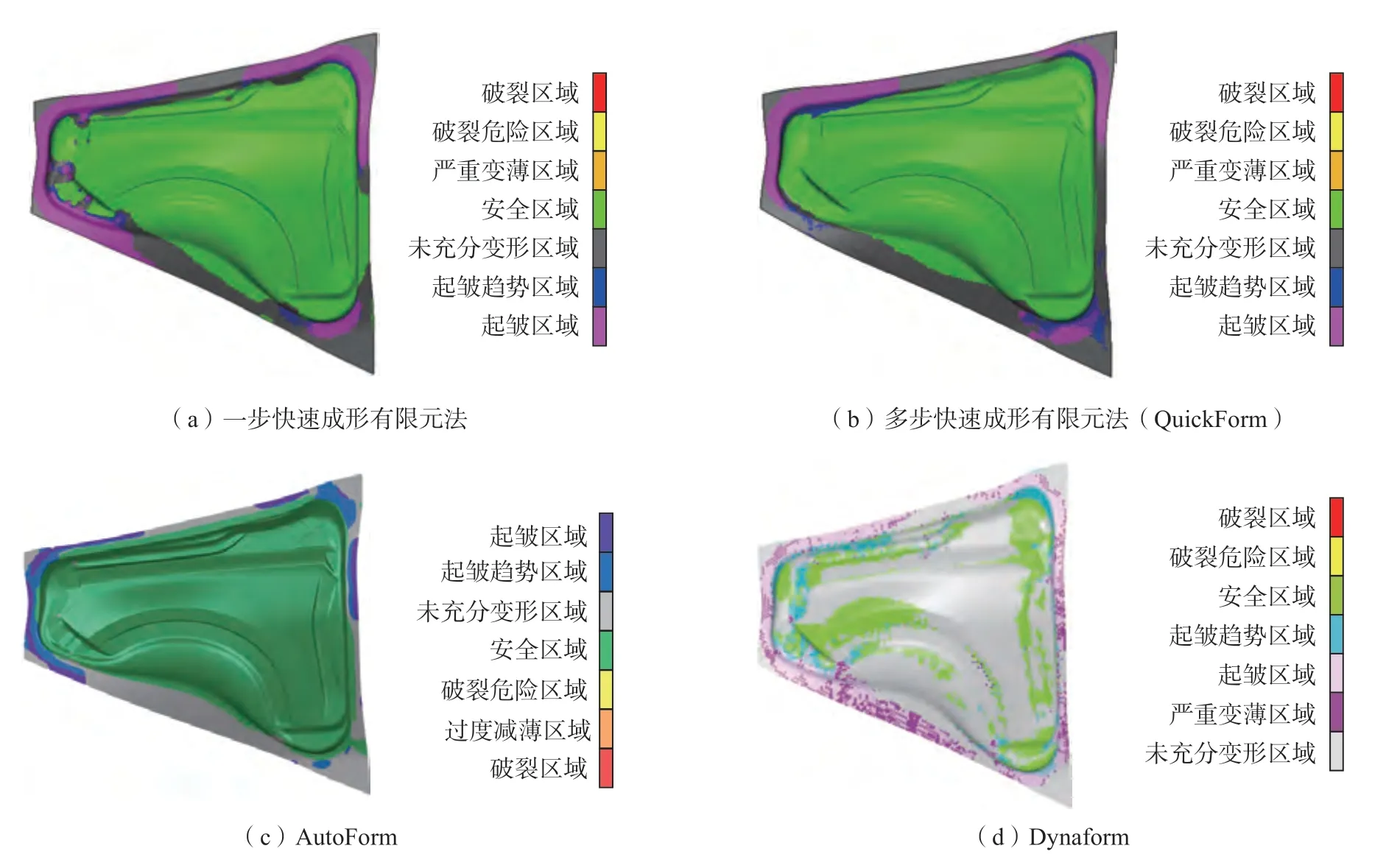
图12 合模状态下成形性分布对比Fig.12 Comparison of formability distribution under clamping state

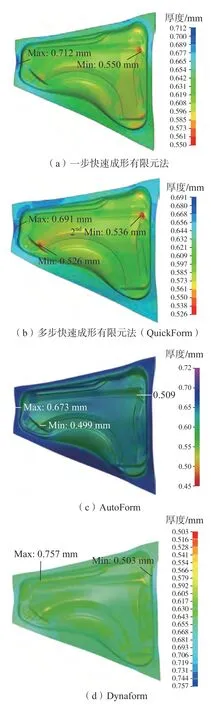
图13 合模状态下厚度分布对比Fig.13 Comparison of thickness distribution under clamping state

基于上述仿真模拟的工艺参数，进行零件的拉深成形试验，获得成形后的产品如图14所示，翼子板外观无开裂、起皱等缺陷，成形质量较好。将试验制备的最终成形零件的截面厚度分布、外轮廓线等结果与QuickForm 自研算法的计算结果进行对比，如图15所示，可以发现试验结果与QuickForm 的模拟结果基本一致，模拟精度可以满足实际生产需求。

图14 成形后的产品Fig.14 Finished product

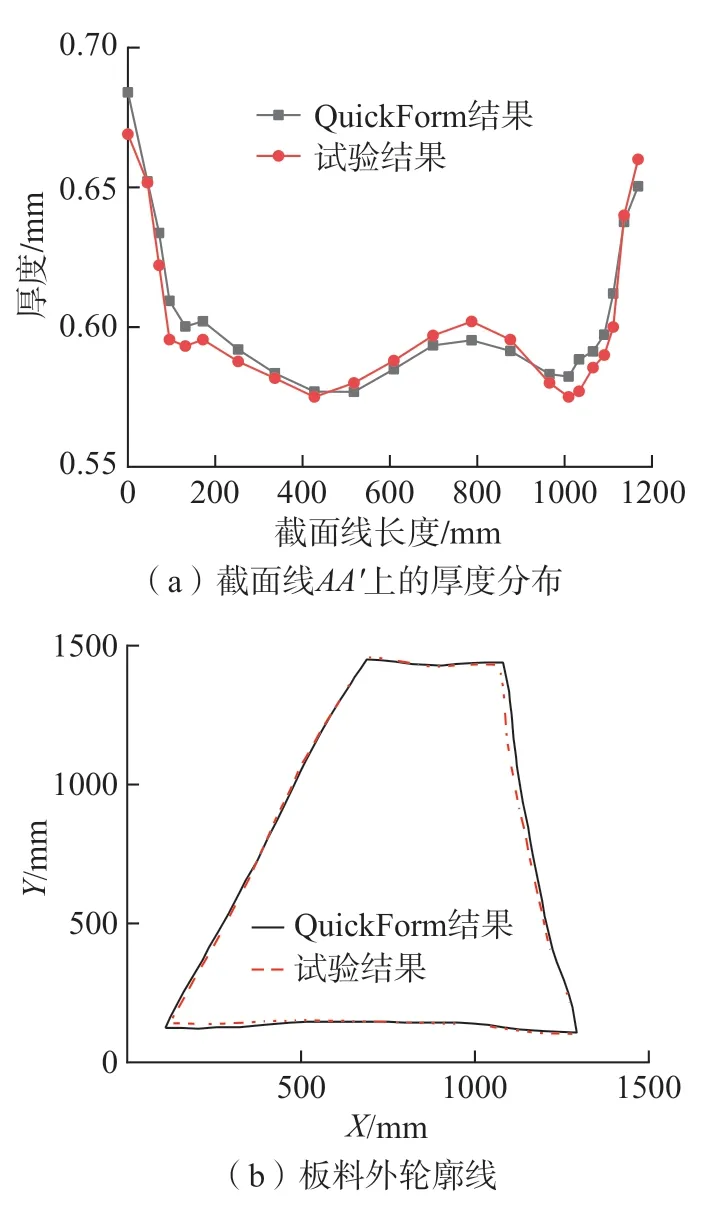
图15 最终成形零件与QuickForm 的计算结果对比Fig.15 Comparison of final formed parts and calculation results of QuickForm

4 结论

（1）在一步快速成形有限元法的基础上，引入了中间构形的多步快速成形有限元法，并提出了一种基于解耦计算的中间构形构造方法，将板料成形过程中的变形解耦为弯曲变形和拉伸变形两个过程，提高了求解效率，并通过算例的模拟结果对比验证了本文提出的中间构形构造方法的有效性。

（2）以典型钣金件翼子板为案例进行模拟分析，并将计算结果与AutoForm、Dynaform 软件的计算结果进行对比，验证了本文所提出算法对钣金零件成形预测的准确性以及高效率；在相同工艺参数下进行成形试验，试验结果进一步表明本文所提出算法的可行性，模拟精度符合实际生产要求，可以在钣金件生产设计初期进行参数优化，从而降低模具制造成本，缩短产品试制周期。