利用混杂核模糊补互信息选择特征
袁钟 陈红梅 王志红 李天瑞
(西南交通大学计算机与人工智能学院 成都 611756)
(综合交通大数据应用技术国家工程实验室(西南交通大学)成都 611756)
特征选择是一种有效的预处理方法,已经广泛应用于数据挖掘、机器学习和模糊识别等领域[1-6].其目的是剔除冗余特征以提高学习任务的泛化能力.特征选择方法的关键步骤是如何构建一个用于评价特征重要性的函数[7].这个函数可以被使用来从原始高维数据中选择一个最小的特征子集,使得数据类的概率分布尽可能地接近使用原始特征得到的分布.目前,已经有许多特征评价函数被提出,如一致性[8]、依赖度[9]和不确定性度量[10]等.
模糊粗糙集理论首先由Dubois 等人[11]提出,它是一种能处理模糊和不确定数据的有效数学工具.模糊粗糙集理论的基本思想是使用模糊相似关系来诱导模糊信息粒,这使得它克服了经典粗糙集理论处理数值属性数据需要做离散化处理的问题.因而,该理论可以直接应用于数值或混合特征数据.模糊粗糙集理论主要包括模型的扩展和应用.受原始模糊粗糙集模型的启发,提出了一系列模糊粗糙集的扩展[12-14].此外,模糊粗糙集理论也已经被应用于很多领域.特征选择是模糊粗糙集理论最重要的应用之一,已经提出了有许多基于模糊粗糙集理论的特征选择方法[15-18].这些方法可以大致分为基于模糊依赖度的[15]、基于模糊不确定性度量的[16]和模糊区分矩阵的方法[17].
信息熵起源于信息论,它能够建立一种衡量不确定性的有效机制.针对模糊关系的重要性,Yager[19]首先将信息熵的概念引入模糊相似关系中,然后讨论了模糊信息的不确定性测度.至此,在模糊粗糙集中提出了不同形式的模糊不确定性度量,如模糊信息熵[20],模糊补熵[21]、模糊粗糙熵[22]和模糊邻域决策熵[23]等.许多模糊不确定性度量已经被应用到特征选择[10,16,24-25].例如,Hu 等人[20]提出了在模糊近似空间和模糊概率近似空间中计算信息熵的广义公式并将模糊条件熵应用于混合属性约简;Qian 等人[21]将补熵引入模糊粗糙集,并提出模糊补熵的定义,但所提的模糊补熵尚未应用到属性约简中.Zhao 等人[26]在模糊粗糙集中提出了一种基于任意模糊关系的补熵模型,并将该信息熵应用于特征选择.然而,由模糊不确定性度量所定义的模糊互信息大部分都是非单调的,这可能导致一个不收敛的学习算法.此外,模糊不确定性度量的定义也不能很好地反映系统的不确定性.其原因是在计算模糊熵时,采用交运算来计算模糊相似关系.这样的计算策略可能会降低高维样本空间中模糊相似关系的辨别能力[27].因此,它可能不能真实反映样本之间的关系.
核方法把低维空间中的非线性学习问题转化为高维空间中的线性学习问题,该方法可以弥补模糊关系计算中交运算带来的不足.为此,文献[28]利用核函数生成的模糊关系粒化论域,进而构造了不同的基于核的模糊粗糙集.进一步,文献[29-30]研究了基于核模糊粗糙集的属性约简.文献[31]提出了一种基于混杂核的模糊补熵,并将其应用于无监督属性约简.然而,该文献并未定义关于决策的混杂核模糊补互信息.
基于上述讨论,本文基于混杂核模糊补熵,定义关于决策的混杂核模糊补互信息.进一步,基于所提关于决策的混杂核模糊补互信息,构建了一种考虑内外重要度的混杂特征选择评价函数.进而设计了基于混杂核模糊补互信息(kernel-based fuzzy complementary mutual information,KFCMI)的特征选择算法.最后,数据实验结果表明在大多数情况下所提算法可以选取更少的特征且能保持或提高分类准确率.
1 预备知识
在模糊信息理论中,数据表定义为一个信息系统IS=〈U,A〉.其中:U={x1,x2,…,xn}是一个非空有限对象集;A是非空有限属性集合.
设A:U→[0,1]是一个映射,则称 A是U上的模糊集.∀x∈U,A(x)称为x对 A的隶属度.论域U上全体模糊集的集合,记为F(U).设A,B ∈F(U),对任意x∈U,一些运算定义为:
一个关于U的模糊关系 R定义为U×U的一个模糊集,即R:U×U→[0,1].∀x,y∈U,如果满足:自反性(R(x,x)=1)和对称性(R(x,y)=R(y,x)),则称 R是U上的模糊相似关系.
信息熵被引入模糊粗糙集理论进行相关的不确定性测量与表示,产生了不同形式[21-22,32].Qian 等人[21]提出了一种形式的模糊补熵.设 R是U上的一个模糊关系且[xi]R表示由 R生成的广义模糊类.关于 R的模糊补熵定义为
式(1)所示的模糊补熵通过交运算来定义模糊信息粒.这样的策略可能会降低高维样本空间中模糊相似度的差异[27].因此,模糊信息粒可能不能真实反映对象的粒结构.此外,由上述模糊补熵定义的模糊补互信息是非单调的.为此,本文定义关于决策的混杂核模糊补互信息,进而构建了一种考虑内外重要度的有监督特征选择评价函数.
2 利用混杂核模糊补互信息选择特征
2.1 混杂核函数
假设U={x1,x2,…,xn},E⊆A={a1,a2,…,am}且∀xi∈U和a∈A,a(xi)表示xi在a下的取值.
现在生活中存在大量的分类、数值和混合属性数据.对于分类属性子集Ec⊆A,利用匹配核[30]来计算xi和xj关于Ec的模糊相似关系,其定义为
对于数值属性子集En⊆A,高斯核[31]被使用来抽取xi和xj关于En的模糊相似关系,其计算方式为是xi和xj之间关于En的欧氏距离;σ用于
其中调整基于混杂核的模糊近似空间的粒度,它反映了人们对数值属性中数据噪声的容忍程度.
性质1.对∀E⊆A,有
性质2.如果E1⊆E2⊆C,则
容易看到上述混杂核函数满足自反和对称的性质.因此,通过上述这些核函数计算的关系是模糊相似关系.
2.2 不确定性度量
从性质4 可以看出,在相同的属性下,较大的核参数 σ会导致更粗的粒度.σ的取值越大,则任意一对对象之间的相似程度也越大.在这种情况下,很难将任意的对象与其他对象区分开来.结果,模糊补熵越低.
当A=C∪D且C∩D=∅时,该信息系统被称为决策系统(decision system,DS),其中C表示条件属性集,D表示决策属性集.基于上述模糊补熵,∀B⊆C,以下给出关于决策属性集D的模糊补联合熵、模糊补条件熵和模糊补互信息的概念.
定义3.B和D的 模糊补联合熵定义为
定义4.D关于B的模糊补条件熵定义为
性质5.CH(D|B)=CH(B,D)-CH(B).
证明.根据定义2 和定义3,有
性质6.如果B1⊆B2⊆C,则CH(D|B1)≥CH(D|B2).
定义5.B和D的模糊补互信息定义为
性质7.设B⊆C,有3 个等式成立:
证明.由定义5,显然有CMI(B;D)=CMI(D;B),因此性质7 的等式1)成立.因为
所以,性质7 的等式2)成立.由性质5,易证性质7 的等式3)成立. 证毕.
在性质7 的等式2)中,B和D的模糊补互信息为D的模糊补熵减去D关于B的模糊补条件熵,因此B和D的模糊补互信息反映了B和D共同含有的模糊补信息量,体现了2 个属性集B和D之间相关性程度,这与其他形式互信息熵的结论是完全一致的.
性质8.如果B1⊆B2⊆C,则CMI(B1;D)≤CMI(B2;D).
证明.设B1⊆B2⊆C,则有kB1⊇kB2.由性质6 和性质7 的等式2),易证CMI(B1;D)≤CMI(B2;D).证毕.
性质8 表明模糊补互信息与特征子集大小的单调性变化.这些性质对设计一个启发式搜索算法是至关重要的.因为这保证了向已选取的特征子集中添加候选特征不会减少新特征子集的信息.因此,上述定义的模糊补互信息可以用来作为特征选择的标准.
2.3 属性重要度
特征选择的关键问题是建立属性质量的评价函数.B和D的模糊补互信息体现了B和D之间相关性程度.因此,基于模糊补互信息,分别构建了2 种属性重要度评价函数.
定义6.对∀b∈B,属性b在B中相对于D的 内重要度定义为
定义7.对∀b∈C-B,属性b在B中相对于D的 外重要度定义为
由性质8,sigin(a,B,D)越高,表示a越重要.
如果sigin(c,C,D)>ε,属性c是 ε-必不可少的,也就是说,c是一个 ε-核属性.
定义8.C的核属性集定义为
基于核属性的启发式属性约简算法可以通过将选定的属性逐步添加到核属性集中来找到一个属性约简.下面是基于模糊补互信息的约简定义.
定义9.设B⊆C,B称为C的一个 ε-约简,如果B满足2 个条件:
其中:条件1)保证所选属性子集与整个属性集在ε-误差之内具有相同的区分能力;条件2)通过删除选定属性子集中的每个属性,确保其所有属性在 ε-误差之内都是不可缺少的.
2.4 相关算法
基于定义6 和定义7 的2 种重要度,设计一种用于特征选择的启发式算法并分析其运行的复杂度.算法1 以空集为起点,首先通过内重要度计算核属性集;然后以核属性集为基础,每次计算全部剩余属性的属性重要度,从中选择重要度值最大的属性加入核属性集中,直到所有条件属性集和约简集的决策模糊补互信息之差小于等于ε.
算法1.KFCMI 算法.
在算法1 中,步骤②~④的循环次数为m,步骤③的循环次数为n×n,步骤⑤~⑪的循环次数为m,步骤⑫~⑱的循环次数为h.从而,算法1 总的循环次数为m×n×n+m+h.因此,在最坏的情况下,算法1 的时间复杂度为O(mn2).
3 实 验
在这部分,为了验证所提算法的可行性和有效性,将本文所提算法与基于模糊信息熵(fuzzy information entropy,FIE)[17]的算法、基于模糊粗糙集的特征选择(fuzzy rough-based feature selection,FRFS)[33]、基于模糊区分矩阵的属性约简(fuzzy discernibility matrix-based attribute reduction,FDMAR)[34]、适应模糊粗糙集(fitting fuzzy rough sets,FFRS)[18]和基于区分邻域数的特征选择(discernible neighborhood countingbased feature selection,DNCFS)[35]进行了分类实验的对比分析.
3.1 实验准备
实验使用了15 个数据集,它们是从UCI 机器学习库①http://archive.ics.uci.edu/ml中挑选出来的.这些数据集的基本信息如表1所示.对于一些数据集中存在的缺失值,本文采用最大概率值法来填补缺失值.此外,所有的数值属性值通过最小-最大标准化归一化为区间[0,1].
分类回归树(classification and regression tree,CART)、朴素贝叶斯(naive Bayes,NB)和k-最近邻(k-nearest neighbor,kNN)被使用来评估这些对比算法的分类效果.所有分类实验通过10 折交叉验证来实施,分类准确率的平均值和标准差作为最终结果.

Table 1 Basic Information of Datasets表 1 数据集的基本信息
在实验中,KFCMI 算法中有2 个参数 σ和ε.引入参数 σ控制样本模糊相似度,这对算法的性能有很大的影响;而参数 ε为算法的停止条件.对于给定的数据集,如果参数 ε的值变小,所选特征数不会减少.一般来说,不同的 σ和 ε会导致不同的分类准确率.因此,通过调整参数值,使 σ在0~1 之间变化,步长为0.02,且ε ∈{10-3,10-4},为每个数据集选择一个最优特征子集.在FFRS 算法中引入了2 个参数 ε和 λ.遵循文献[19]的参数设置,以0.05 的步长将 ε设置为0.1~0.5 之间的值,以0.1 的步长将 λ设置为0.1~0.6 之间的值.DNCFS 算法涉及邻域半径参数δ,其调节范围为[0,1],步长为0.02.所有实验结果都是在最高分类准确率的情况下给出的.
3.2 实验结果
表2 给出了不同算法下所选特征的平均数.从表2 可见,KFCMI 算法大多数情况下取得了较小的特征平均数;FIE,FRFS,FDMAR 算法在一些数据集上得到的是整个属性集,这说明FIE,FRFS,FDMAR算法在一些数据集上无法有效地去除冗余特征.此外,对于平均值而言,KFCMI 算法小于FIE,FDMAR,DNCFS 算法,但略大于FRFS 和DNCFS 算法.表3~5分别展示了原始数据和基于这6 种算法的约简数据的分类准确率.
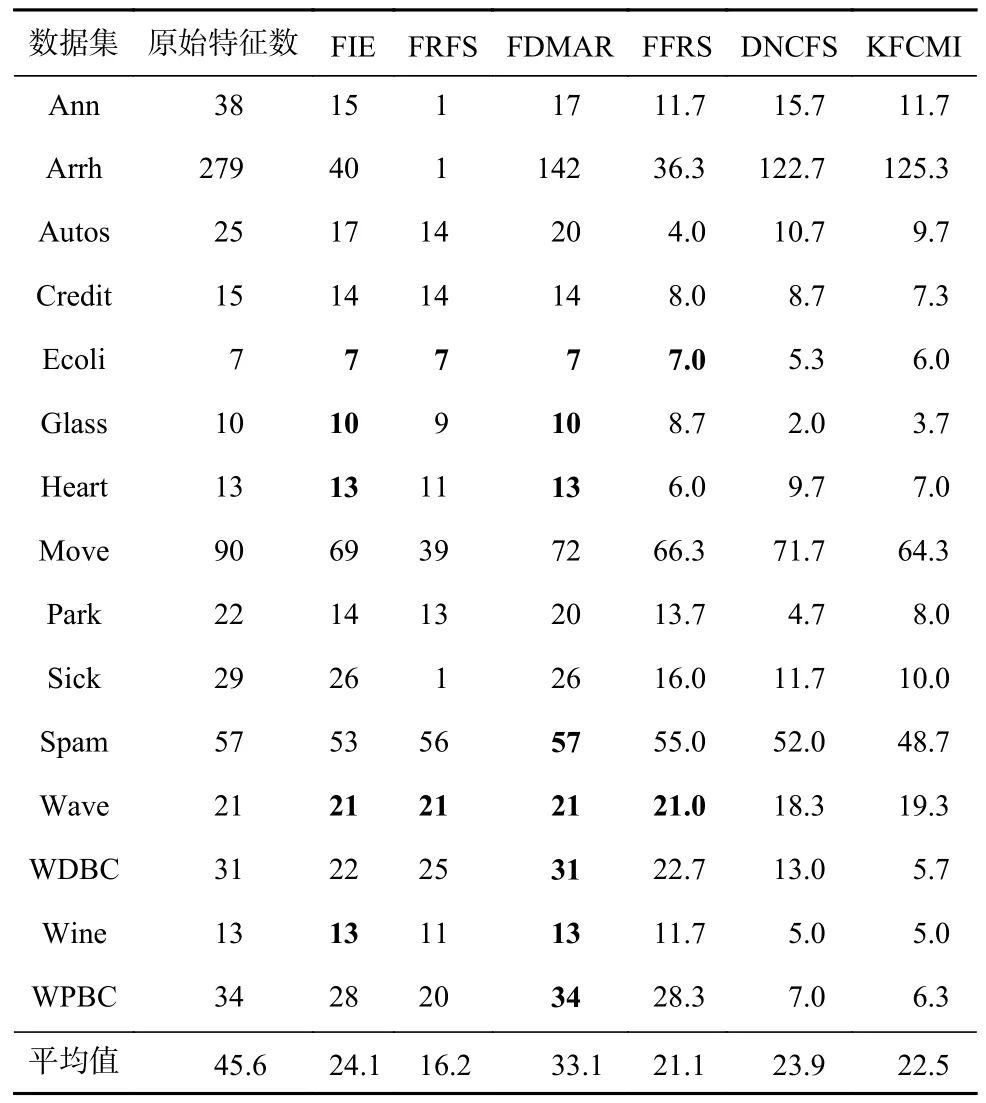
Table 2 Average Number of Features Selected by Different Algorithms表 2 不同算法所选特征的平均数
从表3~5 中可以看到,算法KFCMI 在所有数据集上都能提高或保持原始数据的分类准确率.在表3~5 中45 条记录中,KFCMI 算法有29 条记录实现了最佳分类准确率.然而,对于FIE,FRFS,FDMAR,FFRS,DNCFS 算法,分别仅有2,0,0,8,8 条记录实现了最佳分类准确率.更多的是,KFCMI 算法的平均分类准确率在3 种分类算法上均优于其他所有特征选择算法.

Table 3 Classification Accuracy of Different Algorithms Based on CART Algorithm表 3 基于CART 算法的不同算法分类准确率 %
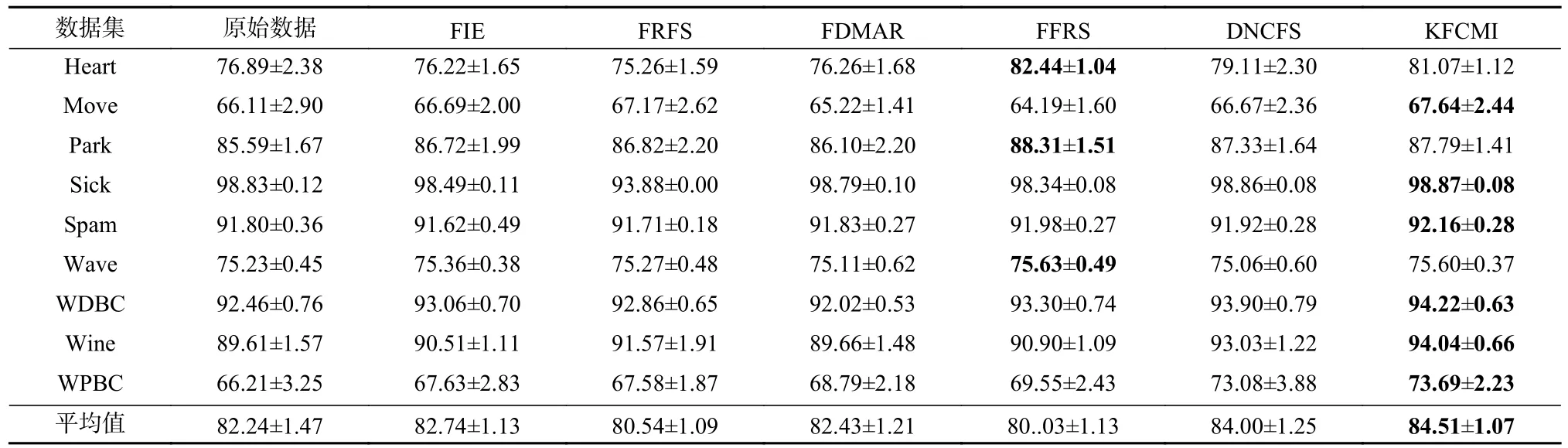
续表 3
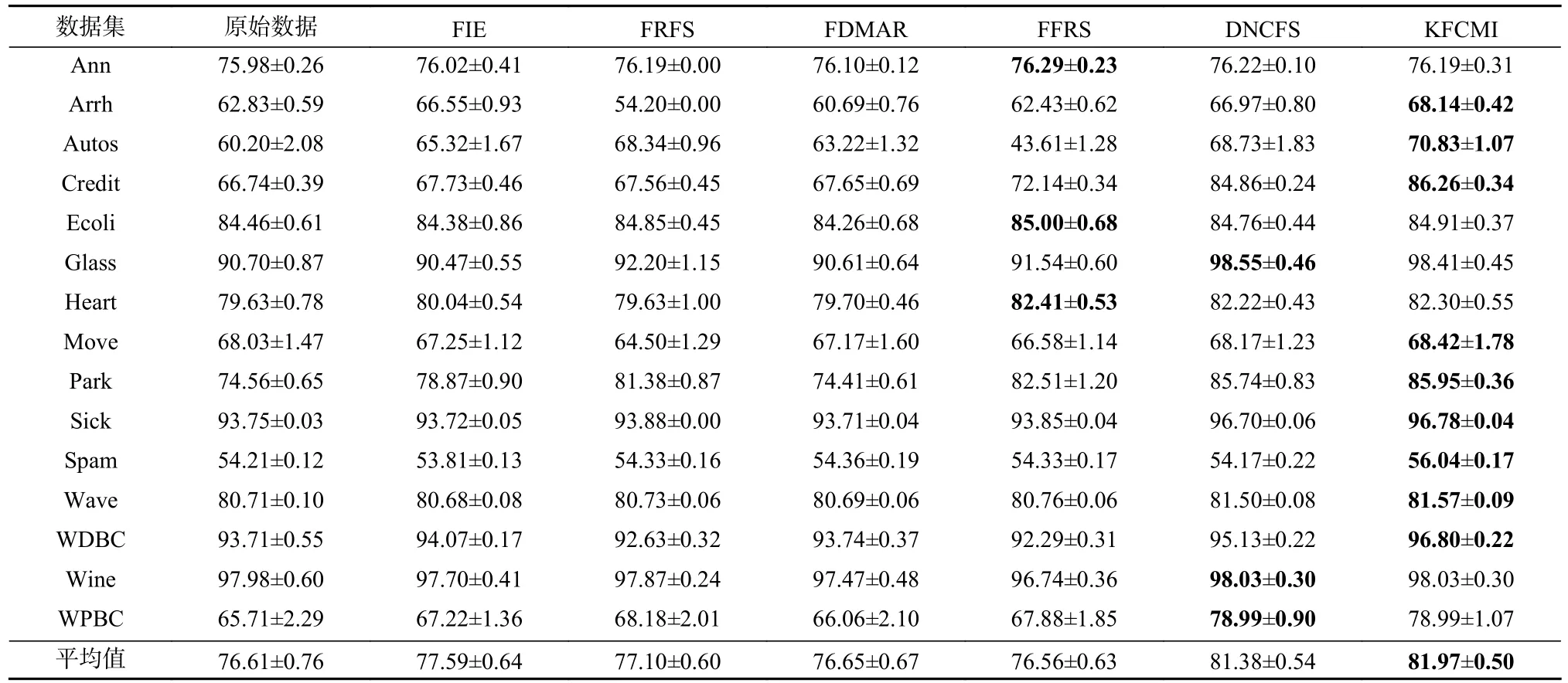
Table 4 Classification Accuracy of Different Algorithms Based on NB Algorithm表 4 基于NB 算法的不同算法分类准确率 %

Table 5 Classification Accuracy of Different Algorithms Based on kNN Algorithm表 5 基于kNN 算法的不同算法分类准确率 %
综上,KFCMI 算法实现了较优的分类准确率.KFCMI 算法可以选出相对较小的特征子集并提高或保持分类准确率.而这15 个数据集包括数值和混合属性数据集,因此,KFCMI 算法适用于多种属性类型的特征选择.
3.3 实验参数
为了分析本文所提算法KFCMI 的性能对参数的敏感性,3 种分类算法的所选特征数及分类准确率随参数的变化如图1 所示.显然,可以看到不同参数可能导致不同的特征数及分类准确率.下面从所选特征数和分类准确率2 方面来进行分析.

Fig.1 Average classification accuracy varies with parameters图 1 平均分类准确率随参数的变化
1)就特征数而言.通过图1 可以看到,在大多数数据集上,随着 σ的增加,所选特征数均呈递增的趋势,最后趋于平衡.例如,Arrh,Ecoli,Move 等数据集.然而,对于Autos,Credit,Heart 等数据集,所选特征数随着 σ的增加而增加,然后减小并开始波动,最后并未趋于平稳.
2)就分类准确率而言.从图1 可以看到大多数数据集可以在多个参数 σ值下取得最优值.对于每个数据集,可以根据图1 选择合适的 σ值来获得较优的分类准确率.此外,从3 种分类算法的分类准确率变化曲线来看,可以看到3 种分类算法获得的结果基本上一致.
通过上述分析可以看到,实验性能对参数σ具有一定的敏感性.因此,在所提的算法中调节参数是很有必要的.但是,在合适的参数值的条件下,KFCMI算法在大多数情况下也可以获得较优的结果.
综上,KFCMI 算法对于数值和混合属性分类算法的特征选择是可行且有效的.
4 结 论
本文基于混杂核函数定义了关于决策的模糊补互信息,并证明了其关于特征呈单调性变化.进而提出了基于混杂核模糊补互信息的特征选择方法,且设计了相应的启发式算法.最后,在15 个实际数据集上对所提算法与现有算法进行了实验对比分析.实验结果表明所提算法是混合特征选择的一种有效方案.在将来的工作中,可以进一步考虑特征的交互性.
作者贡献声明:袁钟负责算法思路和实验方案的提出,以及完成实验并撰写论文;陈红梅提出指导意见并修改论文;王志红负责论文实验分析;李天瑞提出指导意见并修改论文.

