改进人工电场算法在选址问题中的应用研究 *

郑宏宇，唐竟超，姚光磊，熊菊霞

（广西民族大学 数学与物理学院，广西 南宁 530006）

0 引言

随着新经济和电商平台的日益发达，物流行业的竞争也越来越激烈。现代物流配送是指商品从仓库到需求点的实体运输过程中，按照现实需求，将装卸、运输、流通和加工等功能有机地结合以满足需求点要求的过程。在将商品从制造地运输到需求地的过程中，需要建立一个中心服务站点来集中配送商品。建立中心服务站点的主要目的是将商品有效、快捷地送达需求地点，这就是物流配送中心。物流配送中心在整条物流系统中具有着承上启下的重要功能，是供给点和需求点之间相互联系的关键纽带。因此，如何科学、合理地选定建设配送中心的地点是整条物流系统分析中的核心内容，同时也是物流配送体系合理运营的基础前提。在大规模连锁经营下，物流配送中心即连锁公司建立的物资供应管理中心，按照公司总店的安排及各分公司的需求，由配送中心向各分公司统一调配物资，利用物流配送中心大规模生产和高效率的配送方式减少公司的运营成本，以便获取最高的收益。［1］由于配送中心的选址工作是一项庞大的工程，且往往受到原料配送、运输条件等诸多因素的影响，其合理的选择既可以节省建设和维护成本，也能保证物流系统高效运作。物流配送中心规模巨大，其建设与发展不但关系到周边地区，而且关系一个城市的经济发展建设以及所在地区的生态环境，［2］因而配送中心的选址设计和优化方案具有重要的研究意义。

选址问题（Location problem，LP）［3］是运筹学中经典的问题之一，一般描述为在一个具有若干供应点及若干需求点的区域内，将一定数量的需求点设置为配送中心的优化过程。［4］1964 年，Hakimi 首先提出了网络上的P-中位问题（也称P-中值问题）与P-中心问题，自此，选址理论的研究开始活跃起来。选址问题包括P-中位问题、P-中心问题和覆盖问题三个基本问题以及多种扩展问题。多配送中心选址问题（Multi-distribution center location problem，MDLP）属于P-中位选址问题，且涉及的变量及约束条件较多，属于典型的NPhard 问题［5］，以至于一些传统的方法难以解决该问题。但随着智能优化算法的兴起和多种新型启发式仿生算法在近些年被相继提出，多配送中心选址问题成为学者们的研究热点，很多国内外专家和学者都应用智能优化算法寻找选址问题的最优解。Nong［6］采用网络分析法（ANP）和优劣解距离法相结合的方法，提出了一种支持配送中心选址的集成多准则决策分析模型（Multicriteria decision making model，MCDM）。Arsalan 等人［7］基于leader-follower 模型，提出了一个双层非线性规划领域中的枚举分支切割方法，并通过实验表明了算法的有效性。Thuy 等人［8］提出了一种基于球形模糊层次分析法和组合妥协解的混合MCDM 模型，并证明了该模型的有效性。刘培德等人［9］提出了一种基于二维语言相似度的聚类分析算法，并利用该算法构建了综合物流配送中心选址问题的多属性群体决策求解框架。Li 等人［10］通过Q 学习步长和遗传算子，给出了动态步长布谷鸟算法用于求解选址问题，并通过实验证明了该算法的性能优势。

本文从实际科学工程优化问题出发，基于Anita等人提出的人工电场算法（Artificial electric field algorithm，AEFA），针对多配送中心选址模型，提出一种改进人工电场算法（Improved artificial electric field algorithm，IAEFA）并进行了理论分析。通过仿真实验，验证了改进人工电场算法的良好性能。

1 待解问题和算法描述

1.1 多配送中心选址问题

多配送中心选址问题（MDLP）指的是在某个区域内，已知有n个需求点，要从中选择m(m＜n) 个作为配送中心向其余的需求点运输货物，在满足所有需求点货物需求的前提下，最小化配送中心与其配送范围内需求点之间的运输费用。［11］

为了方便多配送中心选址模型的建立，进行如下假设：

（1） 物流配送中心的供应量总能够满足需求点的需求量，并由其配送范围内的总需求量决定；

（2） 确保每个需求点有且仅有一个为其运输货物的配送中心；

（3） 该选址模型只考虑从配送中心到需求点的费用；

（4） 配送中心与需求点之间的距离采用二维平面的欧式距离，不考虑地面高度差异和实际道路系统（如交通堵塞、车辆故障等）。

基于以上假设，建立如下模型：

约束条件为：

式（1）为目标函数；其中，Z表示总成本，即从选定的物流配送地点到该配送范围内的每个需求点的总运费；m表示物流配送中心的数量，n表示需求点的数量，Dk表示需求点的需求量，djk表示物流配送中心j到需求点k的距离。yjk是0，1 变量，当yjk取值为1 时，表示需求点k由配送中心j配送。式（2）确保每个需求点仅由一个配送中心配送。J表示由配送中心组成的集合，K表示由需求点组成的集合。式（3）中，zj为0，1 变量，当zj取值为1 时，确定需求点j为配送中心；P表示选定的配送中心的个数。式（4）确保需求点的需求量只能被选为配送中心的点供应。式（5）、式（6）为yjk和zj的定义式。［12］

1.2 人工电场算法

人工电场算法（AEFA）［13］由Anita 等人于2019 年提出，主要模拟了带电粒子在静电场中的运动，并将其演化成随机搜索最优解的过程。带电粒子在搜索空间中受到静电力的作用进行相互吸引或排斥运动，使得自身能在搜索空间中移动。为简化带电粒子的运动原理，在AEFA 算法中，仅考虑带电粒子之间的吸引力，因此带电粒子之间可以通过吸引力的作用进行相互运动，直到所有带电粒子聚到一起。

在搜索空间中，每一个带电粒子代表一个可行解，解的适应度由带电粒子的电荷量决定，带电粒子的电荷量越大，说明该带电粒子所表示的可行解越接近最优解［14］。带电粒子的运动原理如图1所示。

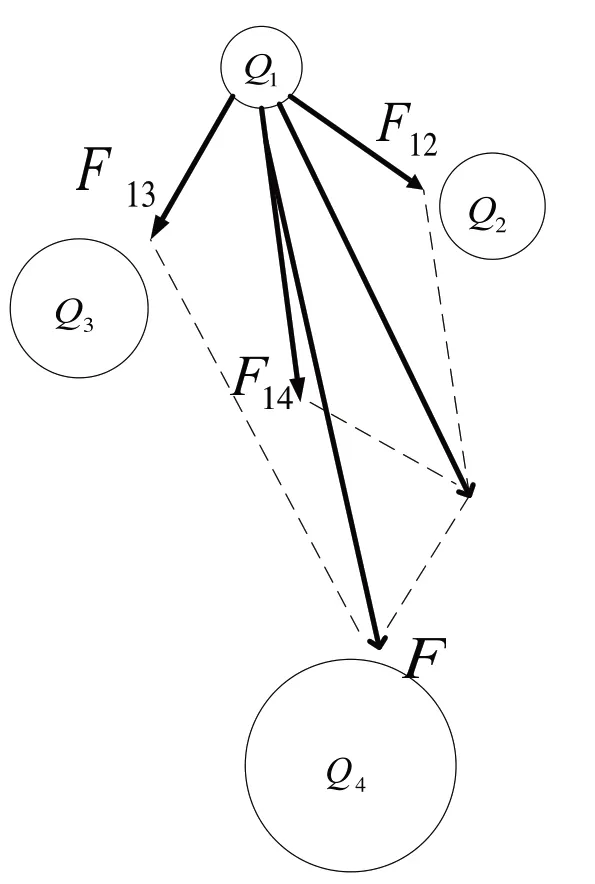
图1 带电粒子受力示意图

在图1中，每一个圆圈代表一个带电粒子，圆圈的大小表示电荷量的大小。带电粒子Q1受到其他三个带电粒子的吸引力，最终形成一个合力F和该方向上的加速度。可见Q4的电荷量最大，它对Q1的吸引力最大，所以Q1所受合力的方向更接近Q4对Q1的吸引力方向。因此，AEFA算法在进行迭代的过程中，搜索空间中小电荷粒子会向大电荷粒子移动，使算法逐步收敛到最优解。［15］

AEFA算法的数学模型可以用式（7）、式（8）来描述：

其中，rand为[0，1]之间的任意常数；Vit+1表示在第t+ 1次迭代时第i个带电粒子的速度；+1表示在第t+ 1次迭代时第i个带电粒子的位置；表示在第t次迭代时第i个带电粒子的加速度。

根据牛顿第二定律，当粒子受到电场力时，加速度的表达式为：

在第t次迭代时，带电粒子的电场强度为：

带电粒子在搜索空间中受到的合力为：

合力根据带电粒子所受库仑力计算而来，带电粒子所受库仑力模型如下：

式（12）中，Kt为库伦常数；X表示第t次迭代中的最优个体；表示在第t次迭代时，带电粒子i与带电粒子j之间的距离；ε为很小的正数。式（13）为的定义式。式（14）中，K0= 500，α= 30；iter表示当前迭代次数；T表示最大迭代次数。库伦常数的变化使得该算法在迭代前期进行全局搜索，找到最优解所在范围；在迭代后期对最优解所在范围进行局部搜索。Kt的迭代过程如图2所示。

图2 库伦常数迭代曲线

算法在迭代过程中规定第一代种群中所有粒子的电荷量均相同（设为1），从第二代开始，电荷量的迭代公式如下：

其中，表示第i个带电粒子在第t次迭代时的电荷量，为的归一化处理结果；fi为第t次迭代中第i个粒子的适应度值；best (t ) 表示第t 次迭代中的最优适应度值，worst (t ) 表示第t 次迭代中的最差适应度值。

算法在每一次迭代时的位置均由贪婪策略决定：

式（17）表示下一代个体位置的选取方式。若更新后的个体适应度劣于上一代，则个体位置不发生改变；反之采用更新后的个体作为下一代。

由上述分析可知，AEFA 算法的基本实现步骤如下：

1）在搜索空间中初始化种群数量、种群位置和最大迭代次数；

2）初始化带电粒子的速度(V= 0)、电荷量(Q=1) 和质量(m= 1)；

3）计算库伦常数，更新全局最优值和最差值；

4）更新个体速度和位置；

5）若算法达到最大迭代次数，则输出当前最优值；反之，算法跳回步骤3）。

2 人工电场算法解决MDLP 问题原理

人工电场算法的求解是以库伦定律为依据的逐代搜索过程。在实际求解时，采用随机数编码策略，设定维度D等于需求点个数，根据所需配送中心的数量对个体进行排序并取前m个编号得到所需的配送中心位置。编码和解码过程如图3 所示。

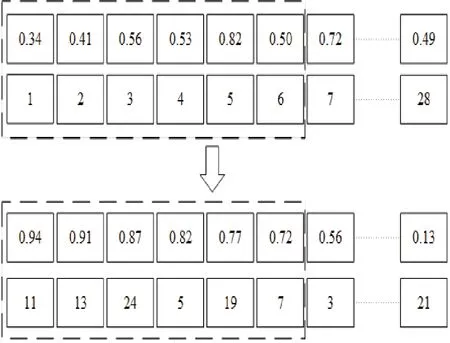
图3 编码及解码策略

假设种群数量为N，维度为28，意味着共有28 个需求点。以选取6 个配送中心为例，由图3 可知，从种群X=(X1，X2，…，XN) 中 任 意 选 取 个 体Xi，i∈{1，2，…，N}，Xi=（0.34，0.41，0.56，0.53，0.82，0.50，0.72，…，0.49）。对Xi进行排序，取前6 个的编号（11，13，24，5，19，7），该编号代表一个可行解，即选取编号为11，13，24，5，19，7 的需求点为配送中心。

3 改进人工电场算法

3.1 正余弦算法迭代机制

正余弦算法（Sine cosine algorithm，SCA）［16］利用正余弦函数的数学性质，通过添加自适应参数改变正余弦函数的振幅以实现算法的全局搜索和局部开发过程，最终寻得最优解。在SCA 算法中个体位置的更新公式如下［17］：

式（18）中，表示在第t+ 1 次迭代时第i个个体的位置；Ptbest表示第t次迭代时种群中的最优个体的位置；参数r1控制个体的搜索方向和步长在迭代时的影响程度；参数r2控制个体在迭代过程中的搜索距离；r3是一个随机权重系数，决定最优个体位置对当前个体下一次迭代的影响程度；r4是控制算法进行正弦迭代或余弦迭代的转换概率；式（19）中，a为常数（一般取2）；iter 表示当前迭代次数；T表示最大迭代次数；式（20）中，r2为(0，2π) 之间的任意常数；式（21）中，r3为(0，2) 之间的任意常数；式（22）中，r4为(0，1) 之间的任意常数。

为了更好地协调正余弦算法的全局搜索和局部开发过程，现对其进行改进。参数r1作为线性函数，不利于在算法迭代前期进行充分的全局搜索，这导致算法在后期的局部寻优能力变差。因此对参数r1进行如下调整：

与之前相比，改进后的r1使SCA 算法的全局搜索更加充分，并且利用余弦函数的数学特点，使得r1在固定的范围内上下振荡，更好地平衡了算法的全局搜索与局部开发过程。

3.2 反向学习策略

Haupt 等人［18］指出，初始种群的优劣会直接影响基于种群迭代的群智能优化算法整体的搜索速度和解的精度，多样性好的初始种群有助于提高算法的优化性能［19］。然而，原始AEFA 算法在迭代前采用随机方式初始化种群个体，这导致初始种群存在偶然性，从而在一定程度上影响了初代种群的引导效果，这会直接影响算法的收敛精度和速度。Tizhoosh 于2005 年提出的反向学习策略（Opposition - based learning，OBL）［20］，目前已被成功应用在蝗虫优化算法（GOA）、遗传算法（GA）、蚁群算法（ACO）和蝴蝶优化算法（BOA）等算法。反向学习策略中关于反向点的定义如下：［21］

假设在[lb，ub] 中存在数x，则x的反向点定义为x′=lb+ub-x。将反向点的定义扩展到D维空间，设p=(x1，x2，…，xD) 为D维空间中的一个点，其中xi∈[lbi，ubi]，i= 1，2，…，D，则其反向点

3.3 精英个体保留策略

在种群进行迭代更新时，为确保精英个体即适应度好的个体进入下一代循环，采用精英个体保留策略。［22］从第二次种群迭代开始，每次迭代结束后，均对新一代种群计算反向点。将新一代种群与其反向点进行种群合并操作，并计算适应度值，用适应度好的个体替换适应度差的个体，使得子代精英个体作为父代继续迭代。这可以在一定程度上提高算法的收敛精度。

3.4 柯西扰动策略

柯西扰动策略［23］又称柯西变异，源自柯西分布。一维柯西分布概率密度如下：

当a= 1 时，上式称为标准柯西分布。图4 为高斯分布与柯西分布的曲线对比图。

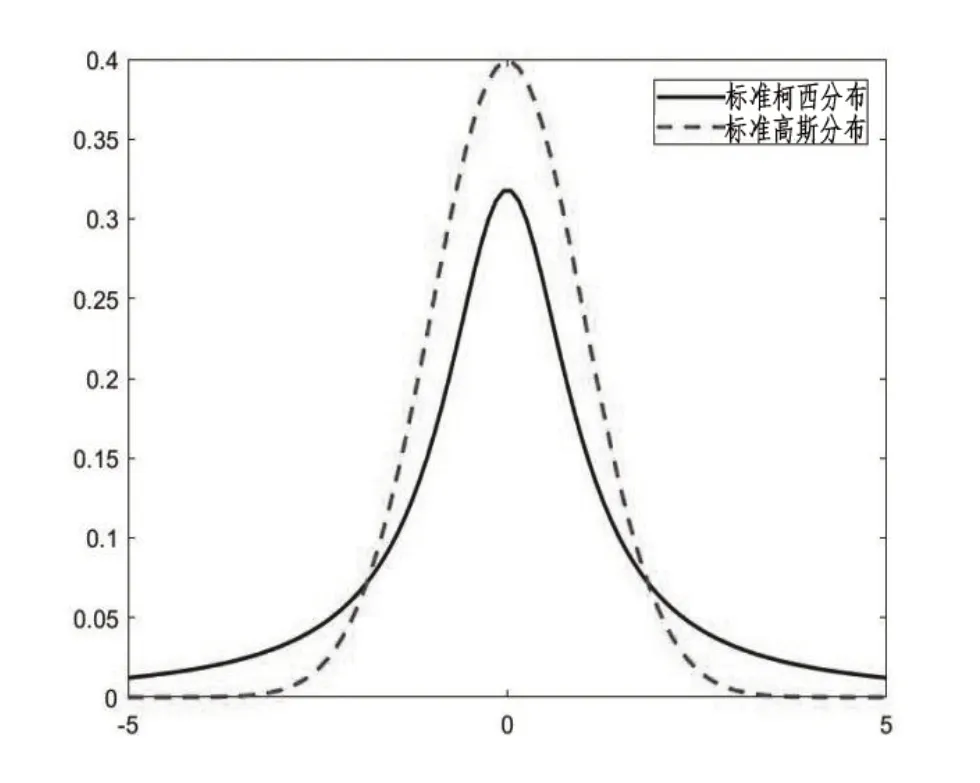
图4 两种分布的概率密度曲线对比

从图4 可以看出，柯西分布逼近于0 的过程相对平稳，比高斯分布更慢，而且在原点附近的峰值也比高斯分布更小。综上所述，柯西分布可以在计算中产生更强的扰动能力。将柯西变异引入目标位置的更新方式中，利用柯西分布产生的随机数改变当前迭代的最优值，提高算法的全局搜索能力和脱离局部最优能力。［24］

式（25）中，cauchy (0，1) 为标准柯西分布。柯西分布随机变量生成函数为

3.5 算法结构

基于上述分析，本文设计的改进人工电场算法（IAEFA）流程如图5 所示。算法步骤如下：

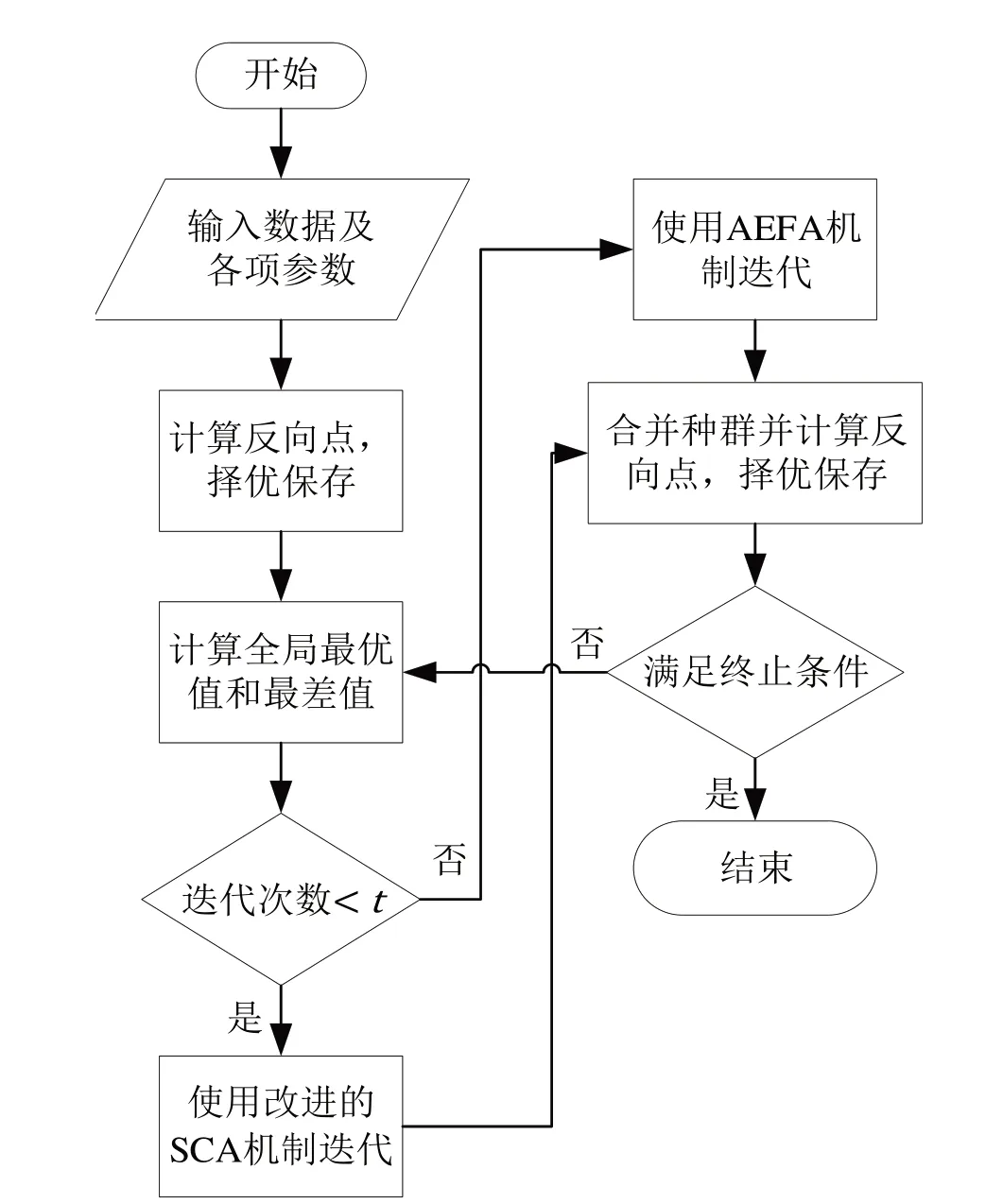
图5 算法流程图

1）初始化种群及各项参数，并计算种群反向点，择优保存；

2）计算全局最优值（柯西扰动策略）和最差值；

3）在迭代前期使用改进的SCA 迭代机制，在迭代后期使用AEFA 迭代机制；

4）获得新种群，计算反向点，使用精英个体保留策略择优保存；

5）若算法达到最大迭代次数，则输出最优解；反之，算法跳回步骤2）。

4 算例仿真和结果分析

假设在有28 个需求点的某一区域内，经决策需选取6 个需求点作为配送中心向其他需求点运输货物，表1 为每个需求点的位置及需求信息。进行算例仿真时设置人工电场算法的种群规模N= 50，最大迭代次数T= 30。使用软件：MATLAB R2018a，运行环境为64 位Windows 11 操作系统，计算机硬件参数：处理器类型为AMD Ryzen 5 3500U。机带RAM 为12.0 GB，64 位操作系统。

表1 需求点坐标及需求量

为保证实验结果的有效性，针对该MDLP 问题，将AEFA 算法和IAEFA 算法独立运行10 次，结果如表2～表3、图6～图7 所示。

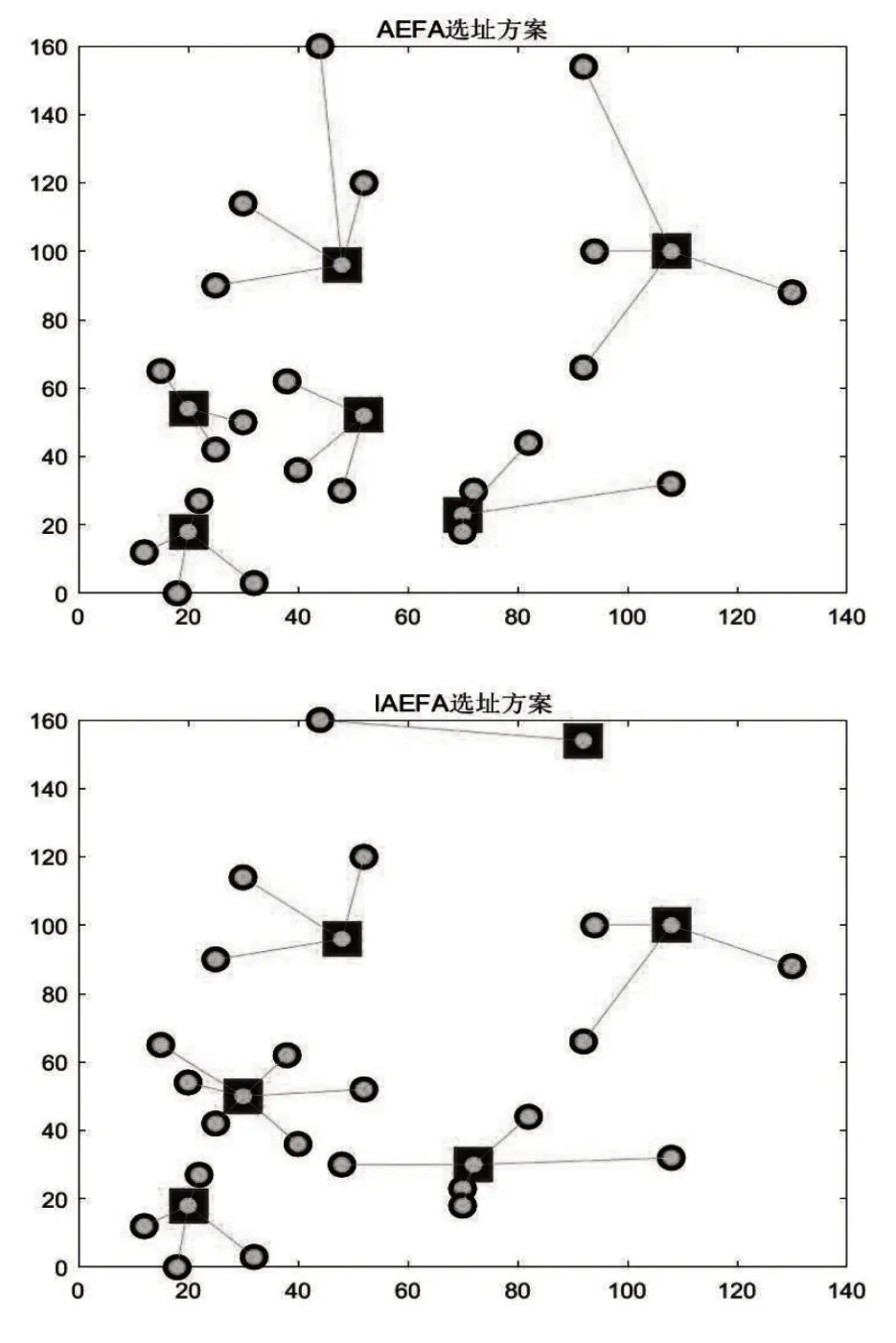
图6 选址方案对比

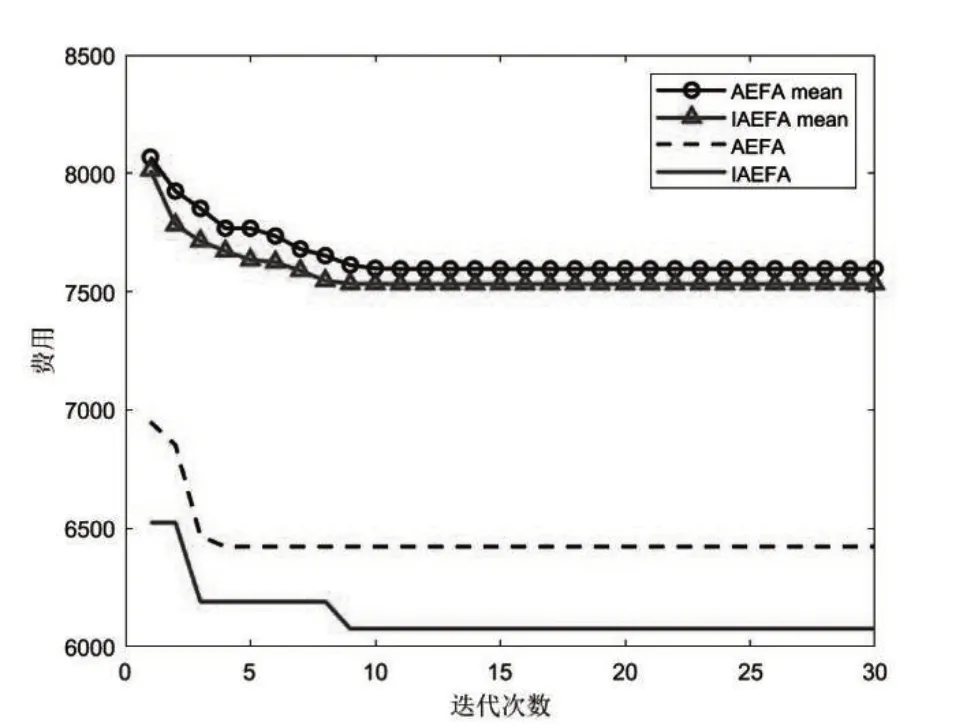
图7 寻优曲线对比

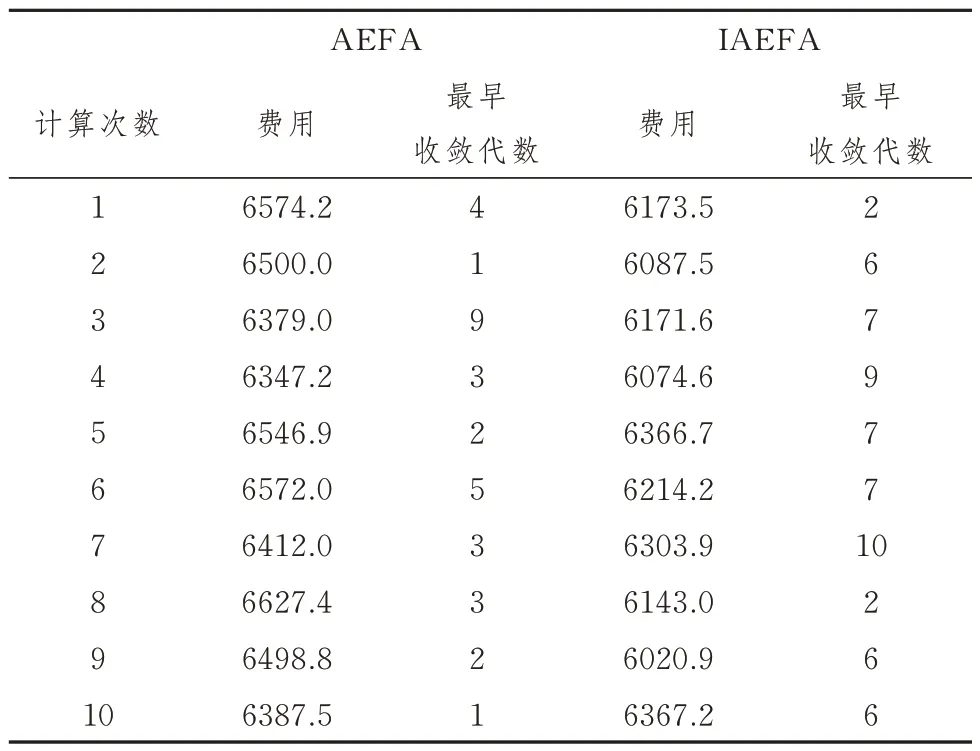
表2 AEFA 和IAEFA 实验结果对比

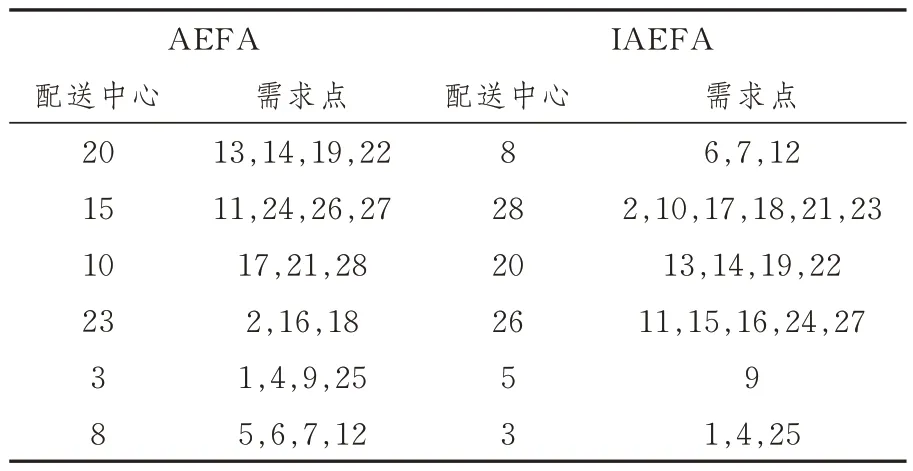
表3 选址方案及配送方案对比

由表2 可知，在10 次独立实验中，AEFA 算法的最小费用为6347.2，IAEFA 算法的最小费用为6020.9，与AEFA 相比，IAEFA 的最小费用节省了326.3。图7的寻优曲线也表明，不论是最优值还是平均值，IAEFA 算法计算结果的都比AEFA 算法的结果更小，这说明了本文算法的改进方式具有一定的性能优势。

将人工鱼群算法（AFSA）、文献［11］、人工电场算法（AEFA）和本文的改进算法（IAEFA）应用于上述MDLP 问题，四种算法的对比结果如表4 所示。

表4 性能对比

由表4 可以看出，在最优值方面，IAEFA 算法的计算结果是6020.9，比其他三种算法节约了313.1 以上；在平均值方面，IAEFA 算法的计算结果是6192.31，比其他三种算法节约了265.69 以上，说明IAEFA 算法具有更高的求解精度；在标准差方面，IAEFA 算法的结果是114.61，相比于其他三种算法具有一定的稳定性；在平均收敛代数方面，虽然IAEFA算法不是最快的，但仍然比AESA 算法和文献［11］快了3 代以上。综上所述，在解决多配送中心选址问题上，IAEFA 算法具有较高的搜索性能。

5 总结

本文针对多配送中心选址问题，提出了一种改进人工电场算法（IAEFA）。该算法在初始化种群时，利用反向学习策略，以提高初始种群规模的方式增加多样性，从而使算法的第一代种群具有更好的引导效果；在计算全局最优值时，引入柯西扰动策略，改变每次迭代时最优个体的位置，避免了算法出现过早收敛的情况；在迭代过程中，引入正余弦迭代机制以平衡算法的全局搜索和局部开发过程；在每一次迭代结束后，引入反向学习策略和精英个体保留策略，不仅提高了种群的多样性，还确保每次迭代后都是好的结果替换差的结果，大幅度提高了算法的收敛精度。通过仿真案例表明，相比于原始人工电场算法、人工鱼群算法和文献［11］中的ALMM-AFSA 算法，本文提出的IAEFA 算法在求解多配送中心选址问题时具有更好的性能。但是，由于多配送中心选址模型的建立基本处在理想情况下，因此，对于更符合真实环境，具备更高实际参考价值的选址模型是今后进一步的研究工作。除此之外，国内外对人工电场算法的改进研究仍处在初期阶段，算法性能尚未被完全发掘，仍具有较大的提升空间，因此进一步开发人工电场算法的性能优势，分析算法的性能特点是今后深入研究的另一重要方面。