基于核KMeans和SOM神经网络算法的海况聚类分析
陈晓曼, 苏 欢
(哈尔滨工业大学(威海) 理学院, 山东 威海 264209)
0 引言
海况是海洋与大气、海洋与海冰之间耦合的关键组成部分,对海上的运输、生产和海洋资源的开发使用等有着至关重要的作用[1,2].研究者们[3-6]通常使用有效波高作为海洋活动中海况的使用指标,而海况对于船舶的影响往往是多种海况参数非线性耦合的结果.Dodet等[7]表示在未来的研究中,多源数据的使用将为复杂现象提供更加完整的描述.海况数据用户在研究和工程应用中仍然主要依赖于数值波浪模型[8],为了能够更加合理且高质量地使用海况数据,考虑利用机器学习方法对海况参数进行聚类,从而得到更加全面可靠的结果.
目前国内外有一些研究通过数据挖掘对海况参数进行聚类和智能识别从而实现航速优化[9-11].王壮[12]利用KMeans算法对海况数据进行聚类,智能地根据不同海况采用最佳经济航速,实验结果表明该方法能够有效地实现航速优化.然而KMeans聚类算法对于高维非线性数据的聚类效果并不理想,故而对于实现海况参数聚类的方法也还有待改进.
在众多的聚类算法中KMeans[13]聚类算法应用最为广泛,自组织映射(Self-organizing Mapping,SOM)神经网络算法是全局排序的且被认为对于任意数据具有鲁棒性[14].为克服KMeans算法难以处理复杂数据的不足,有学者提出利用核方法将数据嵌入高维流形,将欧氏距离替换成非线性核距离来衡量相似度[15-17].因此本文基于KMeans、SOM神经网络算法、核技巧,构建了自组织映射混合核KMeans(SOM-Gaussian and Polynomial Kernel-KMeans,SGPK-Kmeans)算法.针对单核KMeans无法全面准确地反映数据内在联系的问题,将高斯核函数与多项式核函数进行线性组合,得到兼顾学习能力和泛化能力的混合核KMeans来更合理的描述数据的内部联系从而提升聚类效果;由SOM神经网络算法确定混合核KMeans的初始聚类中心以及聚类数目,可以有效避免随机选择初始聚类中心导致的聚类效果不稳定以及易陷入局部最优的问题.
本文构建了SGPK-KMeans聚类算法,使用夏威夷群岛北部的浮标,以1小时为分辨率选取从2021年1月到12月的数据共8 588组进行海况参数的聚类分析,并综合考虑SC(Silhouette Coefficient)分数、CH(Calinski Harabaz)分数以及DBI(Davies Bouldin Index)指数对聚类的效果进行评估.实验表明,使用SGPK-KMeans算法对数据进行聚类所得到的聚类评估效果最好,从而本文构建的算法可以为海况的智能识别、航速优化提供更加全面准确的聚类结果,也可以为其他受海况影响的应用提供更加可靠的海况聚类结果.
1 预备知识
1.1 KMeans算法
KMeans是一种基于划分的聚类算法,旨在最小化数据点和聚类中心之间的平均平方距离[18].该聚类方法的思想可以归结为对样本集合X={x1,x2,…,xn}的划分,xi(i=1,2,…,n)表示数据集中第i个样本数据.通常使用欧氏距离作为距离度量.但该方法在复杂和未知形状组织的数据中表现得并不理想[19].KMeans通过最小化损失函数:
(1)
1.2 核函数
定义1[20]设χ是输入空间,H是特征空间,若存在映射φ(y):χ→H使得对于任意y,z,∈χ,函数κ(y,z)满足κ(y,z)=φ(y)·φ(z),则称κ(y,z)为核函数,φ(y)为映射函数,式中·表示内积运算.
定义2[21]令χ为输入空间,κ(·,·)是定义在χ×χ上的对称函数,若κ是核函数,对于任意数据x=(x1,x2,…,xm),称矩阵:
为核矩阵.由文献[20]知,只要一个对称函数对应的核矩阵半正定,该函数就可以作为核函数使用.常用的核函数有多项式核函数:
κ(y,z)=(βy·z+γ)p
(2)
高斯核函数:
(3)
定理1假设κ1,κ2是核函数,λ∈(0,1),那么λκ1+(1-λκ2)也是核函数.
证明:由κ1,κ2均为核函数,知κ1,κ2均为对称函数且生成的核矩阵K1,K2半正定,则
κ(xi,xj)=λκ1(xi,xj)+(1-λ)κ2(xi,xj)=λκ1(xj,xi)+(1-λ)κ2(xj,xi)=κ(xj,xi)
即κ(xi,xj)是对称函数,下证该对称函数对应的矩阵K半正定.
由于K=λK1+(1-λ)K2,其中K1,K2半正定且λ∈(0,1),故对称函数κ对应的矩阵K半正定,从而由定理知该函数是核函数.
若核函数选取不当,会将输入空间映射到不恰当的特征空间使得聚类效果不佳.高斯核函数学习能力较强泛化能力较弱;多项式核函数学习能力较弱泛化能力较强.基于此,考虑将高斯核函数与多项式核函数相结合,使用这两种核函数的线性组合生成新的核函数构造核矩阵,能够同时保证算法的学习能力和泛化能力,从而提升聚类效果.本文构造的核函数为:
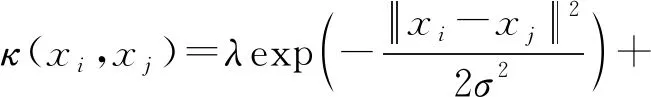
(4)
式(4)中:λ∈(0,1).
1.3 SOM神经网络算法
SOM神经网络算法是芬兰的Kohonen教授[22]提出的一种由全连接的神经元列阵组成的神经网络理论,神经网络的输入层和竞争层之间通过权重向量实现全连接.能够根据输入空间中数据集的概率分布密度形成与此概率密度相对应的输出的分布关系[23].在学习过程中,竞争层的神经元节点通过相互的侧向交互作用竞争成为与输入神经元节点最相似的那个节点,相似度最高的节点为获胜神经元.获胜神经元会根据权重调整公式进行更新调整,周围的神经元也会受到其影响调整权重,故而SOM神经网络算法在实现聚类的同时保持了输入空间的拓扑结构.SOM神经网络通过大量神经元同时作用,容错性好、鲁棒性强,但是网络结构比较固定,可能会出现“死神经元”.SOM神经网络拓扑结构如图1所示.
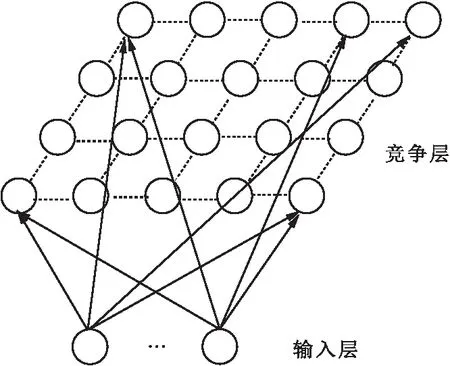
图1 SOM神经网络拓扑结构图
2 SGPK-KMeans算法
2.1 核KMeans算法
KMeans聚类算法能够很好的确定线性聚类边界,但当簇间的边界为非线性的复杂形状时,该聚类算法不能很好地发挥作用.因此,引入非线性变换,将数据集映射到高维特征空间,在高维特征空间利用KMeans聚类,便能得到更好的聚类结果.通过核函数,隐式地实现了从低维到高维的映射,巧妙地避开了非线性映射φ的显式选取.核KMeans算法以核距离:
(5)
取代原本的欧氏距离,其中xi,xj是输入的第i,j个样本数据,κ(·,·)是核函数.相应的要求解的最优化问题转换为:
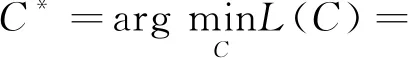
(6)
其中φ是非线性映射,满足:
κ(xi,xj)=<φ(xi),φ(xj)>.
(7)
核KMeans算法克服了KMeans算法只能处理超球形数据的不足,但是该算法仍然需要事先确定聚类数目且对于初始聚类中心十分敏感,随机选取的初始聚类中心有可能使得KMeans算法陷入局部最优.
2.2 SGPK-KMeans算法
将SOM神经网络算法引入核KMeans,由SOM神经网络算法确定初始聚类中心和k值,从而克服核KMeans不能确定聚类数目和初始聚类中心选取不当的不足.对于k值的确定,综合考虑了三种聚类内部评价指标:SC分数、CH分数以及DBI指数.
SC分数为:
(8)
式(8)中:a(i)表示向量i到它所属簇中所有其他点的距离的均值,b(i)表示向量i到它不属于的簇中所有点的平均距离的最小值,聚类结果总的SC分数是将所有点的SC分数求平均.由公式可知当SC分数越接近1说明聚类效果越好.
CH分数为:
(9)
式(9)中:h为簇的数目,N为输入空间中样本的个数,Bh为簇间色散矩阵,Wh为簇内色散矩阵,Bh,Wh公式如下:
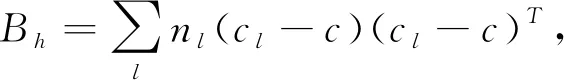
(10)
式(10)中:Cl为簇l中点集,nl为簇l中的点数,cl为簇l的中心,c为E的中心,x为cl中的数据.由公式可知若簇内数据的协方差越小,簇间的协方差越大,则CH分数越大,说明聚类效果好.即聚类结果中同类别的样本距离近,不同类别的样本之间距离远.
DBI指数为:
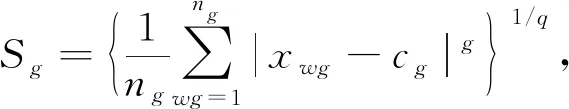
(11)
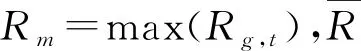
2.3 算法实现流程
SGPK-KMeans算法具体实现如下:
(1)对于输入空间数据X={x1,x2,…,xn}使用SOM神经网络算法,依据肘部法综合考虑三种聚类评价内部指标:SC分数、CH分数以及DBI指数确定聚类数目和初始聚类中心.
(2)根据第(1)步得到的结果,初始化核KMeans算法的聚类数目h及初始聚类中心c1,c2,…,ch.
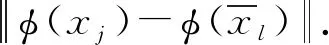
(4)将xj,j=1,2,…,n划分到与之距离最小的聚类心所属的类别中,计算每一个类别中所有数据点的均值作为新的聚类中心,不断更新聚类中心及每个类.
SGPK-KMeans算法实现流程如图2所示.
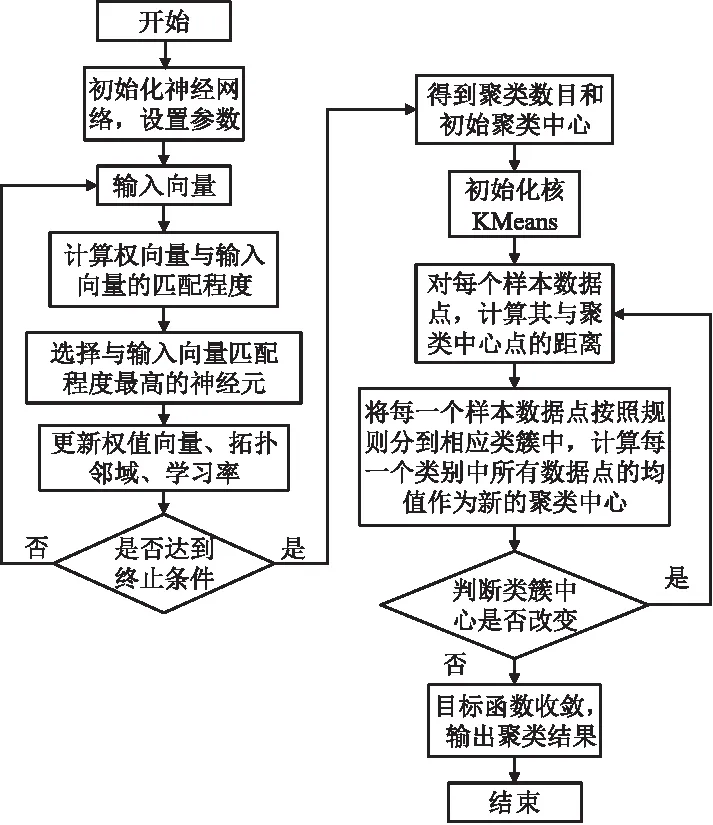
图2 SGPK-KMeans聚类流程图
3 海况聚类实验及结果分析
3.1 实验描述及数据预处理
为了实现海况的聚类并验证提出算法的有效性,本文采取来自美国国家资料浮标中心的夏威夷群岛北部地理位置(23.528 N,153.792 W)的浮标从2021年1月到2021年12月共8 588组数据(以1小时为时间分辨率)进行聚类(部分数据如表1所示).该数据集有八个特征,分别为:风向、风速、波高、阵风、大气压力、空气温度、水温、露点温度.由于特征量纲不同,在进行聚类前需要先对数据进行无量纲化,本文采用的无量纲化处理是Z-Score标准化.具体过程通过Python实现.
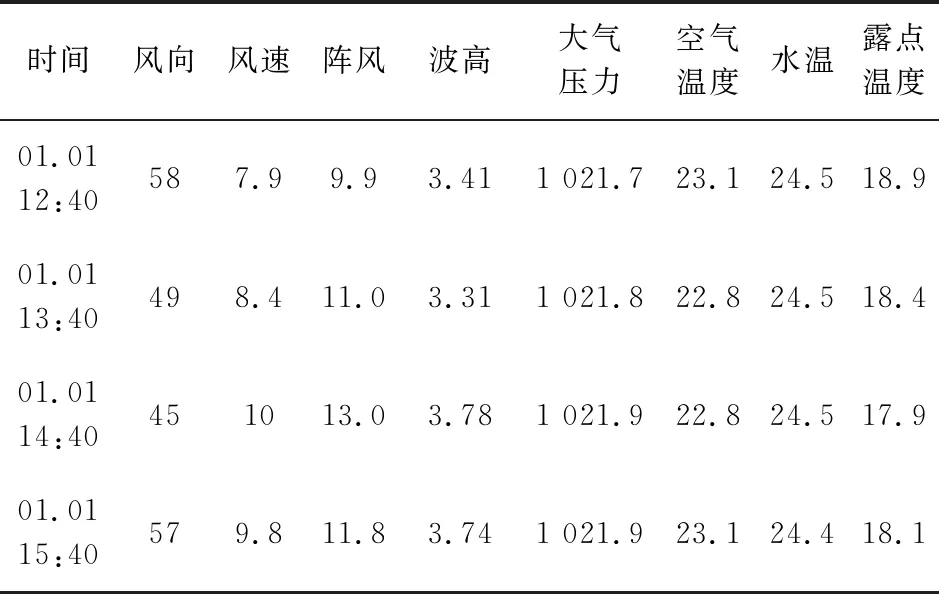
表1 部分实验数据
3.2 SOM神经网络聚类
利用SOM神经网络算法,综合考虑CH分数、SC分数以及DBI指数,得到聚类数目以及聚类中心,其中聚类数目确定为12.三种评估指标部分结果如表2所示,折线图如图3、图4所示.
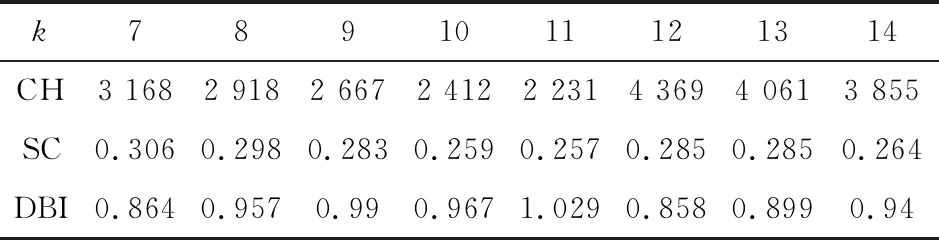
表2 SOM算法得到的部分评估指标结果
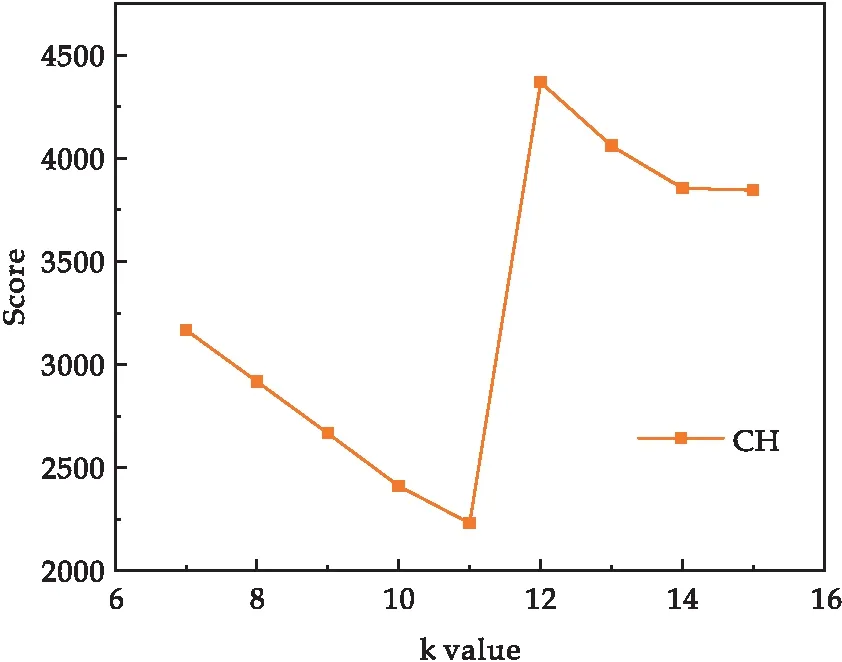
图3 CH分数评估指标结果
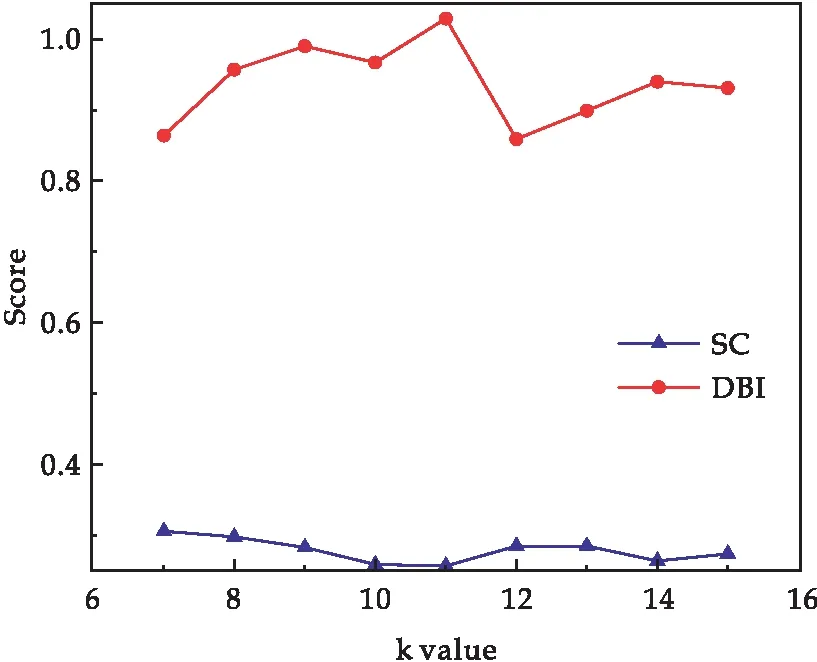
图4 SC分数及DBI指标评估结果折线图
根据确定聚类数目的拐点检测原理,本文利用机器学习中投票法的思想认为当两个指标同时达到拐点且第三个指标值处于所有该值的均值以上水平时,选择此时的k值作为聚类数目,相应的聚类中心为初始聚类中心.由表2及图3、4知,CH分数、DBI指数在k取12时达到拐点且SC分数的值高于所有SC分数的均值,故可确定聚类数目为12.
3.3 核KMeans聚类
分别利用传统KMeans算法、高斯核KMeans算法、多项式核KMeans算法、混合核KMeans算法以及SGPK-KMeans算法进行聚类,并将五种方法以及SOM神经网络得到聚类结果的SC分数、CH分数以及DBI指数进行对比.其中由于KMeans和混合核KMeans初始聚类中心是随机选取的,为避免偶然性,取七次评估平均值作为最终评估结果.表3是七次KMeans聚类评估结果,表4是七次高斯核聚类评估结果,表5是七次多项式核聚类评估结果,表6是混合核KMeans七次聚类评估结果,表7是6种不同聚类算法三个评估指标的比较结果,表8、表9分别是使用KMeans算法和SGPK-KMeans算法得到的各聚类类别数目.
3.4 结果分析
由表7可知,对于本文所用数据,高斯核KMeans聚类效果差于经典的KMeans算法和SOM神经网络算法,说明样本被映射到了不合适的特征空间.多项式核KMeans比经典KMeans聚类算法和SOM神经网络算法以及高斯核KMeans相比都有了很大改善,说明多项式核函数映射得到的特征空间是合理的,能够提升聚类效果.兼顾了学习能力和泛化能力的混合核KMeans的CH分数相比于多项式核函数提升了1.56%,DBI指数效果改善了6.02%,SC分数没有提升但相差很小,说明该核函数的设计是合理的,聚类效果有所提升.本文提出的SGPK-KMeans的聚类效果是这六种方法中最好的,三种指标均优于前五种方法,其中CH分数比传统KMeans方法提升了一倍左右,比经典SOM神经网络算法提升了1.57%,比混合核KMeans提升了0.53%;SC分数比传统KMeans提升了8.09%,比经典SOM神经网络算法提升了17.19%,比混合核KMeans提升了5.03%;DBI指数比传统KMeans改善了9.92%,比经典SOM神经网络算法改善了2.68%,比混合核KMeans改善了2.79%,因此本文提出的方法是有效且合理的.

表3 KMeans七次聚类评估结果

表4 高斯核KMeans七次聚类评估结果

表5 多项式核KMeans七次聚类评估结果

表6 混合核KMeans七次聚类评估结果

表7 6种算法聚类评估指标对比

表8 KMeans得到的各类别样本数目

表9 SGPK-KMeans得到的各类别样本数目
由表8、表9分别得到了使用KMeans和SGPK-KMeans聚类得到的每个类别样本的数目,通过观察表9发现其中类别1、类别2、类别3以及类别9的样本数目较少,返回到原数据发现类别1中数据空气温度特征和露点温度特征数据存在异常;类别2中数据的三个特征:风速、风向、阵风存在异常;类别3中波高特征数据存在异常;类别9中水温特征数据存在异常,其余类别中数据均无异常.对比KMeans聚类得到的结果,发现KMeans算法不能有效的识别出异常值,聚类效果要差于SGPK-KMeans.一方面,这说明了SGPK-KMeans聚类的有效性以及准确性,能够将某一个特征或者某几个特征有异常的数据聚在一起;另一方面,也为海况的识别提供了更多的背景情况.因此聚类得到的12个类别中有4类相当于对有异常值的数据进行了聚类,其余的8类为正常数据的海况聚类结果,即利用海洋的风速、波高等数据,应用本文提出的聚类方法,将海况分成了8类.
结合以上的实验和分析可以得出结论:SGPK-KMeans算法在聚类效果和异常值检测方面可以得到更加优化的结果,能够有效的应用于海况数据的聚类中,满足实际应用的需要.
4 结论
本文构造的SGPK-KMeans算法的聚类性能确实优于高斯核KMeans以及多项式核KMeans且显著优于传统KMeans聚类算法以及经典SOM神经网络算法.SGPK-KMeans算法对于海况数据的聚类结果更加稳定,而且还能有效的识别出数据中的异常值.应用所提聚类方法于海况聚类中,利用海面数据,将无异常值的真实海况聚成了8类,可以为海况的智能识别、异常值检测以及航速优化等提供更加全面准确的聚类效果.

