基于TentSSA-BPNN模型的钢铁企业能耗预测研究

孙健平,侯 珂,常 静

(西安石油大学 经济管理学院,陕西 西安 710065)

0 引言

第一次工业革命以来,人们通过开展大规模的工业活动显著提高了物质生活水平。电力在当今社会被认为是推动经济增长的最基本因素之一,我国国民经济的快速发展也伴随着电力需求量的迅速增加。为了确保经济平稳运行,对电能消耗进行科学有效的预测变得非常紧迫和重要。

在能耗预测方面,由于影响能耗的因素有很多,多个因素对能耗的影响可能存在着非线性的关系,故使用传统的预测方法在处理复杂问题和大量甚至海量数据时将会存在不足与缺陷。目前,有关能耗预测的相关研究中多采用线性回归、支持向量机和神经网络等方法[1]。线性回归方法建模速度快,不需要太过复杂的计算,但在处理非线性数据时陷入了困难。支持向量机的理论较为成熟,可将数据映射到高维空间,但对大规模训练样本难以应用[2]。与上述方法相比,神经网络则不存在类似的问题,在处理非线性的复杂问题时体现出了较强优势,近年来大量学者将其应用到预测研究领域。

在众多神经网络模型中,BP神经网络以其强大的非线性问题处理能力,得到了广泛应用。但是运用传统的BP神经网络进行预测时,因其自身存在的收敛速度慢、易陷入局部最优等不足,预测精度容易产生偏差。为了能准确有效地对钢铁企业的能耗进行预测,本文对传统的BP神经网络进行了改进,引入改进后的麻雀搜索算法优化BP神经网络并设计钢铁企业电力能耗预测模型,从而为企业提升能源有效利用率、制定节能政策提供一定的参考。

1 BP神经网络

反向传播神经网络(Back Propagation Neural Network,BPNN)是一种误差反向传播的神经网络模型,以其优良的预测效果,在当前研究领域得到广泛应用。其基础模型由3层结构组成,分别为输入层、隐含层和输出层。由输入层输入的数据将通过隐含层并进行处理,处理后的数据将会被输出到输出层进行误差的对比。BPNN的预测值与实际数据值的差值称为误差,若误差不满足提前设定的最小误差要求,就会将数据返回,重新传递到输入层,并在此循环的过程中调整隐含层的权重和阈值以期获得更合适的参数值,继续不断进行循环,直到达到目标的最高精度,网络循环停止。通过上述过程,BPNN的预测值逐渐与实际数据值趋近,最终达到目标。

BP神经网络凭借简单易操作、在理论和性能方面较为成熟、预测的准确度良好等特点已成为常用的神经网络模型之一。该网络的简要结构如图1所示,具体的算法公式详情介绍可参考文献[11]。

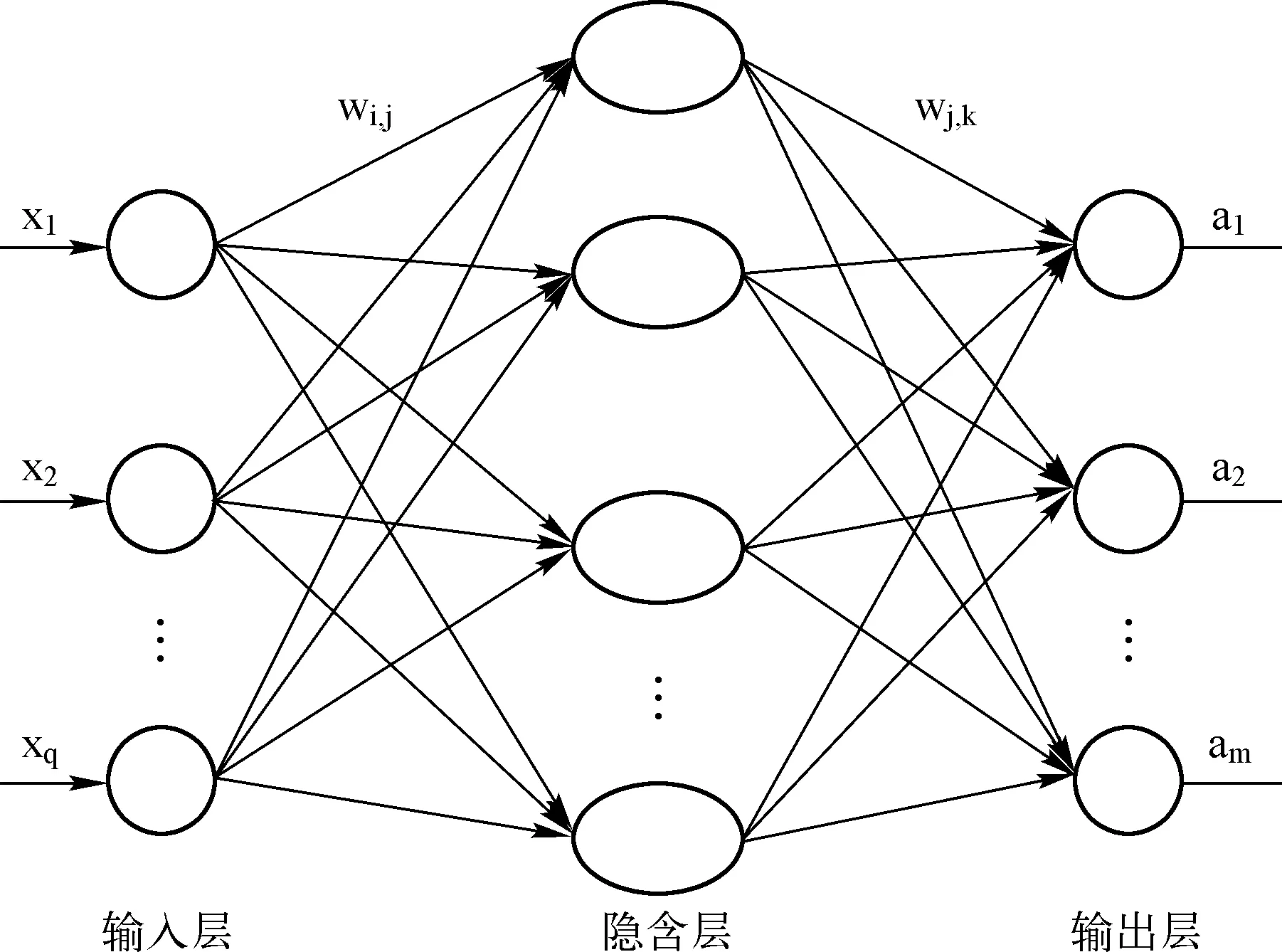
图1 BP神经网络基础结构

2 改进的麻雀搜索算法

2.1 麻雀搜索算法

麻雀搜索算法是Xue在2020年通过模拟麻雀的搜索食物行为设计并提出的一种新型智能算法[12]。在该算法中,将麻雀种群分为了探索者、跟随者和侦察者。探索者和跟随者为动态变化,比例保持不变,此外,会有10%～20%的麻雀负责警戒,被称为侦察者。

探索者的位置更新公式如下：

(1)

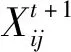
跟随者位置的更新方式如下：

(2)

式中,Xworst为全局最差位置;Xp为全局最佳位置;A代表一个1×d的矩阵,其元素随机赋值为-1或1;且A+=AT×(AAT)-1。

侦察者会观察周围环境,一旦察觉到危险,就会发出信号,探索者和追随者都将放弃食物,开始反捕食行为。侦察者的位置更新方式如下：

(3)

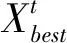
2.2 Tent混沌映射优化SSA

麻雀搜索算法与目前大多数的种群搜索算法一样,都是以随机初始种群开始寻优,比如粒子群算法(PSO)、灰狼算法(GWO)、蝙蝠算法(BA)、差分进化算法(DE)、鲸鱼优化算法(WOA)。在这类算法的执行过程中,随机生成的初始种群会破坏种群的多样性,即存在种群分布不均匀的问题,造成搜索空间不足进而影响最终的搜索结果。

混沌映射是一种常用的初始种群优化方法,它具有随机性、遍历性和规律性的特点[13],能够让种群保持多样性,因此该方法被广泛的应用于算法优化研究[14]。目前常用的混沌模型有Tent混沌映射、Logistic混沌映射等,其中Tent混沌映射已经被证明在均匀分布以及收敛速度方面要优于Logistic混沌映射[15],因此本文选择将Tent混沌映射函数引入到传统的麻雀搜索算法当中,形成了TentSSA算法。

TentSSA算法优化了初始的麻雀种群,得到了分布更加均匀的初始麻雀个体。本文所使用的Tent混沌映射函数如下：

(4)

式中,β∈(0,1);Zk∈[0,1],k=1,2,…,d。

3 TentSSA-BPNN预测模型

传统的BP神经网络采用了梯度下降的方法处理网络参数,收敛速度较慢,而且无法保证找到误差函数的最小值,存在得不到全局最优值,容易陷入局部最优的缺点。BP神经网络对初始权重和阈值、学习率等参数较为敏感,网络的调节能力较差,对于网络的初始权重和阈值,该模型采取的是随机生成的方式,训练的结果存在着较大的不确定性。由此可见,确定出最优的BPNN所要设定的初始权重与阈值对提高模型预测精度至关重要。为避免网络模型陷入局部最优,提高对于权重和阈值的寻优能力,本文采用TentSSA算法对传统的BPNN模型进行优化,TentSSA算法拥有着较高的收敛速度和较强的搜索能力,对BP神经网络的最优初始权重与阈值的搜索性能有了明显提升。

最终构建的TentSSA-BPNN的模型的工作流程图如图2所示。

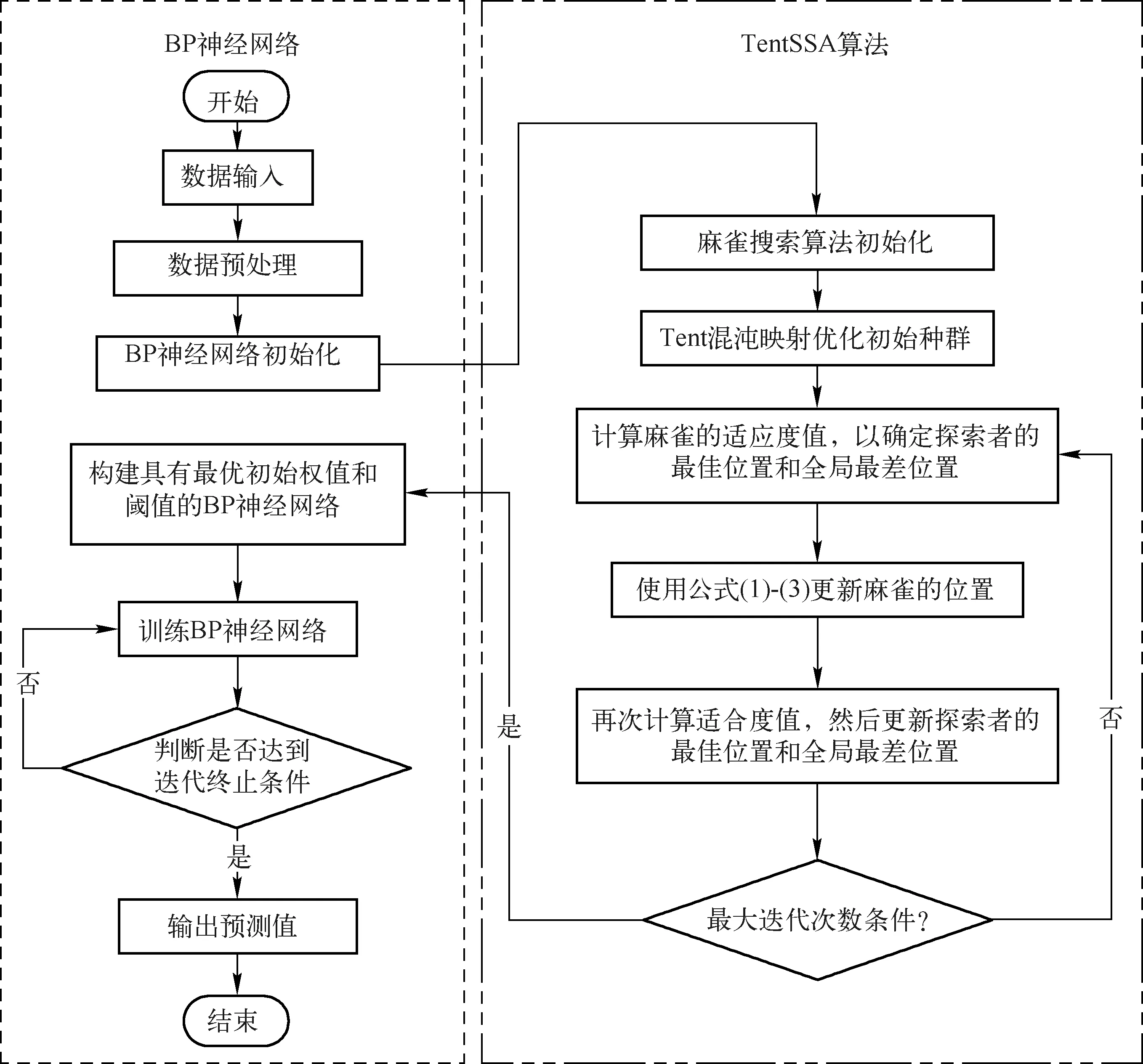
图2 TentSSA-BPNN能耗预测模型工作流程图

模型的主要工作步骤如下：

步骤1：预处理、归一化输入数据,根据3：1的比例划分训练集和测试集,按照预先设定的参数确定出BP神经网络的结构,并生成权重和阈值等相关参数。

步骤2：初始化麻雀算法。设置麻雀种群的数量、最大迭代次数、报警阈值等参数。

步骤3：利用公式(4)中的Tent混沌映射函数优化初始麻雀个体位置。

步骤4：计算麻雀的适应度值,确定最优和最差值,以及最优位置和最差位置。

步骤5：利用公式(1)-(3)更新麻雀的位置。

步骤6：计算种群个体的适应度值。并再次更新探索者的最优与最差适应度值,以及最佳个体位置和最差个体位置。

步骤7：反复步骤5-步骤6,判断是否超过迭代次数限制,若超过,则将得到的最优权重、阈值赋给BP神经网络;否则转入步骤4继续运行。

步骤8：训练BP神经网络。将训练的输出结果与训练数据的实际值进行对比并计算误差,不断循环迭代,直到达到次数限制或精度要求后终止训练过程,得到最优的BP神经网络。

步骤9：将测试数据输入到优化后的BPNN模型中进行预测,得到预测值。

4 工程实例应用

4.1 工程背景

能源的消耗随着经济增长和技术进步而逐渐扩大,在双碳目标下,钢铁企业这一巨大的能源消耗源头,如何提高降低能耗成本,实现节能减排,成为企业首先要解决的关键问题。本文以钢铁企业的能源消耗预测为研究问题,展开了分析研究。

选取某钢铁企业的电力能耗数据,测量指标包括：滞后电流无功功率、超前电流无功功率、滞后电流功率因数、超前电流功率因数、二氧化碳排放、负载类型。数据来自UCI数据库[16],利用本文提出的TentSSA-BPNN模型对该钢铁企业电力能耗进行预测,部分数据结构和样例见表1。

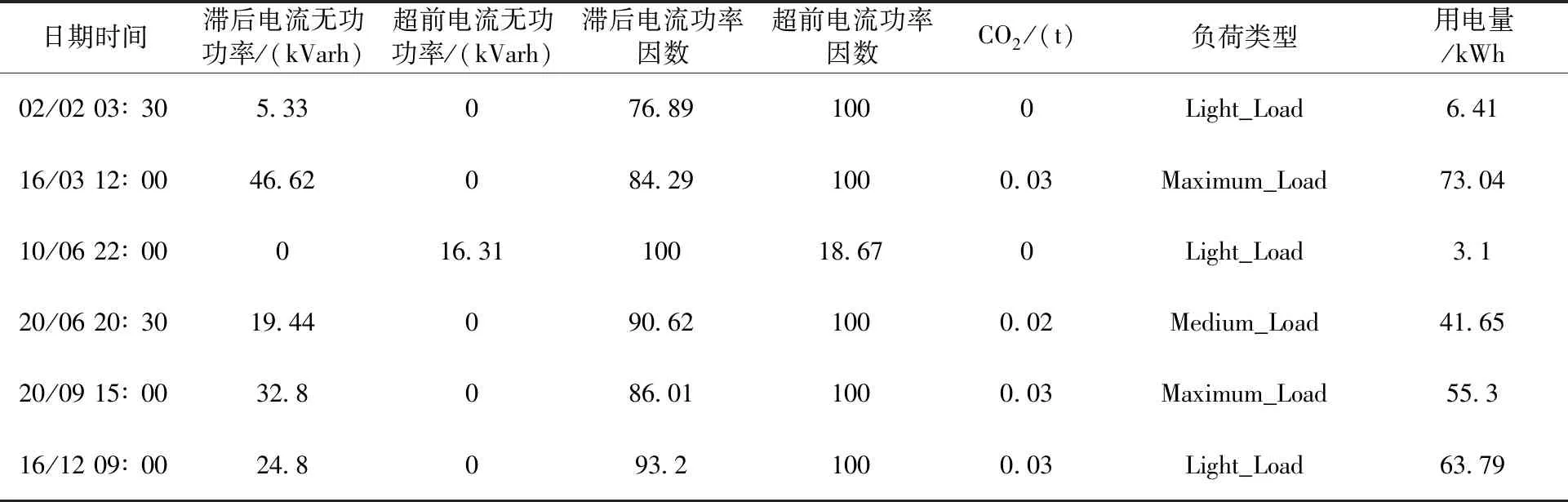
表1 钢铁企业能耗的部分相关指标数据

4.2 仿真实验与分析

利用本文提出的TentSSA-BPNN模型对收集到的数据进行预测,并使用传统的SSA-BPNN模型、BPNN模型作为对照组,验证所提出算法模型的优势。

(1) 数据处理

出于实验的效率成本考虑,本次实验从UCI数据库的35040条数据中筛选出了8064条数据。选择依据是,选定了每月前28天中的偶数日纳入采样范围,其中每条数据的时间间隔为30分钟,实验开始之前需要将实验数据归一化,其中负载类型这一影响变量在归一化之前需要转换为1、2、3,对应关系为,低负载为1,中负载为2,高负载为3。

实验数据划分为两类：a)训练样本6048条数据,用于TentSSA-BPNN模型的训练;b)测试样本2016条数据,用于检验TentSSA-BPNN模型的预测效果。

(2) 实验参数设置

为保证算法的公平性,本实验将SSA和TentSSA的初始种群规模设为相同值,麻雀搜索算法的最大迭代次数、预警值等参数见表2。

表2 基础麻雀算法参数设置

BPNN模型输入、输出层神经元数量、经过测试后确定的隐含层神经元数量、训练目标最小误差等参数见表3。

表3 基础BPNN参数设置

(3) 误差分析

为了验证TentSSA-BPNN模型的预测效果,将传统BPNN模型、SSA-BPNN模型设为对照组,与TentSSA-BPNN模型一起用于对钢铁企业电力能耗数据的预测,最后,得到这些神经网络模型的能耗预测值与实际值的对比结果。本文采用均方误差(Mean Squared Error,MSE)、平均绝对误差(Mean Absolute Error,MAE)、平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)三个误差指标来衡量预测值与实际值的差异情况,误差指标的公式如下。

(5)

(6)

(7)

表4为BPNN预测模型、SSA-BPNN预测模型、TentSSA-BPNN预测模型对钢铁企业电力能耗进行预测时,得到的能耗预测值与实际值之间的MSE、MAE和MAPE。由表4可以明显看出,采用TentSSA-BPNN预测模型进行企业能耗预测所得到的MSE、MAE和MAPE比另外两种模型更小。其中,与BPNN相比较,分别下降了76.69%、49.58%和47.49%,与SSA-BPNN对比,分别下降了16.08%、19.39%和31.02%。由此说明TentSSA-BPNN能耗预测模型具有更高的预测精度。

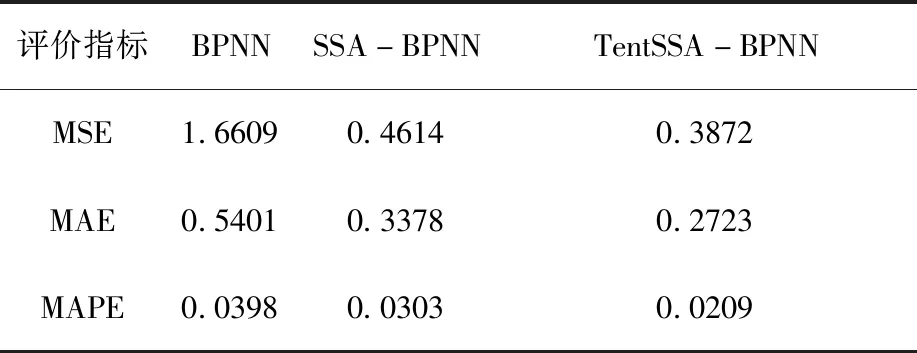
表4 精准度对照

(4) 收敛性分析

在本实验中,输入归一化的数据后可得到模型的预测结果,将结果代入公式(5),求得预测值的MSE。将预测值的MSE作为适应度值并绘制对应曲线,算法求得的适应度值曲线可用来反应算法的寻优情况,SSA-BPNN模型与TentSSA-BPNN模型的收敛性对比结果如图3所示。可以看到,SSA-BPNN模型的适应度值在第34次迭代后陷入了局部最优且无法跳出,TentSSA-BPNN与SSA-BPNN相比则多次跳出了局部最优,并在第37次迭代后计算得到了更小的适应度值。结果说明,本文所提出的TentSSA算法具有更高的寻优精度和更强的全局搜索能力。

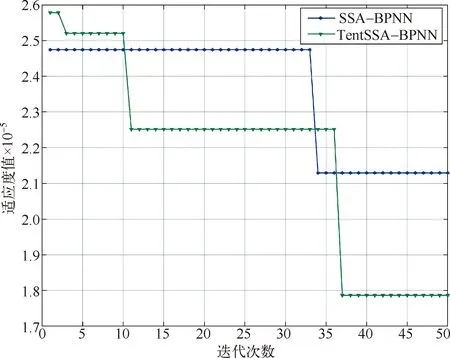
图3 最优个体适应度值对比

5 结论

(1) 基于BPNN建立的基础预测模型,在输入相对应的参数后,可以预测出未来钢铁企业的电量使用情况。但是传统BPNN模型仍存在收敛速度慢和陷入局部最优,以及传统麻雀算法容易“早熟”等问题,因此本文提出了TentSSA-BPNN预测模型。首先将Tent混沌映射函数引入到麻雀搜索算法中,增加了麻雀种群的多样性,优化后的SSA算法的初始麻雀个体得到了更加均匀的分布,有效提升了算法在寻优过程中跳出局部最优的成功率,其全局搜索效果也得到了优化。最后以Tent混沌映射与麻雀算法结合的方式来优化传统的BPNN模型,克服了传统BPNN的固有缺点,提升了预测的准确性。

(2) 本文选取某钢铁企业8064条电力能耗的历史数据,利用提出的TentSSA-BPNN模型进行预测分析,实验结果表明该模型在钢铁企业的电力能耗预测中具有较高的准确性,其预测结果可为后续钢铁企业节能降耗的措施安排提供一定指导。在未来的研究工作中,将会继续优化并构建预测精度更高、收敛效果更好的能耗预测模型。