基于均值未知的高维协方差矩阵的估计

陈艳真，李树有

基于均值未知的高维协方差矩阵的估计

陈艳真，李树有

（辽宁工业大学 理学院，辽宁 锦州 121001）

给出了一种基于均值未知情形下，高维协方差矩阵估计的新算法。即当矩阵的维数大于样本容量时，根据随机矩阵理论，通过样本协方差矩阵特征值的边缘密度函数和总体特征值的对数似然函数，得到目标矩阵特征值的估计量。基于收缩估计的思想，对目标矩阵特征值和样本协方差矩阵特征值进行收缩估计，通过特征值的估计得到高维协方差矩阵的一个新的估计量。数值模拟表明，对于多元正态的总体，高维协方差矩阵的新估计量较样本协方差矩阵的精度更好。

高维协方差矩阵；收缩估计；边缘密度；似然函数；奇异Wishart分布

协方差矩阵的估计是现代统计学中一个重要的参数估计问题，人们在实际应用中会遇到各种类型的海量数据，如股票交易数据、图像处理数据、基因检测数据等，这些数据在统计处理中通常称为高维数据。

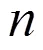
1 高维协方差矩阵估计的一种新方法

1.1 边缘密度

则的密度函数如下：

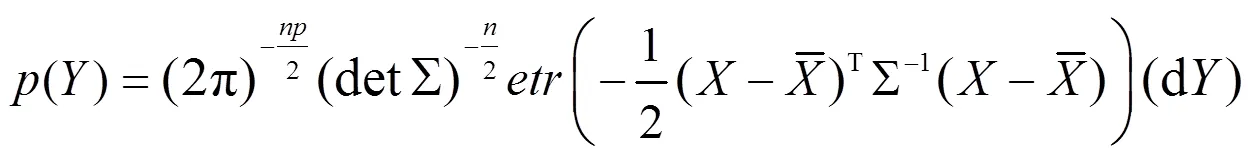
由Muirhead[9]的推论2.1.16，表明具有由密度指定的分布

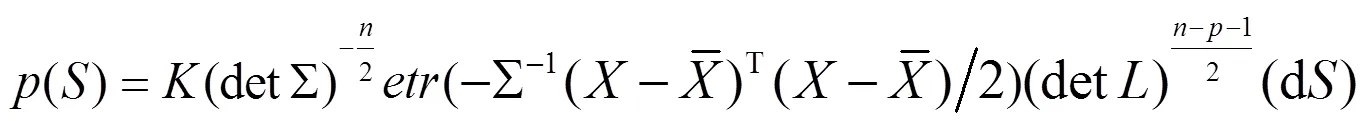
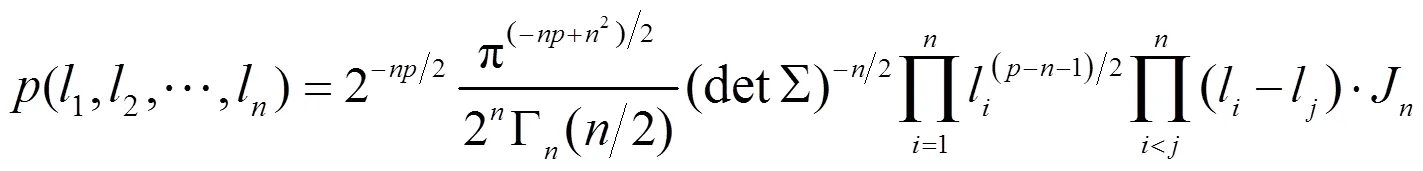
积分J不能以封闭形式计算，此处推导其近似值，对于大, 积分J近似于下面的表达式：

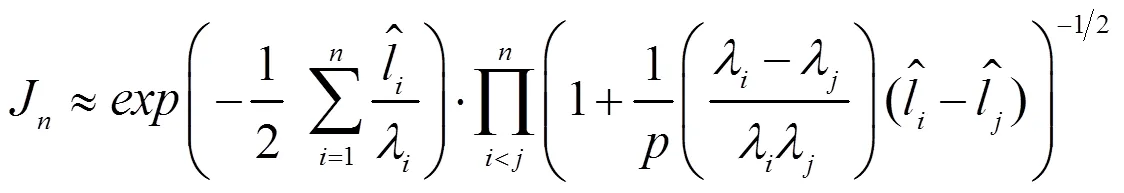
1.2 收缩估计量

在本小节中，主要根据Banerjee等[10]的方法求出总体协方差矩阵特征值的估计量。首先根据上节推导的样本特征值的近似边缘密度，求出总体特征值的近似对数似然函数。

边缘密度函数：

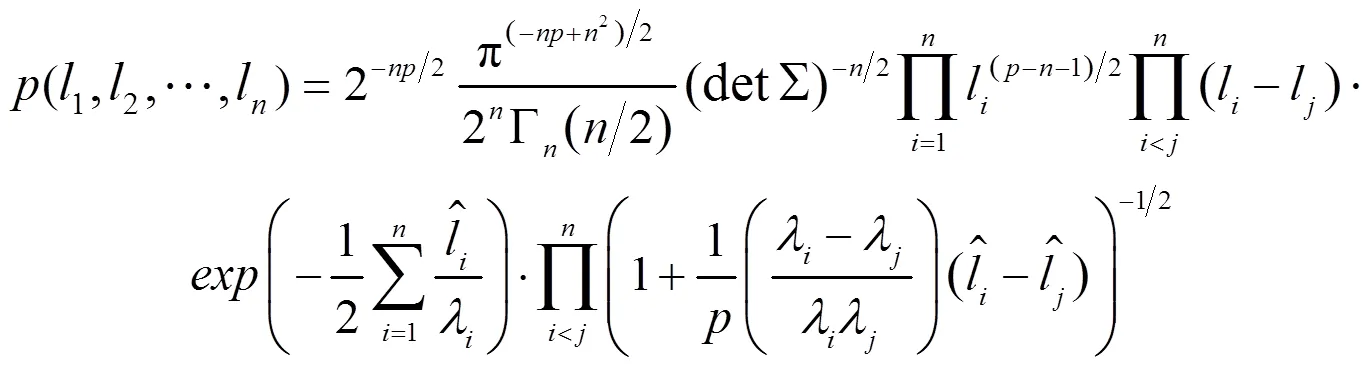
对数似然函数：

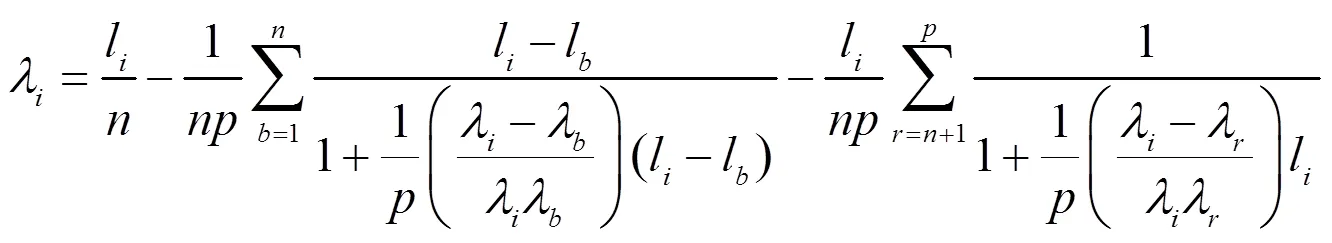
1.3 参数ω的确定

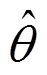
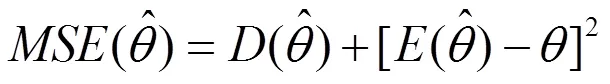
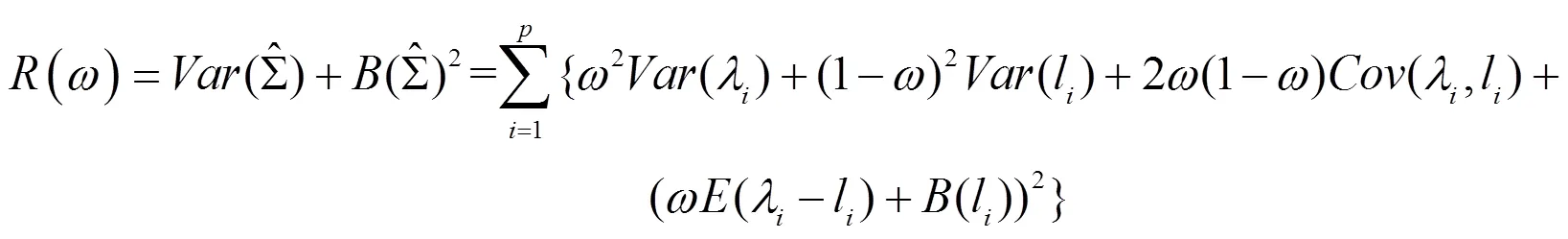
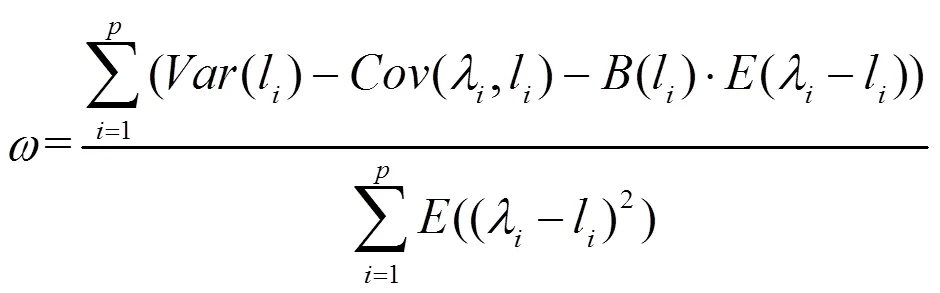
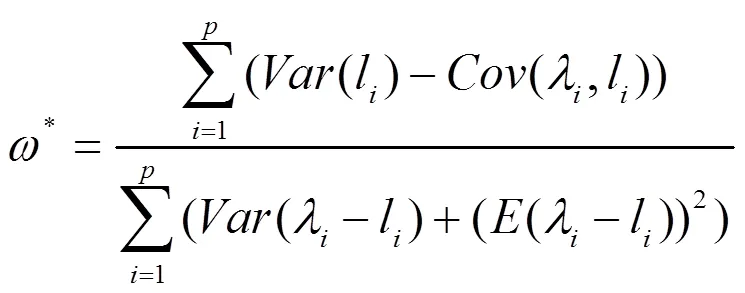
则高维协方差矩阵估计的一种新估计量为

2 数值模拟

表1 数值模拟结果

n205080100200 3.50582.00481.47441.33181.1236 3.47071.98661.47431.33171.1236

3 结论

[1] 茆诗松. 高等数理统计学[M]. 北京: 高等教育出版社, 2006.

[2] Ledoit O, Wolf M. Nonlinear Shrinkage Estimation of Large-Dimensional Covariance Matrices[J]. The Annals of Statistics, 2012, 40(2): 1024-1060.

[3] Ledoit O, Péché S. Eigenvectors of some large sample covariance matrix ensembles[J]. Probability Theory and Related Fields, 2011, 151(1): 233-264.

[4] Ledoit O, Wolf M. Spectrum estimation: A unified framework for covariance matrix estimation and PCA in large dimensions[J]. Journal of Multivariate Analysis, 2015, 139(2): 360-384.

[5] 刘恒, 郭精军. 基于交叉验证收缩法的高维协方差矩阵估计[J]. 统计与决策, 2020, 36(9): 39-42.

[6] Ledoit O, Wolf M. A well-conditioned estimator for large-dimensional covariance matrices[J]. Journal of Multivariate Analysis, 2004, 88(2): 365-411.

[7] Schäfer J, Strimmer K. A shrinkage approach to large-scale covariance matrix estimation and implications for functional genomics[J]. Statistical applications in genetics and molecular biology, 2005, 4(1): 1-32.

[8] Uhlig H. On singular wishart and singular multivariate beta distributions[J]. The Annals of Statistics, 1994, 22(1): 395-405.

[9] Muirhead R J. Aspects of Multivariate Statistical Theory[M]. New Jersey: John Wiley and Sons Inc, 1982.

[10] Banerjee S, Monni S. An orthogonally equivariant estimator of the covariance matrix in high dimensions and for small sample sizes[J]. Journal of Statistical Planning and Inference, 2021, 213(26): 16-32.

Estimation of High Dimensional Covariance Matrix Based on Unknown Mean

CHEN Yan-zhen, LI Shu-you

（College of Science, Liaoning University of Technology, Jinzhou 121001, China）

A new algorithm for estimating high dimensional covariance matrix based on unknown mean is presented. That is, when the dimension of the matrix, p, is larger than the sample size n, according to the random matrix theory, the estimators of the eigenvalues of the objective matrix are obtained through the marginal density function of the eigenvalues of the sample covariance matrix and the logarithmic likelihood function of the population eigenvalues. Based on the idea of shrinkage estimation, the eigenvalues of target matrix and sample covariance matrix are estimated, and a new estimator of the high-dimensional covariance matrix is obtained by estimating the eigenvalues. Numerical simulation shows that the new estimator of high-dimensional covariance matrix is more accurate than the sample covariance matrix for multivariate normal population.

high-dimensionalcovariance matrices; shrinkage estimation; marginal density; likelihood function; singular Wishart distribution

10.15916/j.issn1674-3261.2023.02.012

O212

A

1674-3261(2023)02-0136-05

2022-10-21

陈艳真(1997-)，女，河南驻马店人，硕士生。

李树有(1964-)，男，辽宁锦州人，教授，博士。

责任编辑：刘亚兵