基于节点核心度的重叠社团检测算法

代婷婷，刘 秀，韩 艳

基于节点核心度的重叠社团检测算法

代婷婷，刘 秀，韩 艳

（昭通学院 数学与统计学院，云南 昭通 657000）

针对含有重叠节点的社团提出了新的检测算法—NCD算法。提出了节点核心度的概念，按照节点核心度的计算方法选取簇的初始中心点；提出差异性函数对重叠部分的节点进行识别；在中心点扩展原则的指导下，通过判断网络中节点之间可否构成三角模型对重叠社团进行检测。使用了NMI和模块度作为社团检测的指标，将NCD算法应用在3个真实网络数据集上进行实验，结果表明，NCD算法可以高效地检测到社团中的重叠节点，同时表明了该算法与其他算法对比具有明显的优越性。

复杂网络；社区检测；核心度；重叠社团

近些年来，随着社交网络和大数据技术的发展，大规模复杂网络中的社团检测已经成为研究的热点，社团检测作为复杂网络研究中的一项基本而重要的任务，旨在挖掘集合内连接紧密，集合之间连接稀疏的节点集合[1]。在现实世界的网络中，一些节点可能同时属于多个社团，即重叠的社团结构。因此，检测重叠社团的结构很重要，有助于获取和理解复杂网络的整体结构特征[2]。然而，传统的社团检测算法[3]就不再有效。因为在重叠社区检测中，一个节点可能属于多个社区。随着复杂网络规模的扩大，现有的重叠社区挖掘算法在处理大型复杂网络时效率较低，因此，需要快速准确的算法应对大规模复杂网络中的重叠社团挖掘，目前已经开发了许多用于重叠社区检测的算法，主要包括派系过滤算法[4]、边缘图分割法[5]、局部开展法[6]等，派系过滤算法(clique percolation method，CPM)[7]将社区视为一组全连通子群(completed subgraph)，因此更适合于更充分的网络连通子图。边图划分[8]利用自然边缘的重叠特征，通过生成边缘图通过节点链接到边缘链接的转换，然后划分它们以获得社区结构。而基于局部结构适应度的社区扩展方法(local fitness maximization，LFM)[9]考虑局部结构特征，逐步扩展生成社区，多个扩展社区形成自然重叠。与此同时，LFM也采用了多分辨率策略来辅助用户做出最优选择。除此之外，学者们还提出了一些混合算法[10]，但是，现有的大多数方法基于传统的优化[11]或者启发式算法[12]，不能同时满足速度和精度的要求。因此，本研究提出了一个基于节点核心度的重叠社团检测算法。首先该算法提供了节点核心度的计算方法，然后给出了重叠节点的选取规则，最后在人工网络和实际网络上评估了该算法的性能并且与现有的经典算法做了对比，结果表明，本研究的方法在具有更强重叠的网络上检测效果较优。

1 社团定义

社团结构是网络中显著的结构特征，可以挖掘复杂网络中包含的深层次特性。实际中整个网络通常被视为由若干个社团构成，社团内部节点之间连接稠密，社团间连接稀疏[13]。例如兴趣俱乐部社团，同一个俱乐部成员之间的兴趣相同联系密切而不同俱乐部间兴趣不同则联系相对疏远。对于社团的定义没有统一的表示，在数学角度上对社团结构的简单形式化描述为定义1。

定义1 社团结构，即网络()的一个划分，记为={1,2,...C}，其中，C⊆，U=1=,=||表示网络包含社团的数量。

2 节点核心度计算

定义2(直接影响因子)[13]对于给定的无向图()，其中={1,2,...,}表示图中节点的集合，分别表示节点的总数和边的总数，={1,2,...}代表图中所有节点连边的集合，节点v的度用(v)表示，则节点v、v之间的直接影响因子可定义为：

(vv)表示节点v对v的影响力，(vv)的取值为[0,1]，(vv)=1/(v)。

定义3(节点互信息)[14]在无向图(,)，中节点v与节点v之间的互信息(vv)定义如下：

节点v的全局信息为节点v到图中所有节点的互信息之和，公式如下：

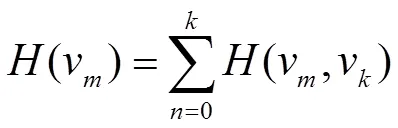
节点的全局信息大小可代表节点在整个网络图中的影响力大小，在有了节点的核心度与节点的全局信息相关概念后，由于节点对图中的其他节点的核心度有一定的影响。因此，本文将核心度影响矩阵表示成邻接矩阵的形式。经过综合考虑节点的直接影响力和节点的全局信息后，节点的核心度影响矩阵可用如下公式计算：

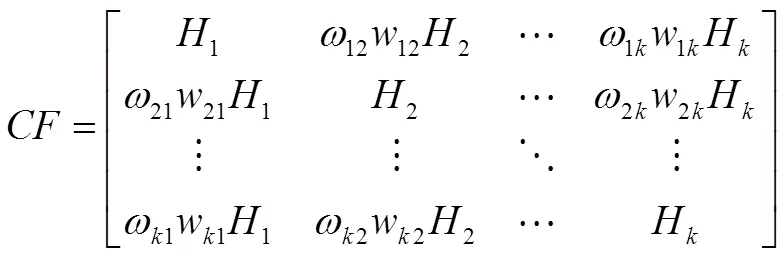
在式(4)中，若节点v、v之间有边连接，则ω=1；否则ω=0。W为节点对节点的直接影响力，节点的核心度影响矩阵代表图中每个节点对其余节点核心度的影响程度，因此，节点v的核心度C可按照下式计算：

根据C的表达式可知，节点本身的全局信息与其所有邻接节点对节点的核心度影响的和的平均值构成了节点的核心度。

3 检测重叠节点的方法

对于重叠社团来说，其中的每一个重叠节点v周围都存在与之差别不大的中心节点可供选择。所以，可通过比较节点v与各个中心节点的差异度进行选择重叠节点，其中差异性函数的计算公式为：

在式(6)中，C为社团检测过程中断定给节点v的中心节点，C表示为其他社团所在的中心节点，d、d分别表示为节点C与C的度，(v,C,C)表示对于节点v而言，选择节点C与节点C作为中心节点的差异性。在上面定义的基础上，本文给出了判断重叠点的标准：

其中C≠C，参数为事先设定的阈值，∈[0, 0.1]，当在不同的范围内取值时可以得到不同数目的重叠节点，即可通过的不同取值对重叠节点的数目进行调整。若式(7)成立，则可得到节点v是重叠节点，C或C为其中心节点。

4 核心度社团检测算法（NCD）

4.1 算法步骤描述

本文的算法是基于聚类的思想检测复杂网路的重叠社团，所以本文在重叠社团的检测中运用了节点的核心度，节点的核心度越大，则表明其极有可能成为聚类中心点。首先在算法的每一次迭代过程中选取核心度大的节点作为簇初始中心点，然后根据中心点扩展原则[3]判断初始中心点周围的节点是否属于同一个社团，于是就可得到社团的划分；在完成社团的划分之后还可以利用差异性函数检测具体的重叠节点。具体的检测实现过程如下。

(1)根据公式(5)计算所有节点的核心度，然后按照降序排列的方式将节点的核心度放到队列中。

(2)选取具有最大核心度的节点作为可扩展中心点，当该节点没有被划分的时候，就将该节点作为初始化社团的中心不断扩展社团。

(3)当以中心节点v与其邻接节点v以及它们的共有邻接节点v之间够成三角模型时，其邻接节点就可以添加到以节点v为中心的所属社团中，如果v、v、v没有构成三角模型则，则邻接节点v不会被分配到该社团。

(4)不断重复以上步骤，当队列中的节点核心度小于全部节点核心度的平均值的1/2时算法停止。

综上所述，重叠社团检测算法伪代码。

算法：NCD算法

输入：无向图()，优先队列，节点数量，阈值。

输出：节点集合的社团划分记为{}=1，其中为算法检测到的社团数量；重叠节点的集合{OPS}=1。

for每个节点v

使用公式(5)计算节点核心度C，将C按照降序排列放入优先队列中，

end for

计算所有节点核心度的平均值，记为C；

for vin；

ifC<C/2

break；

ifv未被分配到任何一个社团

重新开启一个新社团的初始化，并且标注节点v所在的社团数目

ifv只存在于1个社团内

则把v作为初始中心点，依据中心点可扩展原则扩展中心节点v，并标注v所在社团的数目；

else将节点v标注为非中心节点

end for

检测未被划分的节点

if(v)=0

标记v为独立社团；

if(v)=1

将节点v划分到其邻接节点v所在社团；

得到划分后的社团{}=1，并将中心节点存储在集合中

for每一个社团V∈{}=1

对重叠节点集合初始化，使{OPS}=1=

end for

for每一个节点v∈

for每一个中心节点v∈

根据公式(6)计算=(v,C,v)

if |d-|/≤或|dv-|/≤且v≠C

if|d-|/≤或|dv-|/≤且v≠C

OPS=OPS∪{v}

end for

end for

最终得到重叠点的集合{OPS}=1以及划分后的社团{V}=1

4.2 算法时间复杂度分析

给定无向图(,)，、分别为网络的顶点总数和网络包含的节点边数，假设全部节点核心度的平均值为。计算完所有节点核心度的时间复杂度为(3)，对所有节点核心度按照降序排列的时间复杂度为(log)；在对节点进行扩展过程中，查询节点的邻接节点以及扩展的时间复杂度为(2)；标记重叠节点所在的社团数量的时间复杂度为()；划分未分配的节点时，其时间复杂度为()。综上所述，完成整个算法的时间复杂度为(3)。

5 实证分析

5.1 实验方法介绍

为验证NCD算法的性能，本文在真实数据集上进行社区检测实验，并与其他算法的社区检测结果进行对比，采用标准化互信息(NMI)指标和模块度指标对比评价。为更直观地验证NCD的实现效果，分别选取GN、ACC、NLA算法进行对比。算法各运行20次，并取最大值的平均值进行对比，减小算法随机性对结果的影响。

5.2 实验数据集

本文用到3个真实网络数据集来自于http:// www.personal.umich.edu/～mejn/net data/的Karate、Dolphins和Football网络，具体信息如表1。

表1 真实网络的相关信息

网络节点数边数社团数 Karate34782 Dolphins621594 Football11561312

5.3 评价指标

(1)标准化互信息(normalized mutual information，NMI)。标准化互信息指标[1]是对已知网络结构的社区检测评价的经典指标。该指标主要衡量算法所检测到的网络社团结构与真实社团结构之间的相似程度。的取值在0～1之间，其值越大表明检测到的网络结构和真实结构越接近。

式(8)中，表示实际社团情况，表示算法检测的社团情况，C和C分别表示和的真实社团数目，m表示混乱矩阵中的元素，m表示混乱矩阵中第行的总和，m表示混乱矩阵中第列的总和，表示网络的节点个数。

(2)社区模块度()。对于真实的网络数据集本文采用Newman提出的模块度进行评价。模块度是衡量社团检测算法划分结果优劣的一个指标，的取值范围为[-0.5, 1.0)，在实际应用中的最大值一般为0.3～0.7。其取值越大表明划分出的结果越好。检测重叠社团的模块度函数的计算公式如下所示：

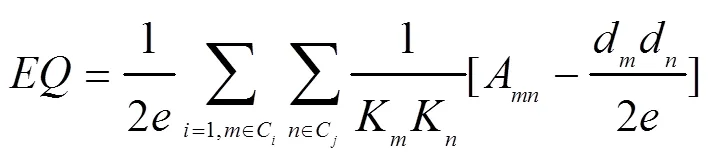
式(9)中，表示网络的边数，a表示网络邻接矩阵中的元素，当和相连时a=1，否则为0，表示隶属函数，当节点和属于同一个社团时δ=1，否则为0。

5.4 实验结果及分析

为了说明本文算法的有效性，对NCD算法在Karate、Dolphins和Football网络3个切实有效的数据集上的检测结果进行了分析。

图1表示的是本文算法在Karate数据集上的社团划分结果，阈值参数的值设置为0.80，NCD算法将该网络划分成2个社团1和2，其中社团1的中心节点为2，2社团的中心节点为33，2个社团重叠的节点为3和10。

图1 karate网络重叠社团检测可视化结果

本文的NCD算法在Dolphin网络数据集上的社团检测可视化结果如图2所示，其中参数=0.08，由图可知该算法将Dolphin网络划分成了红色和黑色2个社区，它们的中心节点分别为节点39和节点18；2个社团的重叠节点为紫色的{20, 40, 8}。

图2 Dolphin网络重叠社团检测可视化结果

图3为NCD算法在足球俱乐部网络上进行社团检测的可视化结果，当参数取值为0.08时，该算法将该网络划分成11个社团，分别用不同的颜色代表，检测到的重叠节点为80与82。

为了进一步突出本文所提算法的优越性，本文中选用AC、GN、NLA 3种算法与本文的NCD算法做对比，首先将参数统一设置为0.08，然后将3个对比算法及本文提出的NCD算法运用在3个切实有效的数据集上执行6次，并对其平均值结果进行对比。对比结果如图4所示，从图4中可以看出各算法分别在3个真实有效的数据集上模块度的具体取值，模块度的值越高说明社团的划分结果越准确；由图可知，在3个数据集上实验结果表明本文算法的模块度值比其他3种算法的模块度值都高，即4种方法中NCD算法划分的社团准确率最高。Zachary网络数据集上的实验结果表明，4种方法比较中GN算法和ACC算法的模块度值比较低，特别是GN算法的模块度值低于0.3，说明了GN算法和ACC算法对Zachary网络的划分结果的准确性较低；在海豚网络数据集实验中，GN算法的模块度值为0.422最低，即该算法划分效果最差，另外2种算法ACC算法和NLA算法的模块度分别为0.481和0.499，说明这2种算法的划分效果相当；在College Football网络的检测中，本文的NCD算法的模块度值为0.597最高，说明该算法具有良好的社团检测性能。其次，NLA算法的模块度值为0.533，比其他2种算法的模块度值都高，说明其划分效果较其他2种算法良好；整体来讲，GN算法在3个数据集上的模块度值最低，由此可知GN算法不能检测出高质量的社团结构。

图4 3个有效数据集上的模块度值比较

度量社团划分准确性的指标除了模块度之外还有NMI值，当NMI值越大时说明其划分的社团结果越精确。4个对比算法在Zachary、Dolphin和College Football 3个真实有效的数据集上得到的NMI值比较结果如图5所示，Zachary网络数据集上，NCD算法的NMI值为0.601，比其他3个算法的值都高，说明此算法社团检测结果准确率比其他3种算法都高；NLA算法的NMI取值略高于ACC算法；GN算法的NMI值为0.489最低，说明其社团划分结果最差；在Dolphin数据集上，NCD算法的NMI值为0.596，比ACC算法的值略高，而GN算法的NMI值0.502最低检测效果最差；在College Football网络中，NMI值最高的算法为NCD，该算法的NMI值达到了0.876，说明其测到的社团与真实的网络社团结构最接近，4个比较算法中GN算法的值为0.718最低，由此可以推出此算法在网络的社团结构划分上有效性最差。

6 结论

针对复杂网络中的重叠社区检测，本文提出了一个基于节点核心度的社团检测算法—NCD算法。首先给出了节点核心度的定义以及核心度的计算公式，并将核心度值按照降序顺序排列；其次依据中心点可扩展原则判断节点之间能否构成三角模型对网络进行初步的重叠社团检测；最后在已经划分好的社团上识别网络的重叠节点。为了验证本文所提算法具有良好的复杂网络重叠社区检测能力，在Karate、Dolphins和Football网络3个切实有效的数据集上进行了实验并且与AC、GN、NLA 3种算法做了对比分析，试验结果表明，与选用的3种比较算法相比，NCD算法都具有较高的模块度值和NMI值，即本文的NCD算法不但能够检测出重叠性强的网络社团结构，还能有效地检测出具体的重叠节点。

[1] STROGATS H. Exploring complex networks[J]. Nature, 2001, 410: 268–276.

[2] FORTUNATO S. Community detection in graphs[J]. Phys, 2010, 486(3): 75-174.

[3] FANG Y, HUANG X, QIN L, et al. A survey of c ommunity search over big graphs[J]. Vldbj, 2020, 29(8): 353–392.

[4] LI H J, WANG L, ZHANG Y. Optimization of identififiability for effificient community detection[J]. Physical(A), 2020, 22(6): 063035.

[5] CAO J, DING D, LIU J. Hybrid triggered based security controller design for networked control system under multiple cyber attacks[J]. Inf Sci, 2021, 548: 69–84.

[6] CAO J, BU Z, WANG Y, et al. Detecting prosumer community groups in smart grids from the multiagent perspective[J]. Systems Man Cybernetics, 2019, 49(8): 1652–1664.

[7] CAO J, WANG Y, HE J, et al. Predicting grain losses and waste rate along the entire chain: a multitask multigated recurrent unit autoencoder based method[J]. Statistical Analysis and Data Mining, 2020, 17(16): 12-16.

[8] PALLAL G. Uncovering the overlapping community structure of complex networks in nature and society[J]. Nature, 2005, 435(7043): 814–818.

[9] AHN Y Y, BAGROW J P, LEHMANN S. Link communities reveal multiscale complexity in networks[J]. Nature, 2010, 466(7307): 761–764.

[10] PSORAKIS I, ROBERTS S, EBDEN M, et al. Overlapping community detection using Bayesian non-negative matrix factorization[J]. Phys Rev E, 2011, 83(5): 66-114.

[11] LIU W, WANG Z, YUAN Y, et al. A Novel Sigmoid- Function[1]Based Adaptive Weighted Particle Swarm Optimizer[J]. Trans Cybern, 2021, 51(2): 1085–1093.

[12] SUN J, XIE Y, ZHANG H, et al. Less is more: Sparse graph mining with compact matrix decomposition[J]. Statistical Analysis and Data Mining, 2008, 1(1): 6-22.

[13] GREGORY S. An Algorithm to Find Overlapping Community Structure in Networks[C]// European Conference on Principles of Data Mining & Knowledge Discovery. Springer, Berlin, Heidelberg, 2007.

[14] 蒋盛益, 杨博泓, 王连喜. 一种基于增量式谱聚类的动态社区自适应发现算法[J]. 自动化学报, 2015, 41(12): 2017-2025.

Overlapping Community Detection Algorithm Based on Node Core Degree

DAI Ting-ting, LIU Xiu, HAN Yan

（Mathematics and Statistics College, Zhaotong University, Zhaotong 657000, China）

A new detection algorithm-NCD algorithm is proposed for the community with overlapping nodes. The concept of node core degree is proposed, and the initial center point of cluster is selected according to the calculation method of node core degree. The difference function is proposed to identify the overlapping nodes. Under the guidance of the central point extension principle, the overlapping community is detected by judging whether a triangle model can be formed between nodes in the network. NMI and modularity are used as indicators of community detection, and the NCD algorithm is applied to three real network data sets. The results show that the NCD algorithm can efficiently detect overlapping nodes in the community, and it also shows that the algorithm has obvious advantages compared with other algorithms.

complex network; community detection; coreness; overlapping communities

10.15916/j.issn1674-3261.2023.02.011

TP124

A

1674-3261(2023)02-0130-06

2022-10-01

代婷婷(1986-)，女，甘肃庆阳人，讲师，硕士。

责任编辑：孙 林