基于MEA－BP 神经网络的印刷车间能耗预测

张明月， 贺福强， 李思佳， 聂文豪

（1 贵州大学 机械工程学院， 贵阳 550025； 2 贵州西牛王印务有限公司， 贵阳 550008）

0 引言

在全球经济迅速发展变革的洪流中，制造业作为国内国民经济的基础正面临巨大的挑战。 能量资源是国民经济的命脉，是经济发展中至关重要的战略资源，因此节约资源、保护环境、实现可持续发展已成为当发展共识。 据统计，国内人均能源资源拥有量处于较低水平［1］。 但是，国内的人均能耗比国际平均值要大得多，而且国内经济发展正处在高度智能化和工业化的进程中。 处于当前状态下的能源问题尤为紧迫，如何有效提高能源使用的效率已成了所有企业持续关注的重点问题。 在印刷企业实施绿色节能、智慧管理的过程中，往往需要预先确定下一阶段或未来季度的能耗量，从而为企业制订节能战略和进行节能效果评估提供依据。 因此，为了达到企业节能降耗的目的，必须采取一种科学合理的运行方案。 作为节能控制优化的基础，能耗预测也是印刷企业长久运行的关键，在印刷工艺的节能优化中具有决定性和根本性的作用。

1 MEA 算法优化BP 神经网络模型

1.1 MEA 算法原理

与传统的搜索算法比较，思维进化算法［2－4］可以模仿人类思考。 思维进化算法（MEA）主要的系统框架如图1 所示。 由图1 可看到，该架构的组成部分主要有：由参数空间、个体元素、子群体、公告板以及特征提取。

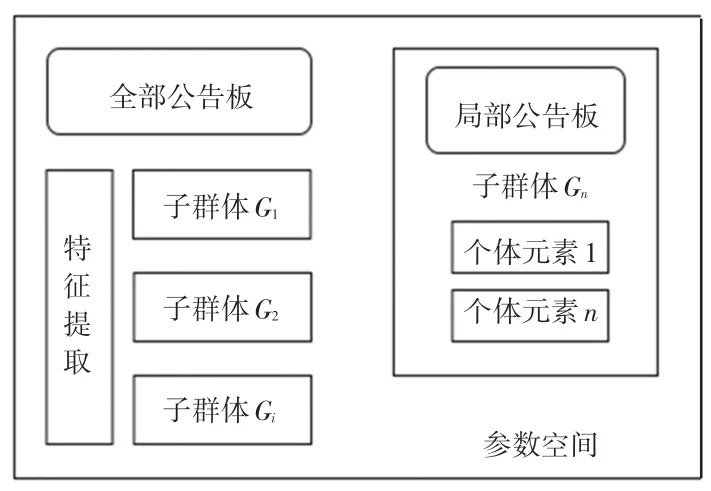
图1 思维进化算法系统结构图Fig. 1 System structure diagram of thinking evolution algorithm

这个算法的要点是：“趋同”和“异化”，并分别在不同的空间范围内作业。 其中，趋同是在子群体内的局部操作。 这种运算存在于每个子群体中，组内个体元素竞争成为最优胜个体，并将最优胜个体作为目标随机进行搜索，如果经过连续几代，一个子群体的得分未见明显增长，则说明该子群体内没有生成新的最优胜个体，那就可以将该子群体看作成熟的子群体。

相比于趋同的生效范围，异化是在全局环境中生效。 在整个参数空间中，各个子群体通过连续不断地搜索新的个体的方法，不断更新最优胜子群体。如果经过数代的临时子群得分，没有一个能替代已有的优胜子群体，那么该个体就会到达最佳状态，并求得了思维进化的最优解。

思维进化算法的核心理念是对参数空间进行持续的进化，通过不断探索进化产生更多优质个体，从而得到最优个体。 也就是通过“趋同”与“异化”的操作，经过反复计算，生成新的个体的子群体，并从中寻找出最佳的解决方案。

1.2 BP 神经网络原理

BP（Back Propagation）算法［5－9］、即误差反传算法，是当前较为常用的一种学习算法。 研究可知，BP 算法的实现可以分为2 个步骤：前向传播信号和反向传播误差。 采用BP 神经网络对印刷过程进行能量消耗的预测。 BP 神经网络一般采用输入层、隐藏层和输入层。 BP 神经网络拓扑结构如图2 所示。

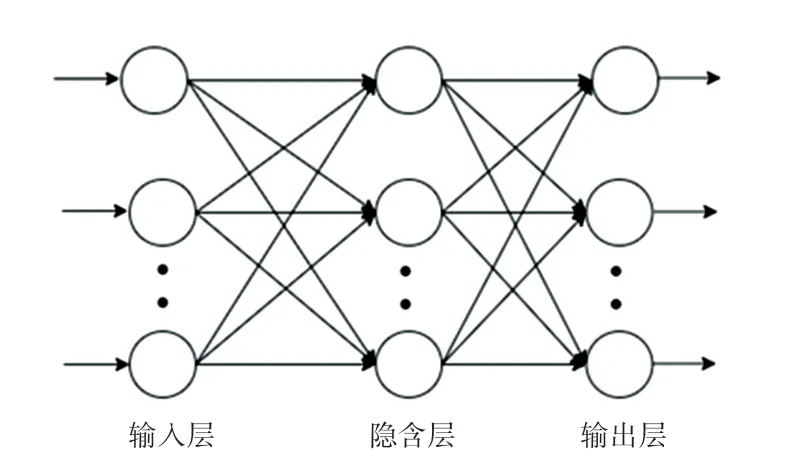
图2 BP 神经网络拓扑结构图Fig. 2 Topological structure of BP neural network

在实际中，对于具有一定滞后性的非线性系统，建立一层隐藏层的神经网络就可以做到精准预测。所以，在本论文所要探讨的印刷能耗，只需要建立一层隐藏层即可。 因此，研究选用3 层神经网络作为预测模型。 研究者们主要是依据过去的研究和模型的预报结果来调整BP 神经网络中的神经元数目。通过式（1）计算得到隐含层的神经元个数：

其中，l表示隐含层神经元个数；m表示输出层神经元个数；n表示输入层神经元个数；a为常数，通常取2～10。

1.3 优化思路

本部分主要分析了BP 神经网络存在的问题，并对其进行了优化和改进。 BP 神经网络作为一种预测算法虽然有一定的优势，但是在某些方面也存在不足。 对此拟展开阐释分述如下。

（1）BP 神经网络训练过程中容易产生局部极小值。 该算法将误差信息传递到权值和阈值处，为下一次的调节提供数据和方向，属于“下坡”的做法。 因此网络很容易陷入局部化，无法达到全局最小值。 该过程示意如图3 所示。

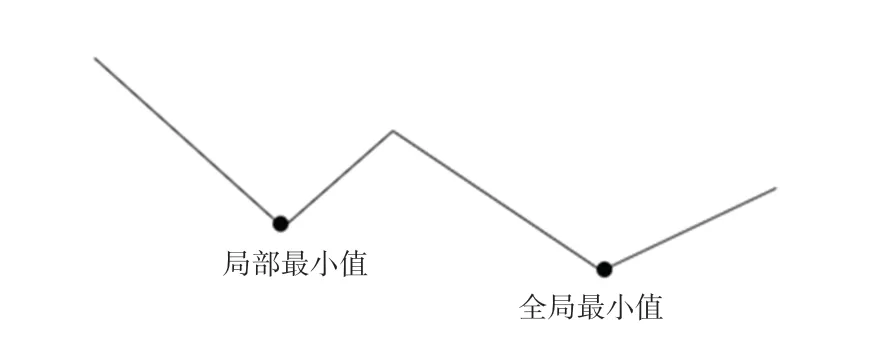
图3 BP 神经网络训练过程示意图Fig. 3 Schematic diagram of the training process of BP neural network

（2）网络的学习收敛性差，学习时间长。 为了保证算法的收敛性，BP 神经网络在学习率控制上存在一定的局限性，当遇到特定问题时，学习时间可能较长。

（3）无法保证网络的泛化能力。 BP 神经网络的泛化能力受网络设置参数、样本质量、网络初始值等因素的影响。

针对BP 神经网络存在的问题，本文采用思维进化算法（MEA）对BP 神经网络进行了改进。 通过对其权值、阈值进行优化，以期得到全局最优结果。思维进化算法利用算法解空间内多个子群体共同寻找最优值个体。 算法通过采用“趋同”以及“异化”的有机结合，优化神经网络初始权值和阈值。 既可以有效地改善BP 神经网络的收敛率和泛化能力，又保证了权值和阈值的全局代表性，从而改善了BP神经网络的预测准确率。

1.4 MEA－BP 神经网络算法

MEA－BP 神经网络［10－15］的建模中，最重要的是利用MEA 算法的全局寻优的优点，得出最优解。 解码作为BP 神经网络的初始权值和阈值，保证初始值的合理性，进而提高模型的准确率。 其中，MEABP 神经网络算法流程如图4 所示。 由图4 可知，其操作流程具体如下。

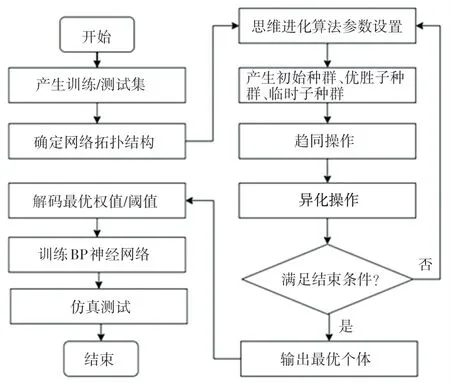
图4 MEA－BP 神经网络算法流程图Fig. 4 Flowchart of MEA－BP neural network algorithm

步骤1产生训练样本集。

步骤2确定网络的拓扑结构。

步骤3产生初始种群、临时子种群和优胜子种群。

步骤4各个子群体内部完成趋同操作，即子群内部不再产生新的最优解个体。

步骤5执行子群体之间的异化操作，并依据该运算产生的结果进行组合产生新的子群体，从而保持数量稳定。

步骤6判断是否满足结束条件。

步骤7解析最优解个体，运用临时子群体与优胜子群体之间的互相竞争、更新得到最优解，解码最优权值和阈值。

步骤8BP 神经网络的训练。

步骤9MEA－BP 神经网络预测模型的预测。训练结束后，输入样本测试数据，进行预测，并进行相关分析。

2 实验结果与分析

2.1 数据处理

在数据预处理过程中，原始数据的标准化是一个重要环节。 不同的评估指数往往存在着差异性，使用不同维度的数据资料进行分析会对数据资料的处理效率产生一定的负面作用。 为了避免数据的不同维度带来的影响，需要对数据资料进行归一化处理。 本文采用归一化的方法，将原始数据线性转换为0～1 之间的自然数。 数据处理方法见式（2）：

其中，X为处理后的数据；xi为输入数据；xmax为最大值；xmin为最小值。

2.2 算法参数设计

主要选用3 层前馈神经网络建立了印刷工艺能耗预测的BP 神经网络模型，由于影响印刷车间能耗的因素主要有5 种，分别是：产量、工人工作时间、设备运行时间、设备加工时间、加工能耗。 因此本实验确定输入层输入个数为5，输出层的神经元个数为1，即能耗预测量。 利用式（2）得到隐含层神经元个数为5。 基于以上参数选择，设计了MEA－BP 神经网络的拓扑结构如图5 所示。

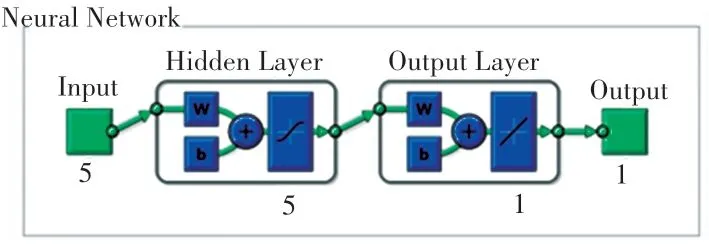
图5 神经网络拓扑结构Fig. 5 Neural network topology

思维进化算法的参数设置见表1。

表1 算法参数表Tab. 1 Parameters table of the algorithm

2.3 结果分析

确定了BP 神经网络的训练参数以及MEA 算法参数设计后，选择建立在Windows10 系统上的Matlab 软件进行实验仿真，软件版本选择Matlab R2018a。 模型首先随机产生初始种群，对10 个子种群分别进行趋同。 选择ismature函数判断是否继续进行趋同。 若子种群尚未成熟，则以新的中心产生子种群；若已经成熟，则子种群的趋同结束。 对子种群的趋同操作如图6 所示。

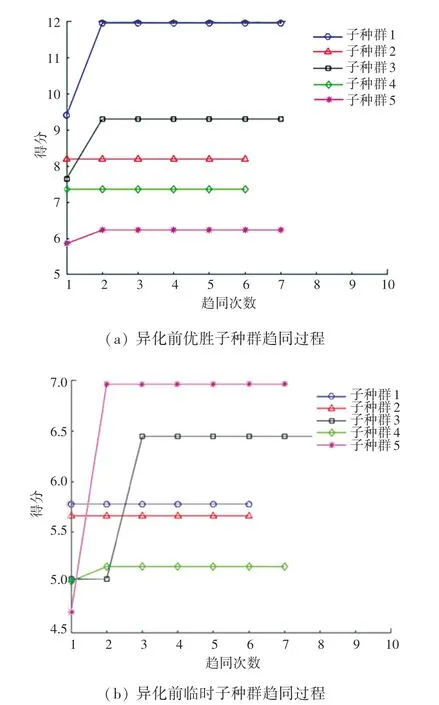
图6 异化前子种群趋同过程Fig. 6 Subpopulation convergence process before dissimilation

寻找临时子群体得分高于优胜子群体的编号，由图6 可以看出，优胜子种群5 的得分较低。 因此需要异化，将得分高的临时子种群替换到优胜子种群中去，而临时子种群则需要重新生成一组子种群，以满足数量不变。 异化操作如图7 所示。

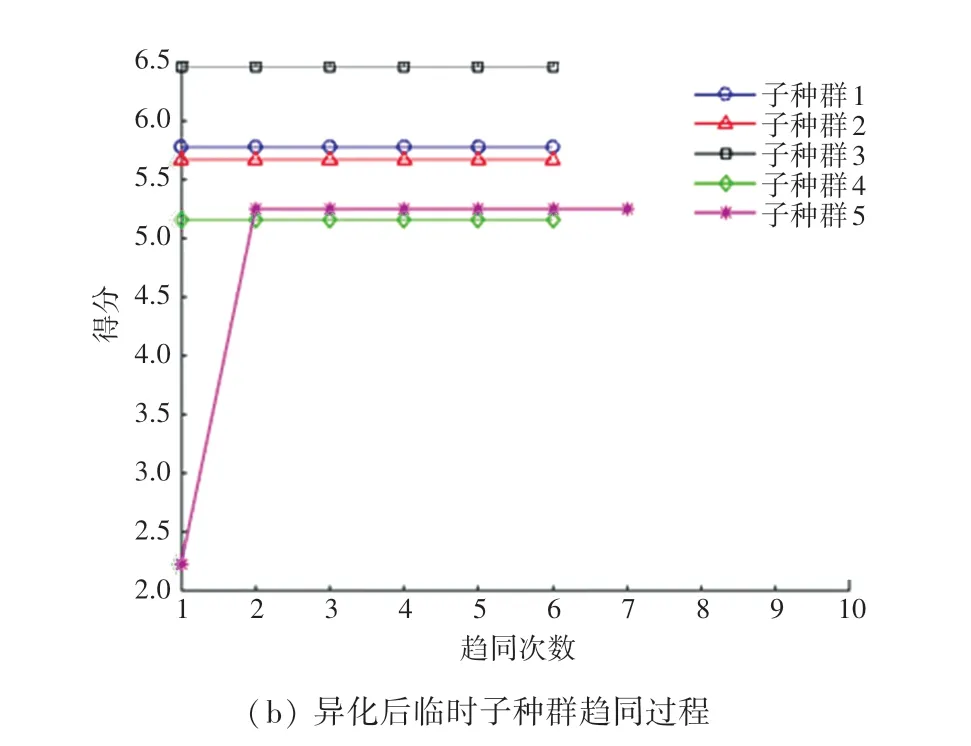
图7 异化后子种群趋同过程Fig. 7 Subpopulation convergence process after alienation

输出思维进化算法当前迭代获得的最佳个体，对其进行解码。 将其设置为网络的初始权值和阈值。 利用印刷车间能耗数据样本对MEA－BP 神经网络进行训练，输出预测结果与样本值的数据对比如图8 所示。

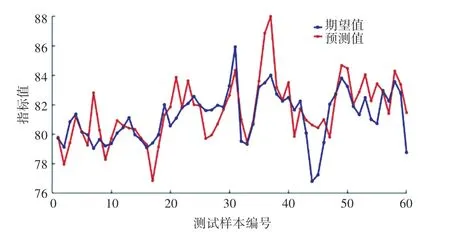
图8 预测结果对比图Fig. 8 Comparison of prediction results

选用相同训练参数、设置相同拓扑结构的BP神经网络，采用相同的能耗数据样本进行训练，得到该模型下的输出数据。 将2 种模型的输出数据进行对比，见表2。

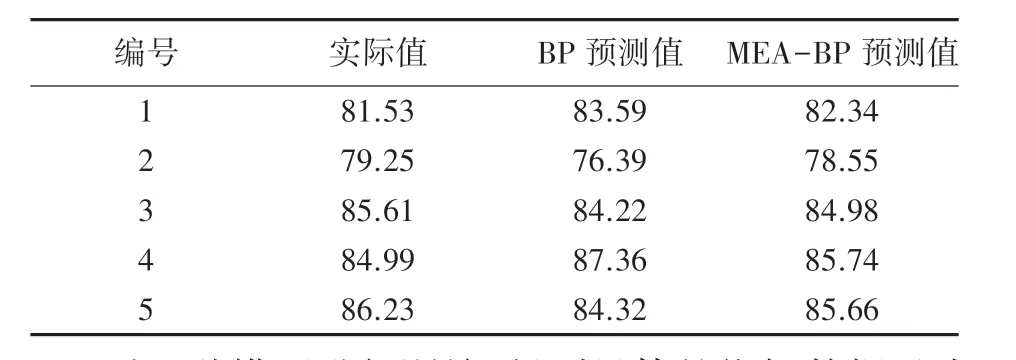
表2 输出数据对比Tab. 2 Output data comparison

对2 种模型进行训练，得到具体的指标数据见表3。 表3 中，MAE为平均绝对误差，RMSE为均方根误差，R为相关系数。 相比之下，MEA－BP 神经网络模型的MAE与RMSE的数值较小，R值较大，表明该改进模型回归性能较好，与数据的拟合度较高。

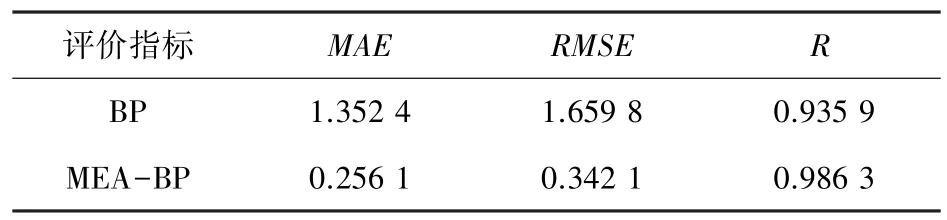
表3 模型评价指标Tab. 3 Model evaluation indicators

3 结束语

本文针对印刷车间的能耗进行预测分析，基于影响因素的复杂性，能耗特质分布规律不明显。 选用MEA 算法对BP 神经网络进行改进，利用MEA算法的全局寻优的优点，得出最优解。 将其解码作为BP 神经网络的初始权值和阈值，保证初始值的合理性，进而提高模型的准确率。 通过仿真实验，根据模型评价指标，可以得到：与BP 神经网络相比，MEA－BP 神经网络的误差更小，在印刷车间能耗预测方面有一定的实用价值。