不同来流角度下方形排列四圆柱的水动力特性

王成彦，巫凯旋，陈沛楷，黄 技

（广东海洋大学船舶与海运学院，广东湛江 524005）

0 引 言

圆柱绕流是流体力学研究领域的一个经典问题，在海洋工程和土木工程等领域中有着广泛应用［1］。近年来，随着陆地上的石油和天然气资源日益枯竭，石油开采不断向深海发展，多柱体系统在海洋平台及海底管线中得到了广泛应用［2-3］。方形排列的四圆柱是海洋工程中的一种典型结构，广泛存在于各种海洋工程结构物中，如延伸式张力腿平台。柱体绕流产生的疲劳破坏可能会威胁人员的安全，造成巨大的财产损失，危害海洋环境，因此研究四圆柱的扰流现象具有重要意义。

近年来，国内外学者针对圆柱绕流问题开展了大量研究。随着计算机技术的快速发展，数值模拟手段成本低、实施方便的优点逐渐显现，各种数值方法得到了较快发展。韩兆龙等［4］采用谱单元法对多圆柱绕流进行了研究；龚志军等［5］采用格子Boltzmann法对低雷诺数下四圆柱的绕流模式及受力特性进行了模拟；贾晓荷等［6］采用大涡模拟的方法对采用不同排列方式的双圆柱的绕流进行了仿真和计算；谢启迪等［7］在OpenFOAM环境下采用RANS方法对不同雷诺数下的单圆柱绕流进行了分析；WANG等［8］从试验的角度出发，对雷诺数为8 000 时的方形排列四圆柱绕流进行了物理实验；殷长山［9］采用粒子图像测速（Particle Image Velocimetry，PIV）技术对不同迎流角下的四圆柱绕流进行了试验研究；LAM等［10］对不同间距比（1.6 ～5.0）下雷诺数为200 时的四圆柱绕流现象进行了研究，得到遮蔽模式转化为再附着模式的临界间距比为2.0，再附着模式转化为漩涡拍击模式的临界间距比为3.5。

虽然已有学者［9，11］对不同迎流角下的方形排列四圆柱进行研究，但缺少对不同迎流角下的方形排列四圆柱更全面、系统的研究。同时，LAM等［10］和于定勇等［12］在研究间距比对方形排列四圆柱的绕流影响时均指出尾流模式转换的临界间距比为2.0 和3.5，因此对临界间距比和迎流角进行研究非常有意义。

真实的流场大多是在超高雷诺数下出现的，采用大涡模拟（Large Eddy Simulation，LES）或直接数值模拟（Direct Numerical Simulation，DNS）方法会消耗大量计算资源，对计算机的计算能力有很高的要求。本文的研究是在雷诺数为3 900 的情况下开展的，属于亚临界区，尽管该雷诺数与实际雷诺数相差较大，但超高雷诺数下湍流场的特征往往也能在较低的雷诺数下得到体现，因此该研究可供实际工程及以后更高雷诺数的研究参考。本文采用计算流体动力学（Computational Fluid Dynamics，CFD）软件Fluent，重点分析来流角度为0°、15°、30°和45°，间距比分别为2.0 和3.5 时四圆柱的水动力特性。

1 理论基础

1.1 流体控制方程

根据流体力学理论，本文所研究的二维模型的连续性方程为

式（1）中：ui，uj，uk分别为x，y，z三个方向上流体的速度分量，ρ为流体的密度。

假设流场内的温度不变，则只考虑动量方程

式（2）中：u，p，υ分别为速度矢量、压力和运动粘度；∇为哈密顿算子

1.2 湍流模型

本文研究的工况为亚临界区（雷诺数Re=3 900），湍流模型选用RNGκ-ε湍流模型。该模型是采用基于重整化群理论的统计方法推导得出的，其形式类似于standard κ-ε模型，但在ε方程中增加了1 项，提高了高速流动的准确性，考虑了涡流对湍流的影响，提升了漩涡流动的精度，同时为Prandtl 数提供了一个解析公式，而standard κ-ε模型只能由用户指定常值。

1）湍流动能κ输运方程为

2）湍流耗散率ε输运方程为

式（3）～式（5）中：μeff=μ +μt；η =Sκ/ε；S 为应变率，S =（2Eij·Eij）1/2；0.012；Gk为由层流速度梯度而产生的湍流能,αε分别为κ方程和ε方程的湍流Prandtl数。

2 计算模型及算例验证

2.1 计算模型

本文共进行8 个组次的数值模拟，各组次工况设置见表1。所设置的流体域大小为24D×24D（D为圆柱直径），2 个相邻圆柱中心之间的距离为L，Re=3 900，4 个圆柱呈方形排列。具体计算区域见图1。

表1 各组次工况设置

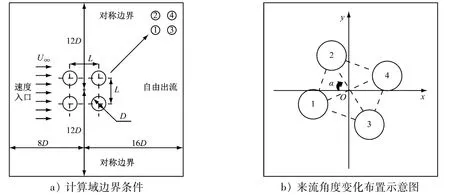
图1 计算区域

本文的压力与速度耦合采用SIMPLE算法实现，压力计算格式采用二阶格式，动量计算格式、湍动能和湍流耗散率均采用二阶迎风格式。瞬态求解采用二阶隐式格式实现。整个流体域采用结构化网格，并在圆柱表面设置边界层网格，以提高计算精度。对圆柱和尾流区域进行局部加密，以得到较精确的尾流形态。整体网格划分和圆柱边界层网格示意见图2 和图3。

图3 圆柱边界层网格示意

2.2 边界条件与初始条件

1）边界条件：入口边界条件为速度入口；出口边界条件为压力出口；上下边界设为对称边界；圆柱表面为无滑移壁面。

2）初始条件：为节省计算时间和提高计算精度，首先进行500 步稳态模拟，并将其作为初始条件，随后进行瞬态计算。

3 数值计算方法验证

为验证湍流模型、网格划分和参数设置的准确性，首先在Re=3 900 的情况下对单圆柱绕流进行模拟，并将所得结果与其他研究结果相对比，结果见表2。随后对Re=3 900、间距比为3.5 的四圆柱绕流过程进行模拟，并将仿真结果与其他研究结果相对比，具体见表3。

表2 Re=3 900 情况下的单圆柱结果验证

表3 四圆柱结果验证

由表2 和表3 可知，本文得到的单圆柱斯特鲁哈数与已有研究结果较为接近，而得到的阻力系数与已有研究结果相比较小，这是由于雷诺平均方程只能提供湍流的平均信息，忽略了湍流脉动量。通过对四圆柱的验证结果进行分析可知，1 号圆柱的阻力系数与文献［12］的研究结果较为接近，3 号圆柱的斯特鲁哈数与其他文献的研究成果均吻合得较好。因此，可验证本文的网格划分、湍流模型选择和参数设置是较为准确的，可进行下一步的研究。

4 计算结果及分析

4.1 流场速度发展云图

当Re=3 900，间距比为2.0 和3.5 时，方形排列四圆柱在不同来流角度下的流场速度发展云图见图4。由于来流角度不同，流场速度云图存在明显差异。当间距比为2.0，来流角度不为0°时，偏斜尾流现象非常明显，上游圆柱没有形成明显的尾涡，下游圆柱脱落的尾涡被延长，四圆柱的尾迹相比来流角度为0°时更明显地被混合在一起。

图4 方形排列四圆柱在不同来流角度下的流场速度发展云图

当间距比为3.5 时，随着间距比的增加，上游圆柱脱落的尾涡“拍击”在下游圆柱上。当来流角度为15°和30°时，尾流区域流场更紊乱，没有对称性，尤其是当来流角度为30°时表现得更强烈。当来流角度为45°时，2 号圆柱与4 号圆柱的尾涡基本对称。由此可见，来流角度不同会极大地影响流场和尾涡的形态。

4.2 升力系数和阻力系数

在圆柱绕流过程中，周期性脱落的漩涡会对圆柱体产生绕流阻力Fd和绕流升力Fl，为方便研究，常进行无量纲化处理，得到阻力系数Cd和升力系数Cl，分别表征圆柱横向和纵向的受力变化。本文通过数值模拟得到临界间距比（L/D=2，L/D=3.5）下，不同来流角度（α=0°，α=15°，α=30°，α=45°）对应的各圆柱阻力系数和升力系数的变化情况。

1）当间距比为2.0 和3.5 时，各圆柱的平均阻力系数随来流角度的变化情况分别见图5a和图5b。

由图5a可知，当间距比为2.0 时，上游圆柱对下游圆柱的遮蔽作用较强，因此上游圆柱的阻力系数相比下游圆柱更大。但是，随着来流角度的增大，2 号圆柱的阻力系数增大，超过了1 号圆柱，这是由于2 号圆柱没有受到1 号圆柱的遮蔽作用，受到了其尾流的影响，且2 号圆柱的阻力系数在来流角度为15°时达到最大之后随来流角度的增大逐渐减小，但仍保持在较高水平，这说明随着来流角度的增大，2 号圆柱实际受到的1号圆柱的尾流影响在减弱。3 号圆柱仍处于1 号圆柱的尾流遮蔽作用下，因此其阻力系数仍较小，在来流角度为30°时也较小。但是，当来流角度增大到45°时，3 号圆柱的阻力系数显著增大并超过1 号圆柱，与2 号圆柱的阻力系数接近。这说明，当下游圆柱摆脱上游圆柱的遮蔽作用之后，仍会受到上游圆柱尾流的影响，导致其阻力系数增大。4 号圆柱受到的遮蔽作用最强烈，因此其阻力系数最小，且随着来流角度的改变，其阻力系数一直保持在较低的水平。由图5b可知，当间距比为3.5，来流角度为0°时，下游圆柱的阻力系数相比间距比为2.0 时的大，这说明上游圆柱对下游圆柱仍有遮蔽作用，但是不如间距比为2.0 时强烈。当来流角度为15°时，2 号圆柱和3 号圆柱的阻力系数与1 号圆柱接近，且当来流角度继续增大时，2 号圆柱和3 号圆柱的阻力系数增大至超过1 号圆柱。4 号圆柱的阻力系数随来流角度的增大先增大后减小，由此可观察到下游圆柱交替受到上游圆柱的遮蔽作用和尾流的影响。

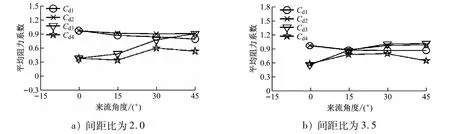
图5 各圆柱的平均阻力系数随来流角度的变化情况

2）当间距比为2.0 和3.5 时，各圆柱的平均升力系数随来流角度的变化情况分别见图6a和图6b。

图6 各圆柱的平均升力系数随来流角度的变化情况

由图6a可知：1 号圆柱的升力系数随来流角度的增大不断增大，2 号、3 号和4 号圆柱的升力系数均是在来流角度为15°时达到最大，随后不断减小；当来流角度为45°时，1 号圆柱与4 号圆柱的升力系数十分接近，与单圆柱的升力系数也十分接近；2 号圆柱与3 号圆柱的升力系数更接近一种相反数的关系，在图像上表现为关于1 号圆柱和4 号圆柱对称。由此可知，2 号圆柱与3 号圆柱是交替向后泄放漩涡的，有一定的对称关系。根据图6b，1 号圆柱的升力系数保持逐渐增大的趋势。2 号圆柱的升力系数随来流角度的增大逐渐增大，并在来流角度为30°时达到最大，随后逐渐减小。3 号圆柱和4 号圆柱的升力系数随来流角度的增大逐渐减小。当来流角度为45°时，各圆柱的升力系数与单圆柱的升力系数趋于相等，这表现出了其在间距比为3.5 时所具有的特点。

4.3 斯特鲁哈数St

St实际上表现了圆柱无量纲化的旋涡脱落频率［4］。通过对所得升力系数作快速傅里叶变换即可得到旋涡脱落频率fx，再进行无量纲化处理即可得到St。St与fx的关系为

式（6）中：D为圆柱直径；U为来流速度；fx为旋涡脱落频率。

本文采用Fluent软件自带的后处理功能，通过导入计算时所得升力系数即可获得St。图7a 和图7b 分别为间距比为2.0 和3.5 时各圆柱的St随来流角度的变化情况。

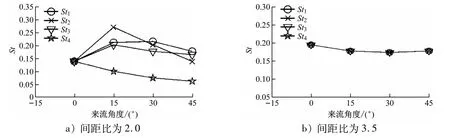
图7 各圆柱的St随来流角度的变化情况

由图7a可知，当间距比为2.0 时，随着来流角度的增大，1 号、2 号和3 号圆柱的St均表现为先上升后下降，而4 号圆柱的St表现为逐渐下降。造成这种现象的原因是在来流角度增大过程中，上游圆柱对4 号圆柱的影响逐渐加大。由图7b可知，虽然随着来流角度的变化，St 也有波动，但没有发生较大的变化，且各圆柱的St均保持相同。这是由于方形排列的四圆柱的漩涡脱落由再附着模式变为漩涡拍击模式的临界间距比刚好为3.5［9］。因此，各圆柱的St是相等的，这与已有研究观察到的现象相符。

5 结 语

本文采用有限体积法，利用Fluent软件中的RNG κ-ε湍流模型，对临界间距比、不同来流角度下四圆柱的绕流进行数值模拟，通过分析各圆柱的阻力系数和升力系数，主要得到以下结论：

1）随着来流角度的增大，2 号圆柱和3 号圆柱会逐渐摆脱上游圆柱的遮蔽作用，而受到上游圆柱引起的流场变化的作用，这2 个圆柱的阻力系数增大。4 号圆柱仍受到遮蔽作用的影响，其阻力系数偏小。

2）在来流角度增大过程中，升力系数呈现出由离散逐渐收敛的趋势。当间距比为2.0，来流角度为45°时，2 号圆柱和3 号圆柱的升力系数的幅值在图像上表现为关于1 号圆柱和4 号圆柱对称。当间距比为3.5，来流角度为45°时，4 个圆柱的升力系数趋于相等，且与单圆柱的升力系数相近。

3）当间距比为2.0 时，1 号、2 号和3 号圆柱的St均表现为先上升后下降，4 号圆柱的St一直下降。当间距比为3.5 时，各圆柱的St相等，只是随来流角度的变化而略有不同。