基于改进SSA-SVM 光伏板积灰预测及功率影响研究

高 瑜，孔晓龙，王寅清，姜 丰

（西安科技大学 电气与控制工程学院，陕西 西安 710054）

0 引 言

由于中国碳达峰和碳中和目标的提出，给光伏产业的发展带来广阔的前景［1］。在2011年，中国光伏装机容量仅为欧盟的6%，但是从2013年起，国家开始重视节能减排，因此光伏产业得到大力的支持，光伏装机容量在2017年就超过欧盟的总和［2］。伴随着光伏发电的出力占比越来越高，对光伏板发电效率的要求也越来越高，因此灰尘沉积的影响就非常明显。CHEN等通过做多个积灰密度和光伏组件输出功率之间关系的试验发现10 g／m2的灰尘密度使光伏组件输出功率下降34%［3］。陈东兵等通过对蚌埠光伏电站进行数据分析，发现表面灰尘的堆积20天后，使光伏组件的发电功率减少24%，平均每天降低1.2%［4］。JIANG等发现光伏板表面积灰密度如果达到22 g／m2时，电池板发电的效率会降低26%［5］。可见，积灰对光伏组件的发电效率和整体功能有很大影响。

针对光伏板表面的积灰处理主要采用周期性人工清理，但是由于中国的光伏电站主要分布在西北偏远地区并且规模大，每次的清理都会耗费大量的人力物力，所以很需要制定最优的清灰周期。吕玉坤等通过COMSOL软件搭建的光伏模型研究发现在自然状态下，积灰密度到达5.07 g／m2时，输出功率会下降8.71%［6］。KLUGMANN在波兰对光伏组件进行自然积灰试验，发现光伏组件的光电转换效率和积灰量是正相关线性关系［7］。JIANG通过分析积灰速度和密度与光伏组件的输出功率之间的关系，搭建一个估算光伏组件清洗频率的模型［8］。MICHELI调查在美国的20个光伏发电厂，发现小于0.3 mm的降雨对光伏组件是没有清洗效果的［9］。张文帅等对甘肃地区光伏组件积灰情况进行试验研究发现，清理前后的光伏板发电效率能提高8.6%，每天可以多产生7.98 kW·h的电能［10］。从以上的研究结果可见，对积灰进行及时清理是很重要的，所以就需要制定合理清灰周期。

在光伏许多领域的都应用到预测算法。杨旭等利用遗传算法BP神经网络对光伏电站的日污秽损失率进行预测［11］。在先前的研究中分别用Elman神经网络模型、最小二乘法向量机（LSSVM）模型和长短期记忆网络（LSTM）模型对光伏发电功率进行短期预测［12-14］。针对光伏板表面单日的积灰量，提出一种混合改进的麻雀算法（MSSA）优化支持向量机（SVM）的预测方法。通过使用采集到的积灰数据，去测试改进后模型的预测效果，并跟其他的预测模型进行对比。证明改进的模型能够对光伏板表面的积灰量进预测；然后依据积灰量和输出功率之间的关系，分析对功率的影响；再结合降雨量，为清灰工作提供理论依据和数据参考。

1 MSSA-SVM 预测模型

1.1 支持向量机

支持向量机（SVM）是一种基于统计学习理论的机器学习的方法，可以用于数据分类或者数据预测［15-16］。在被用于做回归预测的模型时，可以使用非线性映射函数φ（x），将简单的样本映射到复杂的向量空间上，实现更好地解决小样本的问题。原理为

式中 ω为权值系数；b为偏置项；f（x）表示样本x对应的预测值。

通过运用结构风险最小化原则，将向量回归问题转换为包含约束的优化问题。目标函数以及约束条件分别为

式中 c为惩罚参数，用来表现模型对误差的宽容度；λ＋j，λ-j（j＝1，2，…，n）为松弛变量；yi为真实值；ε为不敏感损失系数。

引入拉格朗日乘子αi，得到SVM回归函数为

SVM中核函数的选取也很重要，合适的和函数能够帮助SVM处理其不能解决的非线性问题。在文中的模型中选用径向基核函数（RBF），如下式

式中 g为核函数的带宽。

在公式（2）中惩罚参数c的选取能反映出模型的泛化能力，其值过大，容易过拟合；反之，就容易出现欠拟合。核函数参数g也对模型的精度有较大影响。为了让模型精度提高，所以就需要用智能算法找到合适的c和g的值。

1.2 基本麻雀算法

麻雀算法（sparrow search algorithm，SSA）［17］是XUE等在2020年提出的智能优化算法，该算法主要由发现者、加入者和侦察者3部分组成，首先是发现者，发现者需要对食物进行寻找，并为种群整体控制觅食方向和区域，占种群数量的20%；然后剩下的是加入者，加入者主要根据发现者提供的方向和区域进行觅食；最后是侦察者，它们种群中随机的10% ～20%，负责在觅食过程中的监视工作［18］。在整个过程中，三者的位置不断更新，最终完成觅食工作。

发现者为整体的种群寻找食物，给加入者提供觅食的方向，如下式

式中 t为当前迭代次数；itermax为最大迭代次数；α为在（0，1］的一个随机数；R2（R2∈［0，1］）和ST（ST∈［0.5，1］）分别表示预警值和安全值；Xi，j为第i个麻雀在第j维中的位置信息；Q为服从正态分布的随机数；L为一个1×d的矩阵，所有元素都是1；d为待优化问题变量的维数；j＝1，2，3，…。

在觅食过程中，部分加入者会不断去观察发现者，倘若发现者找到更好的食物，那么加入者就会跟其进行抢夺。若成功，会立即获得该发现者的食物。加入者的位置更新公式如下

式中 Xp为目前发现者的最优位置；Xworst为当前全局最差位置；A为一个1×d的矩阵，其元素随机赋值为1或-1，并且A＋＝AT（AAT）-1。当i＞n／2时，这表明，适应度值较低的第i个加入者没有获得食物，处于十分饥饿的状态，此时需要飞往其他地方觅食，以获得更多的能量。

警戒者的位置更新公式如下

式中 Xbest为当前的全局最优位置；β为步长控制参数，是服从均值为0，方差为1的正态分布的随机数；K∈［-1，1］为一个随机数；fi为当前个体的适应度值；fb，fw为当前全局最佳和最差适应度值；ε为很小的常数，为了避免分母变成零。

1.3 改进麻雀算法

1.3.1 Logistic-tent混沌映射

利用Logistic-tent混沌映射替代随机生成的方式进行麻雀种群的初始化。常见的主要有Logistic映射和tent映射2种混沌系统，秦秋霞等通过对比分析，指出Logistic-tent映射比常见的2种混沌映射有更好的混沌性能［19］。所以使用Logistic-tent映射生成的种群会有更好的遍历均匀性，于是文中就引入Logistic-tent映射来对初始的种群进行初始化。Logistic-tent映射的数学表达式为

式中 xn＋1∈（0，1）；r为控制参数，r∈（0，4）；Pmin为麻雀位置的最小值；Pmax为麻雀位置的最大值。

通过公式（9）产生的混沌序列Xdim，把Xdim进一步带入到公式（10）中，通过Logistic-tent混沌映射得到新种群Pnew，把得到的新种群Pnew作为SSA算法的初始分布种群，初始种群的多样性和分布的均匀性都会提高很多，最终达到提高算法的全局搜索的能力。

1.3.2 发现者-加入者自适应调整

由于在麻雀算法中发现者和加入者的比例一直不变，导致前期发现者数目不够多，不能进行充分的全局搜索，并且后期加入者数量又不足，不能进行精确搜索。所以文中引入一个自适应调整因子，让发现者数目随着迭代次数的增加缓慢减少，而加入者数目不断增加。让算法逐步从全局搜索转为局部精确搜索，从整体上提高算法的收敛精度［20］。发现者-加入者数目调整公式如下

式中 D为自适应调整因子；FNum为发现者个数；JNum为加入者个数。

1.4 MSSA-SVM 算法优化流程

在预测模型中主要通过MSSA算法对SVM中的惩罚参数c和核函数参数g进行寻优。所以让麻雀个体的位置信息成为一个1行2列矩阵，矩阵的第1行第1列代表c，而第1行第2列代表g。算法运行步骤如下。

步骤1：对SSA的种群数量，最大迭代次数，优化参数个数为2进行设置，设置c和g的取值范围为［0.001，1 000］，选用径向基作为核函数。

步骤2：通过Logistic-tent混沌映射的公式（9）随机初始化麻雀种群的初始位置，使初始种群在参数范围内分布更加均匀。

步骤3：计算每个个体的适应度值及其位置，并开始迭代。

步骤4：根据公式（13）和（14）计算发现者和加入者的数量。

步骤5：根据公式（6）、（7）、（8）分别去更新发现者、加入者和警戒者的位置信息。

步骤6：计算适应度值并且更新种群中最优麻雀位置和最差麻雀位置。

步骤7：判断迭代次数，若不满足条件则重复步骤3到6，若满足，则输出最优麻雀位置，根据最优麻雀位置输出最佳参数c和g，带入预测模型计算。

算法的实现流程如图1所示。

图1 MSSA优化SVM流程Fig.1 Flow chart of SVM optimization by MSSA

2 MSSA-SVM 在光伏积灰预测的应用

2.1 积灰量数据获取方法

为了方便并且准确记录当日的积灰数据，试验采用如图2所示的采集方法，通过用两块表面材料同光伏板一样的玻璃板（200 mm×200 mm，厚度3.2 mm）作为采集板，覆盖在以45°倾角，朝向正南方向的光伏板上，对当天的积灰量进行收集。每天21：00使用高精度电子秤（型号FA2204E，精度0.000 1 g）对玻璃板进行称重。当天积灰量通过用当天称取的玻璃板质量减去前一天记录的数据来得到，然后把当天积灰量除以玻璃板面积得到积灰密度（g／m2），然后把2组数据取平均值。

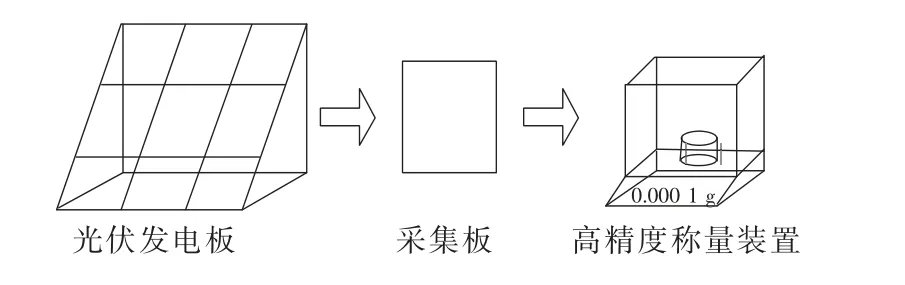
图2 积灰量采集方法Fig.2 Ash accumulation collection method

2.2 积灰数据的选取

为了验证该方法的效果，文中数据是在2022年上半年在陕西省西安市进行的数据采集和记录。收集的数据是从3月份开始到7月份结束。所以该试验没有考虑降雪的因素，但是用到的气象数据均从西安市气象数据系统中提取。由于在收集数据的过程中发现，如果当天降雨量比较大（高于10 mm），会对光伏板表面的积灰进行相对充分地清洗；反之，如果降雨量比较小（低于0.3 mm），会让灰尘的湿度增加，导致积灰量累计急剧变大。由于这2种条件对当日积灰量的影响程度过大，对算法精度也有较大影响，所以把这2种情况归属于极端条件。在对数据进行处理的过程中，对2种极端天气情况进行去除。最终，去除一共11组的极端天气情况。积灰的样本数据就剩142组，然后试验的测试数据，需要在每个月中随机挑选4天的数据组成20组测试数据，用来测试算法的预测效果；剩下的122组作为训练数据，用来构建合适的预测模型。

2.3 仿真效果分析

为了验证提出的改进麻雀算法在积灰预测上有较高精度，文中分别进行灰狼算法、粒子群算法、麻雀算法和改进麻雀算法的仿真运行，并进行仿真效果的对比。

为了直观分析每个算法的训练效果，笔者选用适应度值作为评判训练效果好坏的指标。适应度值的计算采用均方根误差（RMSE）计算公式。因为RMSE能够很好地表现出预测值和真实值之间的偏差，如果它的值越小表示偏差越小，算法精度越高；反之，则精度低。表达式为

式中 m为测试样本的个数；yprei为预测值；yi为真实值。

4种算法的种群数量都设置为50，最大迭代次数设置为100。迭代曲线变化过程如图3所示，可以看出4种算法中GWO算法的收敛速度最慢在第75代时迭代完成，但是改进SSA的收敛速度最快在第32代时就可以找到全局最优值，另外2种算法收敛速度差不多，分别是SSA在第73代时收敛，PSO在第69代时收敛，所以从算法收敛的速度来看MSSA响应的速度更快。然后通过图3中的4种算法适应度值，可以明显看到MSSA算法最后的适应度值比其他的3种算法低，所以说明改进的算法对模型训练效果更好。由此可见在引入Logistic-tent混沌映射和自适应动态因子是能够很好提升算法的收敛速度和精度，进而去提高SVM的预测精度。

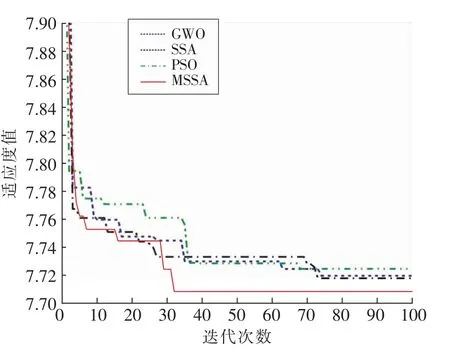
图3 适应度变化曲线Fig.3 Adaptability change curves

为了更加详细和直观地分析对预测数据的预测结果，进一步引入一个拟合度检验系数（R2），因为R2是能够体现算法预测拟合的程度，如果它值越接近1，那么就说明模型的拟合程度就越好；反之，则越差。表达式如下

式中 SSR为回归平方和；SSE为误差平方和；yave为真实值的平均值。

使用4种算法通过训练找到的最优参数c和g，分别带入到SVM预测模型中进行测试，测试结果如图4～7所示，分别为MSSA-SVM，SSA-SVM，GWO-SVM，PSO-SVM模型的预测结果。

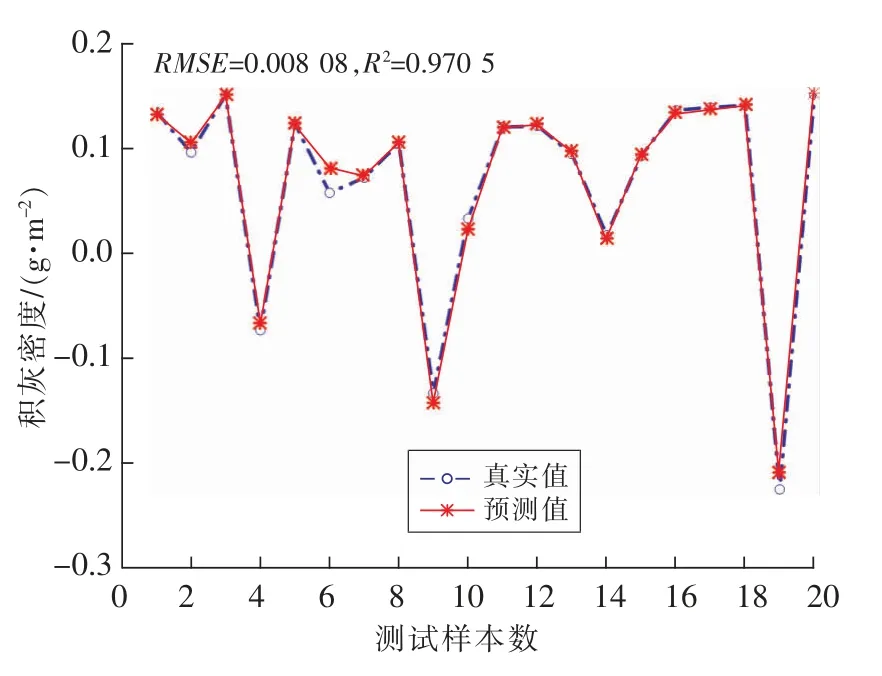
图4 MSSA-SVM预测结果Fig.4 MSSA-SVM prediction results

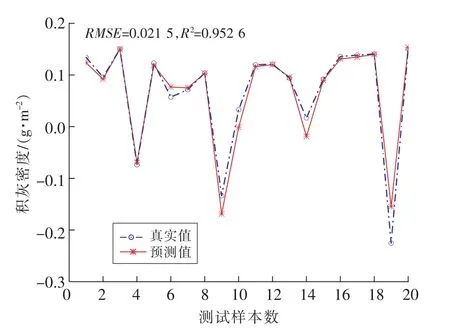
图5 SSA-SVM预测结果Fig.5 SSA-SVM rediction results

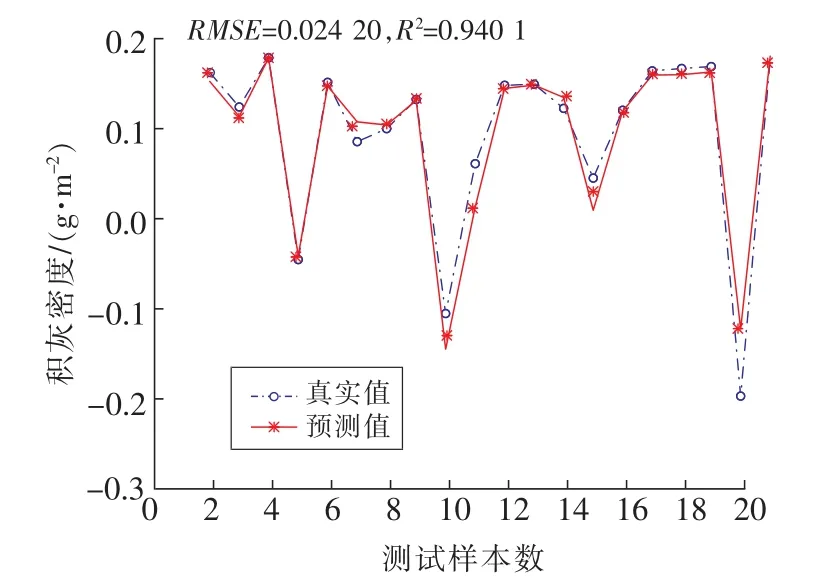
图6 GWO-SVM预测结果Fig.6 GWO-SVM rediction results

图7 PSO-SVM预测结果Fig.7 PSO-SVM rediction results

在对测试集的数据进行运行后，从4种算法的预测结果可见MSSA-SVM的拟合度在这4种算法中表现最好，拟合度达到97.1%；GWO-SVM 和SSA-SVM的拟合度大致相同都在95%左右，而PSO-SVM的拟合度表现较差仅为81.5%。并且从4种算法预测结果的均方根误差可以看出MSSASVM的误差相比于其他3种算法的表现也是最小的，仅为0.008。通过对比分析说明MSSA-SVM预测模型相比于另外3种算法有更好的预测能力，并且精度也更高。它能够通过当天的气象状况进行当日积灰量的预测。

3 积灰影响分析

为了制定合理的清洗周期和给出准确的清洗建议，需要对累计积灰量、降雨量和光伏板输出功率进行综合性对比分析。由于积灰量和光伏板输出功率之间有多种因素影响，所以为了只分析两者之间关系，就假设在辐照度为1 000 W／m2和太阳电池温度25℃时，对光伏板的输出功率和累计积灰量的关系进行分析。通过李练兵等对输出功率的减少率与积灰密度之间的数据进行函数拟合，得出如下拟合函数公式［21］。进而分析累计积灰和输出功率减少率之间的关系，如下式

式中 x为积灰密度，g／m2；y为输出功率的减少率，%。

根据图8和图9统计的数据可以看出，在3月、4月和6月由于降雨天数和量都比较少，所以积灰量比较大，而且在4月25日积灰程度最为严重，达到5.576 5 g／m2，积灰密度每天平均增长0.097 8 g／m2。当天的输出功率的减少率达到13.3%，但是在经过4月26日的强降雨后，表面积灰密度降低到0.011 5 g／m2，输出功率的减少率也降低到0.049%，所以出现超过10mm的降雨时，是可以近似地认为把积灰全部清理。但是，在5月和7月由于有多天降雨，并且降雨量也比较大，所以在这2个月中积灰量和输出功率的减少率都比较低，积灰量最高仅为2.374 6 g／m2，减少率最高仅为10.6%。

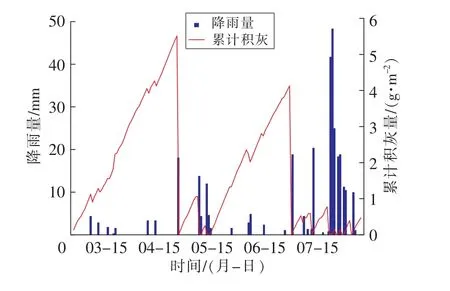
图8 累计积灰量与降雨量关系Fig.8 Relationship between cumulative dust and rainfall

图9 输出功率减少率Fig.9 Reduction rate of output power

通过以上分析可知，如果当天的降雨量达到10 mm以上时，对板面的积灰有很好的清洗效果。所以在降雨量和降雨天数较多的5月和7月，可以减少清洗次数，降低经济投入；反之，在降雨量和降雨天数较少的3月、4月和6月，要及时安排清洗，避免大量的积灰影响光伏出力。

4 结 论

1）提出MSSA-SVM光伏板积灰预测方法。在传统的SSA算法上进行改进，加入Logistic-tent混沌映射和动态变化因子。并搭建MSSA-SVM积灰预测模型，为积灰的预测提出一种新的预测方法。

2）MSSA-SVM 积灰预测模型的预测精度更高。通过和SSA-SVM，GWO-SVM，PSO-SVM 的预测结果进行对比，说明MSSA-SVM模型预测积灰数据误差更小，并且跟实际数据的拟合程度更高。

3）为光伏电站分析光伏板的发电效率和制定清洗计划提供理论依据。通过分析累计积灰量和输出功率减少率之间的关系，能够对光伏板发电效率进行评估；然后，再结合当日的降雨量，来进一步指导光伏板的清洗。