花岗岩强荷载动应力平衡及破裂特征

胡智航，董汉宁，刘 鑫，徐振洋

（1.辽宁科技大学 矿业工程学院，辽宁 鞍山 114051；2.中建一局集团 第二建筑有限公司，北京 102627）

0 引 言

目前，研究材料的动态响应问题常采用霍普金森压杆装置（Split Hopkinson Pressure Bar，SHPB），对波阻抗较高的均质材料而言，应力波在试件内沿加载方向多次传播后，应力应变基本能够达到均匀分布［1］。脆性材料试件往往在很短的加载时间内就发生了破坏，试件两端的应力相差明显，达不到应力平衡状态。对于软材料而言，因试件达到应力平衡所需的时间较长，可能在试件未达到应力均匀以前，加载就已经结束，导致试验结果无效，在获得SHPB试验数据后，必须进行动态力平衡验证，才能保证试验结果的有效性［2］，应力均匀性假定的合理性再次引起人们的关注［3-5］。

近年来，脉冲整形技术已广泛用于工程材料的SHPB测试，有助于研究岩石材料的动力响应特征［6］。FREW 研究组合脉冲整形技术，将铜型整形器与橡胶盘结合，使入射波由矩形波变为半正弦波，以减小入射脉冲的上升斜率［7］。缓慢上升的入射脉冲比陡峭上升的脉冲效果更好，可以最大程度地减小入射脉冲上升沿过程中的波形分散［8］。通过精心设计的加载脉冲，可以使整个动态加载期间实现动态应力平衡［9-10］，实现恒定应变率加载，以克服岩石过早变形失效［11-12］。DONG将脉冲整形技术用于实现动态力平衡，从而消除了负载惯性效应并实现了准静态应力分析［13］。FENG研究发现达到动态力平衡的情况下，尽管惯性载荷最小，但荷载惯性效应最小，并且准静态应力分析仍然有效［14-15］。动态应力平衡发生所需的时间取决于入射波的上升时间［16］。平琦以发现采用变截面入射杆进行加载，能够实现岩石试件在应力峰值之前达到应力平衡，满足应力均匀性假定要求的有效条件，其实质亦是改变加载波形［17］。宫凤强等利用SHPB弹性杆和岩石试件中应力波的反射系数和最小反射次数获得应力差查值表［18］。李夕兵等在SHPB的PFC试验中使用异形冲头，模拟了岩石的变形过程使我们能够测试岩石的峰后行为［19］。但对峰后的应力平衡研究同样对加载波形有着局限性，同时缺少实测数据的对比分析。周子龙在此基础上完善试验，在峰后阶段，尽管岩样已经产生了可见的裂隙但仍能保持很好的应力平衡状态［20］。岩样被劈裂成条状后依然能承受一定的外应力并保持两端的应力平衡。应变率的有效控制，可以改善塑性段测试的应变不均匀性［21］。李夕兵仅针对低应变率岩石动应力平衡过程分析根据应力状态对应力脉冲时间划分［22］。随着岩石应变率的增加，岩石冲击过后的破碎程度、破碎速率增强，都影响着动态应力平衡过程。经过脉冲整形技术后的半正弦加载波，虽然预留充足时间使岩石实现动应力平衡，但其波形特征会加快应力平衡过程中波形劣化现象，应力平衡状态也因此受到影响。

岩石在高应变率作用下的变形特征与破坏强度受微观破坏机制的影响表现为明显的率依赖性，上述研究内容中，对于岩石处于高应变率作用下应力平衡状态变化的研究较少。高应变率加载下，岩石受到动态载荷时，会迅速达到峰值强度然后突然断裂，断裂应变小于1%，在破坏后阶段，岩石变形甚至更快。在应力劣化或失衡前，应力平衡的持续时间是否会影响岩石破碎形态值得深入研究。对一般材料而言，应力均匀性问题主要集中表现在入射加载的前期［21］。采用弹性应力波对岩石应力均匀性等进行研究，具有很强的普遍意义。文中研究了高应变率加载下岩石应力状态的变化及其相应的断裂特征，通过单元模拟确认试验确定的应力-应变演化是否是由于不均匀应力引起的不均匀应变，阐明应变率对应力平衡持续时间的影响，并建立应力平衡时间与岩石破碎之间的关系。

1 试件制备及方案设计

1.1 试件制备及方案

花岗岩试件原材取自河南省信阳矿区，见表1，反射系数λ在-0.55～-0.52，此反射系数范围能获取较好的岩石冲击试验结果并探明其中的科学规律［18］。根据偏光显微镜观察结果，花岗岩主要由45%碱性长石、33%斜长石、18%石英、1%黑云母和3%其他组成。根据国际岩石力学学会的标准，试样端部的平整度和不平行度公差小于0.02 mm。

表1 花岗岩物理力学特性参数Table 1 Physical and mechanical parameters of granite

文献［23］中表明直径为50 mm的均质砂岩试样，在进行SHPB试验时试样长径比λ最小值为0.3。当花岗岩试样长径比大于1.6时，难以达到应力均匀化状态。因此，试验所用地花岗岩试件直径为50 mm，部分花岗岩试样如图1所示，3种长径比λ分别为0.6，1.0，1.4，使应力波在试样内部有足够的传播时间。

图1 花岗岩试样Fig.1 Granite sample

为了确定合适的加载范围，对1.0长径比试件进行冲击测试。当冲击强度低于0.1 MPa时，试件无明显裂隙变形，岩石纵波波速无明显变化。当冲击强度超过0.23 MPa（速度约为14 m／s）时，岩石在单次冲击作用下发生剧烈变形，岩体破碎程度较高且获取应力波传播过程中的有效数据难度较大。因此在完成初步试验后，为了保证结果涵盖范围较全面，确定冲击范围为0.12～0.21 MPa，每次递增0.03 MPa，对应的冲击速度约为8～14 m／s，加载应变率范围在50 s-1～150 s-1。

1.2 SHPB试验原理

根据岩石SHPB试验装置原理，如图2所示，压缩波通过岩石传播，并在岩石内部逐渐衰减。当压缩波首先传播到岩石和荷载杆之间的界面时，由于两者之间波阻抗的差异，压缩波会被折射和反射。此时，岩石两端之间的应力差很大。岩石中的应力波经过多次折射和反射后，岩石两端的应力逐渐增大，应力差逐渐减小，岩石两端应力逐渐叠加至均匀状态，岩石内部达到应力平衡状态。这也是利用SHPB获取岩石动态冲击下有效响应特征数据的假设性前提之一［1］。

图2 SHPB系波的透反射传播Fig.2 Transmission and reflection propagation of SHPB system waves

采用岩石两端应力差值与平均值之比量化SHPB试验中岩石试件应力平衡是目前较好的测量方法［24］。定义试样两端的相对应力差为［25］

式中 k为应力波传播次数；Δσk为岩石两端面应力差值为岩石两端面应力平均值；σk为第k次传播时的应力；ak为相对应力差值。

通常认为岩石两端的相对应力差值ak≤5%时，岩石内部应力近似达到平衡状态［24］。冲击荷载作用下，应力波在岩石内部传播过程中应力分布不均易使应力状态表征出非线性变化。以各级加载应变率下应力平衡持续时间来评价应力平衡过程，采用相对应力差值曲线的波动情况来评价不同应变率加载下的应力均匀性。

MENG研究发现SHPB测试过程中对岩石应力均匀性系数与长径比有关［26］。在应力波上升沿时间内，岩石内部达到应力平衡状态是反映岩石真实动态响应特征的前提。根据应力波传播参数，确定岩石是否能在上升沿前达到应力平衡状态。Δ为应力波单次传播时间，有Δ＝Ls／Cs；k为应力脉冲时间内应力波在试样内部所能传播的次数，属于无量纲参数，k＝［t／Δ］；Cs为花岗岩岩石纵波波速，4 667～5 000 m／s，为了便于计算，取5种长径比花岗岩Cs＝5 000 m／s。0.6，1.0，1.4 3种长径比花岗岩应力波单次传播时间Δ依次为6，10，14μs。

2 应力状态分布

2.1 长径比对应力平衡的影响

如图3所示，12 m／s冲击荷载作用下，当花岗岩试件长径比为0.6时，应力波在传播5次后（第30μs）岩石首次达到应力平衡，随着应力波的持续传播，应力差值曲线波动剧烈，应力波在传播的第5次到第28次期间（第30μs～第168μs），岩石内应力状态反复在平衡与劣化2种分布之间切换，应力波在传播到第17次时，岩石再次达到应力平衡状态并且能维持后续5次传播时长的应力平衡状态，共计30μs；当花岗岩试件长径比为1.0时，应力波在传播8次后（第80μs）岩石首次达到应力平衡；当花岗岩长径比为1.4时，岩石没有达到应力平衡。

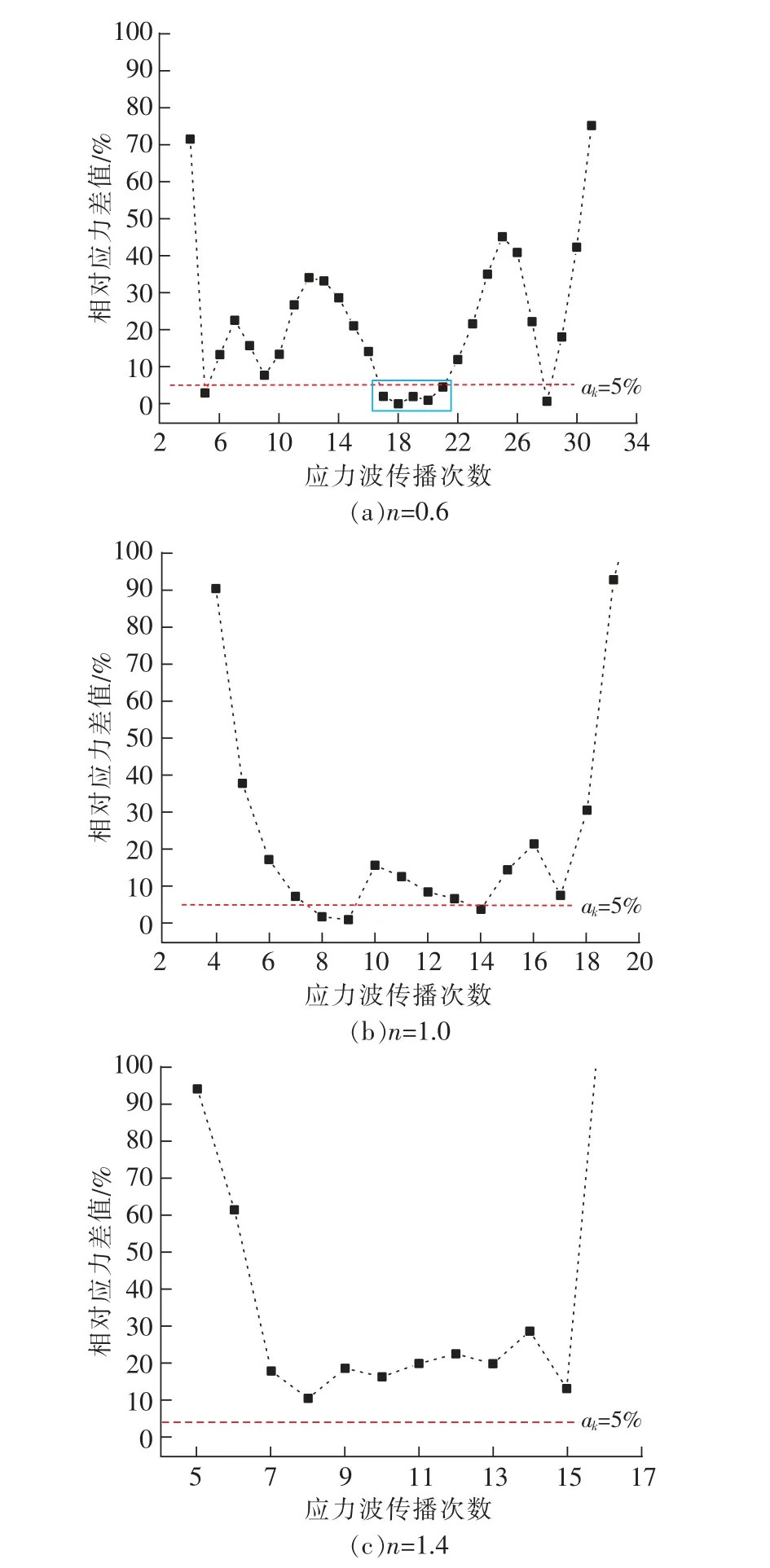
图3 12 m／s冲击速度下不同长径比花岗岩相对应力差值变化Fig.3 Variation of relative stress difference of granite with different aspect ratios under 12 m／s impact velocity

在相同冲击荷载作用下，0.6长径比花岗岩仅在几次传播后便达到应力平衡所要求的相对应力差值，如若不能长时间维持应力平衡状态。当岩石长径比超过1.0后，由于应力波在岩石内单次传播时间较长，使岩石两端的应力差值明显，说明岩石的应力平衡状态不仅与应力波在试样内的传播次数有关系也与试件的长径比有关。试验长径比的变化是改变应力波在岩石内部单次传播时间，应力波单次传播时间越短，达到应力平衡所需的传播次数越多。

2.2 应变率对应力平衡的影响

选用三波法处理数据可以有效的获取真实数据的同时减少人为因素影响的误差。三波法处理岩石材料的应力、应变和应变率的计算见式（4）。

式中 C0，A0和E0分别为SHPB装置压杆的弹性波波速、截面积及弹性模量；ls和As为试样的长度与截面积；εI，εR及εT分别为测得的入射、反射及透射应变；˙ε为加载应变率。

应力脉冲时间内，岩石应力状态波动剧烈的原因是因为，冲击荷载作用下，岩石内部动态应力递增剧烈，当岩石局部因应力集中激活一定数量缺陷，如微裂隙的扩展，使岩石局部发生变形甚至破坏。在动态应力强度未达到峰值前，岩石持续微变形影响着应力平衡状态。

如图4（a）所示，当冲击速度为8～12 m／s时，0.6长径比花岗岩加载应变率处于63.8 s-1～156.8 s-1，岩石在同一时刻达到应力平衡状态，当速度为14 m／s时，岩石加载应变率为253.1 s-1，大幅提升加载应变率使岩石在应力脉冲期间内无法达到应力平衡状态。对比0.6长径比花岗岩在109.8 s-1与160.3 s-12种加载应变率下的应力状态响应特征可知，109.8 s-1加载应变率下花岗岩在传播第8次（第48μs）时首次达到应力平衡状态，随后也出现应力劣化现象，而在第18次传播时（第108μs）时再次达到应力平衡状态且能维持11次应力波传播时长的应力平衡状态，共计66μs。相较于加载应变率为160.3 s-1时，应力平衡持续时间大幅提升了33μs。降低加载应变率虽然延缓了岩石应力平衡完成时间，但可以有效地使花岗岩弹塑性变形时保持应力平衡状态。

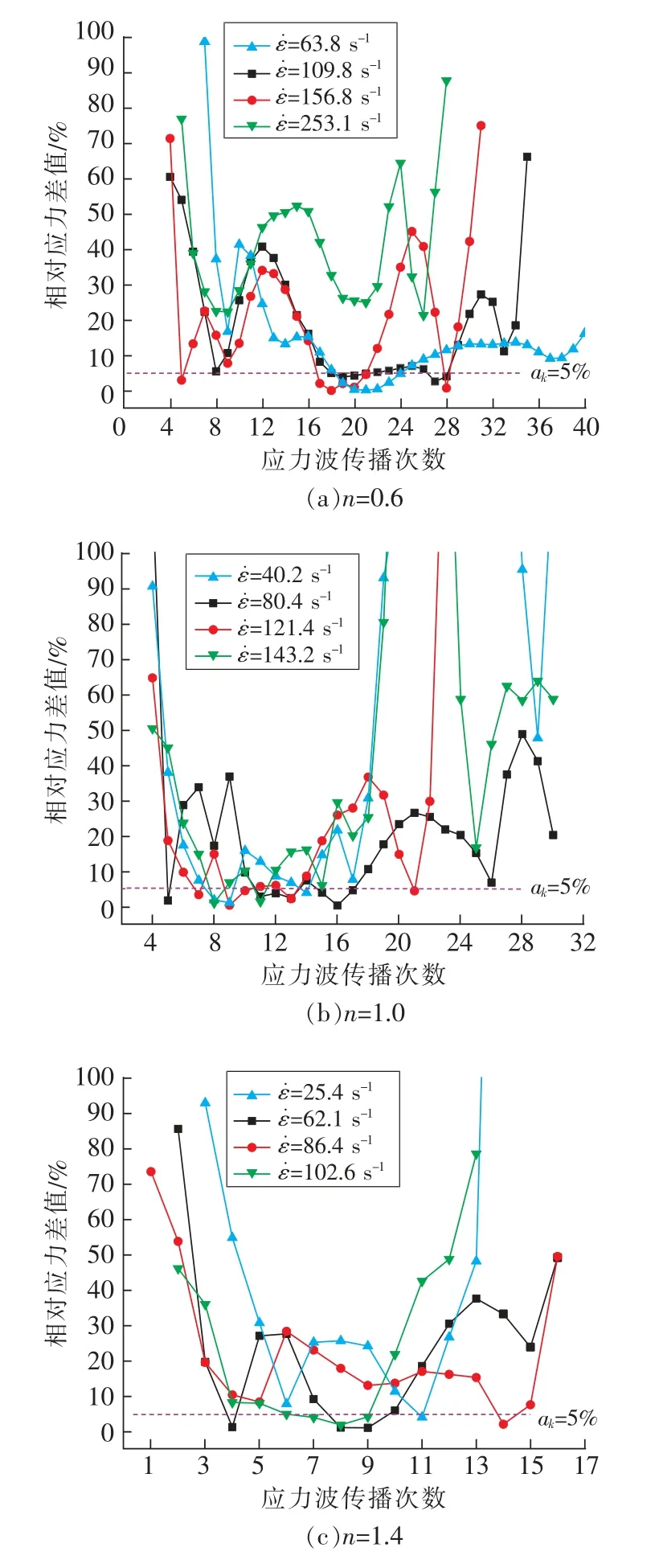
图4 不同应变率加载下3种长径比花岗岩相对应力差值Fig.4 Relative stress difference of three granites with aspect ratios under different strain rates

1.0长径比花岗岩随着冲击速度的提升，岩石的应力平衡变化趋势与0.6长径比一致，在12 m／s冲击速度作用下，即加载应变率为121.4 s-1时，岩石应力平衡状态较好。1.4长径比花岗岩随着冲击速度的提升，应力劣化状态逐渐改善，当冲击速度为14 m／s时，即加载应变率为102.6 s-1时，表现出了较好的应力平衡状态，大长径比岩石提升加载应变率可以有效的提升应力平衡时间，这与0.6小长径比试件应力平衡变化呈现出相反的特性，说明不同长径比岩石存在合理的加载应变率范围，超过其上下阈值，岩石都无法实现动应力平衡。当岩石的加载应变率过小时，应力脉冲携带能量过少，无法均匀的激活岩石的内部缺陷，而当岩石的加载应变率过高时，应力脉冲携带能量过多，使岩石在短时间内形成高应力集中区，岩石提前变形破坏。

2.3 应力平衡持续时间分析

从图5可以看出，0.6长径比花岗岩加载应变率由63.8 s-1增加至156.8 s-1时，应力平衡持续时间呈现出先增加后降低的趋势；1.0长径比花岗岩加载应变率由40.2 s-1增加至143.2 s-1时，岩石应力平衡持续时间呈现出降低的趋势；1.4长径比花岗岩加载应变率由25.4 s-1增加至102.6 s-1时，应力平衡持续时间呈现出先降低后增加的趋势。

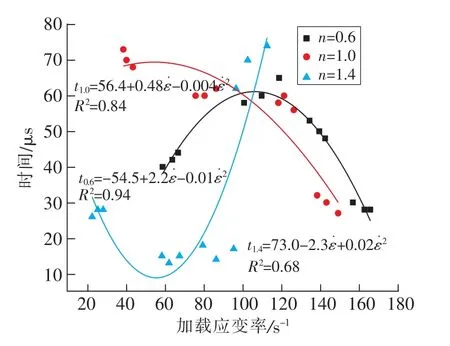
图5 应力平衡持续时间Fig.5 Stress equilibrium duration

从应力平衡持续时长角度来看，0.6，1.0，1.4长径比花岗岩分别在8～10 m／s、10～12 m／s以及12～14 m／s冲击荷载速度下完成了良好的应力平衡，分析认为3种长径比花岗岩在80～120 s-1加载应变率下可以持续长时间的应力平衡状态。

3 高应变率下岩石破坏形态

3.1 破裂特征分析

图6为花岗岩破裂形态，随着应变率的增加，试样的破碎程度呈渐近性增加，且试样的平均破碎尺寸随应变率的增加而减小，表现为明显的率相关性。当试样受单轴压缩时，产生的裂纹沿着平行于压应力方向起裂，并相互贯通形成轴向劈裂，若应变率较高，试样内部微裂纹的激活程度较高，试样呈粉碎性破坏，脆性材料的破碎成形是岩石的率效应机制。

图6 花岗岩试样冲击破碎形态Fig.6 Impact fracture morphology of granite samples

在10 m／s冲击速度作用下，0.6，1.0长径比花岗岩破碎块度相对均匀，而1.4长径比花岗岩破碎后多呈现长条状碎块。结合图5可以发现，0.6，1.0，1.4 3种长径比花岗岩应力平衡持续时间分别为60，60，13μs，对比1.4长径比花岗岩，0.6，1.0长径比花岗岩应力平衡持续时间相对较长，说明随着应力平衡持续时间的缩短，岩石块度从均匀向不均匀转变，应力平衡持续时间的长短决定了破碎后岩石块度分布，影响最终的破碎形态。对比0.6与1.0两者的破碎形态，0.6长径比花岗岩相对均匀，1.0长径比花岗岩破碎块度已呈现出向长条状碎块转变的趋势，两者在相同冲击荷载作用下且应力平衡时间相同的条件下，形成了块度分布差异，是因为岩石的长径比影响着岩石的动态抗压强度，随着长径比的增加，岩石的动态抗压强度增强，0.6与1.0长径比花岗岩在相差近一倍的长度下，破碎块度分布接近，说明岩石应力平衡起到了至关重要的作用。

3.2 应力差值分区研究

通常定义相对应力差值ak越小应力均匀过程越好，而岩石动荷载过程有着尺寸效应以及应变率效应，因此岩石处于劣化状态的破碎也不容忽视，根据上述研究内容，在应力脉冲时间内将相对应力差值分区研究以此来更加准确地表征冲击过程中岩石应力状态变化。

划分区域的界限同样以相对应力差值界定，为了便于研究以10%为步长，研究相对应力差值在0～30%内各长径比岩石状态分布，如图7所示，当相对应力差值超过30%后，岩石两端相对应力差值较大，说明在应力脉冲后期，当相对应力差值超过30%后，岩石已经发生大变形破坏，加载杆端面与岩石端面对接面残缺，加载杆所提供的外部力降低到一定程度，岩石从加载杆两端脱落，相对应力差值快速增幅。

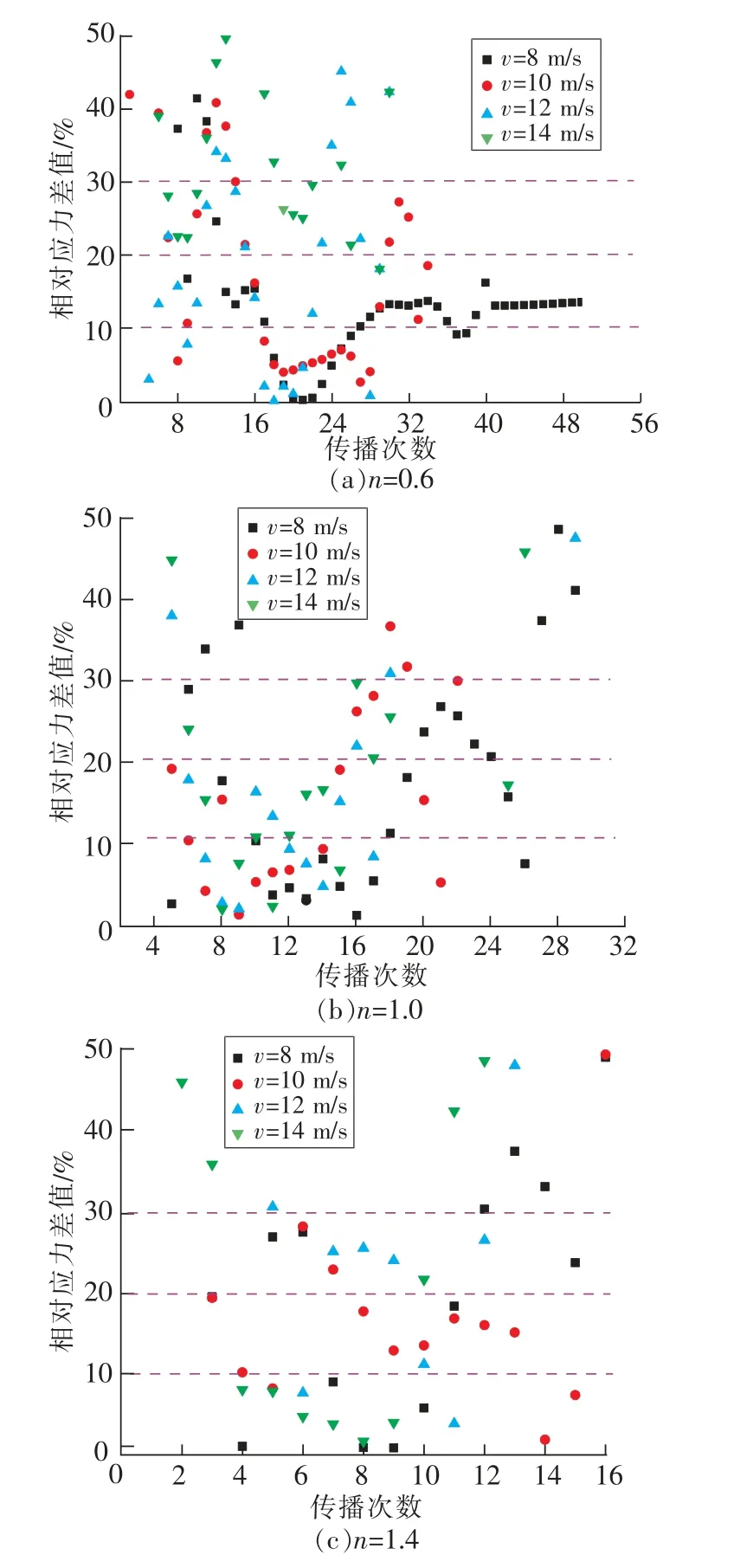
图7 花岗岩相对应力差值分区Fig.7 Stress difference partition of granite samples

岩石的破坏形态主要分为3种：完整型，劈裂型和粉碎型［27］。小应变率加载时，完整型花岗岩处于弹性范畴内加载，该阶段的破坏主要集中于微裂纹的产生，因此应力平衡相对良好；随着加载应变率的提升，花岗岩劈裂型破坏时，应力脉冲时间内，相对应力差值ak大多处于0～10%内，应力平衡持续时间较长，加载应变率增加大幅超过岩石抗载能力阈值后，岩石粉碎型破坏，应力平衡时间大幅降低，相对应力差值ak大多处于10% ～30%内。

从图8可以看出，3种长径比花岗岩在应变率80～120 s-1内时，0～10%应力差值区域持续时间相对较长、10%～20%，20% ～30%两区间内相对较短，其中0.6，1.0长径比花岗岩应力平衡时间的率效应机制表现趋势接近，超过应变率120 s-1后0.6，1.0长径比花岗岩0～10%应力差值区域持续时间大幅缩短，其余区域持续时间大幅增加，而1.4长径比花岗岩表现出相反的趋势，超过120 s-1后岩石的应力平衡持续时间仍在增长，不仅从岩石的应力波传播次数影响应力状态变化，也是与岩石的尺寸效应有关。对比0.6长径比花岗岩，1.4长径比花岗岩随着长度的倍增，其动态强度也随之增加，相同加载应变率下已不满足1.4长径比花岗岩较好的达到应力平衡状态，说明大长径比花岗岩如若想达到应力平衡状态，对加载应变率的需求也更高，而过大的加载应变率会使岩石过早破坏，在考虑应力均匀性假设的前提同时也要考虑应变不均匀性。

图8 不同长径比相对应力差值分区Fig.8 Relative value division of stress difference with different aspect ratios

3.3 应力应变不均匀分析

在此仿真中，该模型使用3D Solid 164单元进行建模，并包含入射杆、传动杆和具有不同接头几何特征的试样。入射杆和传动杆的尺寸与SHPB设备的实际规格相对应，两者都是长度为1 500 mm和直径为50 mm的钢制气缸，试样是长70 mm，直径50 mm的圆柱体，预定义接头的尺寸和形状与实际情况相符，使用六面体映射网格进行生成。在数值模拟试验中，以试样为主要观察对象，可以适当减少为入射和传动杆生成的网格数，以提高计算效率，入射和传输杆的网格单元数量控制在15 000左右，标本的网格可以适当细化，细胞数量可以在260 000个左右，SHPB系统和试样模型如图9所示，在仿真中，加载方法是通过在入射杆的正面馈送半正弦压力波来实现的，半正弦波是从物理试验中获得的入射波转换而来的，更接近实际测试。

图9 SHPB系统与试件的数值模型Fig.9 Numerical model of SHPB systems and samples

在计算过程中，*MAT＿ADD＿EROSION失效准则用于控制单元故障，并通过移除失效单元来演示裂纹扩展过程［29］。选取了1.4长径比试样的有效应力云图和破碎效果，进行分析和说明。

将中高应变率SHPB试验通过ANSYS数值模拟岩石加、卸载过程，研究岩石动荷载应力应变均匀性变化是一种合适的方法，可以观察到岩石加载过程中应力应变全程变化。使用数值模拟软件对花岗岩进行建模、解算，复原花岗岩在冲击荷载作用下的应力应变状态变化。

如图10（b）、图10（c）应力应变云图所示，应力波加载前期，岩石内应力由入射端逐渐向透射端扩展，岩石应变相对均匀；应力波加载中期，单元模型由中部开始最先失效，是由于应力波携带的能量在岩石内部传播时会激活大量微缺陷，同时随着传播距离的增加而衰减，岩石经应力波多次折反射后，中心区域应力均匀叠加速率较快，当中心区域内激活微缺陷达到一定数量后，大量微缺陷紧密衔接，使中部岩石破碎程度较剧烈。在单元失效初期，岩石的应力应变满足均匀性条件；应力波加载后期，模型单元大规模变形失效，使岩石应力分布不均导致应力失衡，这与相对应力差值变化趋势一致，模型变形区域附近应变均匀性较差，而岩石两端应变相对均匀，对比图10（a）1.4长径比花岗岩破碎形态，数值模拟运算结果接近实际情况。

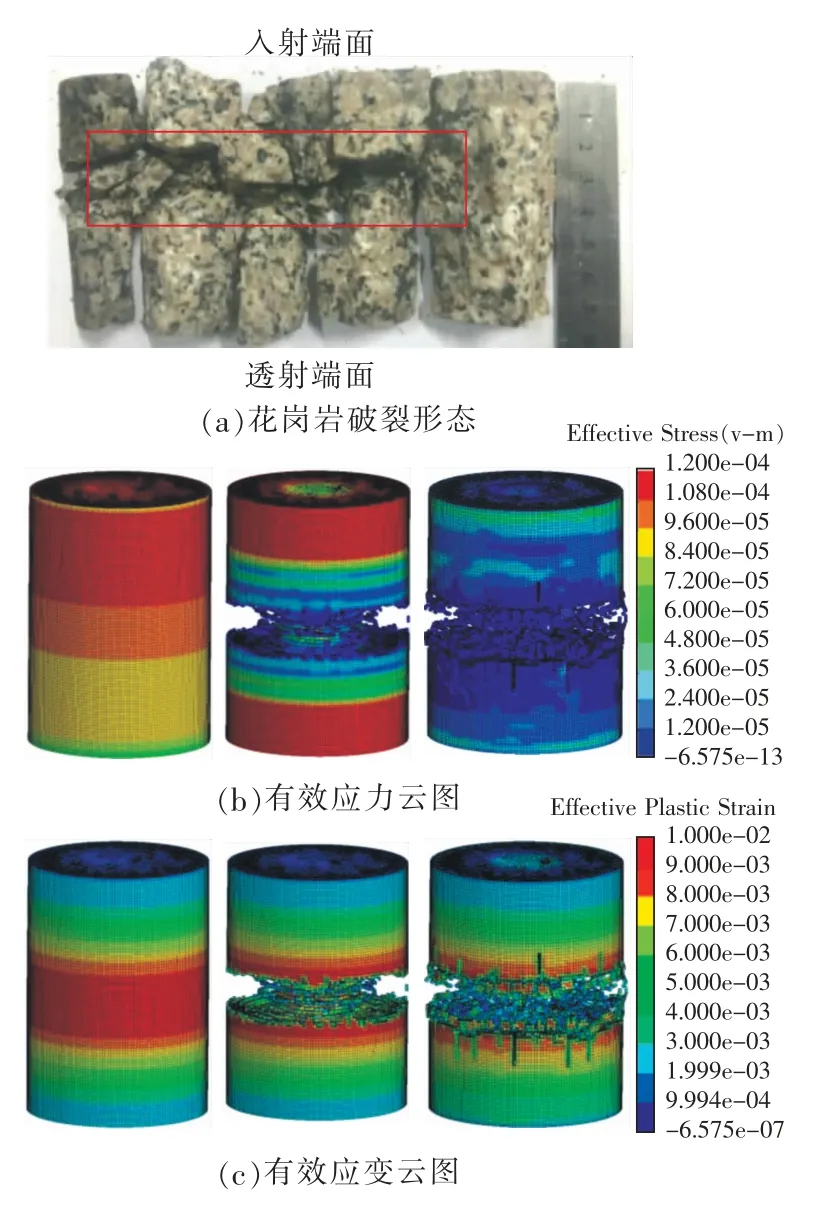
图10 12 m／s冲击速度下花岗岩破碎形态及数值模拟应力应变时程变化Fig.10 Granite fracture shape and numerical simulation stress-strain time history changes under 12 m／s impact velocity

从图10（a）可知，入射端碎块相较于透射端碎块小，是因为在较大冲击速度下的破坏形态，试样与入射杆接触端面的粉碎区域要大于与透射杆接触端面的粉碎区域［28］。应力波携带能量在传播过程中逐渐衰减，大长径比岩石由于单次传播试件较长，岩石两端的应力差仍客观存在，应力分布不均匀使岩石应力集中区发生偏移，造成岩石整体应变不均匀的现象。

结合应力平衡时间结果来看，8～14 m／s冲击速度更适用于小长径比试件加载，当长径比为1.4时，仅在岩石内部形成小范围应力集中。降低岩石长径比从而控制岩石长径比的方式来消除惯性效应可以使岩石达到应力平衡状态的时间缩减，应力平衡状态维持时间延长，使岩石表征出良好应力平衡特性，是满足SHPB应力均匀性假设前提的有效途径。

4 结 论

1）当岩石加载应变率由160.3 s-1降至109.8 s-1时，应力平衡持续时间由66μs降至33μs。降低加载应变率虽然延缓了岩石首次应力平衡，但在应力脉冲总时间内可以有效地使花岗岩长期保持应力平衡状态。

2）高应变率加载使岩石处于应力不均匀状态下破碎，破碎后局部呈现粉碎性，加载应变率˙ε为80 s-1～120 s-1时，1.0长径比花岗岩试样可以在冲击荷载过程中持续保持应力平衡状态。

3）相同冲击荷载作用下，降低岩石长径比可以使应力平衡更易实现，岩石破碎形态由长条状向方块状转变，破碎块度逐渐均匀。

4）弹性阶段岩石满足应力应变均匀性假定，塑性阶段岩石变形破坏应力应变均匀程度下降，过高应变率加载会使岩石应力分布速率加快且不均匀，应力集中处优先形变使岩石应变均匀性骤减，导致岩石形成局部粉碎。