改进的概率秩一判别分析模型及其应用

林慧钗 潘雨婷 滕忠铭

（福建农林大学计算机与信息学院 福建省福州市 350007）

线性判别分析(Linear Discriminant Analysis，简称LDA)[1]是最流行的子空间学习技术之一，是一种有监督的方法，基本思想是将带标签的原始高维样本投影到更低维的空间中，使得投影后的样本类间散列值最大，同时样本的类内散列值最小，使得降维后的样本特征更利于分类。由于LDA 可以有效地捕捉判别信息，因此在分类应用中得到了广泛的应用[2][3][4]。但在大的姿态和光照变化的情况下，大部分的信息会位于噪声较大的子空间中，往往被线性LDA 方法降低权重或者丢弃。因此，Prince 和Elder 提出了概率线性判别分析模型[5]应用于人脸识别上，将人脸数据描述为一个生成模型的结果，结合了个体内部和个体之间的变化，可以提取LDA 可能会丢弃或认为不太重要的判别性特征。但在现实生活中，许多数据自然地组织为张量[6]。尽管 LDA 的有效性已在许多应用中得到证明，但它仅适用于向量，并且在处理多阶张量时必须首先将其输入重塑为向量。因此，为解决此类问题，几种多线性LDA 方法（MLDA）[7][8]被提出，通过利用张量结构，MLDA 学习多线性投影以减少每个方向（即模式）的张量维数。基于散列值比率与差值的MLDA 方法都是有效的，但是他们必须引入额外的调整参数来控制类间和类内散列值之间的权重。从实践的角度来看，这些参数往往很敏感，很难很好地确定。为解决这些局限性，概率秩一判别分析（PRODA）模型[9]被提出，它与PLDA 相似，但以矩阵作为输入数据，提出了一种新的生成模型，将结构信息合并到概率框架中，其中每个观察到的矩阵都表示为集体和个人秩一矩阵的线性组合。使得该模型具有捕获判别特征和非判别噪声的能力，以及利用二维张量结构的能力。但是不论是PLDA 模型还是PRODA 模型都不适用于处理类内方差大的数据，因此I-PLDA 模型[10]基于标准的PLDA 模型，为每类样本引入单独的类内加载矩阵，从而使得新的模型能够适用于类内方差较大的数据集，并在工业数据上获得了更好的故障检测结果。

本文基于PRODA 模型，将模型中的个体参数替换为每类单独的个体参数，建立改进的PRODA 模型（简称I-PRODA）。新模型具有PRODA 模型的优点，且相比较于原模型能够更适用于类内方差大的图像识别分类。

1 模型介绍

为了对PRODA 模型进行扩展，为每类样本引入单独的类内加载矩阵，从而使得新的模型能够适应于类内方差较大的数据集。将第k类数据的第j个样本表示为dc×dr维的矩阵Xjk，j=1,…,Nk，k=1,…,K，因此I-PRODA模型为：

2 参数估计

3 数值实验

3.1 人造数据实验

为了验证I-PRODA 算法在类内方差较大的数据集上具有优越性，构造数据矩阵Xjk,j=1,…,Nk,k=1,…,K，维数为dc=dr=32，5 个类别，每类20 个样本，一共100个样本数据作为训练集，每类10 个样本作为测试集。每个训练集样本数据都根据公式（14）生成：

其中C 和R 的值为0-1 均匀分布的随机数，由MATLAB 合成：

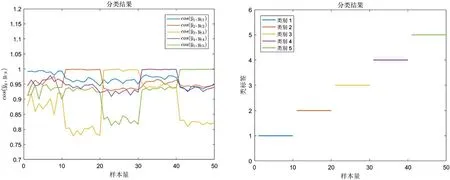
图1： 人造数据分类结果

其中V是添加的噪声，为取值范围在[0,20]的均匀分布随机数所构成的dc×dr维的矩阵。训练集与测试集的数据最后进行标准化，数值范围在[0,1]内。实验的参数初始值为：

3.2 真实数据实验

上一节验证了I-PRODA 算法对类内方差大的数据集有好的分类效果，为验证新算法在实际数据上同样具有优越性，本节使用JAFFE 数据集的人脸图像，将I-PRODA 算法与PRODA 算法进行对比试验。JAFFE 数据集中包含了来自10 个日本女性的213 张人脸图像，每个人的图像含有不同的7 种表情。实验随机抽取每人15 张图像作为训练集，5 张图像作为测试集，即150 个训练集样本和50 个测试集样本，维度都为64×64。在测试集图像中每张图像都在随机位置加入30×30 的方块噪声，所有图像数据都要进行标准化到[0,1]范围内。训练集与测试集的一些图像如图2 所示。

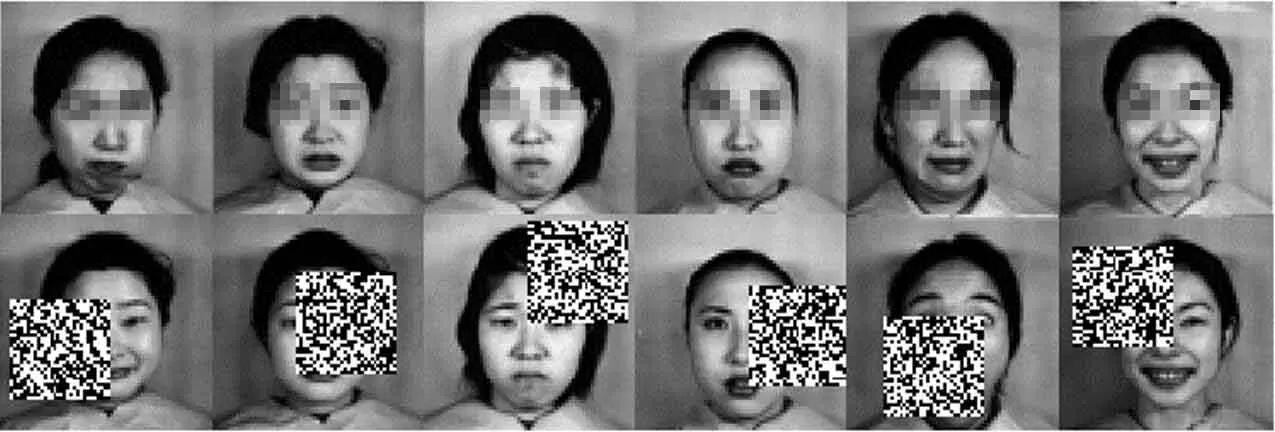
图2： JAFFE 数据集图像

实验结果展示在图3，红色线和蓝色线分别代表的是PRODA 算法与I-PRODA 算法在不同特征维度(py=pz)下的识别率。如图3 所示，2 种算法的识别率都会随着特征维度的增加而升高，I-PRODA 算法对于含有噪声的图像识别要优于PRODA 算法，新算法在特征维度py=pz=40 时，识别率可以达到0.88。综上所述，I-PRODA算法相比于PRODA 算法要更适用于类内方差较大的图像数据集识别。

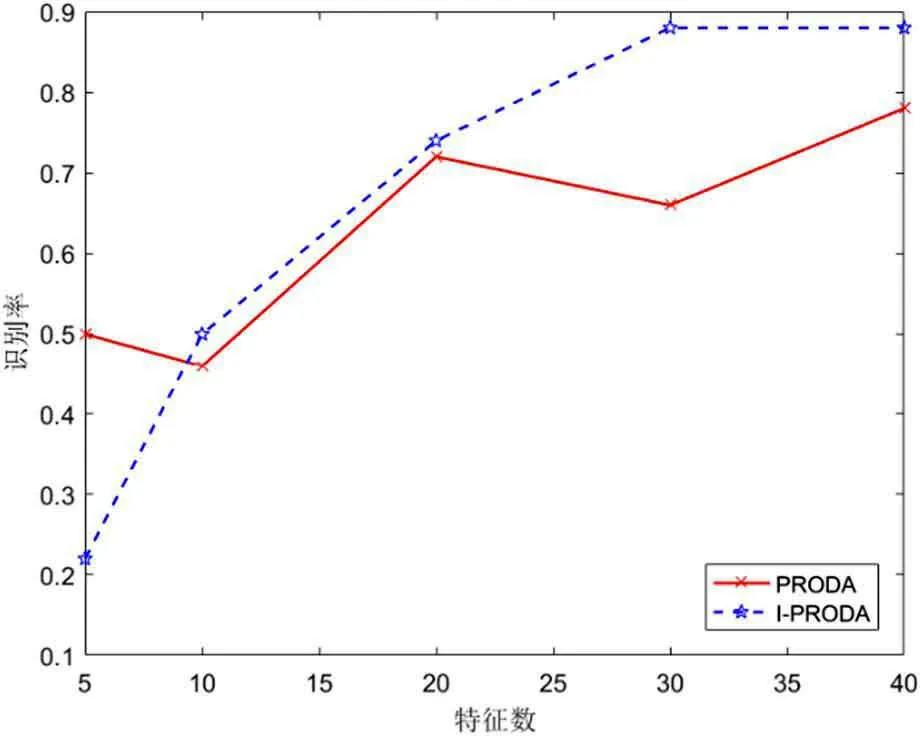
图3： JAFFE 图像识别结果对比

4 总结

本文对PRODA 模型进行拓展，提出了一种改进的PRODA 模型(I-PRODA)，将原模型的个体行列因子矩阵替换为每类单独的行列因子矩阵，使得新模型保留了概率生成模型的优点，能直接对数据进行建模，同时保持数据之间的结构关系，可以更好地利用空间信息；并且相比较于原模型，新模型能更适用于类内方差较大的数据集分类。为验证I-PRODA 模型的优越性，分别进行了在人造数据和真实数据上的数值实验，人造数据实验结果证明新模型能够更好的分类含有噪声的数据，真实数据实验进一步表明了对于含有噪声的图片的识别分类上，I-PRODA 模型的识别效果要优于PRODA 模型。