基于变结构制导律的制导指令校正算法研究
候冰
(成都航空职业技术学院 四川省成都市 610100)
在目前导弹发射的末端过程中,导弹和目标之间的距离相对较近,响应时间非常短暂,而且目标信息也无法精确掌控,因此导致了目标估计量的分析无法做到非常精准[1]。此外由于很多因素的影响,比如噪音、目标不规律机动等因素,导致导弹在飞行期间,面临着各种干扰和影响。因此基于比例制导的古典制导律的制导精度变得越来越低,虽然运用微分对策[2]来提升制导精度也有一定的作用,但是这也是基于目标做大机动的前提,而且这种解决对策也严重依靠模型的分析,所以自身的缺点也非常突出,在实际应用中效果并不好,命中率也并没有得到很大改善。
本文主要是基于变结构系统中的抗干扰的特点[3],来有效的降低打击目标机动性的影响;并且通过在这种变结构系统中的制导回路加入校正环节[4],这样对于导弹弹体的动态反应的延迟都有一定的补偿,从而使得导弹在打击目标的飞行过程中,提高自身系统的机动性,对于打击大机动目标就有了很好的发挥。
1 滑模变结构原理
变结构控制的原理简单来说,是通过控制器的系统反应实现穿越滑模片的调整动作,这样就在一定程度上提升变结构控制的性能,从而达到设计预期效果[5]。因此,采用变结构控制系统的作用就非常突出,且意义非常重要。它的控制灵敏性、适应性都有了极大的提高,而且系统的适应性更强,相比经典控制线性化,其动态以及静态性能让人满意,和一般的固定结构相比更为灵活。
结构控制理论诞生在上世纪的五十年代末期,通过将近二十年的不断研究,美国、欧洲等科学家对于变结构的理论有了新的认识,并且也取得了一定的研究成果。其中最显著的就是将其理论研究的非常透彻,而且科学家们已经认识到了非线性系统具有很强的发展前景[6],其特性都非常突出,尤其是在应用在具有系统摄动以及外部扰动的实践中,非线性系统能够发挥更大的价值。所以对于变结构控制的研究更是投入了巨额的精力,也取得了很大的成就。当前人们对变结构控制理论的特性认知为以下几种:
1.1 模型降阶
在基于滑动模态环境中,系统的估计运动实际上已经被局限在低阶子环境中,这时系统运动就可以通过数学微分方程构建。当然,实际上滑动模态是在m 维切换平面的空间上,因此,就可以通过低阶m 的n-m 阶滑模方程来表述系统特性[7]。
1.2 系统解耦
在变结构控制体系中,系统状态和切画面的选择有直接的关系,这样就可以有效实现系统解耦。
1.3 鲁棒性特点
在变结构控制中,具有很强的系统数摄动的抗干扰能力,这种能力也通过三十年的不断研究,从而在实践中取得了很大的成果,目前在很多工程领域中,都有其原理的应用。
1.4 性能卓越,便于实现
变结构具有性能优良的动态、静态特性。所以在具体的实现中相对容易。
1.5 振动
在变结构控制中,会有很多影响因素,包括时间延迟以及系统惯性影响因素,所以也导致了滑模面在趋近状态中的远点,要想实现滑模运动几乎不可能。而在实际的系统应用中,系统的状态也确实是不够稳定,比如在穿越滑模面时,就会出现不停的振动,这和人们预期的朝滑模面滑动是有很大的误差的。当然这种振动其实来自于导弹本身的振动,尤其在导弹这种细长的物体中,振动就会导致导弹本身的弹体出现高频剧烈的振动,这样就不能体现出良好的动力学性能,而且由于导弹弹体的不断振动,对于有效控制的实现难度也变得非常大[8]。所以在当前的变结构系统研究中,振动是必须要尽快解决的一大难题。
2 制导算法设计
2.1 系统模型建立
首先要进行的就是系统模型的建立,这也是整个算法设计的基础。具体先以视线坐标系将目标和导弹之间的相对运动过程以参考坐标系的方式表示出来。在坐标系中Y 轴表示的是导弹运动的上方;X 轴表示的是末端制导开始的时刻的视线方向,X 轴和Y 轴相互垂直。如图1 所示就是在建立起来的坐标系中目标同导弹之间在几何平面上的关系。将导弹的弹道倾角、前置角、速度分别定义为θM、ηM以及VM;将目标的速度方向角、前置角以及速度分别定义为θT、ηT以及VT;而导弹同目标之间的视线角度以及相对距离则分别用参数q 和R 来进行表示。
建立导弹-目标相对运动模型:
在上面的运动模型之中将距离变化量以及视线角速度分别定为 和。同样的根据假设条件:
(1)目标以及导弹都以质点的形式运动;
(2)目标的加速度有上限的a,并且目标的加速度aT小于最大上限,即为|aT|<a。
(3)导弹的速度VM比目标的速度VT要大,并且两者均为常数。
2.2 算法设计
在本文的制导率设计的过程中引入了变结构控制理论。从文献[23]中选取变结构制导律如下:
式中:ac为加速度指令,k为比例项导引系数,R为弹目相对距离,q为视线角速度,Ω 为大于零的待定正数。
其中饱和函数:
式中:δ>0 是由仿真确定的常数。
该制导算法未考虑目标机动和控制系统动力学影响,故本文将目标机动视为未知的有界干扰,然后为了消除和减小目标机动所带来的影响,在算法之中运用了变结构控制系统具有干扰不变的这一特性。
首先,将开关平面进行确定,即:
为了方便计算,需要将目标在做出有界机动的时候的视线角速度 变为零,这时制导律就派上用场了。而系统需要能够在一定时间内有效命中选择的开关平面,所以选择变结构控制使得 在这一时间限定范围内变为零。

导弹变结构制导系统结构如图2 所示。
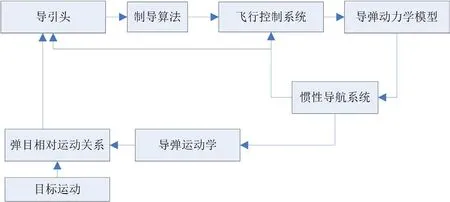
图2: 导弹制导回路框图
接着将上面得出的系统进行简化,使之成为非线性反馈通路以及线性的前向通路。在经过简化后得出了如图3 所示的回路。在这个回路中非线性环节就是ac,这也是回路中的非线性环节;而运动学、弹体以及导引头这些线性前向通路则为其中的W(s)。
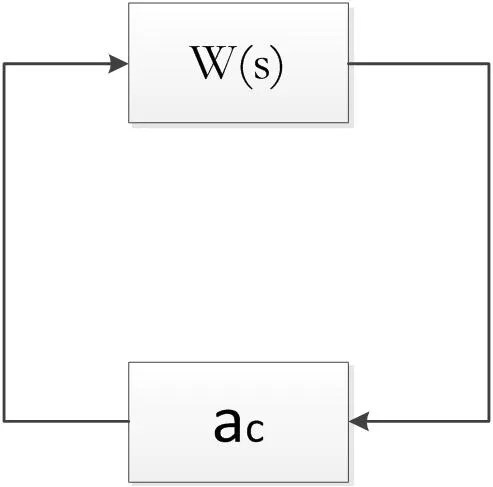
图3: 简化后的制导回路模型
其中:τ为导引头时间常数,Td为弹体响应时间常数,ζ为阻尼系数。
此时在制导回路中引入校正环节,从而将控制加速度aC计算出来,在将其与图4 中的制导控制回路相互结合带入计算,最终就能够得出导弹的加速度aM。依然考虑在图4 中引入前馈和反馈单元,通过超前环节和比例环节改善系统的动态性能,对控制系统存在的延迟进行补偿。这里一个包含前馈信号G4(D)ac和反馈信号G3(D)(ac-aM)的新的加速度指令aA如下:
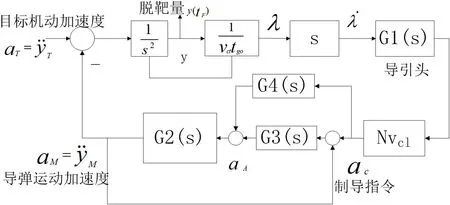
图4: 引入指令校正的制导回路模型
式中,D 是微分算子,传递函数G3(s)和G4(s)分别表现了前馈和反馈通道的特性。
传递函数W∑(s)表现了ac和aM的输入输出关系,其表达式如下:

式中τ10、τ20和k1都是常数,μ=1 或0,k2=1 或0。

确定具体参数的时候,要从稳定性、快速响应能力和制导精度(即脱靶量)三方面综合考虑,在制导性能得到提高的同时对制导回路不造成较大负面影响。
2.3 系统稳定性分析
在传统的频域分析方法具有许多的局限性,因此无法对基于变结构制导律的非线性特性的稳定性进行系统和准确的评估分析。为了解决这一问题,在系统的稳定性分析之中另外引入了圆判据,这一判定方式可以看成是奈氏判据的进一步拓展。
圆判据的过程简而言之,即利用1 个表征扇形域K(k10,k20) 的圆来替代掉在奈氏判据中的点(-1,j0)或者是点(-1/K,j0)。在线性条件下判定非线性系统绝对稳定性的时候一般是通过计算频率特性W(jω)绕点(-1,j0)转的圈数得出的,而在这里则使用W(jω)围绕圆判据中圆的圈数来进行得出的,这两者之间的原理上是相通的。接下来即依照这一圆判据来进行具体的分析过程:
在之前得出的公式(3)中得出了变结构制导律中的非线性部分是q/(|q|+δ),而在这里则取一个具体的值δ=0.01,然后即可得出圆判据中的扇形域是K[0,k20]。
首先考虑G3(s)=k1的情况。通过选择合适的k1,比如k1=3,可以明显减小e=ac-aM(使ac逼近aM)。W∑(iω)的实现有两种途径:k1=3,k2=0 和k2=1。
由圆判据理论可以知道,要想一个系统处于稳定状态,参照k20>k10=0 时的具体过程,就必须使得其频率特性奈氏曲线在直线U=-1/k20的右边。在对具体的过程进行深入分析之后可以得出当U=0 是一个虚轴的时候,k20变为无限大。然后再将前面回路中的频率特性奈氏曲线绘制出来,对其进行分析后即可得出系统的稳定性状况。
具体的分析过程是以500m 以及1000m 的相对弹目距离R 的值来分别进行迎击的典型攻击条件的仿真分析,然后得出如图5 的频率特性。
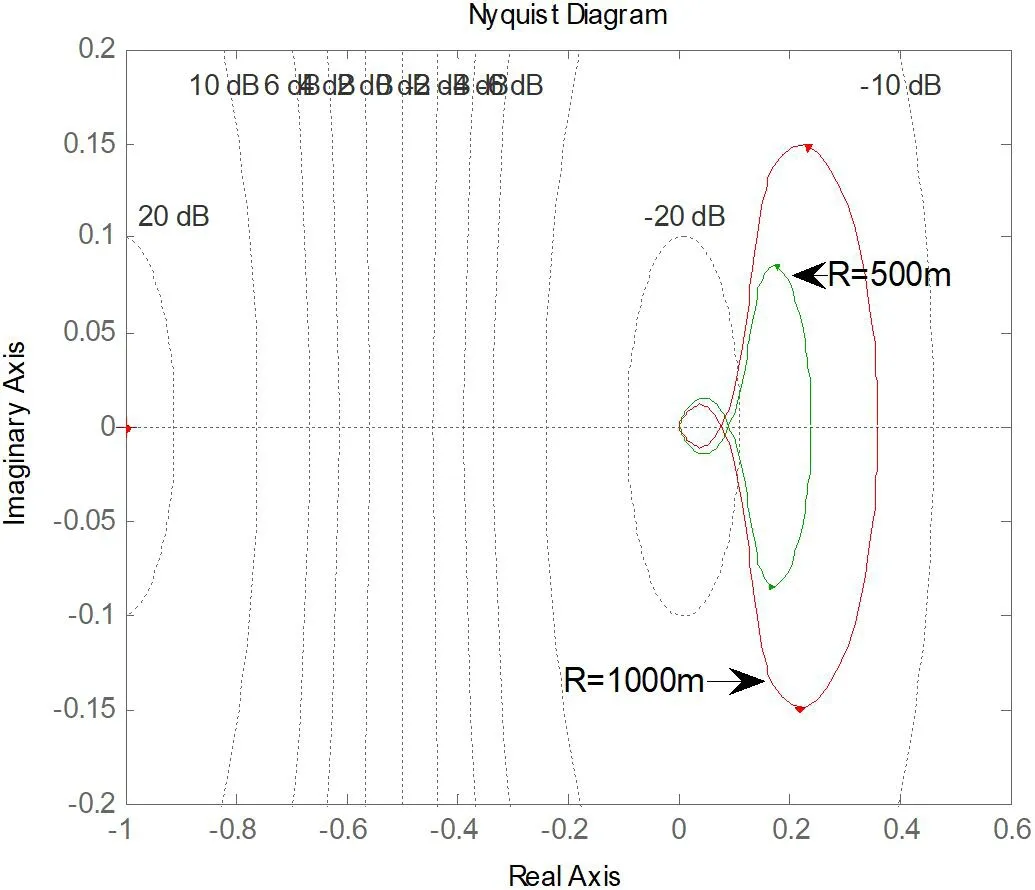
图5: 相对距离R 分别为1000m 和500m 时的频率特性
在变结构制导算法的计算过程中坐标系的虚轴即为直线U=-1/k20=0,而非线性的部分则为k20=+∞。依照圆判据的具体内容,依照在上图5 相对距离R 分别为1000m 和500m 时的频率特性即可得出制导系统在这两个R 值的情况下均处于稳定状态。
总的来说,将指令校正引入到变结构制导算法使其稳定性变得非常强。但是在需要考虑的是在实际过程中直线U=-1/k20≠0,即其不是一个真正意义上的虚轴,这是因为δ=0.01 的情况下不能够被忽略。但是从分析得到的结果来看,经由这一结合算法得出的制导回路的稳定性总体上表现良好。
3 仿真验证
为了保障本文设计的变结构制导算法能够更好的运用于实践中,接下来进行在弹道末端目标大机动逃逸方式下的数字仿真测试过程。在这一过程中没有像传统方式一样对未引入指令校正和引入指令校正控制导弹的飞行状况进行对比分析。令,进行仿真分析。
如图6-图8 所示,从仿真结果的对比分析可以看出,目标大机动时,比例制导算法视线角速度以及法向加速度在末端会发散,而引入指令校正的变结构制导算法依旧可以保持良好的收敛特性;同时脱靶量要小于比例制导算法。相对于比例导引律,引入指令校正且结合了变结构制导律来提高系统的稳定性,进而使得系统制导精度得到有效保障。
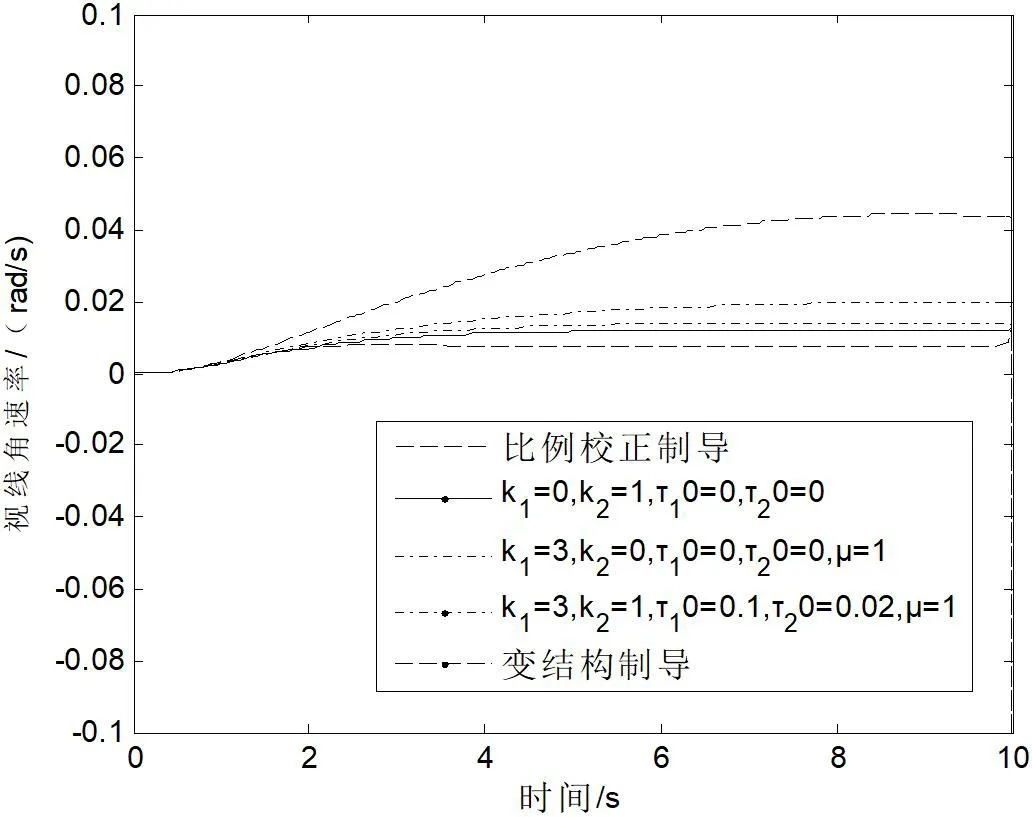
图6: 视线角速度变化曲线

图7: 法向加速度变化曲线
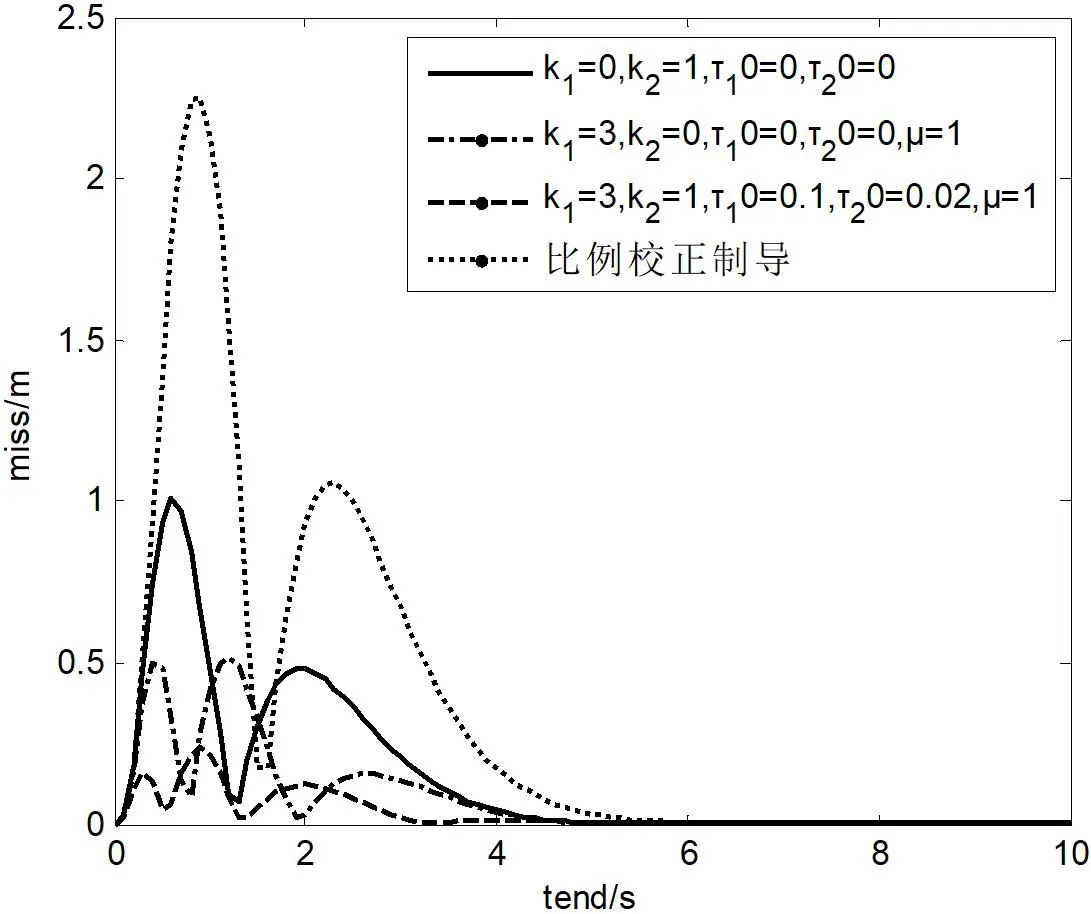
图8: 脱靶量变化曲线(其中变结构制导曲线因与实线重合,没有标注)
在目标处于机动状态且较大的情况下,比例导引算法则存在着很大缺陷,因为其本身的假设前提就是目标一直处于匀速直线运动的状态。这也是为什么本文选择了变结构制导算法的原因。在变结构制导算法之中考虑了目标的机动状态,通过对变结构项的系数进行具体的设定,并且将目标的速度作为输入量带入到计算过程,这样就使得系统很好的应对大机动目标。同时为了满足面对机动目标的高命中率,引入了指令校正,使得制导系统的制导精度得到很大提高。指令校正的引入同时也使得系统的控制具有快速响应的特点,很好的增强了系统的鲁棒性。
4 结论
本文基于变结构制导律的制导指令校正算法进行研究,概述了变结构控制理论的基本概念、抖振产生的缘由以及消除方式,同时还设计了切换函数、对控制系统的性能以及滑模变结构控制系统的设计进行了理论上的详细分析。依照变结构理论的具体内容,结合考虑实际过程中目标机动影响因素,设计出这一理论下具有干扰不变特性的变结构导律来减小和消除其带来的影响;同时在制导回路中引入指令校正环节,以改善导弹制导性能。基于变结构制导律的非线性特性,对制导回路的分析采用圆判据方法。仿真结果显示,该新型制导算法在攻击大机动目标时抗干扰性和鲁棒性更好。

