二水平正规设计中主效应的混杂性质*

米乃瓦尔·亚森，李智明

(新疆大学 数学与系统科学学院，新疆 乌鲁木齐 830017)

0 引言

试验设计特别是二水平正规设计在科学研究的各个领域中备受关注.文献[1]认为一个试验往往有多个设计方案, 试验者如何从中选择最优设计是研究中的难点问题.研究者给出一些准则下的最优设计, 如最大分辨度准则[2]、最小低阶混杂准则[3]、纯净效应[4]等.这些准则都基于效应排序原则: 低阶效应比高阶效应重要;同阶效应同等重要, 它们从不同角度反映了一个设计中不同因子之间的混杂程度.一个2n－m正规设计D由n个因子F1,F2,···,Fn组成, 共N = 2n－m次试验.每个因子都是二个水平, 用+1和-1表示.在因子F1,F2,···,Fn中,有n-m个独立列, m个额外列(称为定义字).这m个定义字生成的子群称为定义对照子群G.令Ai为定义对照子群G中字长为i(i=1,2,···,n)的字母个数, 称序列W =(A1,A2,A3,···,An)为设计的字长型(WLP).文献[3]通过顺序最小化WLP中元素选择最优设计.文献[5]提出二水平正规设计的别名效应数型来描述所有因子之间的混杂信息, 得到字长型对应于别名效应数型中某些元素的函数, 并在别名效应数型的基础上提出了一般最小低阶混杂准则.文献[6]计算了别名效应数型中的主要元素.有关二水平一般最小低阶混杂准则的理论性质及设计构造可参阅文献[7-13].

在最优设计的选择上, 主效应和各阶交互效应的混杂情况往往更为重要.为了更好地描述主效应与各阶因子交互效应混杂的情况,文献[14]在某些二因子交互效应重要的先验情况下,根据线性模型的最小二乘估计提出了描述主效应与各阶因子交互效应混杂的别名矩阵,并引入混杂指标集来选择最优设计.但是,对于该指标集的性质及计算相关研究较少.本文主要通过别名矩阵及别名效应数型来计算混杂指标集中的重要元素.

1 基本概念

令q=n-m及N =2q.对于一个2n－m正规设计D, 若考虑主效应与其它高阶效应之间的混杂结构, 根据文献[15]建立一个线性模型:

称之为基于主效应的别名效应数型(Aliased Effect-Number Pattern Based on Main Effect, 记M-AENP).顺序最大化式(6)得到设计称之为基于主效应的一般最小低阶混杂(General Minimum Lower-Order Confounding Based on Main Effects)设计, 简记为M-GMC设计.

例1 考虑两个非同构的212－7设计

由(6)式可得

根据混杂指标集定义, 可计算

2 主要结果

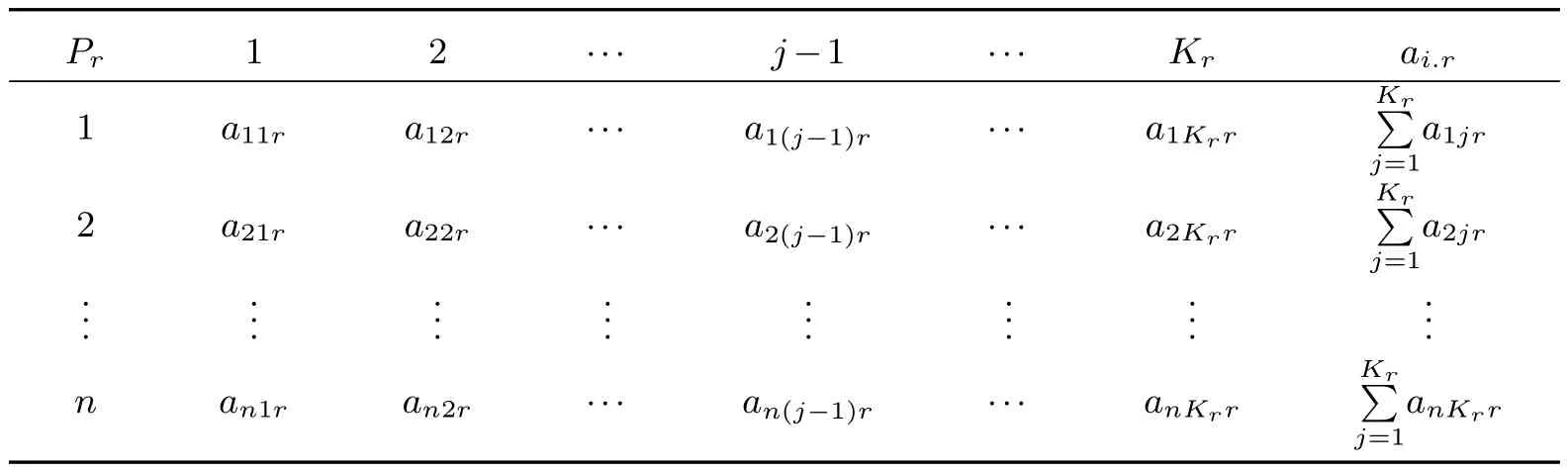
表1 2n－m正规设计的r阶别名矩阵Pr

由矩阵Pr可知, ai.r可能取值分别为0,1,2,···,Kr.令mlr表示ai.r取某一数值对应的频数, 见表2.

表2 ai.r取值的频数分布

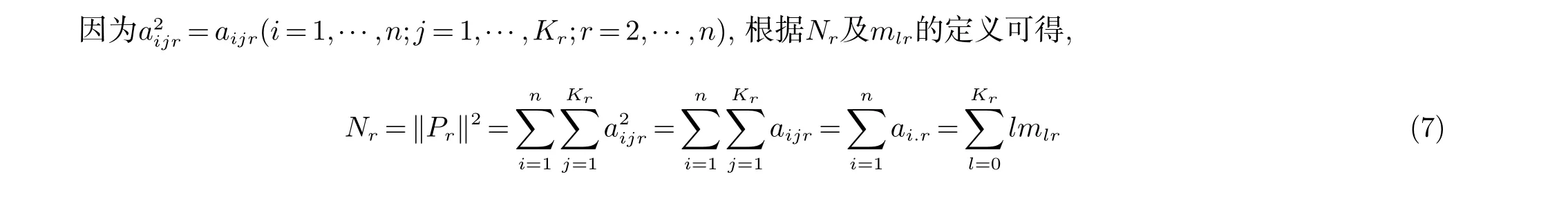
根据(7)式直接可得以下等价性质.

定理1 最小序列化N=(N2,···,Nn)等价于最小序列化

其中: l=0,1,···,Kr;r=2,···,n.根据(8)式得到

根据式(9), 可以得到最小序列化N=(N2,···,Nn)的另一个等价定义.

定理2 最小序列化N=(N2,···,Nn)等价于最小序列化

定理1揭示了混杂指标集N与别名矩阵Pr之间的关系, 定理2反映了N与基于主效应的别名效应数型之间的关系.

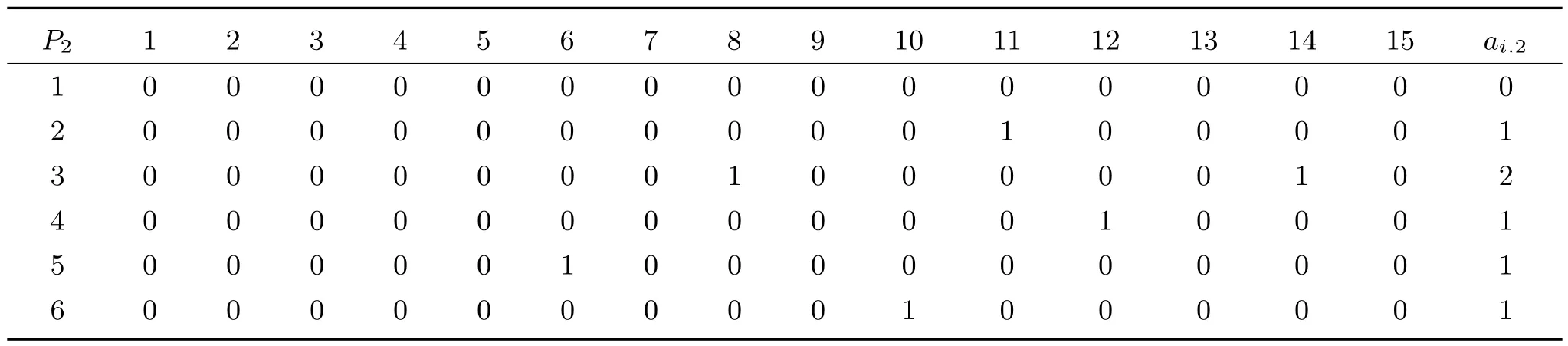
表3 二阶别名矩阵P2

由式(9)和式(10～12)得

由文献[17]可以给出

3 部分最优设计表格

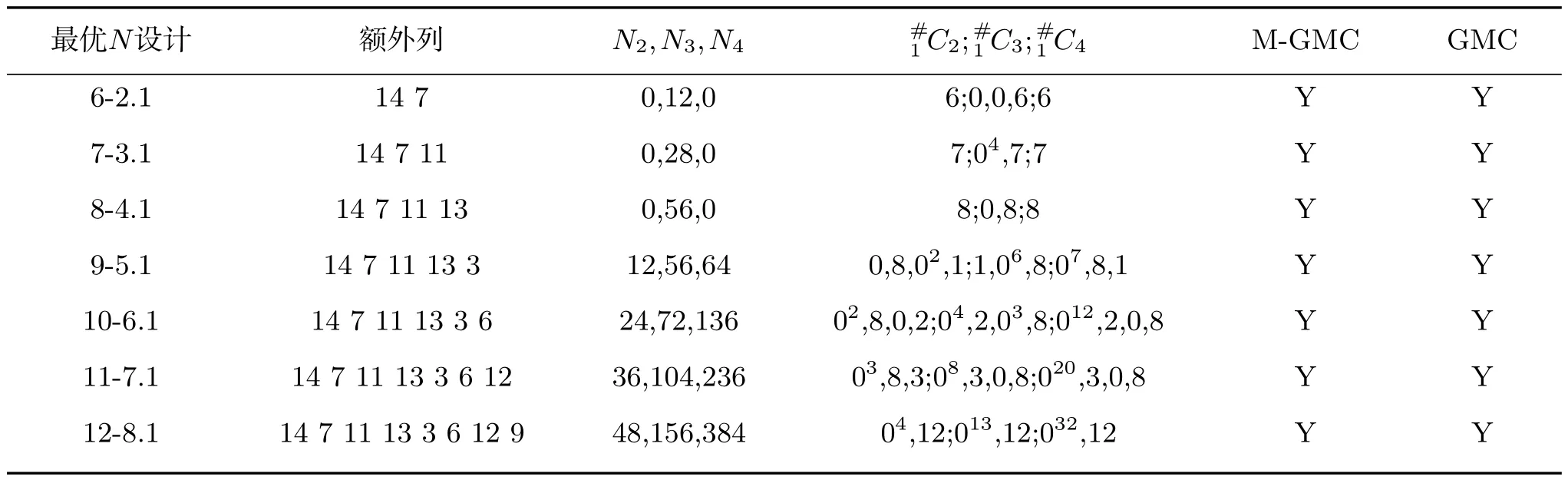
表4 16次试验的二水平设计

由表5可知, 当n=7,8,10,13,···,19以及n=22,23,···,28时, 试验次数为32次的最优N设计既是M-GMC设计又是GMC设计.212－7,220－15,221－16最优N设计是M-GMC设计但不是GMC设计.29－4,211－6最优N设计既不是MGMC设计也不是GMC设计.

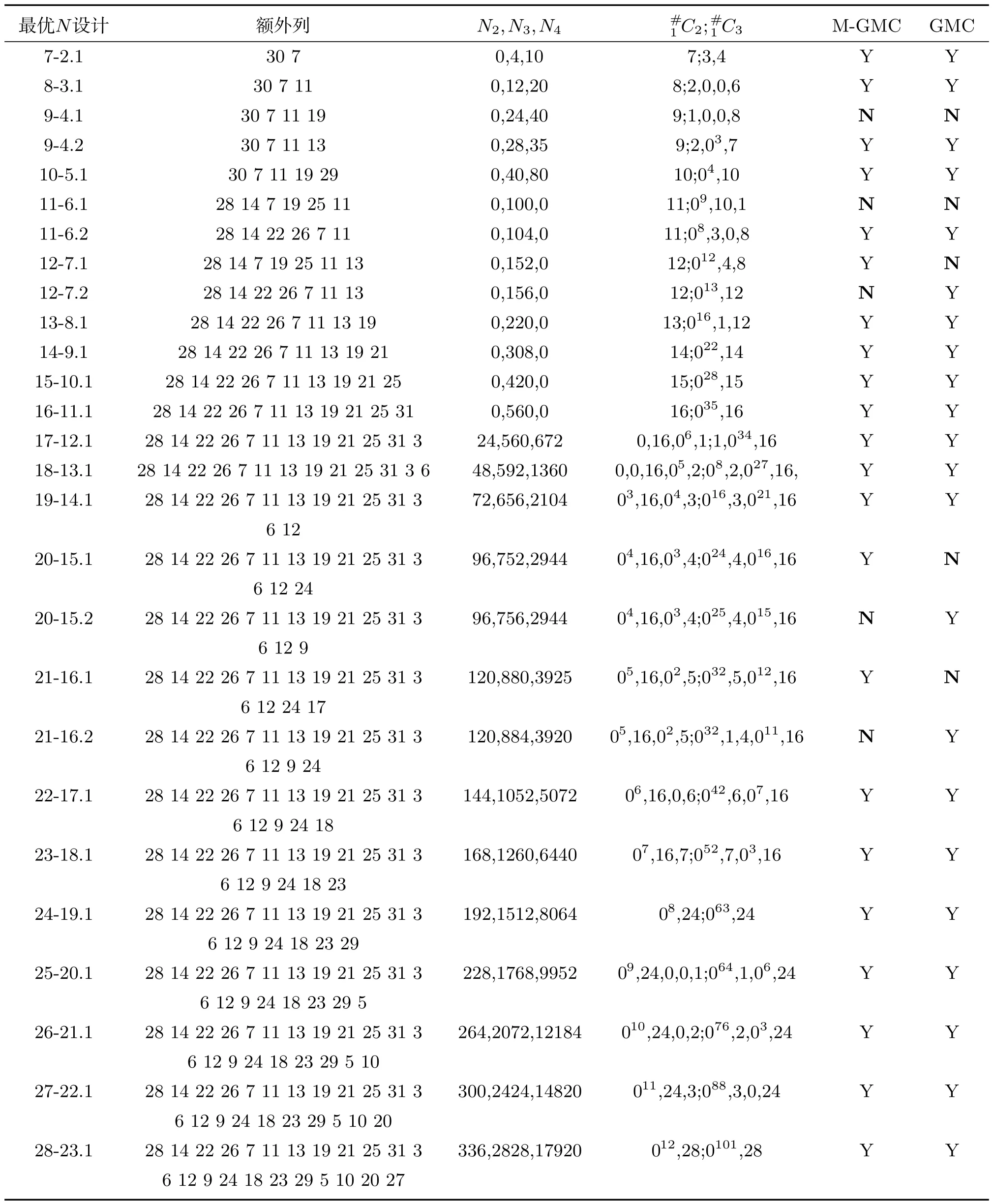
表5 32次试验的二水平设计

由表6可知, 当n=8,···,12,19,20,29,30,31,32时, 试验次数为64的最优N设计既是M-GMC设计又是GMC设计.223－17,224－18,228－22最优N设计是M-GMC设计但不是GMC设计.当n=13,···,18,21,22,25,26,27时,最优N设计既不是M-GMC设计也不是GMC设计.

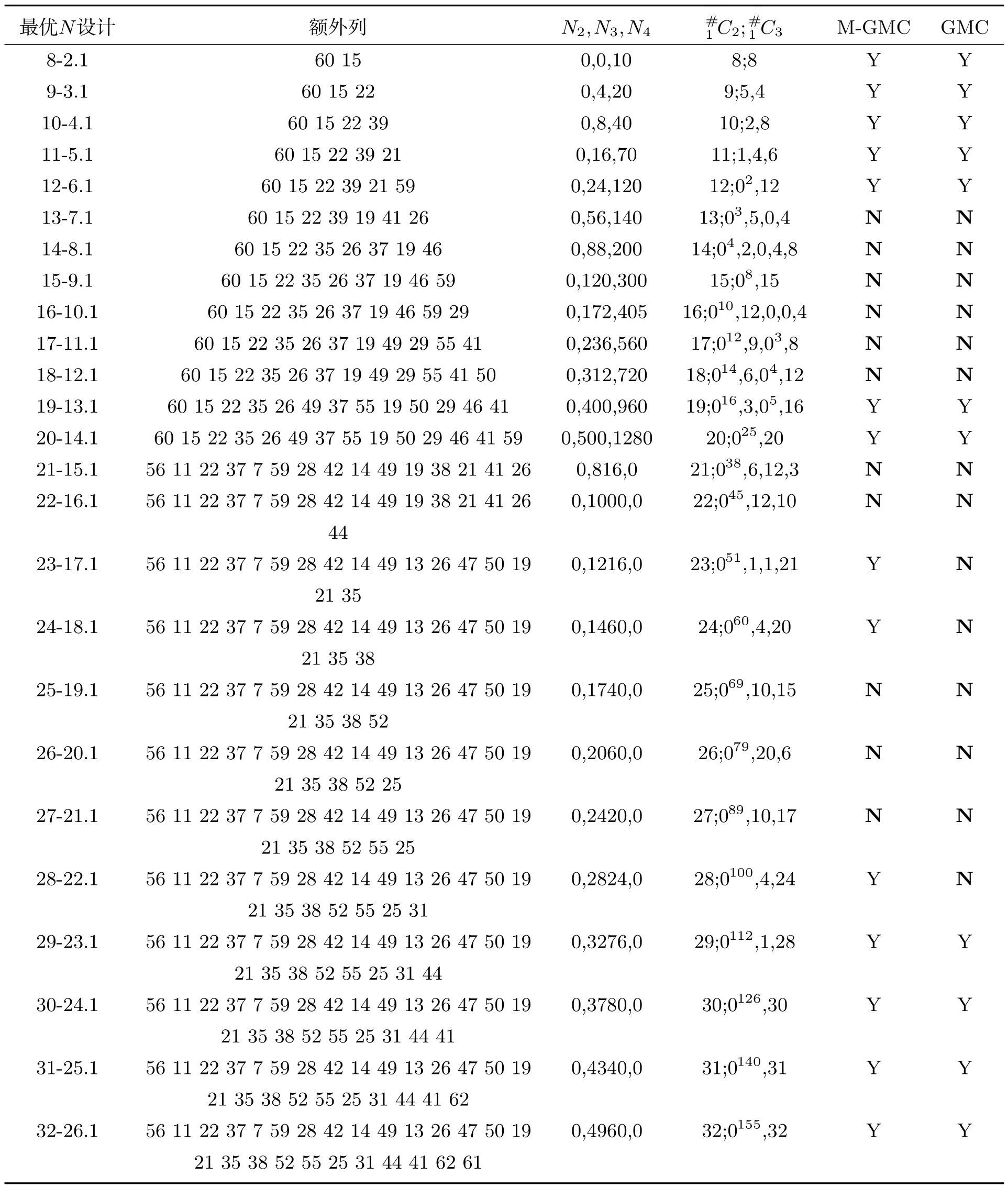
表6 64次试验的二水平设计

4 结论

本文主要研究2n－m正规设计中主效应与其它各阶因子之间混杂指标集的计算公式.首先通过线性回归模型的最小二乘估计的偏差得到了主效应与r阶因子交互效应之间的r阶别名矩阵Pr.在低阶效应的基础上, 提出基于主效应的别名效应数型及一般最小低阶混杂准则.分析了r阶别名矩阵Pr、混杂指标集以及别名效应数型之间的关系.利用别名矩阵Pr计算Nr更直观及简洁, 但当因子个数增加时, 别名矩阵的计算过程比较繁杂.在序列N = (N2,···,Nn)中元素N2最重要, 因此通过M-AENP函数中#1C(l)2给出N2的计算公式(定理3及定理4).定理5给出了通过AENP函数计算混杂指标集中的元素.最后一节通过表格列出试验次数为16、32及64次试验的二水平设计来比较混杂指标集、M-GMC准则、GMC准则下的最优设计.