传动主轴结构优化与疲劳寿命预测

贺宇,唐长亮,陈涛

(北京信息科技大学 现代测控技术教育部重点实验室,北京 100192)

0 引言

履带装甲车辆工作环境恶劣,行驶路况复杂,传动系统常在高幅值载荷与高温环境下工作。传动主轴作为传动系统中的关键部件,在复杂的循环应力与恶劣的工作环境下极易发生疲劳失效,一旦发生疲劳失效,将对整个传动系统造成严重破坏。

国内外学者对传动轴疲劳失效问题开展了大量研究。文献[1-2]对轴类零件疲劳失效的原因开展研究,发现工作载荷、结构参数、加工工艺、装配精度等都会影响零件疲劳寿命,且疲劳裂纹的萌发区均在零件结构形状突变处。文献[3-5]对传动轴的受载情况进行研究,根据实车测试载荷预测传动轴的疲劳寿命,为传动轴的结构优化与疲劳可靠性评估提供了参考依据。文献[6-8]仿真分析了不同结构参数对传动轴疲劳寿命的影响规律,提出了改进的传动轴抗疲劳结构。

目前对传动轴的结构优化与疲劳寿命预测研究尚未考虑温度效应。履带车辆传动系统输出扭矩大,传动构件温度常在100 ℃左右[9]。在起步与换挡时,主轴花键连接副会产生较大转速差,将产生局部摩擦高温。在微观研究方面,材料在高温环境下金相组织会发生改变[10-13];在宏观表现上,材料在高温环境下的力学性能不同于常温,温度对主轴材料疲劳性能亦有显著影响[14-16]。因此,研究履带车辆传动主轴疲劳寿命问题还需要考虑温度因素。

本文对某型履带装甲车辆传动主轴疲劳失效问题展开研究,根据传动主轴工作时的载荷特点与花键副传动摩擦生热计算模型,建立极限工况下传动主轴结构热耦合模型,结合解析法与响应面法对传动主轴结构进行优化,进一步研究结构参数与温度因素对传动主轴疲劳特性的影响,为传动主轴疲劳寿命预测与车辆传动系统的疲劳可靠性提供理论依据。

1 传动主轴结构-热力学计算模型

如图1所示,某型履带车辆工作时,发动机扭矩从传动主轴中间花键输入,在平稳行驶时,主轴工作扭矩通常在0～5 000 N·m左右,再由主轴两侧花键传递至两侧汇流行星排输出,传动主轴主要参数如表1所示。

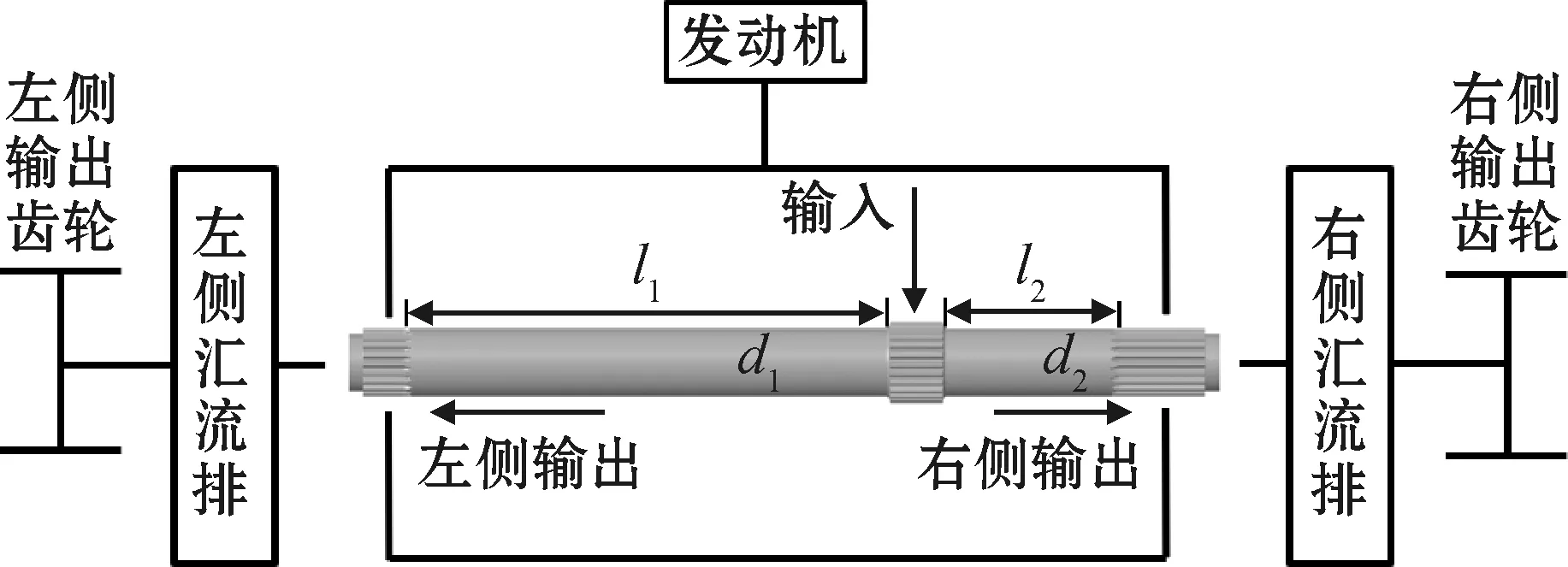
图1 传动主轴工作受载情况

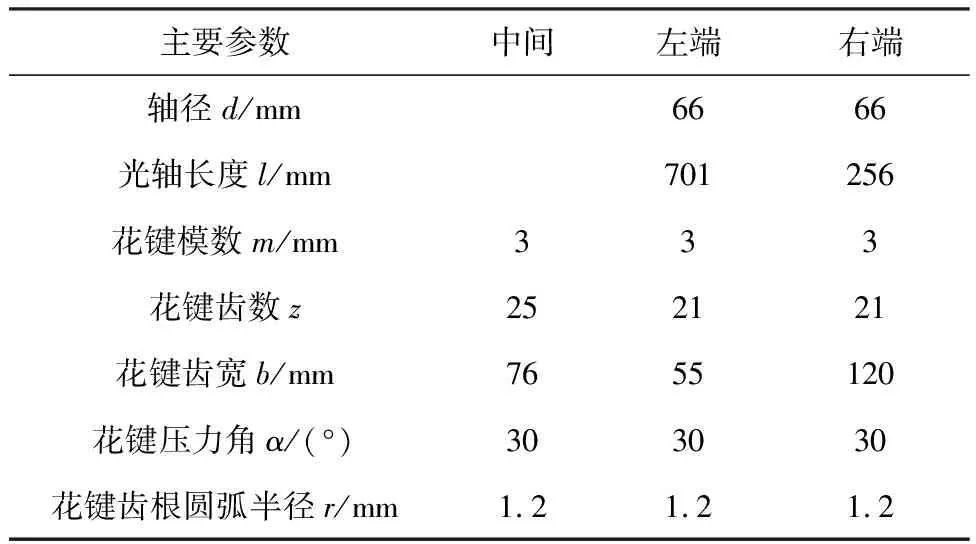
表1 渐开线花键主轴主要参数

传动主轴在复杂的工作条件下极易疲劳失效,其中70%疲劳损伤来自于起步与换挡工况[17],在此极限工况下,扭矩从中间花键输入时,主轴两端的花键尚未转动,近乎固定约束。此时传动主轴一次静不定力学模型如图2所示。

图2 主轴静不定力学模型

(1)

(2)

(3)

式中:i=1,2分别表示左端和右端;T1、T2分别为左、右端输出扭矩;M为输入扭矩;di为光轴直径;li为光轴长度;Gi为光轴材料室温下的剪切模量;kti为与局部温度有关的剪切模量影响系数;Wpi为扭转截面系数;σi为光轴面Mises应力;σri为花键齿根Mises应力。

式(3)中k为花键齿根应力集中系数[18],其表达式为

(4)

式中:r为花键齿根过渡圆弧半径;h为有效工作齿高;b为花键齿厚;d0为花键分度圆直径。

履带车辆在起步与换挡时,主轴花键副在传递大扭矩的同时还会有较大转速差,花键副齿面会产生大量摩擦热,其热流量计算模型[19]为

(5)

式中:λ为花键副材料热分配系数;T(t)为主轴花键副传递扭矩;μ为摩擦系数;ω(t)为主轴花键副转速差;z为花键齿数;S为花键副齿面接触面积。

主轴表面在变速箱内对流换热介质主要是空气和润滑油的混合物,可以简化为旋转圆盘的对流换热的计算,对流换热系数为

(6)

式中:k0为空气和润滑油混合物的热传导系数;r0为圆盘外表面半径;Nu为空气和润滑油混合物的努塞尔数,其表达式为

(7)

式中:Pr为空气和润滑油混合物的普朗特数;Re为空气和润滑油混合物的雷诺数,其表达式为Re=ωr0/v,其中ω为圆盘旋转速度,v为空气和润滑油混合物的运动粘度。

由式(1)～(3)可知,主轴受到的应力由工作扭矩、结构参数与工作温度决定,再由式(5)可知,工作扭矩与转速将会影响局部温度,从而改变主轴局部的剪切模量,使主轴受到的应力发生变化。

2 结构参数与温度效应对应力的影响

2.1 传动主轴扭转应力分析

在ANSYS中建立传动主轴有限元模型如图3所示,为模拟传动主轴花键副实际接触情况,建立渐开线内花键套模型与传动主轴外花键装配,由中间花键套输入扭矩,两端花键套固定约束,花键副接触类型为摩擦接触,摩擦系数为0.2,单元类型为Solid226,网格单元数量936 230个,经验证仿真计算结果趋于收敛,主轴模型材料为20Cr,其力学性能参数[20]如表2所示。

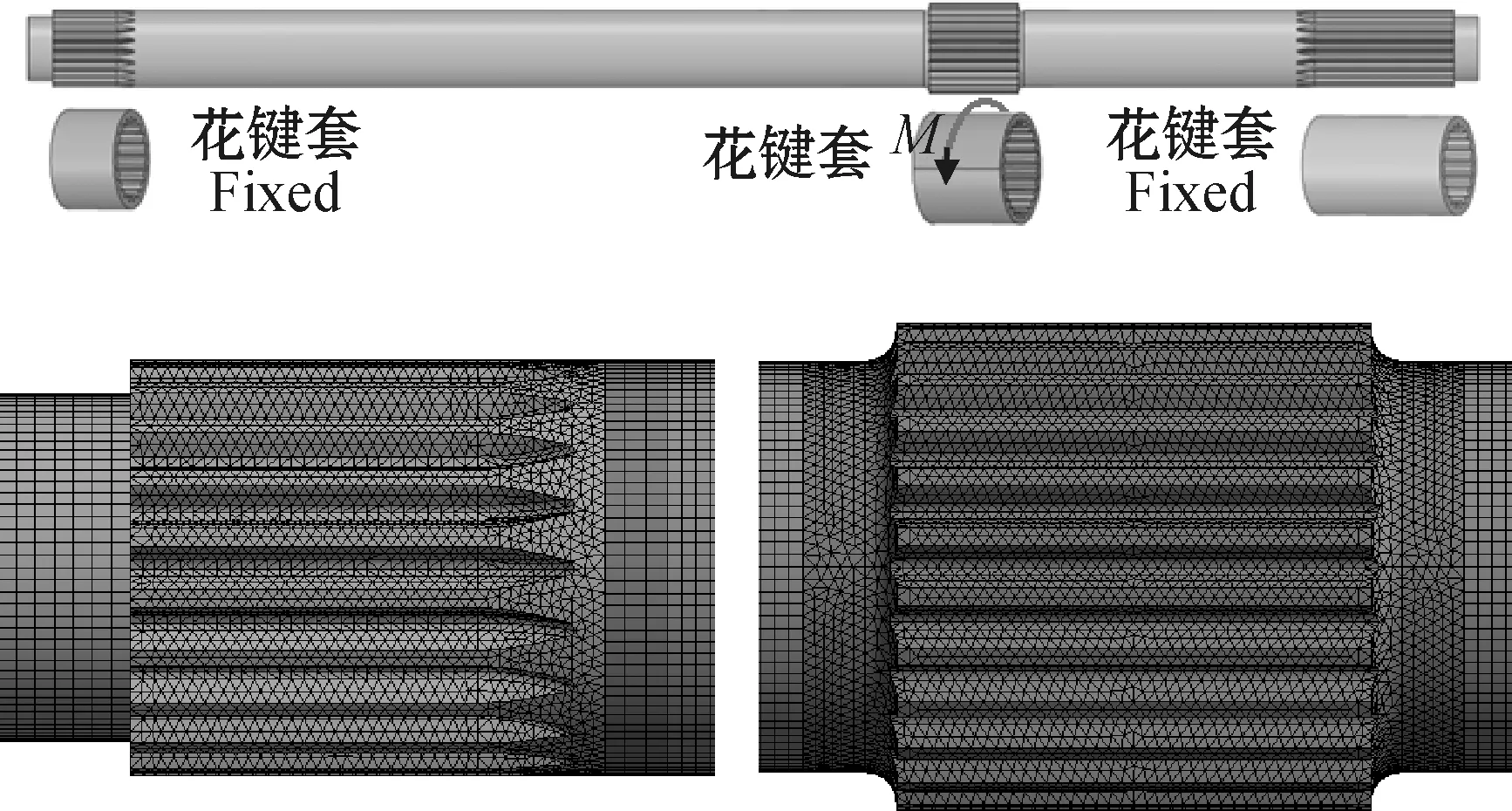
图3 传动主轴有限元模型

表2 主轴材料室温力学性能参数

由图4、5可知,此时传动主轴右端轴面受到的应力为左端的2.44倍,最大应力发生在右端花键齿根与退刀槽交界处,为左端花键齿根应力的2.58倍,最大应力处与主轴实际失效位置一致,对比解析解与有限元仿真结果,各区域误差不足5%,表明了有限元解的准确性。

图4 传动主轴应力云图

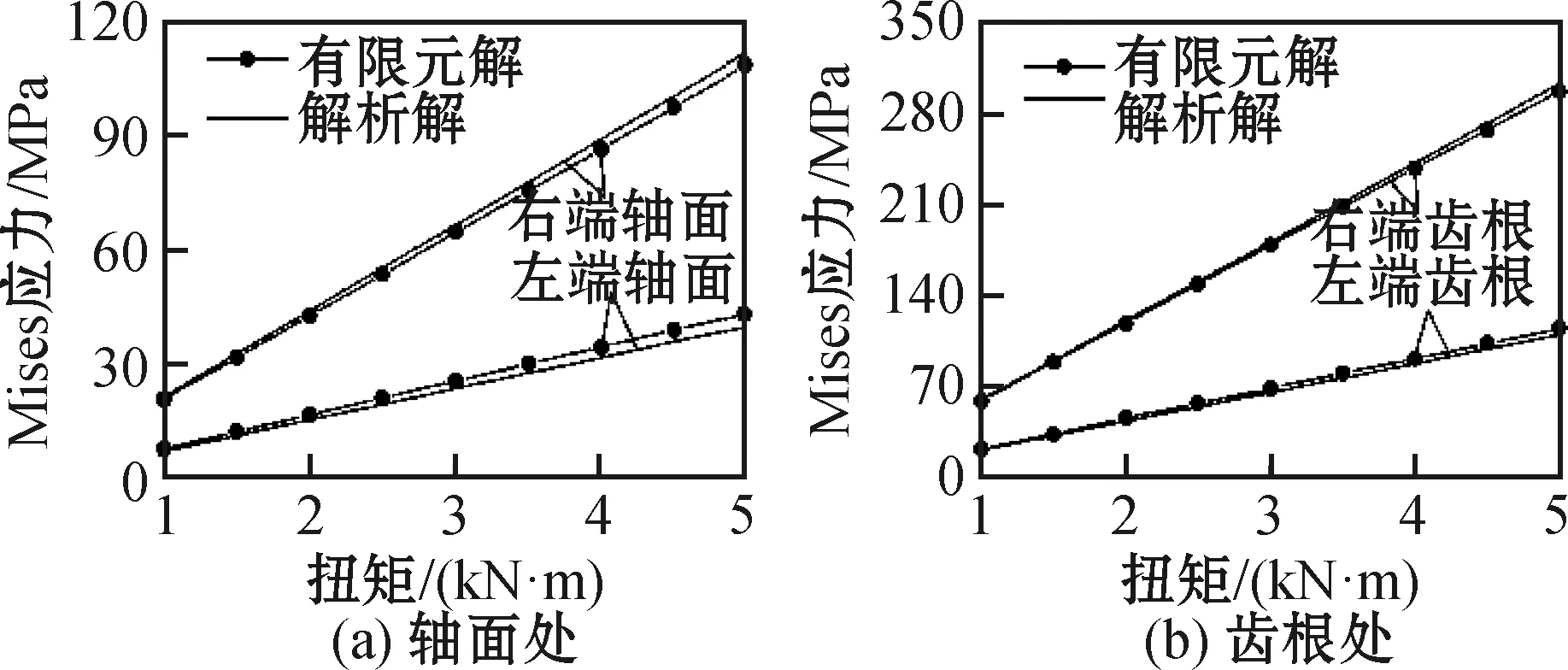
图5 传动主轴应力计算对比

2.2 传动主轴结构优化

由上面的主轴扭转应力分析可知,主轴工作时的危险区域为右端花键齿根处,影响右端花键应力分布的因素主要有输入载荷、结构参数与工作环境等,对该区域应力分布影响较大的结构参数有花键齿形、轴径与退刀槽曲率半径等,研究花键齿形、轴径与退刀槽曲率半径对应力的影响规律来改进主轴结构,使主轴质量更轻,受到应力更小。

2.2.1 齿廓修型

如图6所示,传动主轴将扭矩传递至右侧花键时,主轴的扭转变形γ沿轴向呈递减趋势,内花键套左侧局部区域与主轴外花键先发生接触,主轴外花键齿面在轴向受力不均匀,因此考虑对外花键齿廓进行修型[21],外花键齿廓改进方案如图7所示。

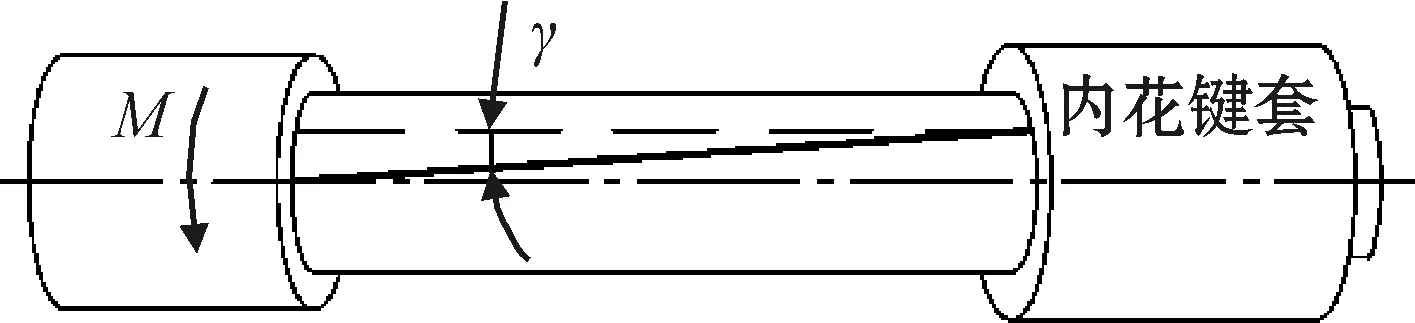
图6 主轴扭转变形示意图

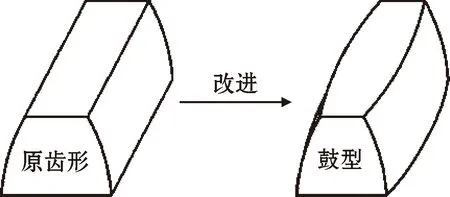
图7 外花键齿廓鼓型修型

图8为修型前后花键受载分布,可见,对主轴外花键齿廓进行修型后,齿面压力由集中在靠近输入端一侧,变成在花键齿面中间部位分布,接触压力更加均匀,压力由156.9 MPa下降至93.35 MPa,较修型前下降了40.5%;齿根最大Mises应力由119.83 MPa下降至110.37 MPa,较修型前下降了8.73%。

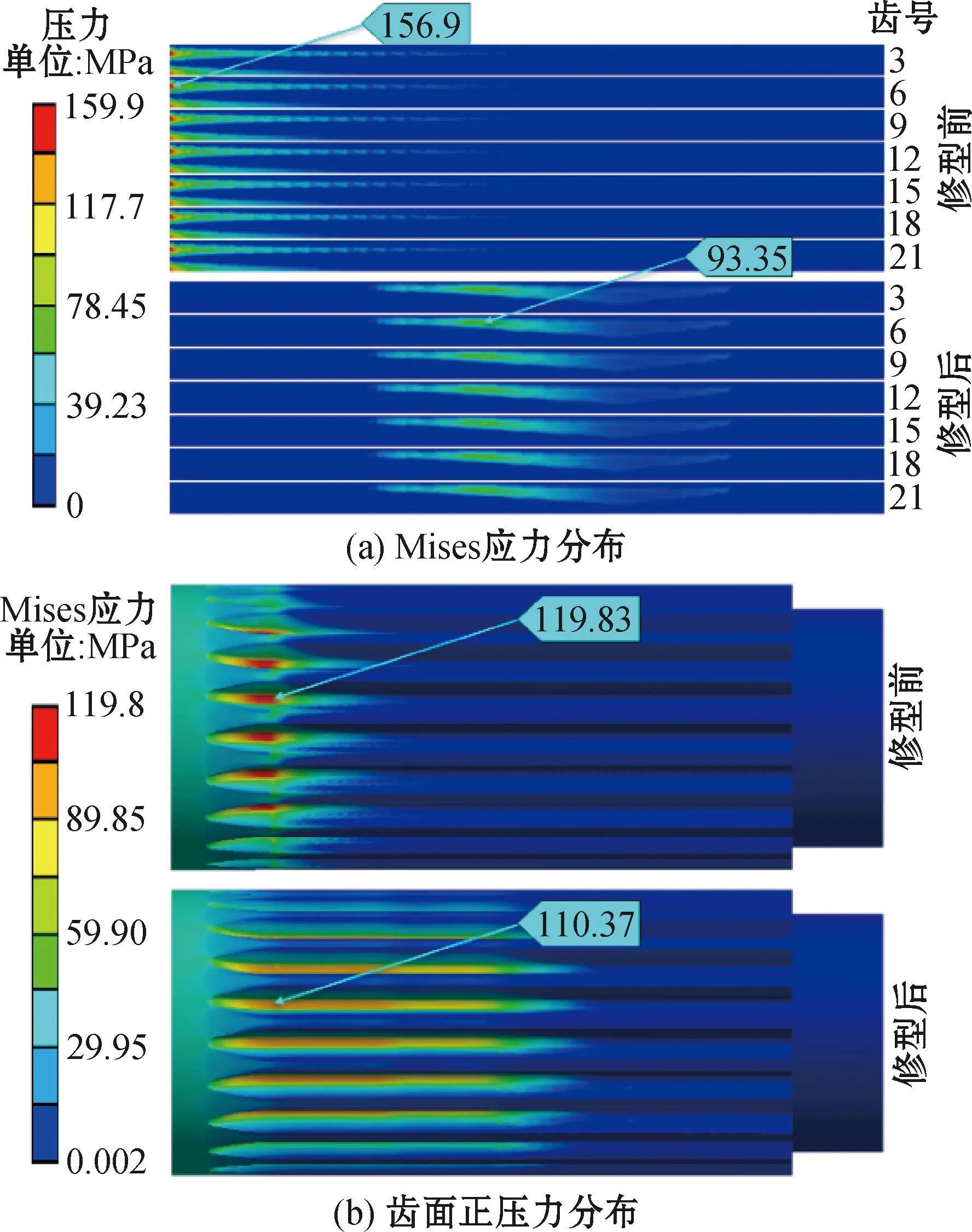
图8 修型前后花键受载分布

2.2.2 轴径与退刀槽优化

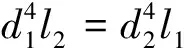
图10为主轴结构改进方法,根据静不定力学理论分析,轴径与退刀槽结构会极大影响花键齿根处的应力集中,改进轴径与退刀槽结构以减小主轴花键退刀槽处应力集中情况。由于静不定力学模型为简化模型,与主轴实际情况存在误差,实际最优轴径d2应该在51.3 mm的邻域范围内,取退刀槽半径R的优化区间为[0.5R,1.5R],在Workbench中建立传动轴优化模型进行二次优化,以右端轴径d2与退刀槽R为输入优化参数,在轴径d2∈[48,56]mm与R∈[15,45]mm区间内取100个样本点进行优化计算。

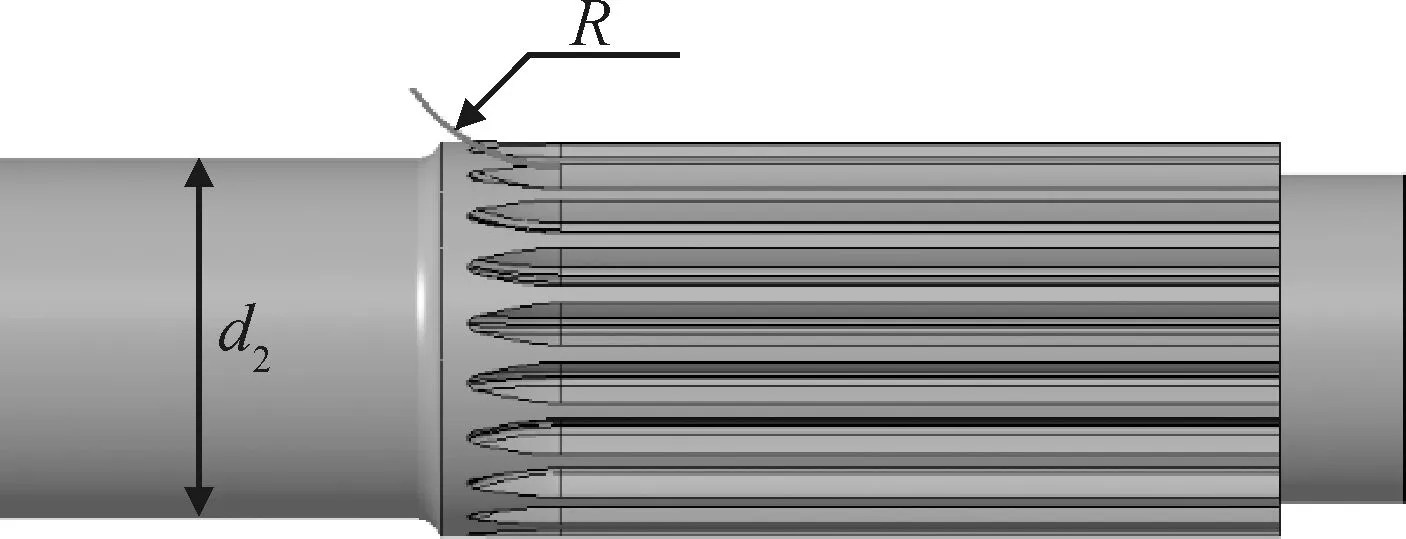
图10 传动主轴退刀槽改进结构

由图11可以看出,随着轴径d2增大,传动主轴的最大应力σmax与初始结构最大应力σ0之比呈现先减小后增大的趋势;当轴径d2=52 mm附近时,退刀槽曲率半径R越大,主轴最大应力越大,当轴径d2在[48,56]mm区间两端时,退刀槽曲率半径R越大,主轴最大应力越小。

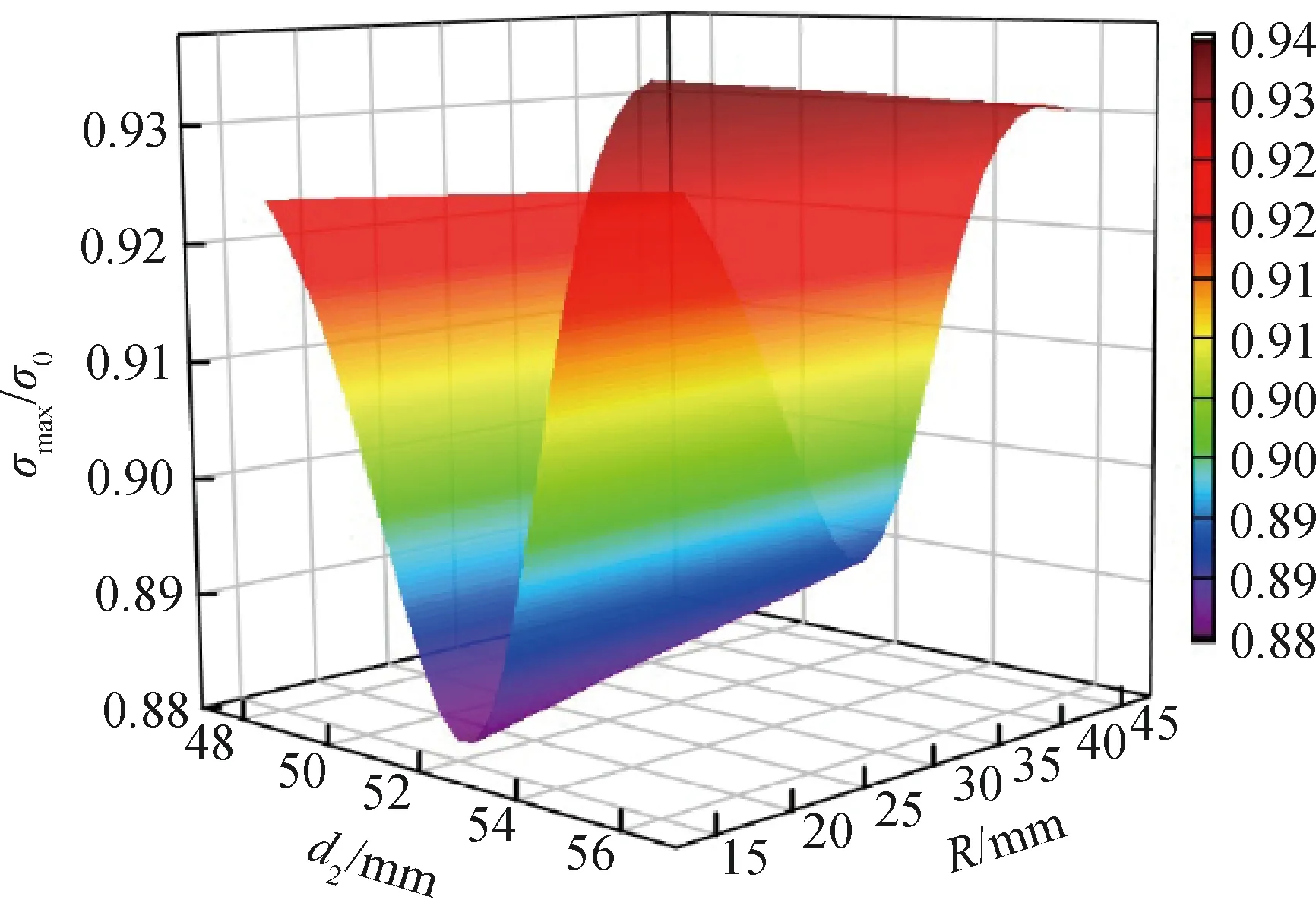
图11 传动主轴最大应力响应面

以式(8)为优化目标函数,在Workbench中以MOGA算法进行多目标优化计算,初始样本数量为5 000,每次迭代的采样数为200,最大迭代次数为200,计算得到一组最优解为d2=51.894 mm,R=15.318 mm。

(8)

式中:σmax为传动轴最大应力;m1为传动主轴改进后质量;m0为初始结构主轴质量。

将优化结果导入Workbench进行仿真计算,结果如图12、13所示。改进前主轴左右两端最大应力分别为46.52 MPa与119.83 MPa,应力主要集中在传动主轴右端;改进后主轴左右两端最大应力分别为86.25 MPa与88.1 MPa,左右两端受载分布更为均匀合理,最大应力总体水平下降了26.48%;主轴质量由34.387 kg下降至30.338 kg,较初始结构减轻了11.77%。

图12 优化后主轴应力分布云图

2.3 主轴结构-热应力分析

某型履带装甲车辆试验结果表明车辆换挡时间在0.5 s左右[22],在起步与换挡瞬间,传动主轴内外花键会有较大转速差,产生局部摩擦高温,在Workbench中对主轴进行瞬态热-结构耦合仿真,研究温度对传动主轴的应力分布的影响,主轴热边界条件如图13所示,主轴环境温度为100 ℃,齿面摩擦热流量与对流换热系数可由式(5)至(7)计算。

图13 主轴热边界条件

其中主轴20Cr材料热物理性能参数如表3所示,实车测试所得不同挡位传动主轴扭矩与转速数据如表4所示。

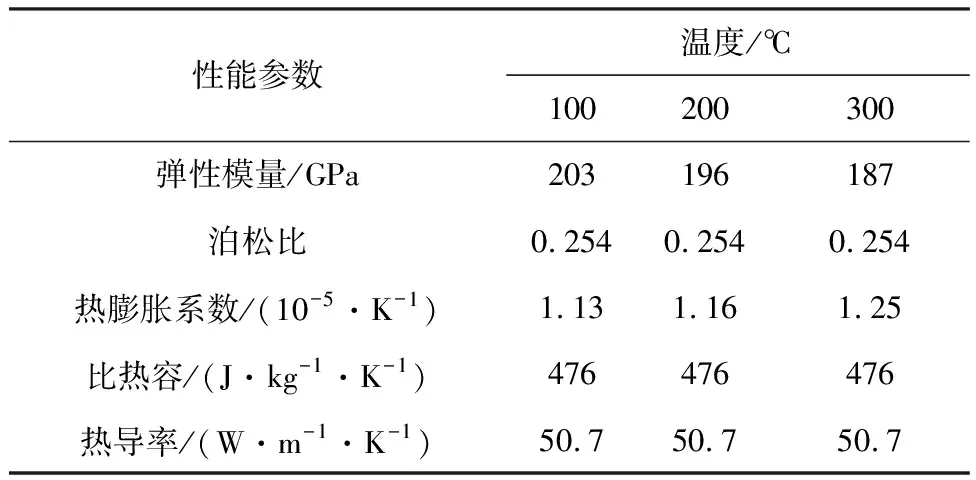
表3 20Cr热物理性能

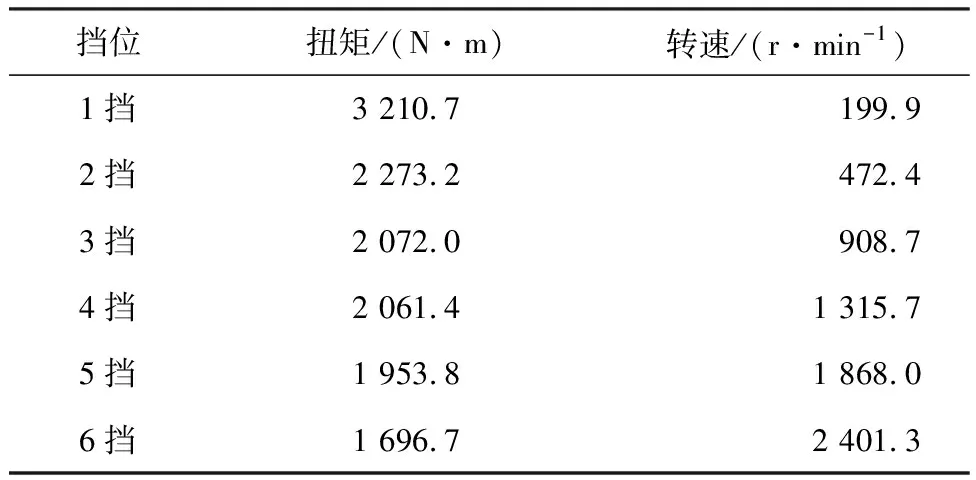
表4 各挡位主轴扭矩与转速

由图14可知,主轴大部分区域温度为100 ℃,这是受到了变速箱内的环境温度影响,而主轴花键齿上啮合面一侧会有局部高温,主要是由于花键副在起步与换挡时存在较大转速差,造成花键副啮合面上产生局部摩擦高温。

图14 二挡时传动主轴温度场分布

由图15可知,随着挡位上升,主轴扭矩降低,转速提高,最大应力逐渐降低。在考虑摩擦热后,主轴花键局部受摩擦高温的影响,最大应力较常温时存在明显的应力增量Δσ。

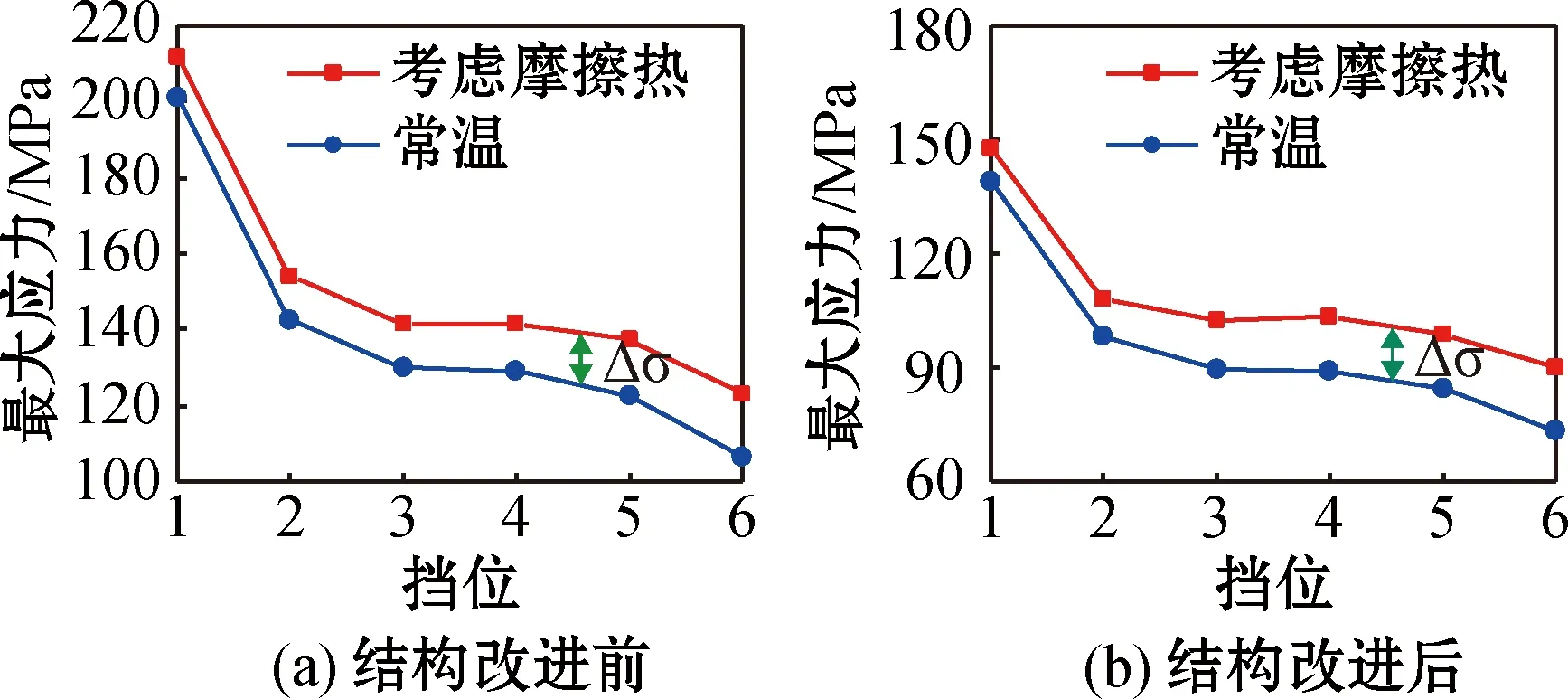
图15 考虑摩擦热与常温下的最大应力

图16为右端花键局部温度对应力的影响,主轴在结构改进前,6挡与1挡时的花键局部温度分别为228.43 ℃与176.11 ℃,温度差ΔT1为52.32 ℃;主轴在结构改进后,6挡与1挡时的花键局部温度分别为189.07 ℃与152.79 ℃,温度差ΔT2为36.28 ℃。主轴结构改进后,最大温度较改进前下降了39.36 ℃,温度差ΔT较改进前下降了16.05 ℃。

花键局部温度越高,主轴最大应力的应力增量Δσ越大。应力增量Δσ随局部温度上升而增大,其应力增量Δσ与局部温度呈现线性关系;在低挡位时,主轴局部温度较小,应力增量Δσ在10 MPa左右;在高挡位时,主轴局部温度较大,应力增量Δσ超过了16 MPa。

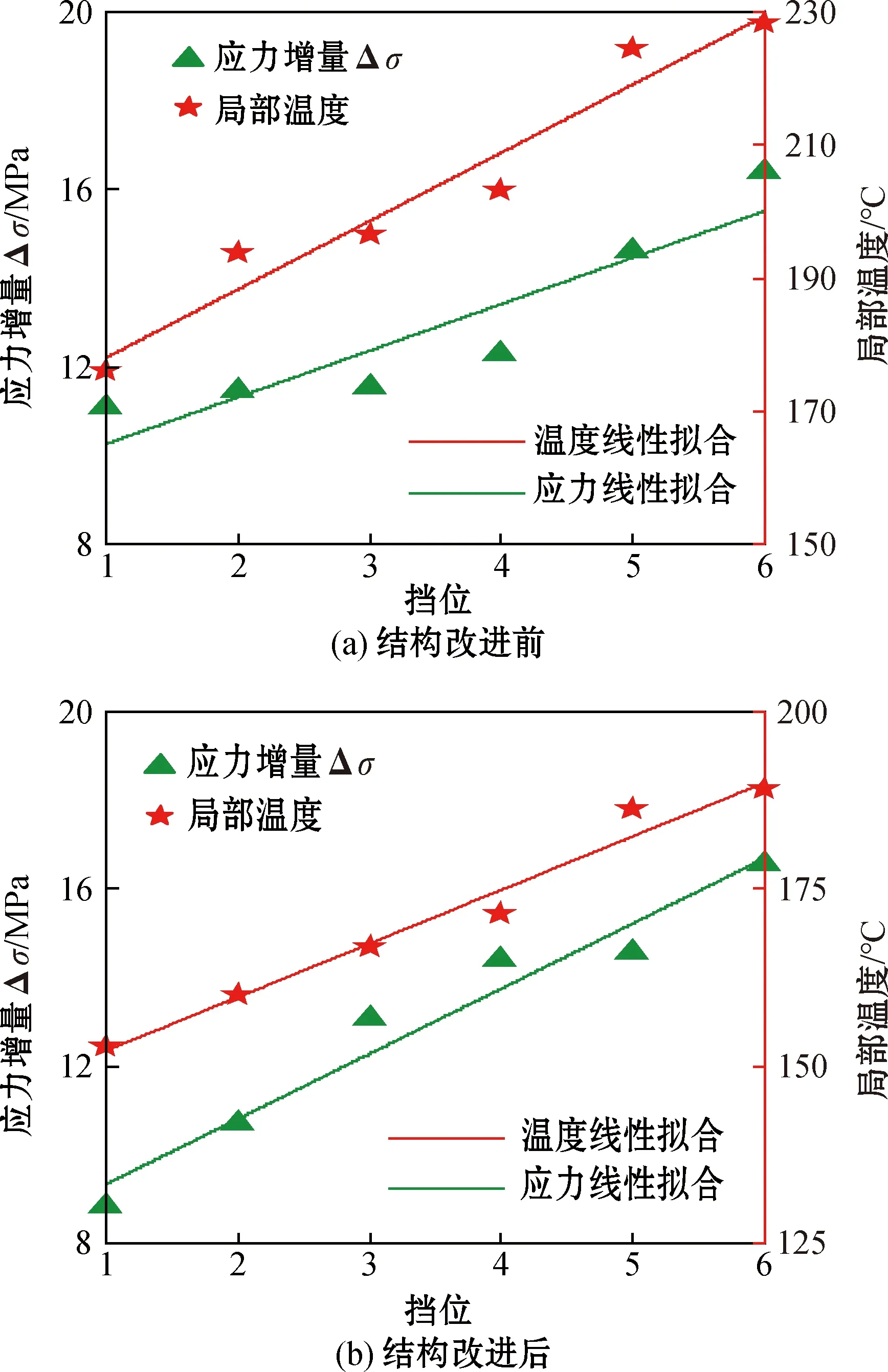
图16 右端花键局部温度对应力的影响

3 疲劳寿命分析及预测

在循环应力幅的作用下,主轴极易发生疲劳失效,主轴起步与换挡时的扭矩载荷相当于非对称循环载荷,不同挡位输入载荷形式如图17所示。

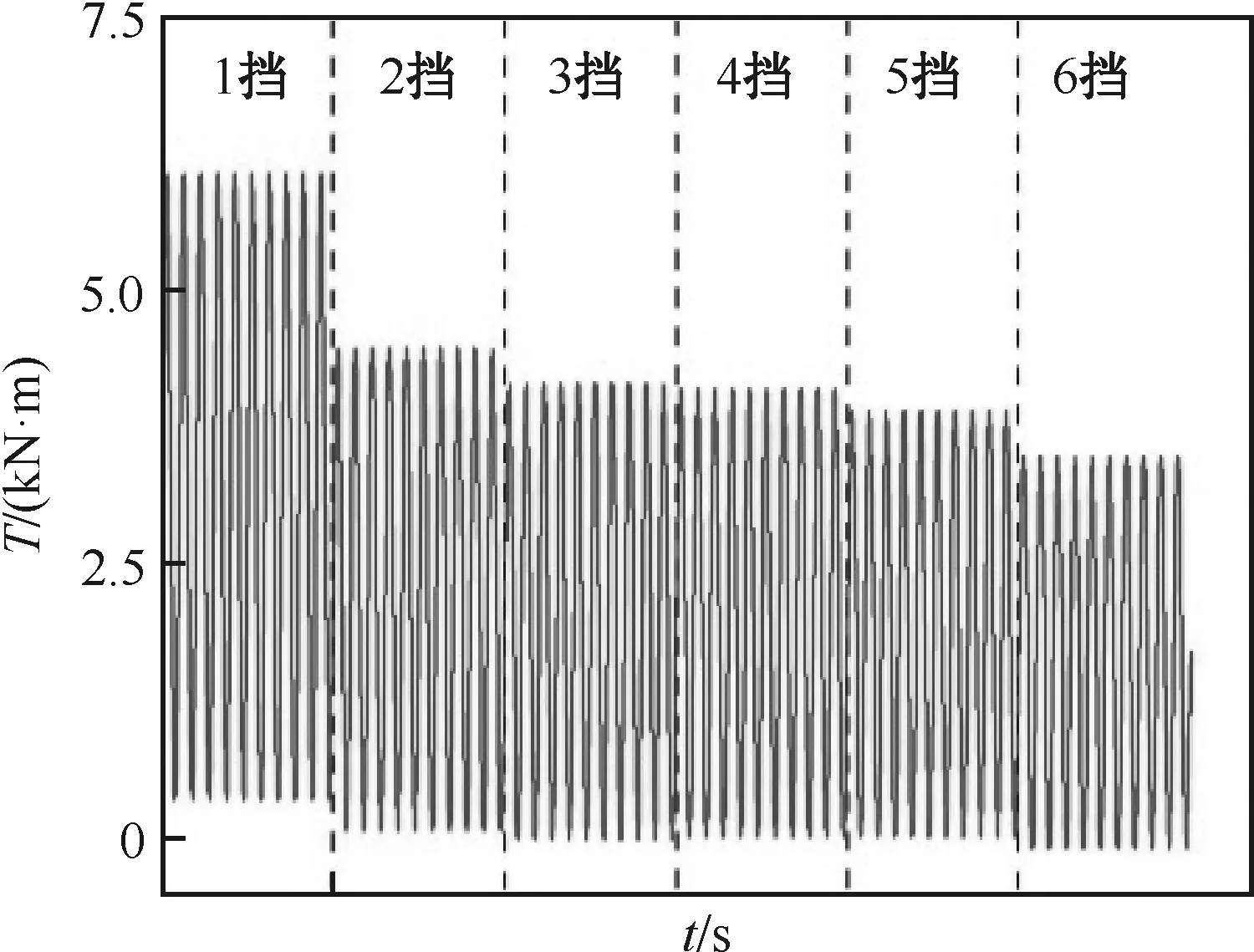
图17 不同挡位输入载荷

根据分析可知最大应力发生在右端花键齿根处,由Goodman理论修正平均应力影响,基于Miner疲劳损伤理论计算主轴危险处疲劳寿命,主轴材料20Cr的SN曲线拟合式为

lgNf=45.783 8-16.102lgσ

(9)

式中:Nf为疲劳寿命;σ为循环应力幅。

由图18可以看出,主轴在高挡位时的疲劳寿命远大于低挡位时的疲劳寿命,这是由于挡位越高主轴花键处传递扭矩越小,危险区应力越低,对主轴损伤极小。

对于优化前的原始结构主轴,在高挡位如5挡时,主轴在常温时的疲劳寿命Na5为3.14×106次,在考虑摩擦温度效应后的寿命Nat5为4.01×105次,局部高温致使主轴寿命仅为常温时的12.77%;在低挡位如2挡时,主轴在常温的疲劳寿命Na2为3.13×105次,在考虑摩擦温度效应后的寿命Nat2为7.39×104次,局部高温致使主轴寿命仅为常温时的23.61%。在高挡位时,温度对疲劳寿命的影响比低挡位时更大。

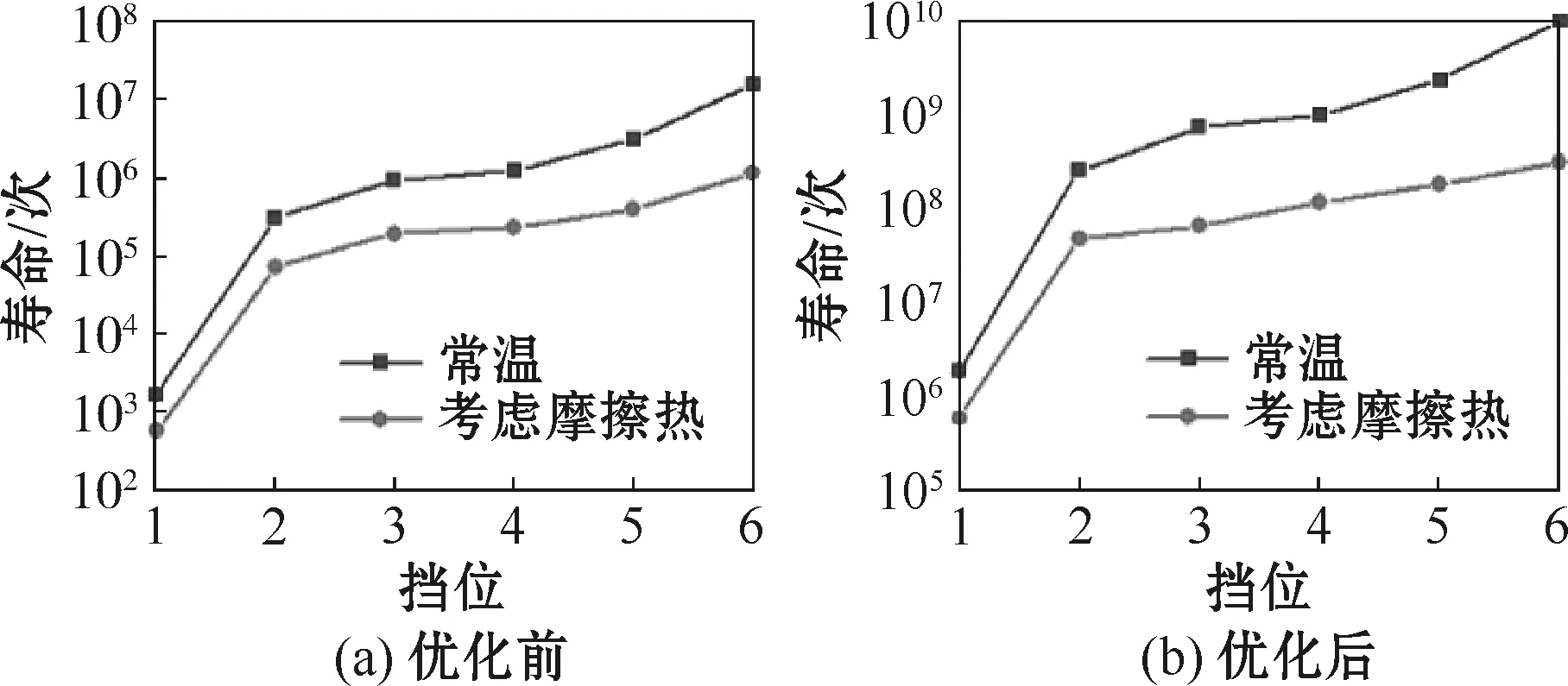
图18 各挡位下结构与温度对寿命的影响

对于结构优化后的主轴,在高挡位如5挡时,主轴在常温时的寿命Nb5为2.37×109次,考虑摩擦温度效应后的寿命Nbt5为1.85×108次,局部高温致使优化后主轴寿命Nbt5仅为常温时寿命Nb5的7.81%;在低挡位如2挡时,主轴在常温时的寿命Nb2为2.62×108次,考虑摩擦温度效应后的寿命Nbt2为4.90×107次,局部高温致使改进后主轴寿命仅为常温时的18.71%。

4 结束语

针对履带车辆传动主轴疲劳失效问题,建立极限工况下传动主轴结构-热力学计算模型,结合解析法和响应面法对主轴结构进行优化,研究了结构参数与温度效应对主轴应力分布与疲劳寿命的影响规律。研究结果表明,主轴优化后左右端应力趋于一致,最大应力降低了26.48%,质量下降了11.77%,考虑温度效应后,主轴在2挡工作时的疲劳寿命仅为常温时的18.71%,为传动主轴疲劳寿命预测与车辆传动系统的疲劳可靠性评估提供了理论依据。